научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#12 декабрь 2005
Г. Б. Евгенев, д-р техн. наук, МГТУ им. Н. Э. Баумана
Модели вместо алгоритмов.
Смена парадигмы разработки прикладных систем
Описана история развития информационных технологий. Приведена системологическая классификация уровней и моделей знаний. Особое внимание уделено уровню структурированных порождающих систем: представлению и использованию математических и экспертных знаний. Дано введение в мультиагентную методологию компьютеризации инженерных знаний.
Известная формула Н. Вирта: "алгоритмы + структура данных = программы" свидетельствует о том, что в недрах программных средств существуют два начала, две противоположности, находящиеся, как водится, в диалектическом единстве и борьбе. Одно начало — императивное, командное, алгоритмическое, а другое — декларативное, непроцедурное, основанное на моделях. Заря информатики была ознаменована полным, безраздельным, империалистическим торжеством алгоритмического начала. Это начало, чуждое стилю человеческого мышления, которое до того практически не использовало алгоритмическую форму для изложения своих результатов, привело к возникновению новой профессии — программистов. Программисты надолго оттеснили от компьютеров непрофессионалов.
Только появление персональных компьютеров с их простым и доступным графическим интерфейсом позволило, наконец, широким кругам непрофессионалов сесть за монитор компьютера. Однако они по-прежнему не допущены в "святая святых" храма информатики — в цех, где создаются программные средства.
Человечество вступает в век информатики. В недалеком будущем каждый "белый воротничок" должен будет иметь свое персональное рабочее место, оснащенное не только универсальными программными средствами, такими как текстовый или графический редактор, но и специализированной системой, наполненной его личными знаниями и опытом. Программистам никогда не справится с этой грандиозной задачей. Им придется допустить непрофессионалов в "святая святых" своего храма. Но для этого нужно будет сменить алгоритмы на модели и создать необходимые программно-методические средства.
Краткая история борьбы моделей с алгоритмами
Модель и алгоритм представляют собой фундаментальные понятия математики и информатики. Под моделью понимают определенное множество абстрактных объектов или несколько множеств абстрактных объектов разной природы, различающихся условно приписываемыми им именами, в совокупности с заданной системой отношений между элементами этих множеств. Алгоритм — это точное предписание последовательности действий, необходимых для получения искомого результата. В настоящее время модель в большинстве случаев используется лишь для формального описания объекта вычислений, определяя ЧТО надо вычислить. Алгоритм как основа вычислительного процесса определяет, КАК нужно вычислять.
Абсолютно ясно, что без установления того, что надо определить, процесс вычисления смысла не имеет. Поэтому без модели не обойтись. Вопрос о роли и месте алгоритма не так прост, как кажется на первый взгляд, и представляет собой наибольший интерес. Без алгоритма, конечно, тоже не обойтись, однако, используя методологию искусственного интеллекта, его можно исключить из спецификации задачи.
История развития информационных технологий свидетельствует о том, что модели медленно, но неуклонно теснят алгоритмы.
На первом этапе развития информационных технологий компьютеры использовались для решения сложных вычислительных задач, связанных с освоением космоса и энергии атомного ядра. Программы включали операторы управления и обработки данных, а также своего рода эмбрион модели — раздел данных, содержавший неструктурированное описание множества переменных (рис. 1, а).

Рис. 1. Этапы развития программных средств
На втором этапе компьютеры стали применяться для автоматизации менеджмента и обработки больших объемов информации. Возникла концепция баз данных, теоретическую основу которой составили математические модели структур данных. Так модели, формируемые с помощью языков описания данных, впервые вошли в практику программирования (рис. 1, б).
Побудительным импульсом для начала третьего этапа послужили работы по созданию интеллектуальных роботов. На этом этапе возникла концепция баз знаний, основанная на теории искусственного интеллекта. Появились оболочки экспертных систем, использующие различные модели знаний (рис. 1, в), необходимые для принятия решений. Модели расширили свой плацдарм, перешагнув из области пассивных в область активных информационных ресурсов. Что касается алгоритмов, то они стали превращаться в инвариантные программные средства — операционные среды, обеспечивающие решение задач, формулируемых человеком на языке моделей.
В начале третьего этапа имели место ошибочные и вредные для дела распри между специалистами в использовании различных видов моделей данных и знаний. В настоящее время созрело понимание общности подхода, понимание того, что различные модели не конкурируют, а отражают разные грани единого целого — интегрированной модели мира сего.
Таким образом, если на первом этапе раздел данных можно рассматривать как эмбрион модели в алгоритмическом теле, то интеллектуальный решатель на третьем этапе представляет собой рудимент алгоритма в теле моделей.
"Таблица Менделеева" для моделей
Каковы же эти грани единого целого и какие модели необходимы для их представления? Любая модель включает два основных компонента: множество объектов и множество отношений:
![]()
где М
— модель; А — носитель модели; ![]() — i-е
отношение (i = 1, ..., n).
Совокупность этих отношений формирует сигнатуру модели. Если использовать в
качестве критерия классификации тип носителя, то получается традиционное
разделение науки и техники на дисциплины и специальности, каждая из которых
занимается определенным типом элементов (физика, химия, машиностроение,
электроника и т. п.). Совершенно иную классификацию систем дает применение в
качестве критерия типа отношений. Наукой, изучающей системы в этом разрезе,
является системология. С точки зрения системологии [1] иерархия классов
определяется эпистемологическими уровнями, т. е. уровнями знаний относительно
рассматриваемых явлений (табл. 1).
— i-е
отношение (i = 1, ..., n).
Совокупность этих отношений формирует сигнатуру модели. Если использовать в
качестве критерия классификации тип носителя, то получается традиционное
разделение науки и техники на дисциплины и специальности, каждая из которых
занимается определенным типом элементов (физика, химия, машиностроение,
электроника и т. п.). Совершенно иную классификацию систем дает применение в
качестве критерия типа отношений. Наукой, изучающей системы в этом разрезе,
является системология. С точки зрения системологии [1] иерархия классов
определяется эпистемологическими уровнями, т. е. уровнями знаний относительно
рассматриваемых явлений (табл. 1).
Самый нижний уровень в этой иерархии, обозначаемый как уровень 0, — это система, различаемая исследователем как таковая. На этом уровне система определяется через множество свойств и носит название исходная система. Иными словами, на уровне 0 рассматриваются свойства исследуемой или проектируемой системы.
На более высоких эпистемологических уровнях системы отличаются друг от друга уровнем знаний относительно переменных соответствующей исходной системы. В системах более высокого уровня используются все знания систем более низких уровней и, кроме того, содержатся дополнительные знания, недоступные низшим уровням.
После того, как исходная система дополнена данными, т. е. фактическими состояниями переменных, рассматривают новую систему (исходную систему с данными) как определенную на эпистемологическом уровне 1. Системы этого уровня называются системами данных.
Уровень 2 представляет собой уровень базы знаний генерации значений переменных, определяющих свойства исходной системы. На этом уровне задаются функциональные связи переменных, в число которых входят переменные, определяемые соответствующей исходной системой и, возможно, некоторые дополнительные. Правило преобразования базы знаний на этом уровне обычно представляет собой однозначную функцию, присваивающую каждому элементу множества переменных, рассматриваемых в этом правиле в качестве выходного, единственное значение из множества допустимых.
Таблица 1
Уровни представления знаний и их модели
|
№ уровня |
Уровень знаний |
Наименование модели |
Модель |
Носитель модели |
Сигнатура модели |
|
0 |
Исходная система |
Модель данных объекта (понятие и его интенсионал) |
В = <А; Rk> |
Словарь свойств объектов (множество атрибутов) А = {a1, a2, ..., ak} |
Схема отношения (содержание понятия) Rk Rk = {ai1, ai2,…, aik}. Ключ отношения Kp |
|
1 |
Система данных |
Множество экземпляров объектов (выборка из объема понятия) |
E= =<D1, D2,…, Dk; rk> |
Домены атрибутов (допустимые множества значений атрибутов) Di = dom(ai) |
Отношение со схемой Rk rk Множество кортежей (денотатов понятия) rk=( |
|
2 |
Порождающая система |
Метод объекта: |
P= =<V1, V2,…, Vr; F> |
Свойства объекта и переменные метода |
Функциональное отображение F |
|
1. Математическая негеометрическая модель |
|
Числовые константы и переменные, функции, математические и логические отношения, операторы и операции |
Системы уравнений и неравенств |
||
|
2. Геометрическая модель |
|
Точки, линии, поверхности, тела |
Объединения, пересечения, вычитания преобразования, расчеты параметров |
||
|
3. Модель экспертных знаний (продукционное правило) |
|
Числовые и нечисловые переменные: входные Vi | u(i) = 0, выходные Vi | u(i) = 1, где u(i) — определитель вход-выход |
Отображение входных переменных в выходные |
||
|
3 |
Структурированная система: исходная |
Мультиагентная система (сеть агентов) |
SB = <B, А; C> |
Объекты и их свойства B = {b1, b2,…, bl}, A = {a1, a2,…, an} |
Семантическая сеть объектов C |
|
данных |
База данных (реляционная) |
SD = <B, G; J> |
Объекты и мощность отношений между ними B = {b1, b2,…, bl}, G{O, P, Z, N} |
Структура базы данных J |
|
|
порождающая |
База знаний (метод объекта) |
SP = <F, V; K> |
Правила и переменные модели F = {f1, f2,…, fl}, V = (v1, v2,…, vn) |
Семантическая сеть правил K |
|
|
4 |
Метасистема |
Модель метасистемы (И-ИЛИ граф) |
MB = <B, M; L> |
Объекты и типы связей между ними B = {b1, b2,…, bl}, M = {AND, OR} |
И-ИЛИ граф L |
Поскольку задачей генерации свойств является реализация процесса, при котором состояния переменных могут порождаться по множеству параметров при определенных начальных или граничных условиях, системы уровня 2 называются порождающими системами (generative system).
На эпистемологическом уровне 3 системы, определенные как порождающие или системы более низкого уровня, называются подсистемами общей системы. Эти подсистемы могут соединяться в том смысле, что они имеют некоторые общие переменные. Системы этого уровня называются структурированными системами (structured system).
На эпистемологических уровнях 4 и выше системы состоят из набора систем, определенных на уровне 1, 2 или 3, и некоторой метахарактеристики (правила, отношения, процедуры), описывающей замены в системах более низкого уровня. Это — уровни, необходимые для формирования концептуальных И-ИЛИ графов.
Лестница моделей к вершинам знаний
Модели первых двух уровней достаточно хорошо изучены в теории реляционных баз данных. Исходная система предназначается для описания некоторого объекта или эквивалентного ему понятия. Носителем модели являются атрибуты различных типов, неструктурированное множество которых с описанием идентификаторов, типов и наименований на языке деловой прозы образуют словарь. Сигнатурой модели уровня 0 является схема реляционного отношения, определяющего объект или содержание понятия.
Система данных представляет собой некоторое множество экземпляров объекта или выборку из объема понятия, определяемого исходной системой. Носителем модели уровня 1 являются домены атрибутов, а сигнатуру представляет реляционное отношение со схемой, описанной на уровне 0.
Порождающая система связана с методом объекта, определяющим его поведение. В зависимости от типа моделей можно выделить математические модели негеометрические, геометрические и экспертные. Носителем негеометрической модели являются числовые константы и переменные, функции, математические и логические операторы, отношения и операции. Сигнатуру таких моделей образуют системы уравнений и неравенств. Носитель геометрической модели формируется нульмерными, одномерными, двухмерными и трехмерными элементами, а сигнатура строится на базе теоретико-множественных операций, а также геометрических преобразований и операторов расчетов длин, площадей, объемов, центров масс, моментов инерции и т. п.
Экспертные модели отличаются от математических тем, что в качестве носителя помимо числовых могут появляться и нечисловые переменные. Сигнатура таких моделей строится обычно на базе продукционных правил, на основании которых при определенных условиях входные переменные отображаются в выходные.
Возможны различные подходы к построению программно-методических средств, реализующих описанную выше иерархию моделей знаний. Можно попытаться связать с помощью интерфейсных модулей созданные различными разработчиками СУБД пакеты расчетных программ, геометрический моделлер, оболочку экспертной системы, средства генерации прикладных интерфейсов. Многолетний опыт показывает, что это путь в никуда. Подобное лоскутное одеяло нежизнеспособно.
В СПРУТ-технологии создание иерархии моделей знаний ведется на единой программно-методической основе (рис. 2). Ядром системы компьютеризации знаний является монитор СПРУТ, который служит как для создания специализированных подсистем формирования знаний различного уровня, так и для решения задач на базе сформированных моделей.

Рис. 2. Иерархия моделей в интегрированной среде СПРУТ:
СИС — структурированная исходная система; ССД — структурированная система данных; СПС — структурированная порождающая система; ММС — мультиагентная метасистема
Уровень порождающих систем является основной ареной борьбы моделей с алгоритмами. До недавнего времени казалось, что у прикладного специалиста нет другой возможности, кроме как написать нужную ему модель, т. е. систему уравнений и неравенств, и искать в вычислительной математике подходящий алгоритм решения. Не найдя такового — подбирать аппроксимацию своей модели другой, для которой алгоритм есть.
Интеллектуальный решатель математических задач UniCalc®, разработанный под руководством А. С. Нариньяни на базе предложенной им методологии недоопредеденных вычислений, позволяет упразднить алгоритмы в своей области [2]. При этом форма представления знаний практически не отличается от общепринятой математической, как это можно видеть из табл. 2.
Таблица 2
Математические негеометрические модели
|
Наименование модели |
Представление модели на входном языке UniCalc® |
|
Система линейных уравнений |
1,1161*x1 + 0,1254*x2 + 0,1397*x3 + 0,1490*x4 = 1,5471; 0,1582*x1 + 1,1675*x2 + 0,1768*x3 + 0,1871*x4 = 1,6471; 0,1968*x1 + 0,2071*x2 + 1,2168*x3 + 0,2271*x4 = 1,7471; 0,2368*x1 + 0,2471*x2 + 0,2568*x3 + 1,2671*x4 = 1,8471; |
|
Система нелинейных уравнений, неравенств и логических выражений |
x3 + 10*x = yx – 2k; k*x + 7,7*y = 2,4; (k - 1)y + 1 < 10; ln(y + 2*x +12) < k + 5 or y>k2 → x < 0 and y<1; x <0 → k> 3; |
|
Система дифференциальных уравнений |
Dx / Dt = v; Dv/ Dt = -x + am*(1,0 - x^2)*y; am : = 0.5; x : = 1;v : = 0; t : = [0, 6.0]; |
|
Задача оптимизации |
f(x, y) : = x^2 + y^2 + x*y; (*Целевая функция*) fx(x, у) : = 2*x + у; fx(x, у) = 0; (* Частная производная по х *) fy(x, у) : = 2*у + х; fy(x, у) =0; (* Частная производная по у *) fmin = f(x, у); (* Экстремальное значение *) |
В СПРУТ - технологии геометрические знания представляются в форме подпрограмм на геометрическом языке. Формальные переменные этих подпрограмм соответствуют размерной информации чертежа объекта, которая формируется в результате работы баз знаний, осуществляющих параметрический синтез. В табл. 3 приведен пример представления геометрических знаний применительно к деталям типа тел вращения. Размерная информация передается посредством множеств SET, в которые могут заноситься как числовые данные, так и геометрические объекты (точки, прямые, окружности, контуры). Эти множества выполняют роль глобальных переменных. Во многих случаях геометрические знания представляются в виде параметризованных контуров. В приведенном примере — это контур образующей поверхности вращения. Для призматических поверхностей — контур направляющей, для кинематических — контуры образующих и направляющих.
Таблица 3
Геометрические модели
|
Элементы |
Геометрические значеня |
Геомтрические модели |
|
|
Двухмерная |
Трехмерная |
||
|
Поверхности тела вращения |
Контур образующей детали Da = SET[1,1]; La = SET[1,2]; Ca = SET[1,3]; P1 = 0,0; L1 = Ly, M0; L2 = X(Ca), Y(Da/2), A45; L3 = Lx, M(Da/2); L4 = X(La - Ca), Y(Da/2), A45; L5 =Ly, M(-La); L6 = Lx, M0; P2 = L5,L6 K1 = P1, L1, L2, L3, L4, L5, P2 TOSET(2) = K1 |
! Поверхность вращения P1 = 0,0 P3 = X(0,001), Y0; C1 = X0, Y0, R(0,001) K2 = P3, C1, P3 K1 = SET[2], P1, P1, A90 MATR 1 = ROT, X A90 CC 1 = K1 CC 2 = K2 SS 1 = RADIAL, BASES = CC2 DRIVES = CC 1, STEP 0.0002, 0,5 AS i = SS 1 |
! Тело вращения P3=0,(SET[1,1] / 2-SET[1,3]) P3D 1 = 0,0,0 P3D 2 = SET[1,1],0,0 SOLID(j)=ROT, P3D1, P3D2 Set[2], P3, M(0.5) |
Подпрограммы построения поверхностных и твердотельных геометрических моделей инвариантны для каждого класса объектов, поскольку необходимые для их выполнения контуры передаются через множества.
В СПРУТ - технологии имеются несколько способов создания геометрических подпрограмм:
· в обычном режиме написания и отладки программ с помощью монитора среды;
· посредством параметризации контуров из существующих геометрических баз данных, в том числе созданных с помощью средств, отличных от СПРУТ и использующих стандарт DXF;
· в режиме визуального геометрического программирования.
Последний способ избавляет пользователя от необходимости знать язык геометрического моделирования. Следует отметить, что языки геометрического моделирования, подобные приведенному в табл. 3, появились в 50-х годах одновременно с первыми алгоритмическими языками. За это время десятки тысяч технологов-программистов, не являющихся профессионалами в области информатики, успешно использовали их в своей деятельности для подготовки управляющих программ к станкам с ЧПУ.
Для представления экспертных инженерных знаний удобно использовать понятие "формальная продукционная система". Продукционная система представляет собой тройку
PS = <F, Р, I>,
где F — рабочая память системы, содержащая текущие данные; Р — база знаний, содержащая множество продукций; I — решатель, реализующий процедуры вывода.
В СПРУТ - технологии база знаний формируется из модулей инженерных знаний [3, 4]. Такой модуль представляет собой обобщенный функциональный блок, осуществляющий преобразование данных. Наиболее удачным и широко распространенным представлением функциональных блоков является стандарт IDEF0. В этом стандарте функциональный блок имеет конструкцию, приведенную на рис. 3.

Рис. 3. Функциональный блок IDEF0
В продукционных системах искусственного интеллекта элементом представления знаний является правило — продукция. Такие правила содержат предусловие, определяющее применимость его при определенном состоянии переменных базы данных (если (условие), то (действие»).
Приведенные выше теоретические схемы необходимо представить в форме, удобной для их определения человеком при вводе знаний в компьютер. Наиболее простой формой является таблица (рис. 4).
Модуль: <Имя>
Наименование: <Описание функции>
|
Наименование параметра |
Значение |
Имя |
|
1. 2. ВХОД (I) И УПРАВЛЕНИЕ (С) 3. |
УСЛОВИЕ (С) |
|
|
4. ВЫХОД (О) |
МЕХАНИЗМ (М) |
АДРЕС |
Рис. 4. Внешнее представление модуля инженерных знаний
Такая таблица содержит все элементы функционального блока, представленного на рис. 3. Наименования параметров должны выбираться из словаря системы, так же как и их имена — идентификаторы, необходимые для написания формул. Условие представляет собой ограничения, накладываемые на входные и управляющие параметры и задающие область определения функции, реализуемой модулем.
Модули инженерных знаний (МИЗ) должны реализовать следующие функции:
· присваивание значений выходным переменным;
· определение значений по таблицам (рис. 5);
· определение значений выбором из базы данных;
· вычисление значений по формулам;
· вычисление значений с помощью программных модулей;
· построение геометрических образов.
Модуль: block5
Разработчик: Г. Евгенев
Наименование: назначение стандартной длины
Источник информации: Анурьев В.И. Справочник конструктора, т. 2
|
Наименование параметра |
Значение |
Имя |
|
1. Наименование детали
2. Диаметр оси стандартный, мм 3. Длина оси исходная, мм |
Ось гладкая, ось с буртиком (0,50] (0,300] |
b1
a1 a12 |
|
4. Длина оси стандартная, мм |
TABL |
a2 |
TABL1
|
Длина оси исходная, мм |
Диаметр оси стандартный, мм |
|||||||
|
5 |
6 |
8 |
10 |
12 |
16,18 |
20 |
22 |
|
|
(25,28] (28,30] |
28 30 |
28 30 |
28 30 |
28 30 |
28 30 |
28 30 |
30 |
|
Рис. 5. Внешнее представление модуля — таблицы
Математические и геометрические модели подключаются в методы объектов с помощью соответствующих МИЗ.
Третий уровень знаний включает структурированные системы предыдущих уровней. Структурированная исходная система будет рассмотрена ниже. Носителем модели структурированной системы данных в соответствии со стандартом IDEF1 являются объекты и мощности отношений между ними: О — ноль, один или более; Р — один или более; Z — ноль или один; N — в точности N. Мощность показывает, какое число экземпляров объекта-потомка может существовать для каждого экземпляра объекта-родителя. Сигнатура модели определяет структуру базы данных, изображаемую в IDEF1 в виде графа специального вида.
Модель структурированной порождающей системы имеет в качестве носителей правила-продукции и их переменные, а сигнатура представляется семантической сетью, на которой решатель осуществляет процедуры логического вывода.
Агент — краеугольный камень новой парадигмы
Агент —- это развитие известного понятия объект, представляющего абстракцию множества экземпляров предметов реального мира, имеющих одни и те же свойства и правила поведения [3]. Свойства объекта описываются исходной системой, а правила поведения — порождающей системой, чаще всего структурированной (рис. 6). Состояние объекта определяется перечнем его свойств с текущими значениями. Объект со значениями всех его свойств определяет экземпляр, моделью которого является кортеж соответствующего реляционного отношения из системы данных. В число свойств объекта включаются его идентификатор, а также указывающие, описывающие и вспомогательные атрибуты. Последние два типа атрибутов делятся по отношению к методу объекта на входные и выходные (рис. 6). Описательные атрибуты определяют свойства, внутренне присущие объекту, а вспомогательные — его структурные связи с экземплярами других объектов.

Рис. 6. Модель интеллектуального агента
Интеллектуальным является объект, поведение которого определяет база знаний. Активный объект, или агент, — это объект, способный изменять свое состояние, используя информацию о состоянии смежных объектов. Для этого агенты объединяются в структурированную исходную систему, называемую мультиагентной. Носителем модели такой системы являются объекты и их свойства, а сигнатурой — семантическая сеть, используемая операционной средой для передачи информации, активизирующей поведение агентов. В результате этого формируется некоторое множество экземпляров агентов, являющееся целью всего процесса.
Мультиагентная метасистема распределенного интеллекта
Высшей ступенью организации знаний являются мультиагентные системы распределенного интеллекта [3]. Они образуются наложением структуры И/ИЛИ графа на мультиагентную систему. На рис. 7 приведена такая структура применительно к проблематике автоматизированного проектирования изделий (межагентные информационные связи на этом рисунке не показаны).
На рис. 7, например, агенты A, В и C связаны с подчиненными по иерархии "целое-часть" агентами связями типа И, а агенты Е, L и S — связями типа ИЛИ. С помощью последних осуществляется синтез вариантов структур изделий, управляемый вспомогательными атрибутами агента-родителя. Параметрический синтез выполняется мультиагентной системой посредством использования методов агентов и обмена информацией между ними.
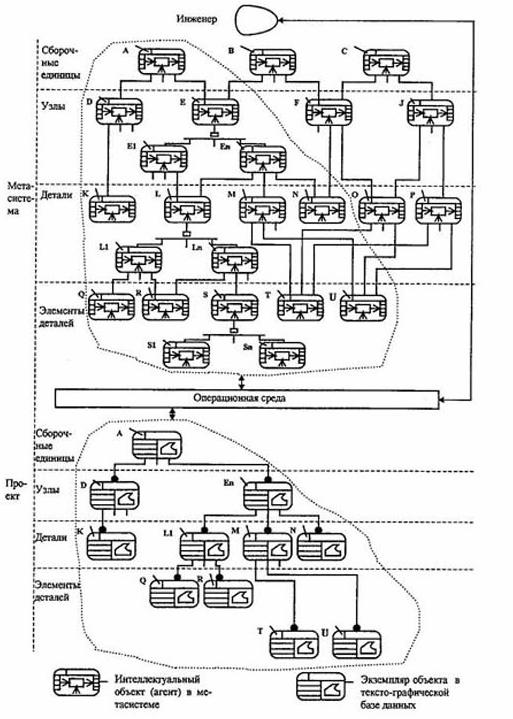
Рис. 7. Мультиагентная метасистема
Метасистема содержит знания обо всем множестве известных ее авторам вариантов решений. В результате проектирования, началом которого является ввод исходных данных в агент высшего уровня (например, A на рис. 7), получаются тексто-графические данные, содержащие проект одного экземпляра изделия, удовлетворяющего требованиям исходных данных.
* * *
Принципиальным отличием новой методологии от старой является то, что если при алгоритмическом подходе процессом управляют команды, использующие данные, то в новой технологии "бал правят" данные с помощью команд. Это происходит как на микроуровне внутри агентов, что дает основание говорить о распределенном интеллекте, так и на макроуровне — в мультиагентном пространстве.
Список литературы
1.Клир Дж. Системология. Автоматизация решения системных задач: Пер. с англ. М.: Радио и связь, 1989. 544 с.
2. Нариньяни А. С. Недоопределенность в системах представления и обработки знаний // Изв. АН СССР. Техническая кибернетика, 1986. № 5. С. 3—28.
3. Evgenev G. В. Multiagent methodology for computer aided design and integrated manufacturing // Globalization of Manufacturing in the Digital Communications of the 21-st Century: Innovation, Agility and the Virtual Enterprise. Proceedings of the Tenth International IFIP WG5.2/5.3Conference PROLAMAT-98, Trento, ITALY. Kluwer Academic Publishers, Boston/Dordrecht/ London, 1998. P. 591-602.
4. Evgenev G. B. Methodology of intelligent object-oriented design and process planning // Changing the Ways We Work. Shaping the ICT-solutions for the Next Century. Proceedings of the Conference on Integration in Manufacturing Goteborg, Sweden, 1998. P. 154-160.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 3, 1999
СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПОРЕКТИРОВАНИЯ
Ключевые слова: Моделирование, уровни знания, модели знания, иерархия моделей, искусственный интеллект, агенты.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



