научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#11 ноябрь 2005
Г. Н. Зверев, д-р техн. наук, Уфимский государственный технический университет
Логические аппроксимации, лапласовы оценки и корреляционная логика
Точные решения дискретно-логических задач с полной априорикой формализма частотной логики заменяются в реальных информационных ситуациях логическими приближениями, основанными на лапласовых оценках высших моментов по известным низшим, снижении размерности и экспоненциальной сложности логических задач.
Современные информационные технологии и их программно-аппаратные средства основаны на формализме классической логики с двоичной шкалой различимости {да, нет} и истинности {истина, ложь} → {1, 0}. Однако реальные информационные процессы оперируют искаженными, неполными, противоречивыми фактическими и априорными данными, которым вряд ли возможно приписать однозначную оценку 0 или 1 двоичной шкалы. В таких ситуациях более адекватным описанием является формализм частотной логики [1—3], в котором двоичная истинность заменяется частотной истинностью, а логические связи двоичных признаков, свойств и предикатов представлены различными частотными связями. Последние в пределе могут сколь угодно приближаться к строгим логическим оценкам и зависимостям.
Переход от предельных, недостижимых оценок истинности в двоичной шкале {1, 0} к числовым оценкам истинности в открытом интервале (0, 1) позволяет построить логические аппроксимации, которые учитывают искажения и неопределенности фактов и априорики. Целью данной статьи является построение оценок истинности логических методов и погрешностей истинности в корреляционном приближении.
Частотная истинность произвольного высказывания а (аргумента, предиката,
логической функции) определяется как частость (доля, шанс, вероятность)
значения а = 1 в конечном множестве информационных ситуаций: ![]() (где Na — численность единичных значений, N
— численность универсума ситуаций), а редкость значения a
= 1 определяет частотную меру ложности
(где Na — численность единичных значений, N
— численность универсума ситуаций), а редкость значения a
= 1 определяет частотную меру ложности
![]() или частость
значения a = 0.
или частость
значения a = 0.
Чтобы воспользоваться формулами и алгоритмами частотной логики, необходимо знать не только истинности исходных данных, но и все частотные связи между ними, которые определяются расстоянием, метрикой, ковариацией, корреляцией, гиперкорреляциями и понимаются в информационной семантике как меры информативности, возможности предсказания неизвестных или близости к логической связи между признаками.
В частотной логике основной характеристикой связи качественных двоичных
признаков служит смешанный момент ![]() — объем пересечения признаков,
по которому вычисляются другие характеристики явлений. Численные значения
моментов определяются по экспериментальным данным, теоретическим моделям либо
совместно обрабатывается фактическая и априорная информация. Получаемые
результаты наблюдения, моделирования и обработки обычно подвержены разного рода
искажениям, поэтому точные решения частотной логики можно упрощать, заменяя их
приближенными и субоптимальными логическими аппроксимациями. Идея логических
приближений в частотной шкале истинности основана на частотной упорядоченности
признаков и связей между ними, а также на сильной зависимости моментов, которая
используется при построении корреляционной логики. Эта идея способствует
решению основной проблемы дедукции — NP-сложности
логических задач.
— объем пересечения признаков,
по которому вычисляются другие характеристики явлений. Численные значения
моментов определяются по экспериментальным данным, теоретическим моделям либо
совместно обрабатывается фактическая и априорная информация. Получаемые
результаты наблюдения, моделирования и обработки обычно подвержены разного рода
искажениям, поэтому точные решения частотной логики можно упрощать, заменяя их
приближенными и субоптимальными логическими аппроксимациями. Идея логических
приближений в частотной шкале истинности основана на частотной упорядоченности
признаков и связей между ними, а также на сильной зависимости моментов, которая
используется при построении корреляционной логики. Эта идея способствует
решению основной проблемы дедукции — NP-сложности
логических задач.
Корреляционные методы, широко распространенные при решении задач с
непрерывными количественными переменными, предполагают знание первых двух
моментов распределения векторных величин. Для дискретно-логических задач также
полагаем известными только первый  либо второй
либо второй  моменты распределения
вектора двоичных признаков z = (z1, z2,…,
zn)T,
где N — число ситуаций
(или объектов) предметной области; n — число
двоичных признаков объектов, известных, искомых, вычисляемых; Т — знак
транспонирования.
моменты распределения
вектора двоичных признаков z = (z1, z2,…,
zn)T,
где N — число ситуаций
(или объектов) предметной области; n — число
двоичных признаков объектов, известных, искомых, вычисляемых; Т — знак
транспонирования.
Первый момент M(z)
есть вектор размерности n, компоненты которого
определяют "объемы" qj
признаков zi = 1 переменных zi, принимающих в одной из N ситуаций
значение 0 или 1: 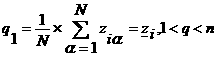 . Величина qi - есть частость единичного значения zi,
мера истинности высказывания "объект предметики обладает свойством
. Величина qi - есть частость единичного значения zi,
мера истинности высказывания "объект предметики обладает свойством ![]() .
.
Второй момент M(zzT)
есть симметричная квадратная матрица порядка n,
в диагонали которой стоит первый момент, так как ![]() 02 = 0, 12
= 1, а недиагональные элементы выражают объемы парных пересечений
02 = 0, 12
= 1, а недиагональные элементы выражают объемы парных пересечений ![]() мера
истинности высказывания “объект обладает свойствами zi и zj”, qij = qji.
мера
истинности высказывания “объект обладает свойствами zi и zj”, qij = qji.
Этой информации достаточно для точного вычисления объемов составных признаков, которые получаются унарными и бинарными логическими операциями из заданных входных признаков, но недостаточно для выражения частотных связей нового признака с признаками, отличными от входных.
Обозначим входные признаки двоичной логической операции f через zi
и zj объемами qi,
qj и пересечением qij, а новый составной признак z = f(zi,
zj) будет иметь объем qz и пересечения qiz,
qij. Здесь f — одна из шестнадцати возможных бинарных логических
операций, из них девять функций выражают особенности остальных: ![]() , — отрицание;
zi + zj
— сложение (дизъюнкция); zi,zj — умножение (конъюнкция); zi → zj — импликация; zi - zj— вычитание;
zi
, — отрицание;
zi + zj
— сложение (дизъюнкция); zi,zj — умножение (конъюнкция); zi → zj — импликация; zi - zj— вычитание;
zi ![]() zj
— эквиваленция; zi
zj
— эквиваленция; zi
![]() zj — сложение по модулю 2 (антиэквиваленция);
zi |zj
— И-НЕ (штрих Шеффера); zi ↓ zj -
ИЛИ-НЕ (стрелка Пирса). Признак, отличный от zi,zj обозначим zk,
его объем qk и парные пересечения qik, qjk,
qkz тройное пересечение — третий
момент qijk. Выражения частотной
истинности составных признаков представлены в таблице.
zj — сложение по модулю 2 (антиэквиваленция);
zi |zj
— И-НЕ (штрих Шеффера); zi ↓ zj -
ИЛИ-НЕ (стрелка Пирса). Признак, отличный от zi,zj обозначим zk,
его объем qk и парные пересечения qik, qjk,
qkz тройное пересечение — третий
момент qijk. Выражения частотной
истинности составных признаков представлены в таблице.
В первой колонке добавлены полиномиальные (дизъюнктивные) формы логических операций. Используя эти формулы, можно последовательно наращивать логические структуры и получать моменты все более сложных составных признаков. Однако в последнем столбце присутствует неизвестный объем тройного пересечения qijk признаков zi, zj, zk, который выводит оценки истинности из корреляционной теории. Чтобы остаться в рамках корреляционного приближения и избежать вычисления многомерных матриц и интегралов, необходимо найти оценки третьего момента по первым двум и выразить достигаемую точность приближения. В этом и заключается суть корреляционной логики при построении оценок истинности в частотной шкале, их погрешностей и последующем применении их в дискретно-логических задачах принятия оптимальных решений.
|
z = f(zi, zj) |
qz |
qik |
qjz |
qijz |
qkz |
|
|
1 - qi |
0 |
qj - qij |
0 |
qk - qik |
|
zizj |
qij |
qij |
qij |
qij |
qijk |
|
zi + zj |
qi + qj - qij |
qi |
qj |
qij |
qik + qjk - qijk |
|
|
1 - qi + qij |
qij |
qj |
qij |
qk - qjk + qijk |
|
|
qi - qij |
qi - qij |
0 |
0 |
qik - qijk |
|
|
1 - qi - qj +2qij |
qij |
qij |
qij |
qk - qik - qjk + 2qijk |
|
|
qi + qj – 2qij |
qi - qij |
qj - qij |
0 |
qik + qjk – 2qijk |
|
|
1 - qij |
qi - qij |
qj - qij |
0 |
qk - qijk |
|
|
1 – qi – qj +qij |
0 |
0 |
0 |
qk – qik – qjk + qijk |
Если удастся достаточно точно оценить третий момент по двум первым, то алгоритмы поиска оптимальной или субоптимальной аппроксимации существенно упрощаются, так как не требуется вычислять многомерные интегралы и матрицы моментов, перемножать логические полиномы и их отрицания, а достаточно последовательно наращивать матрицу вторых моментов M(zzT) составными аппроксимирующими признаками и информативными импликатами и коррелятами.
Найдем граничные значения неизвестного тройного пересечения — момента третьего порядка q = qijk = M(zi • zj • zk) исходя из априорного значения моментов первого и второго порядка: qi, qj, qk, qij, qik, qjk и пусть для определенности qi, ≤ qj, ≤ qk. Параметры априорики должны быть согласованы между собой и удовлетворять естественным ограничениям:
0 ≤ qi,…,qk ≤ 1, bij ≤ qij ≤ qi, bik ≤ qik ≤ qi, bjk ≤ qjk ≤ qj.
где bij = max(0, qi + qj - 1), bik = max(0, qi + qk - 1), bjk = max(0, qj + qk — 1) — параметры зазоров между универсумом ситуаций и суммой объемов двух признаков.
Для вывода этих выражений воспользуемся одномерной диаграммой Эйлера с интервалами — признаками в единичном универсуме и разместим объекты универсума, обладающие признаком zk = 1, в начале универсума [0, 1], а затем объекты со свойством zj = 1, тогда минимально возможное значение второго момента qjk при известных qj и qk определяется предельным правым положением интервала Эйлера признака zj (рис. 1, показано штрихом) и равно либо 0 для малых признаков при qk ≤ 1 - qj, либо qj + qk - 1 для больших признаков при qk > 1 - qj.
Отсюда следует ограничение значений второго момента по известным первым
моментам: qjk, ≤ qjk ≤ qj и в качестве оценки qjk
берется середина интервала неопределенности  с предельной ошибкой этой оценки
с предельной ошибкой этой оценки
 .
.
Такого типа оценки частостей являются наилучшими по точности, если
вариации неизвестных априорных данных симметричны в допустимом интервале, и
называются лапласовыми оценками при равномерном распределении частостей qjk, .... Если ошибка ![]() меньше допустимой, то
более точный расчет второго момента qjk
становится излишним.
меньше допустимой, то
более точный расчет второго момента qjk
становится излишним.
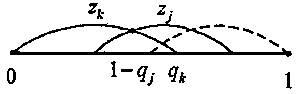
Рис. 1
Граничные значения неизвестного третьего момента q
= qijk в одномоментном приближении
отыскиваются по той же схеме. Прежде найдем оценки верхнего и нижнего пределов
объема тройного пересечения qmin, ≤ q ≤ qmax из априорного знания только первых моментов.
Добавим в одномерной диаграмме Эйлера наименьший признак zi,
его необходимо представить в общем случае двумя несвязными интервалами
суммарной длиной qi. Верхняя граница qmax определяется
объемом минимального признака при вложенности трех признаков, а нижняя граница
— таким размещением в универсуме объектов со свойством zi
= 1, которое по возможности не образует тройного пересечения в интервалах [0,1 -
qj] и [qk,
1]. Отсюда при qi > 1 - qj + 1 - qk
обязательно возникнет тройное пересечение q >
0, следовательно, первые моменты ограничивают искомую величину q снизу, если признаки большие, при S1
= qi + qj
+ qk > 2, значит, qmin = max(0, S1 - 2), qmax = qi лапласова оценка
третьего момента ![]() с ошибкой
с ошибкой ![]() .
.
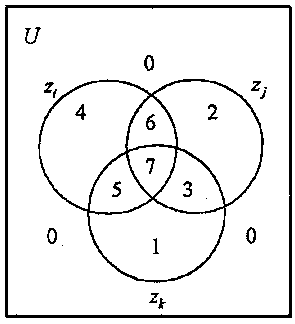
Рис. 2
Для определения границ q в корреляционном, двухмоментном приближении по известным первым и вторым моментам трех признаков представим на двумерной диаграмме Эйлера (рис. 2) случай общего положения, при котором признаки разбивают универсум на максимальное число 23 = 8 классов объектов, различимых по этим свойствам и занумеруем эти классы в соответствии с двоичным представлением числа zj zj zk от 0 = 000 до 7 = 111. Объемы элементарных классов выражаются через трехмоментную априори ку так:
q0 = 1 – S1 + S2 – q; q1 = qk – qik – qjk + q;
q3 = qjk – q; q2 = qj – qij – qjk + q;
q5 = qik – q; q4 = qi – qij – qik + q;
q6 = qij – q; q7 = q,
где суммы первых и вторых моментов есть S1 = qi + qj + qk, S2 = qij + qik + qjk. В эти формулы входит неизвестная величина q слева со знаком минус, справа — со знаком плюс. Объемы классов q0, q1,..., q7 не могут быть отрицательными, поэтому из левой группы получаем четыре ограничения величины тройного пересечения снизу, а из правой группы — ограничения сверху, и из них выбираем наиболее сильные ограничения: qmin = max(0, bi, bj, bk), где зазоры qmax = min(qij, qik, qjk, S0), сумма . В этих формулах не предполагается упорядоченность признаков zi, zj, zk по их объемам.
Легко проверить, что одномоментные ограничения q снизу и сверху в двухмоментном приближении становятся излишними, но все величины, входящие в qmin и qmax, являются значимыми и определяют лапласову оценку третьего момента и его максимальной ошибки
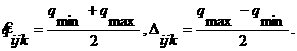
Найдем условия, при которых интервал [qmin, qmax] неопределенности qijk стягивается в точку. Во-первых, это случай отрицательной логической связи хотя бы одной пары признаков, например rij=-1, тогда qij = 0, bi ≤ 0, qmin = qmax = qijk = 0. Во-вторых, при сильной положительной связи любой пары признаков, скажем, rij → 1, интервал неопределенности также стягивается в точку. В самом деле, при вложении меньшего признака в больший два элементарных класса из восьми исчезают, например, при вложении zi → zj сразу следует q4 = q5 = 0, отсюда qjk = qik. Следовательно, сильные положительные и отрицательные корреляционные связи могут, не уменьшая третьи моменты, резко повышать точность логических аппроксимаций в корреляционном приближении.
Итак, если хотя бы один из коэффициентов корреляции rij,
rik, rjk по модулю равен единице, то третий момент вычисляется точно:
qijk = qmin = qmax. Максимальная погрешность корреляционной логики
проявляется в ситуациях с попарной независимостью признаков rij = rik
= rjk = 0. При полной независимости
признаков справедлива точная оценка ![]() которая служит простейшей
аппроксимацией третьего момента. Были предложены и другие аппроксимации,
например, в [1]. В двухмоментном приближении простой вид имеет формула
которая служит простейшей
аппроксимацией третьего момента. Были предложены и другие аппроксимации,
например, в [1]. В двухмоментном приближении простой вид имеет формула  , которая в
случае попарной независимости совпадает с предыдущим выражением, основанным на
гипотезе полной независимости признаков. Точность этих приближений зависит от
размеров признаков и уровня тернарной и парных связей между ними.
, которая в
случае попарной независимости совпадает с предыдущим выражением, основанным на
гипотезе полной независимости признаков. Точность этих приближений зависит от
размеров признаков и уровня тернарной и парных связей между ними.
Найдем предельные ошибки оценок тройного пересечения признаков в наиболее неблагоприятном случае попарной независимости признаков: rij = rik = rjk = 0; полагая упорядоченность их объемов qi ≤ qj ≤ qk. Учитывая соотношения некоррелированности qij = qiqj, qik =qiqk, qik = qjqk легко найти минимальное значение третьего момента qmin = max(0, bj); максимальное значение qijk находится по минимуму qij и S0. Найдем разность этих величин:
qij – S0 = qij – 1 + qi +qj + qk – qij – qik – qjk = (1 - qk) (qi = qj - 1),
значит, qmin = qiqj для малых признаков (qi + qj < 1) и qmin = S0 для больших признаков. В результате получаем три интервала неопределенности тройного пересечения попарно независимых признаков, определяемые по точно заданным моментам первого и второго порядка:
0 ≤ qijk ≤qij при qj + qk ≤ 1;
bi ≤ qijk ≤ qij при qi + qj ≤ 1≤ qj +qk;
qi ≤ qijk ≤S0 при qi + qj >1.
В итоге получаем оценки сверху точности двухмоментного приближения, qi ≤ qj ≤ qk.

которые
определяют границы применимости чистой корреляционной логики без привлечения
иных оценок высших моментов. В ситуациях с недопустимо высоким уровнем
погрешности ![]() момент
qijk должен оцениваться
внелогическими методами. Следует заметить, что погрешность приближения не
зависит от способа кодировки номинативных признаков, и переход от признаков к
их отрицаниям, скажем, от больших позитивных к малым негативным, не изменяет точность
аппроксимации, в то время как коэффициент корреляции признаков может сильно
измениться при переходе к другой арифметизации номинативных признаков. Это
обусловлено характером зависимости qijk
от априорики J, определяющей фактически семь
независимых уравнений от восьми неизвестных объемов элементарных классов.
момент
qijk должен оцениваться
внелогическими методами. Следует заметить, что погрешность приближения не
зависит от способа кодировки номинативных признаков, и переход от признаков к
их отрицаниям, скажем, от больших позитивных к малым негативным, не изменяет точность
аппроксимации, в то время как коэффициент корреляции признаков может сильно
измениться при переходе к другой арифметизации номинативных признаков. Это
обусловлено характером зависимости qijk
от априорики J, определяющей фактически семь
независимых уравнений от восьми неизвестных объемов элементарных классов.
С ростом числа признаков экспоненциально увеличивается сложность дискретно-логических задач, но одновременно экспоненциально возрастает и частотная зависимость между признаками и уменьшение их совокупной информативности, что увеличивает возможности логических аппроксимаций. Мера зависимости определяется гиперкорреляцией и частотной связностью.
Гиперковариацию трех признаков определим так же, как парную ковариацию: если признаки независимы, то qijk = qiqjqk, поэтому тернарная ковариация Kijk = qijk - qiqjqk. Минимальное значение она приобретает при нулевом третьем моменте (qijk = 0), тогда Kijk = - qiqjqk, для этого достаточно (но не необходимо), чтобы одна из трех парных связей стала предельной отрицательной, скажем, rij = -1. Максимального значения тройная ковариация достигает при вложении меньшего признака zi в пересечение zjzk оставшихся больших zi ≤ zjzk, тогда qijk = qi = qij = qik ≤ qjk, и наибольшая гиперковариация есть maxKijk = qijk – qiqjqk = qi(1 - qjqk). Следовательно, множественный коэффициент корреляции трех битовых признаков — гиперкорреляция, удовлетворяющая условию нормировки -1 ≤ rijk ≤1, определяется формулой
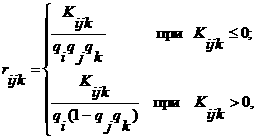
где qi ≤ qj ≤ qk. Эта формула легко переносится на произвольное число признаков и моменты высших порядков; в частности, при qk = 1 она воспроизводит парную корреляцию rij.
Введенная гиперкорреляция, как и в случае парных связей, обладает тем
недостатком, что не всегда отражает близость к предельной логической
зависимости признаков, например, мера rijk
= 0 — признаки некоррелированы, но существует логическая связь — импликация
zizj →
zk, когда пересечение двух признаков
целиком лежит в третьем признаке. Логическая связь между двоичными признаками
или их отрицаниями возникает в случае, если хотя бы один из моментов ![]() произведения
признаков равен нулю, т. е. признаки не пересекаются и удовлетворяют уравнению
произведения
признаков равен нулю, т. е. признаки не пересекаются и удовлетворяют уравнению ![]() , здесь
, здесь ![]() . Аналогом
корреляционного отношения для качественных признаков является их максимальная
частотная связность
. Аналогом
корреляционного отношения для качественных признаков является их максимальная
частотная связность ![]() , которая при
, которая при ![]() принимает значения
предельной (логической) связности sm = 1. Максимальная связность трех признаков лежит в интервале
принимает значения
предельной (логической) связности sm = 1. Максимальная связность трех признаков лежит в интервале
![]() , а
в общем случае k признаков предельный уровень
момента
, а
в общем случае k признаков предельный уровень
момента ![]() ,
отсюда 1 – 2-k ≤ sm ≤ 1, т. е. с ростом числа признаков экспоненциально
уменьшается добавочная полезная информация.
,
отсюда 1 – 2-k ≤ sm ≤ 1, т. е. с ростом числа признаков экспоненциально
уменьшается добавочная полезная информация.
Рассмотрим пример использования аппарата корреляционной логики для оценки
достоверности логического вывода по схеме отделения модус поненс: a, a →
b|- b — "если истинны высказывания "а" и
"из а следует b", то высказывание
"b" также истинно". В реальности
факт а и правило a →
b не бывают абсолютно истинными, поэтому интересно
оценить ошибки ![]() заключения b
по известным ожидаемым искажениям факта и правила. Пусть задан информационный
процесс выявления ВИЧ инфицированных b = 1
пациентов по результатам анализа крови a — по
наличию антител в крови пациента a = 1. Ошибки посылки a связаны
с лабораторными погрешностями v, влияющими на
результат анализа:
заключения b
по известным ожидаемым искажениям факта и правила. Пусть задан информационный
процесс выявления ВИЧ инфицированных b = 1
пациентов по результатам анализа крови a — по
наличию антител в крови пациента a = 1. Ошибки посылки a связаны
с лабораторными погрешностями v, влияющими на
результат анализа: ![]() — при отсутствии ошибки
лабораторного анализа (v = 0) оценка
— при отсутствии ошибки
лабораторного анализа (v = 0) оценка ![]() , а при ее
наличии (v = 1) оценка
, а при ее
наличии (v = 1) оценка ![]() . Ошибки идеального
логического правила a →
b по формулам частотной логики (см. таблицу)
равны ошибке импликации
. Ошибки идеального
логического правила a →
b по формулам частотной логики (см. таблицу)
равны ошибке импликации ![]() в ситуациях a
= 1, b = 1. В реальной импликации а заменяется
на оценку:
в ситуациях a
= 1, b = 1. В реальной импликации а заменяется
на оценку: ![]() .
Истинность этого логического полинома по формулам частотной логики равна
.
Истинность этого логического полинома по формулам частотной логики равна ![]() , остальные
произведения признаков равны нулю.
, остальные
произведения признаков равны нулю.
Ошибка логического вывода ![]() .
.
В корреляционном приближении последнее слагаемое неизвестно и оценивается
по объемам признаков и их парных пересечений. Например, a
= 0,55, b = 0,5, ab
= 0,45, v = 0,06, av
= 0,04, bv = 0,03, тогда оценка тройного
пересечения по формулам корреляционной логики лежит в интервале 0,01 ≤ abv ≤ 0,03, т. е. qijk = 0,02 + 0,01. Ошибка чистой
позитивной импликации a → b — "если в крови есть антитела, то пациент
поражен СПИДом" равна ![]() = a - ab= 10%, оценка
ошибки реальной импликации в корреляционном приближении
= a - ab= 10%, оценка
ошибки реальной импликации в корреляционном приближении ![]() , т. е. ошибки
наблюдений v частично скомпенсируют ошибку чистой
импликации, а ошибка обратной импликации b → a, равной
чистой негативной импликации
, т. е. ошибки
наблюдений v частично скомпенсируют ошибку чистой
импликации, а ошибка обратной импликации b → a, равной
чистой негативной импликации ![]() — "если в крови нет
антител, то пациент не поражен СПИДом", равна b
— ab = 5%.
— "если в крови нет
антител, то пациент не поражен СПИДом", равна b
— ab = 5%.
Список литературы
1. Зверев Г. Н. Оценка надежности и оптимизация качественной интерпретации // Техника и технология геофизических исследований скважин. Уфа: Изд. БашНИПИнефть, 1979. С. 145-155.
2. Зверев Г. Н. Основания теоретической информатики. Разд. 1—7 Уфа: УГАТУ, 1997. 97 с.
3. Зверев Г. Н. Точные и аппроксимационные логики в машинных рассуждениях // Тр. V нац. конференции по искусственному интеллекту. Т. 1. Казань. 1996. С. 62—66.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 2, 1999
ИНТЕЛЛЕКТУАЛЬНЫЕ СИСТЕМЫ
Ключевые слова: Дискретная логика, частотная логика, методы корреляции, частотная связность признаков, корреляция моментов высших порядков.
Публикации с ключевыми словами: Дискретная логика, частотная логика, методы корреляции, частотная связность признаков, корреляция моментов высших порядков
Публикации со словами: Дискретная логика, частотная логика, методы корреляции, частотная связность признаков, корреляция моментов высших порядков
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



