научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#11 ноябрь 2005
В. И. Левин, д-р техн. наук, проф., Пензенский технологический институт
Интервальный подход к оптимизации в условиях неопределенности
Дана постановка и обоснование задачи оптимизации в условиях интервальной неопределенности. Представлены основные сведения о сравнении интервалов и выборе большего и меньшего интервалов. Приведено полное решение трех задач дискретной интервальной оптимизации.
Постановка задачи
Большинство современных задач оптимизации решается в предположении детерминированных параметров оптимизируемой системы. Однако на практике системы в технике, экономике, социологии и т. д. имеют, как правило, недетерминированные параметры. Оптимизация таких систем выдвигает ряд новых трудных проблем: сравнение недетерминированных величин, обобщение понятия оптимума на недетерминированный случай, выяснение условий его существования, конструирование алгоритмов его отыскания. В статье дан обзор некоторых работ в этой области. При этом изучается наиболее простой и естественный случай, когда недетерминированность оптимизируемой системы выражается в том, что ее параметры заданы лишь с точностью до интервалов возможных значений. Интервальные оценки параметров систем обычно находятся экспертным путем либо с помощью приближенных вычислений или измерений.
Общая задача оптимизации в интервальной постановке такова. Задана функция
![]() (1)
(1)
где x = (х1,..., хn) — вектор аргументов, причем ![]() и X
— числовое множество;
и X
— числовое множество; ![]() — вектор интервальных параметров,
т. е. параметры
— вектор интервальных параметров,
т. е. параметры ![]() — замкнутые интервалы
— замкнутые интервалы ![]() , в которых
находятся возможные значения этих параметров. Каждому значению аргумента
, в которых
находятся возможные значения этих параметров. Каждому значению аргумента ![]() , согласно (1)
соответствует одно значение функции в виде некоторого интервала
, согласно (1)
соответствует одно значение функции в виде некоторого интервала ![]() . Необходимо
найти значение аргумента
. Необходимо
найти значение аргумента ![]() , для которого соответствующее значение
функции
, для которого соответствующее значение
функции ![]() экстремально
(максимально или минимально). В данной статье мы ограничимся задачами дискретной
оптимизации, в которых множество X возможных
значений переменных дискретно.
экстремально
(максимально или минимально). В данной статье мы ограничимся задачами дискретной
оптимизации, в которых множество X возможных
значений переменных дискретно.
Сравнение интервалов
Для решения сформулированной задачи необходимо уметь сравнивать интервалы
и выделять из них экстремальные. Введем детерминированные операции непрерывной
логики: ![]() (дизъюнкция),
(дизъюнкция),
![]() (конъюнкция)
и далее — соответствующие недетерминированные (в частности, интервальные)
операции этой логики:
(конъюнкция)
и далее — соответствующие недетерминированные (в частности, интервальные)
операции этой логики:
 (2)
(2)
где ![]() и
и ![]() — любые
числовые множества (в частности, интервалы). Как видно из (2), дизъюнкция
(конъюнкция) двух числовых множеств определяется как множество возможных
значений дизъюнкции (конъюнкции) двух чисел в условиях, когда эти числа
пробегают независимо друг от друга все возможные значения внутри
соответствующих числовых множеств.
— любые
числовые множества (в частности, интервалы). Как видно из (2), дизъюнкция
(конъюнкция) двух числовых множеств определяется как множество возможных
значений дизъюнкции (конъюнкции) двух чисел в условиях, когда эти числа
пробегают независимо друг от друга все возможные значения внутри
соответствующих числовых множеств.
Следуя [1], введем отношение неравенства интервалов в виде эквивалентности
![]() (3)
(3)
Как известно [1], два интервала ![]() и
и ![]() , такие, что
, такие, что ![]() ≥
≥ ![]() или
или ![]() ≥
≥ ![]() , называются
сравнимыми по отношению ≥, другие
, называются
сравнимыми по отношению ≥, другие ![]() и
и ![]() называются несравнимыми по этому
отношению. В системе интервалов
называются несравнимыми по этому
отношению. В системе интервалов ![]() , интервал a
, интервал a ![]() называется максимальным
(минимальным), если он сравним с интервалами
называется максимальным
(минимальным), если он сравним с интервалами ![]() , по отношению ≥ и
, по отношению ≥ и ![]() .
.
В работе [1] были получены следующие важные результаты.
Теорема 1. Для того чтобы интервалы ![]() и
и ![]() были сравнимы и в отношении
были сравнимы и в отношении ![]() ≥
≥ ![]() (несравнимы),
необходимо и достаточно, выполнения условия a1
≥ b1, a2
≥ b2 (выполнения условий a1 < b1,
a2 > b2
или a1, b2,
> a2).
(несравнимы),
необходимо и достаточно, выполнения условия a1
≥ b1, a2
≥ b2 (выполнения условий a1 < b1,
a2 > b2
или a1, b2,
> a2).
Теорема 2. Для того чтобы в системе интервалов, интервал 3\ был максимальным, необходимо и достаточно, чтобы выполнялись условия
![]() (4)
(4)
а для того,
чтобы ![]() был
минимальным, необходимо и достаточно выполнения условий
был
минимальным, необходимо и достаточно выполнения условий
![]() (5)
(5)
Результаты теоремы 1 позволяют сравнивать интервалы, распространять на них понятие оптимума и выяснять условие существования такого оптимума. Результаты теоремы 2 позволяют строить алгоритмы выделения экстремальных интервалов, сводя их к алгоритмам выделения экстремальных точечных величин. Это дает возможность сводить интервальные оптимизационные задачи к детерминированным, что и составляет основу для решения интервальных задач.
Задача о назначениях
В качестве первого примера применения изложенного подхода рассмотрим
задачу о назначениях. Интервальная задача о назначениях на должности состоит в
распределении n должностей между n претендентами так, чтобы минимизировать суммарные
издержки по работе. При этом издержки от работы каждого претендента на каждой
должности задаются с точностью до интервала. Математически эта задача состоит в
отыскании булевой матрицы назначений Х= ||xij||,
обращающей в минимум сумму издержек ![]() где
где ![]() — заданная матрица издержек;
— заданная матрица издержек; ![]() — издержки от
работы в j-й должности i-го
претендента. При этом элементы
— издержки от
работы в j-й должности i-го
претендента. При этом элементы ![]() — интервальные величины вида
отрезков
— интервальные величины вида
отрезков ![]() =[aij1, aij2],
в которых рассеяны значения
=[aij1, aij2],
в которых рассеяны значения ![]() . Соответственно
. Соответственно ![]() оказывается
интервальной матрицей вида
оказывается
интервальной матрицей вида ![]() =[A1,A2], где A1
= ||aij1||, А2
= ||aij2|| Искомая матрица
X должна удовлетворять обычным условиям
нормировки
=[A1,A2], где A1
= ||aij1||, А2
= ||aij2|| Искомая матрица
X должна удовлетворять обычным условиям
нормировки ![]()
Задача о назначениях является простейшей моделью оптимального выбора
назначений на должность. При этом xjj
= 1 означает выбор для j-й должности i-го претендента (чему соответствуют издержки ![]() ). Для решения
задачи необходимо сравнение интервальных величин. Последнее выполняется
согласно изложенному выше. При этом получаем следующие результаты [2].
). Для решения
задачи необходимо сравнение интервальных величин. Последнее выполняется
согласно изложенному выше. При этом получаем следующие результаты [2].
Теорема 3. Для того чтобы интервальная задача о назначениях на
должности с матрицей издержек ![]() имела
решение X = ||хij||,
необходимо и достаточно, чтобы это же решение имели две детерминированные
задачи о назначениях с матрицами издержек А1 и А2.
имела
решение X = ||хij||,
необходимо и достаточно, чтобы это же решение имели две детерминированные
задачи о назначениях с матрицами издержек А1 и А2.
Теорема 4. Множество всех решений интервальной задачи о назначениях
на должности с матрицей издержек ![]() равно пересечению множеств
решений двух детерминированных задач о назначениях с матрицами издержек А1
и А2.
равно пересечению множеств
решений двух детерминированных задач о назначениях с матрицами издержек А1
и А2.
Теоремы 3, 4 сводят решение интервальной задачи о назначениях на должности к решению двух детерминированных задач о назначениях, которые естественно назвать нижней и верхней граничными задачами; их матрицы издержек равны соответственно А1 и А2.
Из изложенного следует алгоритм решения интервальной задачи назначения
на должности с интервальной матрицей издержек ![]() .
.
Шаг 1. Отыскание множества решений Мн нижней граничной задачи, т, е. детерминированной задачи о назначениях с матрицей издержек А1. Для этого можно использовать: метод ветвей и границ (он позволяет при небольшом числе должностей n быстро и просто получить решение); метод, основанный на вычислении логических определителей [2] (позволяет при небольших n получать решение и анализировать его при варьировании элементов матрицы А1); венгерский метод [3] (дает возможность находить решение при больших n); метод случайного поиска (позволяет быстро найти приближенное решение) [4].
Шаг 2. Отыскание множества решений Мв верхней граничной задачи, т. е. детерминированной задачи о назначениях с матрицей издержек А2, с использованием тех же методов, что и на шаге 1.
Шаг 3. Нахождение пересечения М множеств Мн и Мв. Для этого перебираются элементы одного множества и помечаются те из них, которые входят во второе множество. Если М ≠ Ø (непустое множество), то любая булева матрица назначений Хk из Месть решение данной интервальной задачи о назначениях на должности. Если же М ≠ Ø (пустое множество), то данная задача не имеет решения.
Задача булева линейного программирования
В качестве второго примера рассмотрим задачу булева линейного программирования. Задача булева линейного программирования с интервальными коэффициентами формулируется так:
![]() (6)
(6)
![]() (7)
(7)
Х1, ..., Хn = 0 или 1 (булевость переменных). (8)
Здесь ![]() —
замкнутые интервалы возможных значений коэффициентов. Введем в задаче (6)—(8)
интервальную матрицу коэффициентов
—
замкнутые интервалы возможных значений коэффициентов. Введем в задаче (6)—(8)
интервальную матрицу коэффициентов ![]() где
где ![]() матрица минимальных,
матрица минимальных, ![]() — матрица максимальных
коэффициентов; интервальный вектор коэффициентов целевой функции
— матрица максимальных
коэффициентов; интервальный вектор коэффициентов целевой функции ![]() где
где ![]() -
вектор минимальных, а с2 = \\ci2\\ — вектор
максимальных коэффициентов; интервальный вектор свободных членов
-
вектор минимальных, а с2 = \\ci2\\ — вектор
максимальных коэффициентов; интервальный вектор свободных членов ![]() , где b1 — вектор минимальных, а b2 — вектор максимальных свободных членов.
, где b1 — вектор минимальных, а b2 — вектор максимальных свободных членов.
Назовем нижней (верхней) граничной задачей для задачи (6)—(8) задачу булева линейного программирования с детерминированными коэффициентами, в которой:
· вектор коэффициентов целевой функции (6) равен c1, а целевая функция соответственно этому есть Q1(X) (вектор равен c2, а функция есть Q2(X);
· система ограничений (7) есть совокупность двух систем этого типа: с матрицей коэффициентов А1 и вектором свободных членов b1 и с матрицей коэффициентов А2 и вектором свободных членов b2;
· верны ограничения (8).
Будем сравнивать интервальные величины в соответствии с вышеизложенным. Тогда получим следующий основной результат [5].
Теорема 5. Для того чтобы задача булева линейного программирования с интервальными коэффициентами (6)—(8) имела решение х* = (х*,..., х*), необходимо и достаточно, чтобы это же решение имели две задачи булева линейного программирования с детерминированными коэффициентами: нижняя граничная задача задачи (6)—(8) и ее верхняя граничная задача.
По теореме 5 множество всех решений задачи (6)—(8) есть пересечение множеств решений ее нижней и верхней граничных задач, т. е. решение интервальной задачи булева линейного программирования также сводится к решению двух детерминированных задач булевого линейного программирования. Отсюда следует очевидный алгоритм нахождения множества всех решений задачи, пригодный при небольших размерностях задачи n.
Шаг 1. Формирование нижней и верхней граничных задач имеющейся
интервальной задачи булева линейного программирования (6)—(8). Целевая функция
нижней задачи получается из целевой функции интервальной задачи (6) заменой интервальных
коэффициентов ![]() - их нижними границами ci1, а целевая функция верхней
задачи — из той же целевой функции (6) заменой коэффициентов
- их нижними границами ci1, а целевая функция верхней
задачи — из той же целевой функции (6) заменой коэффициентов ![]() их верхними
границами ci2. Система
ограничений нижней и верхней граничных задач одна и та же; она образуется
соединением двух систем ограничений — первой, полученной из системы ограничений
интервальной задачи (7) заменой интервальных коэффициентов
их верхними
границами ci2. Система
ограничений нижней и верхней граничных задач одна и та же; она образуется
соединением двух систем ограничений — первой, полученной из системы ограничений
интервальной задачи (7) заменой интервальных коэффициентов ![]() и интервальных свободных
членов
и интервальных свободных
членов ![]() их
нижними границами aij1 и bi1, и второй, полученной из той же
системы (7) заменой коэффициентов
их
нижними границами aij1 и bi1, и второй, полученной из той же
системы (7) заменой коэффициентов ![]() и свободных членов
и свободных членов ![]() их верхними
границами aij2 и bi2. В число ограничений нижней и
верхней граничных задач включаются также требование булевости переменных (8).
их верхними
границами aij2 и bi2. В число ограничений нижней и
верхней граничных задач включаются также требование булевости переменных (8).
Шаг 2. Нахождение множества решений МH нижней граничной задачи. Для этого можно использовать любые известные методы решения обычной (детерминированной) задачи булева линейного программирования: прямой поиск, фильтрующий поиск, перебор по Балашу и т. д. [3].
Шаг 3. Нахождение множества решений МB верхней граничной задачи с использованием тех же методов, что и на шаге 2.
Шаг 4. Нахождение пересечения М множеств МH и МB, для чего перебираются элементы одного множества и помечаются те из них, которые входят во второе множество. Если М ≠ Ø, то любой элемент-решение из М есть решение имеющейся интервальной задачи булева линейного программирования. Если же М = Ø, то данная задача не имеет решения.
При большой размерности задачи полезна такая следующая теорема.
Теорема 6. Если множества решений нижней МH и верхней МB
граничных задач пересекаются, образуя непустое множество решений М = МH ![]() МB
интервальной задачи (б)—(8), то это же множество решений М имеет обычная
(детерминированная) задача булева линейного программирования с целевой функцией
МB
интервальной задачи (б)—(8), то это же множество решений М имеет обычная
(детерминированная) задача булева линейного программирования с целевой функцией
Q(X) = aQ1(X) + (1-a) Q2(X), 0 ≤ a≤ 1, (9)
и теми же ограничениями, что и обе граничные задачи.
Из теоремы 6 следует, что для нахождения множества решений М задачи (6)—(8) при больших n можно поступить следующим образом. Сначала подбором коэффициента а (a ≈ 1 и a ≈ 0) настроить задачу с целевой функцией Q(X) (6) на близкие к граничным задачи с целевыми функциями, близкими к Q1(X) и Q2(X), и найти множества их решений МH и МB. Если МH = МB = М (непустое множество), то М и есть искомое множество решений задачи (6)—(8). Если же МH = МB = Ø (пустое множество), то задача (6)—(8) не имеет решений.
Задача составления расписания
В качестве третьего примера рассмотрим задачи теории расписаний и на примере простейшей задачи трех станков покажем путь развития недетерминистской (интервальной) теории расписаний.
Интервальная задача трех станков заключается в выборе оптимального
расписания (порядка) подачи n деталей на
конвейер из трех последовательных станков в предположении, что время обработки
любой i-й детали на 1-м, 2-м и 3-м станках равно
соответствующим интервальным величинам ![]() . Предполагается,
что очередная деталь подается на 1-й станок сразу после его освобождения от
предыдущей детали, а на 2-й (3-й) станок — сразу после ее обработки на 1-м
(2-м) станке и освобождения 2-го (3-го) станка от предыдущей детали.
. Предполагается,
что очередная деталь подается на 1-й станок сразу после его освобождения от
предыдущей детали, а на 2-й (3-й) станок — сразу после ее обработки на 1-м
(2-м) станке и освобождения 2-го (3-го) станка от предыдущей детали.
Используем принятые в теории расписаний методы, учтя особенности сравнения интервальных величин и выделения экстремальной величины. Введем понятия нижней и верхней граничных детерминированных задач трех станков (в 1-й время обработки любой i-й детали на 1-м, 2-м и 3-м станках равно нижним границам ai1, bi1 и ci1 времени обработки этих деталей в заданной интервальной системе, во 2-й — верхним границам ai2, bi2, ci2 этого времени). Тогда основной результат можно сформулировать в следующем виде [6].
Теорема 7. Для того чтобы в интервальной задаче трех станков с
временем обработки на 1-м, 2-м и 3-м станках деталей i
в виде интервалов ![]() некоторая перестановка
деталей Рn = (i1,...,
in) была оптимальной
последовательностью обработки, достаточно, чтобы Рn была оптимальной последовательностью обработки
деталей в ее нижней и верхней граничных задачах.
некоторая перестановка
деталей Рn = (i1,...,
in) была оптимальной
последовательностью обработки, достаточно, чтобы Рn была оптимальной последовательностью обработки
деталей в ее нижней и верхней граничных задачах.
Теорема 8. Множество М всех оптимальных последовательностей
обработки деталей в интервальной задаче трех станков с временем обработки
деталеи i на 1-м, 2-м и 3-м станках в виде
интервалов ![]() равно пересечению множеств
МH и МB
всех оптимальных последовательностей обработки деталей в ее нижней и верхней
граничных задачах.
равно пересечению множеств
МH и МB
всех оптимальных последовательностей обработки деталей в ее нижней и верхней
граничных задачах.
Теоремы 7 и 8 сводят решение интервальной задачи составления оптимальных расписаний к решению двух детерминированных задач составления расписаний.
Алгоритм решения выглядит таким образом.
Шаг 1. Отыскание множества МH всех оптимальных последовательностей подачи n деталей в нижней граничной задаче имеющейся интервальной задачи трех станков со следующим временем обработки i-й детали на 1-м, 2-м и 3-м станках: ai = ai1, bi = bi1, ci = ci1. Для этого можно использовать любые известные методы решения детерминированной трехстадийной задачи теории расписаний [7—9].
Шаг 2. Отыскание множества МB всех оптимальных последовательностей подачи п деталей в верхней граничной задаче имеющейся интервальной задачи трех станков с временем обработки i-й детали на 1-м, 2-м и 3-м станках ai = ai2, bi = bi2, ci = ci2 с использованием тех же методов, что и на шаге 1.
Шаг 3. Нахождение пересечения М множеств МH и МB, для чего перебирают элементы одного множества и помечают те из них, которые входят во второе множество. Если М ≠ Ø, то любая последовательность деталей из М есть искомая оптимальная последовательность подачи n деталей на конвейер из трех последовательных станков с интервально заданным временем обработки деталей. Если М = Ø, то таких последовательностей не существует, т. е. поставленная задача об оптимальном расписании обработки деталей не имеет решения.
Примеры
Рассмотрим некоторые примеры решения задач оптимизации с интервальными параметрами.
Пример 1. Решим недетерминированную задачу о назначениях с тремя должностями и тремя претендентами с интервальной матрицей издержек

Шаг 1. Найдем множество решений МH
нижней граничной задачи. Матрица издержек этой задачи А1.
Используем метод логических определителей [2]. Логическим определителем ![]() ,
, ![]() произвольной
квадратной матрицы А =
произвольной
квадратной матрицы А = ![]() называется минимальная
(максимальная) из сумм ее элементов, включающая каждая ровно по одному элементу
из любой строки и любого столбца. Эти
называется минимальная
(максимальная) из сумм ее элементов, включающая каждая ровно по одному элементу
из любой строки и любого столбца. Эти
суммы
обозначаются ![]() . Таким образом
. Таким образом
![]() (10)
(10)
Нетрудно понять, что каждая сумма вида ![]() определяет некоторое
распределение должности между претендентами в детерминированной задаче о
назначениях с матрицей издержек А =
определяет некоторое
распределение должности между претендентами в детерминированной задаче о
назначениях с матрицей издержек А = ![]() : включение в сумму элемента aij - означает
назначение i-го претендента на j-ю должность. Поэтому решение детерминированной задачи о
назначениях с матрицей издержек А эквивалентно вычислению логического
определителя
: включение в сумму элемента aij - означает
назначение i-го претендента на j-ю должность. Поэтому решение детерминированной задачи о
назначениях с матрицей издержек А эквивалентно вычислению логического
определителя ![]() ,
более точно — отысканию значения и поэлементного состава минимальной суммы
,
более точно — отысканию значения и поэлементного состава минимальной суммы
![]() , которой равен
наш определитель
, которой равен
наш определитель ![]() . Вычисляется определитель путем
его последовательного разложения по формуле [9]
. Вычисляется определитель путем
его последовательного разложения по формуле [9]
![]() (11)
(11)
где ![]() — логическое
дополнение элемента aij в
— логическое
дополнение элемента aij в ![]() , т. е.
определитель, полученный из
, т. е.
определитель, полученный из ![]() вычеркиванием i-й строки и j-го столбца,
на пересечении которых стоит aij.
Вышеописанной формуле соответствует дерево последовательного разложения
определителя
вычеркиванием i-й строки и j-го столбца,
на пересечении которых стоит aij.
Вышеописанной формуле соответствует дерево последовательного разложения
определителя ![]() ,
и вычисление
,
и вычисление ![]() означает
определение длины кратчайшего пути из корня дерева в висячую вершину и
идентификацию этого пути по составу входящих в него вершин-элементов aij. Дерево разложения логического
определителя
означает
определение длины кратчайшего пути из корня дерева в висячую вершину и
идентификацию этого пути по составу входящих в него вершин-элементов aij. Дерево разложения логического
определителя ![]() ,
дающее решение нижней граничной задачи с матрицей издержек А1
согласно формуле (11) имеет вид, представленный на рисунке. В этом дереве есть
четыре минимальных пути из корня в висячую вершину (выделены жирно), имеющих
одинаковую длину, равную 5. Им соответствуют четыре минимальные суммы
,
дающее решение нижней граничной задачи с матрицей издержек А1
согласно формуле (11) имеет вид, представленный на рисунке. В этом дереве есть
четыре минимальных пути из корня в висячую вершину (выделены жирно), имеющих
одинаковую длину, равную 5. Им соответствуют четыре минимальные суммы ![]() - матрицы А1,
а именно: a11 + a22
+ a33 = 5, a11
+ a23 + a32
= 5, a12 + a21
+ a33 = 5, a13
+ a21 + a32
= 5, дающие четыре решения задачи в виде четырех матриц назначения. В итоге
получаем множество решений МH нижней
граничной задачи
- матрицы А1,
а именно: a11 + a22
+ a33 = 5, a11
+ a23 + a32
= 5, a12 + a21
+ a33 = 5, a13
+ a21 + a32
= 5, дающие четыре решения задачи в виде четырех матриц назначения. В итоге
получаем множество решений МH нижней
граничной задачи
MH = {X1,…, X4},
где
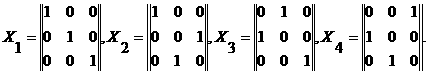

Дерево разложения логического определителя нижней граничной задачи
Шаг 2. Таким же способом находим множество решений МB верхней граничной задачи с матрицей издержек А2
МB = {Х5, Х6},
где

Шаг 3. Пересечение множеств МH и МB состоит из одной матрицы назначения
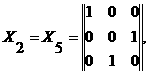
которая и есть решение всей задачи. Согласно этому решению 1-я должность отдается 1-му претенденту, а 2-я и 3-я — соответственно 3-му и 2-му претендентам.
Пример 2. Решим недетерминированную задачу булева линейного программирования с интервальными коэффициентами

x1, x2, x3 = 0 или 1.
Здесь коэффициенты — следующие интервалы: ![]() = [1, 2],
= [1, 2], ![]() = [2, 4],
= [2, 4], ![]() = [1, 3],
= [1, 3], ![]() = [0, 1],
= [0, 1], ![]() = [1, 3],
= [1, 3], ![]() = [2, 3],
= [2, 3], ![]() = [1, 3],
= [1, 3], ![]() = [1, 2],
= [1, 2], ![]() = [0, 4],
= [0, 4], ![]() = [2, 5],
= [2, 5], ![]() = [3, 7].
= [3, 7].
Шаг 1. Формируем нижнюю и верхнюю граничные задачи имеющейся интервальной задачи. Нижняя граничная задача
Q1(x) = x1 + 2x2 + x3 = max;
x2 + 2x3 ≤ 2; (a)
x1 + x2 ≤ 3; (b)
x1 + 3x2+3x3 ≤ 5; (c)
3x1 + 2x2 + 4x3 ≤7; (d)
x1, x2,
x3 ![]() {0,1}.
{0,1}.
Верхняя граничная задача
Q2(x) = 2х1 + 4х2 + Зх3 = max,
ограничения те же.
Шаг 2. Находим множество решений МH нижней граничной задачи. Используем фильтрующий поиск [3]. Сразу видим одно допустимое решение x = (х, х2, х3) = (110), удовлетворяющее всем ограничениям (a) - (d). Для него значение целевой функции Q1(x) = 3. Это дает дополнительное, фильтрующее ограничение
x1 + 2x2 + x3 ≥ 3. (e)
Строим таблицу поиска, располагая в ней векторы неизвестных x в лексикографическом порядке. В таблицу не включаем ограничение (b), которое заведомо выполняется для любых x.
|
Вектор неизве-стных |
Левая часть ограничений |
Выполнение системы ограничений |
Значение целевой функции |
|||
|
1 |
3 |
4 |
5 |
|||
|
000 |
|
|
|
0 |
Нет |
|
|
001 |
|
|
|
1 |
Нет |
|
|
010 |
|
|
|
2 |
Нет |
|
|
011 |
|
6 |
6 |
3 |
Нет |
|
|
100 |
|
|
|
1 |
Нет |
|
|
101 |
|
|
|
2 |
Нет |
|
|
110 |
2 |
4 |
5 |
3 |
Да |
3 |
|
111 |
|
|
9 |
4 |
Нет |
|
Выполнение остальных ограничений проверяем в порядке убывания их номера. Проверку прекращаем, как только выявлено невыполнение какого-либо ограничения. Для векторов ч, удовлетворяющих всем ограничениям, вычисляем значение целевой функции Q1(x). Из заполненной таблицы видно, что есть лишь одно допустимое решение x = (110) со значением целевой функции Q1(x) = 3, т. е. единственное решение нижней граничной задачи x* = (110), соответствующее максимуму целевой функции Q1(x*) = 3.
Шаг 3. Находим множество решений МB верхней граничной задачи. Действуя аналогично предыдущему, получаем единственное решение x** = (110), которому соответствует максимум целевой функции Q2(x**) = 6.
Шаг 4. Пересечение множеств МH
и МB дает единственное решение
заданной интервальной задачи булева линейного программирования x = x* = x** = (110). Этому решению соответствует следующий
интервальный максимум целевой функции задачи: ![]() = [1, 2] • 1 + [2, 4] • 1 + [1,
3] • 0 = [3, 6].
= [1, 2] • 1 + [2, 4] • 1 + [1,
3] • 0 = [3, 6].
Список литературы
1. Левин В. И. Сравнение интервальных величин и оптимизация неопределенных систем // Информационные технологии. 1998. № 7. С. 22-32.
2. Левин В. И. Дискретная оптимизация в условиях интервальной неопределенности // Автоматика и телемеханика. 1992. № 7. С. 97—106.
3. Кофман А., Анри-Лабордер А. Методы и модели исследования операций. Целочисленное программирование. М.: Мир, 1997. 423 с.
4. Растригин Л. А. Статистические методы поиска. М.: Наука, 1968. 320 с.
5. Левин В. И. Булево линейное программирование с интервальными коэффициентами // Автоматика и телемеханика. 1994. №7. С. 111-122.
6. Левин В. И. Задача трех станков с неопределенными временами обработки // Автоматика и телемеханика. 1996. № 1. С. 109-120.
7. Конвей Р. В., Максвелл В. Л., Миллер Л. В. Теория расписаний. М.: Наука. 1975. 360 с.
8. Танаев В. С, Шкурба В. В. Введение в теорию расписаний. М.: Наука. 1975. 256 с.
9. Левин В. И. Структурно-логические методы исследования сложных систем с применением ЭВМ. М.: Наука, 1987. 304 с.
МЕТОДЫ ОПТИМИЗАЦИИ
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 1, 1999
Ключевые слова: Двоичное линейное программирование, дискретная интервальная оптимизация, экстремальные интервалы, распределение ограниченных ресурсов.
Публикации с ключевыми словами: распределение ограниченных ресурсов, Двоичное линейное программирование, дискретная интервальная оптимизация, экстремальные интервалы
Публикации со словами: распределение ограниченных ресурсов, Двоичное линейное программирование, дискретная интервальная оптимизация, экстремальные интервалы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



