научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2013
DOI: 10.7463/0413.0554360
УДК 519.6
Россия, Физический институт им. П.Н. Лебедева РАН (ФИАН). Астрокосмический центр
Россия, МГТУ им. Н.Э. Баумана
Россия, КФ МГТУ им. Н.Э. Баумана
Данная работа является второй в серии из четырех публикаций, посвященных синтезу механизмов ориентации космического телескопа «Миллиметрон» [1].
Синтез манипуляционного робота, построенного на основе механизмов параллельной структуры типа гексапод (платформа Стюарта), для управления ориентацией космического телескопа «Миллиметрон» требует решения целого комплекса сложных плохоформализованных задач. Для решения этих задач целесообразна разработка специализированной программной системы автоматизированного проектирования. В работе предложена структура такой программной системы и разработан прототип ее основной подсистемы – подсистемы автоматизированного структурного синтеза. Разработанное программное приложение формирует требуемое проектное решение в виде трехмерной параметризованной компоновочной модели в CAD-системе SolidWorks, а также в пакете MatLab Simulink. С помощью указанного приложения выполнено исследование моделей нескольких манипуляторов.
Поскольку реализация манипулятора «в железе» отсутствует, возникает проблема проверки адекватности указанной выше SolidWorks-модели. С этой целью разработана 3D геометрическая модель манипулятора, построенная средствами «тяжелой» графической системы NX .5 и её приложения «Симуляция кинематических механизмов». С помощью данной модели подтверждена адекватность указанной модели манипулятора.
Самостоятельной сложной задачей является планирование траекторий перевода антенны телескопа из текущего в заданное допустимое положение. Для решения этой задачи разработано программное приложение, предназначенное для решения прямой и обратной задач позиционирования многосекционного манипулятора. С помощью данного программного обеспечения построены траектории перемещения антенны, которые оставляют неподвижным центр масс системы антенна ‑ криоконтейнер.
Проектирование мносекционного манипулятора для управления антенной телескопа требует решения также комплекса задач по разработке системы автоматического управления (САУ) таким манипулятором. Первая из задач, которые нужно при этом решить, состоит в выборе и обосновании парадигмы (классические САУ, адаптивные САУ, нейросетевые САУ и т.д.), в рамках которой следует строить такую систему. Для исследования возможности использования классических САУ средствами системы MatLab Simulink построена модель пятисекционного управляемого манипулятора. С помощью модели выполнено исследование кинематики и динамики переходных процессов в манипуляторе при переводе его из транспортного в рабочее положение, а также АЧХ и ФЧХ системы управления манипулятором.
В работе дана постановка задачи ориентации антенны радиотелескопа «Миллиметрон» с помощью многосекционного манипулятора, построенного на основе механизма параллельной кинематики типа гексапод. Рассмотрена задача синтеза манипулятора средствами системы Solid Works. Представлена 3D геометрическая модель манипулятора, построенная средствами «тяжелой» графической системы NX .5 и её приложения «Симуляция кинематических механизмов». Разработано программное приложение, предназначенное для решения прямой и обратной задач позиционирования многосекционного манипулятора. Представлена модель пятисекционного управляемого манипулятора, построенная средствами системы MatLab Simulink.
2.1. Постановка задачи
Исходные данные:
· максимально допустимый диаметр секций манипулятора – 3640 мм;
· диаметр антенны телескопа – 10 000 мм;
· суммарная масса антенны телескопа и криоконтейнера – 2500 кг;
· центр масс системы антенна телескопа ‑ криоконтейнер находится на расстоянии 2200 мм от основания криоконтейнера, т.е. от последней платформы манипулятора;
· секции манипулятора представляют собой механизмы параллельной кинематики типа гексапод;
· платформы гексаподов изготавливаются в виде равносторонних треугольников со срезанными вершинами из трубчатого углепластика прямоугольного сечения ![]() мм, имеющего плотность 1550 кг/м3;
мм, имеющего плотность 1550 кг/м3;
· штанги гексаподов могут быть двух- и трехсоставными (т.е. могут состоять из двух или трех полуштанг) и изготавливаются также из указанного углепластика;
· в сложенном состоянии манипулятор должен вписываться в цилиндр высотой 750 мм и диаметром 3640 мм.
Центр масс системы антенна телескопа ‑ криоконтейнер для простоты записи называем далее схватом манипулятора.
Манипулятор должен обеспечивать ориентацию антенны телескопа в пределах полусферы, ось симметрии которой совпадает с продольной осью симметрии манипулятора (и космического летательного аппарата в целом). Во всех случаях, антенна телескопа должна отстоять от первой платформы манипулятора не менее чем на 5000 мм.
2.2. Синтез манипулятора средствами Solid Works
В силу значительной кинематической сложности даже односекционных параллельных механизмов, для 3D моделирования, анализа и синтеза многосекционного манипулятора возможно использование только систем среднего класса типа Inventor, Solid Works, Solid Edge, КОМПАС и «тяжелых» систем типа CATIA, UNIGRAPHICS, Pro-Engineer [2]. В данном разделе рассматриваем использование системы Solid Works.
2.2.1. Программное приложение
Для построения 3D-модели многосекционного манипулятора в программной среде .NET разработано соответствующее приложение. В качестве инструмента для написания программы использована среда разработки Microsoft Visual Studio 2010. Приложение является одним из модулей разрабатываемой авторами системы поддержки принятия решений (СППР), предназначенной для проектирования многосекционных манипуляторов параллельной структуры. Приложение в автоматизированном режиме выполняет следующие действия:
- принимает параметры манипулятора, передаваемые в виде текстового файла;
- выводит на экранную форму древовидную структуру манипулятора с указанием всех его параметров и возможностью изменения этих параметров пользователем;
- осуществляет построение параметрической 3D-модели манипулятора средствами системы SolidWorks API [3].
Основной частью приложения является объектная модель манипулятора. Диаграмма классов, использованных при создании этой модели, представлена на рисунке 2.1.
Рисунок 2.1 показыает, что каждому конструктивному элементу манипулятора (штанга, шарнир и др.) поставлен в соответсвие програмный объект, описывающий основные его свойства. Таким образом, модель манипулятора представляет собой иерархию объектов типа «секция», «штанга», «шарнир», «платформа».
Вид главного окна приложения представлен на рисунке 2.2.
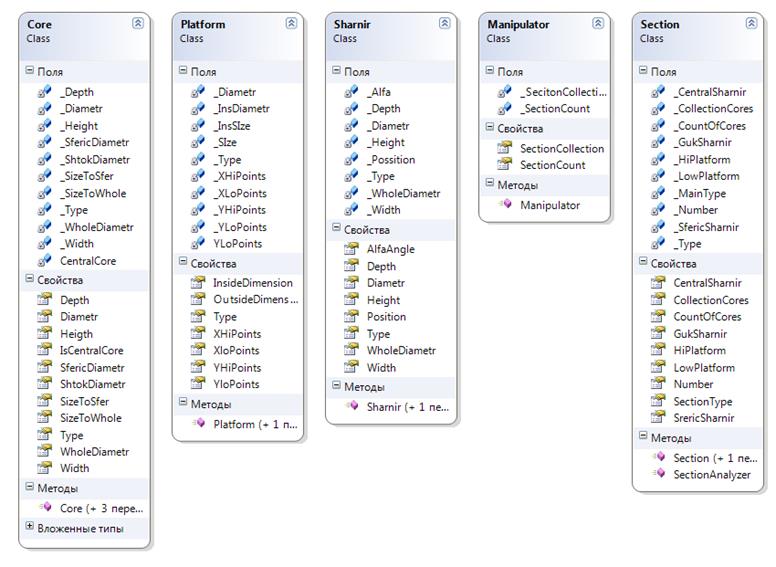
Рисунок 2.1 – Объектная модель манипулятора
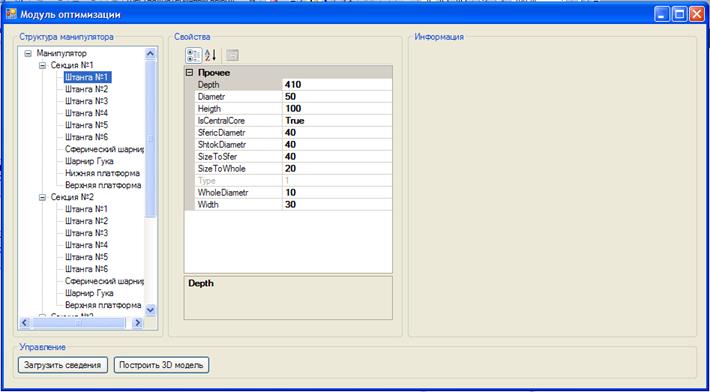
Рисунок 2.2 - Главное окно приложения
Для функционирования приложения необходимы следующие ресурсы:
- операционная система Microsoft® Windows Vista® (SP1 или SP2) либо Windows® XP Professional (SP2 или SP3);
- процессор Intel® Pentium® 4 с тактовой частотой 2 ГГц или выше, либо процессоры Intel® Xeon™, Intel® Core™, AMD Athlon™ 64, AMD Opteron™ и выше;
- не менее 2 Гб оперативной памяти;
- графический адаптер, поддерживающий Direct 3D 10, Direct 3D 9 или Open GL;
- Microsoft .NET Framework 3 или более поздняя версия;
- Solid Works 2012.
С помощью рассматриваемого приложения разработаны четыре параметризованных модели манипулятора:
‑ манипулятор 11 (все платформы одинаковы, штанги являются двухсоставными);
‑ манипулятор 12 (все платформы одинаковы, штанги являются трехсоставными);
‑ манипулятора 21 (промежуточные платформы имеют меньшие размеры, штанги являются двухсоставными);
‑ манипулятора 22 (промежуточные платформы имеют меньшие размеры, штанги являются трехсоставными).
Параметризация модели позволяет, в частности, менять число платформ манипулятора. Пример визуализации Solid Works модели манипулятора 11 представлен на рисунке 2.3.

Рисунок 2.3 – Пример 3DSolidWorksмодели пятисекционного манипулятора 11
2.2.2. Solid Works модель манипулятора 1
Модели платформы и компонентов двухсоставной штанги для манипулятора 1 представлены на рисунках 2.4, 2.5, а аналогичные модели трехсоставной штанги – на рисунке 2.6. Во всех случаях длины штанг определены из условия возможности складывания манипулятора в транспортное положение. Заметим, что поскольку речь идет о геометрической модели манипулятора, эта модель не включает в себя модели приводов штанг.
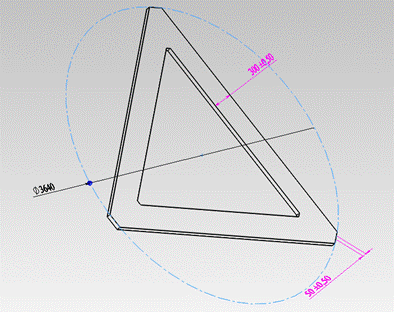
Рисунок 2.4 – SolidWorksмодель платформы для манипулятора 1

а) шток
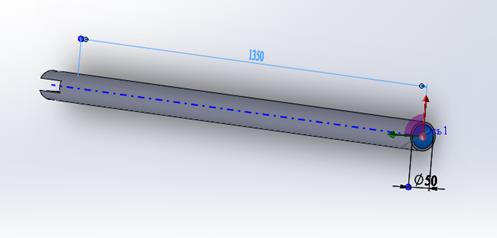
б) стакан

в) штанга в сборе
Рисунок 2.5 – SolidWorksмодель двухсоставной штанги для манипулятора 1

а) шток
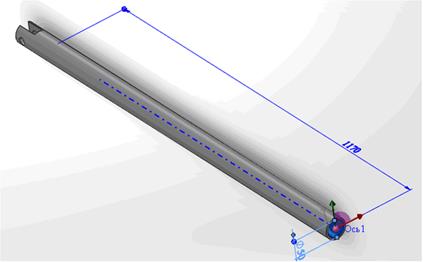
б) стакан 1

в) стакан 2
Рисунок 2.6 – SolidWorksмодель трехсоставной штанги для манипулятора 1
Модель пятисекционного манипулятора 11 в сложенном, развернутом и максимально наклоненном положениях иллюстрирует рисунок 2.7. Рисунок показывает, что пятисекционный манипулятор, построенный из секций одинакового размера с использованием двухсоставных штанг, не позволяет перевести антенну телескопа в положение, в котором ее ось симметрии перпендикулярна продольной оси симметрии манипулятора.
Манипулятор с числом секций, большим пяти, не рассматривался в силу его высокой кинематической сложности, которую Solid Works не всегда способен поддержать.

а) сложенное положение
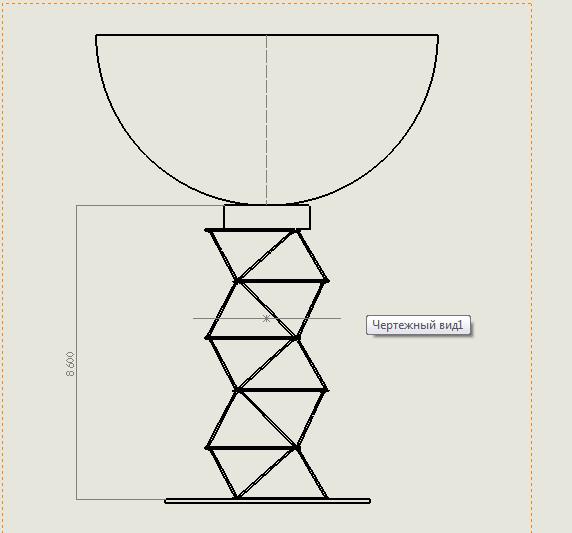
б) развернутое положение

в) максимально возможный наклон
Рисунок 2.7 – SolidWorksмодель манипулятора 11
Модель манипулятора 12 в положении максимально возможного наклона антенны представлена на рисунке 2.8.
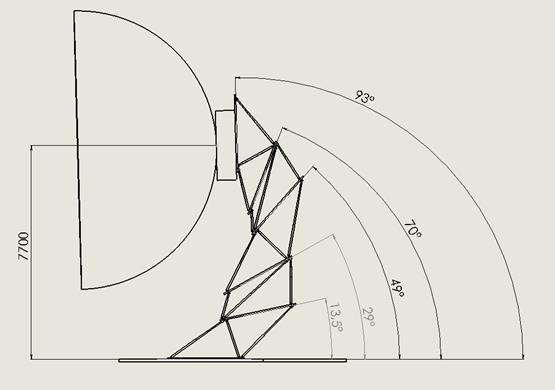
Рисунок 2.8 – SolidWorksмодель манипулятора 12: максимально возможный наклон антенны
Рисунок 2.8 показывает, что манипулятор 12 позволяет выполнить ориентацию оси симметрии антенны телескопа перпендикулярно продольной оси манипулятора.
2.2.3. Solid Works модель манипулятора 2
С помощью Solid Works модели манипулятора 2 выполнен синтез пятисекционного манипулятора при следующих соглашениях:
‑ размеры первой и последней платформ манипулятора совпадают с размерами платформ манипулятора 1 (п. 2.2.2);
‑ размеры промежуточных платформ одинаковы.
Как и в предыдущем разделе данная модель манипулятора не включает в себя модели приводов штанг. Ставилась задача найти максимально возможный диаметр промежуточных платформ, обеспечивающий ориентацию оси симметрии антенны телескопа перпендикулярно продольной оси манипулятора.
Методом перебора диметров промежуточных платформ установлено, что пятисекционный манипулятор 21 способен решить поставленную задачу. Различные положения синтезированного манипулятора 21 иллюстрирует рисунок 2.9. Поскольку конструктивно более простой манипулятор 21 решает поставленную задачу, манипулятор 22 не исследовался.

а) сложенное положение
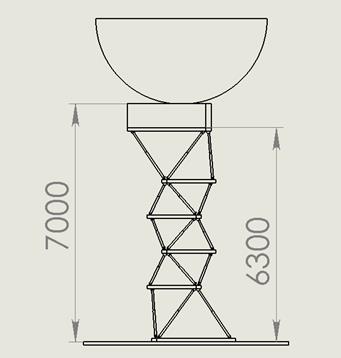
б) развернутое положение

Рисунок 2.9 – SolidWorksмодель манипулятора 21: угол наклона антенны равен 90![]()
2.3. Синтез манипулятора средствами системы NX 7.5
Основной целью данного пункта является построение 3Dгеометрической модели манипулятора средствами «тяжелой» графической системы NX 7.5 и её приложения «Симуляция кинематических механизмов» [4]. Данная модель призвана подтвердить адекватность моделей манипулятора, рассмотренных в п. 2.2. В терминах этого пункта, рассматриваем только модель пятисекционного манипулятора 11. Подобно п. 2.2, поскольку речь идет о геометрической модели манипулятора, разработанная модель не включает в себя модели приводов штанг.
2.3.1. Модель секции манипулятора 11
Секция манипулятора 11 представляет собой две треугольные платформы, соединенные между собой шестью двухсоставными телескопическими штангами (рисунок 2.10).

Рисунок 2.10 – NXмодель секции манипулятора 11 (произвольное положение платформы)
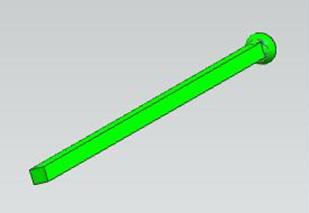
Каждая из телескопических штанг секции состоит из стакана и подвижного штока (рисунок 2.11).

а) б)
Рисунок 2.11 – NXмодель стакана (а) и штока (б) двухсоставной штанги манипулятора 11
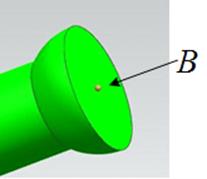
Полагаем, что шток может выдвинуться из стакана не более чем на 2\3 от общей своей длины. При этом минимальная и максимальная длины штанги равны 1300 мм и 2000 мм соответственно. Каждая из штанг крепится к основанию (нижней платформе) с помощью шарнира Гука, а к (верхней) платформе – с помощью сферического шарнира. Модель шарнира Гука представлена на рисунке 2.12а.


а) б) в)
Рисунок 2.12 – NXмодель шарнира Гука
При исследовании кинематики манипулятора необходимо измерять длину частично или полностью раздвинутой штанги. Эта длина измеряется от центра шарнира Гука (точка А на рисунке 2.12б) до центра сферического шарнира (точка B на рисунке 2.12в).
Вершины платформ манипулятора нумеруем цифрами от 1 до 3 против часовой стрелки. Для того, чтобы однозначно идентифицировать номера углов, каждый из углов помечен соответствующим числом красных точек (рисунок 2.13). Схему соединения платформ иллюстрирует рисунок 2.14.
Штанги секций нумеруем двумя цифрами - первая цифра обозначает номер угла основания (нижней платформы), к которому прикреплена штанга, вторая цифра обозначает номер угла верхней платформы, к которому прикреплена та же штанга.

Рисунок 2.13 – К нумерации углов платформ

Рисунок 2.14 – Схема соединения платформ штангами
Основные конструктивные размеры платформы показаны на рисунке 2.15. Осевые линии мест крепления шарниров Гука и сферических шарниров совпадают (рисунки 2.16, 2.17). На рисунке 2.16 показан вид сверху на один из углов платформы. Два отверстия рядом с красными точками представляют собой посадочные места для шарниров Гука. Вид снизу на тот же угол платформы показан на рисунке 2.17. Внутри посадочных мест для сферических шарниров видны отверстия для шарниров Гука. Размеры, определяющие точные положения указанных отверстий, показаны на рисунке 2.18.
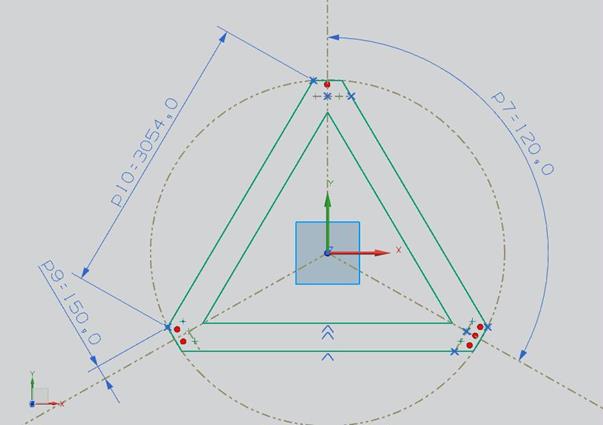
Рисунок 2.15 – Основные размеры платформы
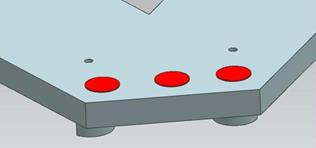
Рисунок 2.16 - Вид сверху на один из углов платформы

Рисунок 2.17 - Вид снизу на один из углов платформы

Рисунок 2.18 – Положения отверстий для установки шарниров Гука
2.3.2. Модель манипулятора 11
На представленных ниже рисунках показаны начальное, конечное и три промежуточных положений манипулятора 11 при переводе его из исходного сложенного состояние в состояние, в котором ось симметрии антенны телескопа перпендикулярна продольной оси симметрии манипулятора. Указанная эволюция манипулятора осуществляется таким образом, что центр масс антенны ![]() движется в плоскости
движется в плоскости ![]() (рисунок 2.19а). В подрисуночных надписях приведены соответствующие координаты точки
(рисунок 2.19а). В подрисуночных надписях приведены соответствующие координаты точки ![]() (в миллиметрах).
(в миллиметрах).
Перевод манипулятора из начального в конечное положение выполняется за 200 шагов. На рисунка, иллюстрирующих промежуточные положения манипулятора, указаны соответствующие числа шагов.
Обратим внимание на разрывы штанг на рисунке 2.19 д во всех секциях, кроме последней секции. Эти разрывы свидетельствуют о том, что обеспечить требуемый поворот антенны с помощью манипулятора 11 с двухсоставными штангами не удается. В то же время, недостаток длин штанг невелик и может быть покрыт трехсоставными штангами.

а) Начальное положение манипулятора: ![]()
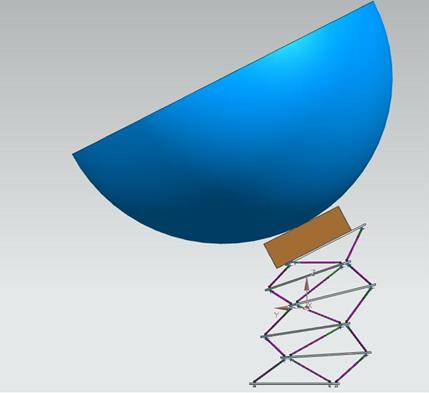
б) Промежуточное положение манипулятора: число шагов равно 50; ![]()
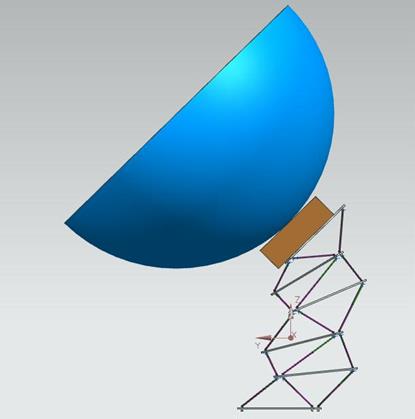
в) Промежуточное положение манипулятора: число шагов равно 100; ![]()

г) Промежуточное положение манипулятора: число шагов равно 150; ![]()
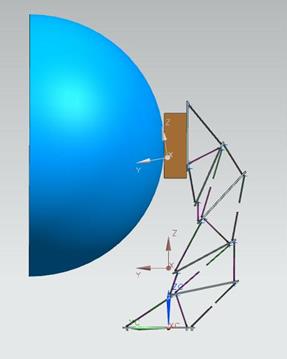
д) Конечное положение манипулятора: ![]()
Рисунок 2.19 – Эволюция манипулятора 11
2.3.3. Расстояние между платформами в функции длины штанг
С помощью представленной выше модели манипулятора 11 выполнено исследование зависимости расстояния между платформами Hсекции манипулятора от длины штанг L(таблица 2.1). В таблице принято, что длины Lвсех шести штанг меняются одновременно и синхронно.
Из таблицы 2.1 следует, что для того чтобы поднять платформу из сложенного состояния на 100 мм, длины штанг нужно не увеличивать, а наоборот уменьшать (хотя и не намного – всего, примерно, на 3 мм). Таким образом, при проектировании одноразового устройства, которое обеспечивает перевод манипулятора в рабочее положение (когда начинают нормально функционировать двигатели его приводов) следует учитывать данное обстоятельство.
Отметим также, что, как следует из той же таблицы, для увеличения расстояния между платформами со 100 мм до 300 мм, штанги нужно удлинить всего на 15 мм.
Таблица 2.1 – Длины тяг Lв функции расстояния H
Расстояние H, мм | Длина тяг L (мм) |
0 | 1467.86 |
10 | 1467.2 |
20 | 1466.7 |
50 | 1465.47 |
70 | 1464.995 |
100 | 1464.79 |
11 | 1464.86 |
120 | 1464.995 |
130 | 1465.2 |
140 | 1465.47 |
150 | 1465.81 |
170 | 1466.7 |
200 | 1468.54 |
250 | 1472.96 |
300 | 1479.05 |
350 | 1486.81 |
400 | 1496.199 |
450 | 1507.19 |
500 | 1519.74 |
550 | 1533.82 |
600 | 1549.39 |
650 | 1566.4 |
700 | 1580.89 |
800 | 1625.6 |
900 | 1714.6 |
1200 | 1834.8 |
1400 | 1961 |
1600 | 2100 |
2.4. Синтез траекторий перевода манипулятора в заданное положение
Для синтеза траекторий перевода манипулятора из заданного в требуемое конечное положение разработано программное приложение. Разработка выполнена на языке С++, при разработке использованы кроссплатформенные библиотеки Qt (интерфейс диалогового окна программы) и OpenGL (визуализация манипулятора). Приложение написано в соответствии с идеями объектно-ориентированного программирования и состоит из набора классов, иерархически связанных между собой. Основное диалоговое окно приложения представлено на рисунке 2.20.

Рисунок 2.20 – Основное диалоговое окно программного приложения
Приложение использует решение прямой и обратной задач кинематики манипулятора. Рассмотрим используемые в приложении алгоритмы решения этих задач.
2.4.1. Прямая позиционная задача
Для рассматриваемого манипулятора прямой позиционной задачей называется задача определения положения и, быть может, ориентации схвата манипулятора при заданных значениях длин всех его штанг.
Свяжем с ![]() -ой секцией манипулятора систему координат
-ой секцией манипулятора систему координат ![]() , в которой ось
, в которой ось ![]() совпадает с продольной осью симметрии этой секции, а оси
совпадает с продольной осью симметрии этой секции, а оси ![]() ,
, ![]() расположены таким образом, что образуют с осью
расположены таким образом, что образуют с осью ![]() правую тройку (рисунок 2.21). Систему координат, связанную с основанием манипулятора, обозначим
правую тройку (рисунок 2.21). Систему координат, связанную с основанием манипулятора, обозначим ![]() .
.
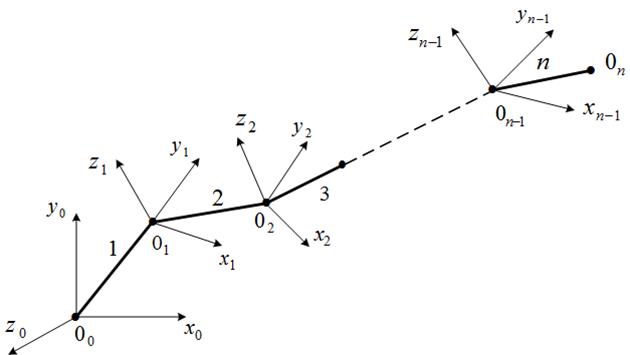
1, 2, …, n – номера секций; ![]() – схват манипулятора
– схват манипулятора
Рисунок 2.21 - Системы координат манипулятора
Введем следующие обозначения [5]: ![]() ,
, ![]() - однородная
- однородная ![]() -матрица, задающая переход от системы координат
-матрица, задающая переход от системы координат ![]() к системе координат
к системе координат ![]() ;
; ![]() - вектор обобщенных координат
- вектор обобщенных координат ![]() -ой секции манипулятора (в нашем случае – шестимерный вектор длин штанг гексапода, на основе которого построена данная секция);
-ой секции манипулятора (в нашем случае – шестимерный вектор длин штанг гексапода, на основе которого построена данная секция); ![]() - вектор обобщенных координат
- вектор обобщенных координат ![]() -секционного манипулятора;
-секционного манипулятора; ![]() -
- ![]() однородная матрица, определяющая положение системы координат
однородная матрица, определяющая положение системы координат ![]() в системе координат
в системе координат ![]() ;
; ![]() -
- ![]() обобщенный вектор положения характерной точки рабочего органа
обобщенный вектор положения характерной точки рабочего органа ![]() в системе координат
в системе координат ![]() ;
; ![]() -
- ![]() аналогичный вектор положения схвата
аналогичный вектор положения схвата ![]() в системе координат
в системе координат ![]() .
.
Во введенных обозначениях имеем
![]() , (2.1)
, (2.1)
где ![]() ;
; ![]() - совокупность допустимых значений вектора обобщенных координат
- совокупность допустимых значений вектора обобщенных координат ![]() , формируемых конструктивными и функциональными ограничениями на компоненты вектора
, формируемых конструктивными и функциональными ограничениями на компоненты вектора ![]() .
.
Таким образом, для решения прямой позиционной задачи достаточно вычислить элементы матрицы ![]() и ее произведение на вектор s. Разработанное приложение реализует эти операции. Пример результатов решения прямой позиционной задачи для манипулятора 21 с помощью разработанного приложения приведен на рисунке 2.22.
и ее произведение на вектор s. Разработанное приложение реализует эти операции. Пример результатов решения прямой позиционной задачи для манипулятора 21 с помощью разработанного приложения приведен на рисунке 2.22.

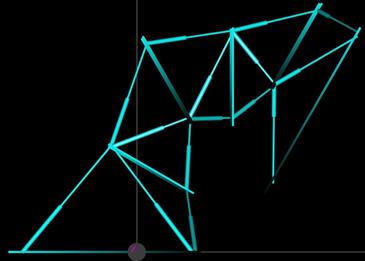
Рисунок 2.22 – К решению прямой позиционной задачи: наклонное положение манипулятора 21 в двух проекциях
2.4.2. Обратная позиционная задача
Для рассматриваемого манипулятора обратная позиционная задача представляет собой задачу определения длин штанг всех секций манипулятора, которые обеспечивают заданное положение и, быть может, ориентацию схвата манипулятора.
В общем виде обратная позиционная задача формулируется следующим образом: при заданном векторе S найти допустимые обобщенные координаты манипулятора ![]() , удовлетворяющие уравнению (2.1)
, удовлетворяющие уравнению (2.1)
Уравнение (2.1) представляет собой систему трех нелинейных тригонометрических уравнений с ![]() неизвестными, где m– размерность каждого из векторов
неизвестными, где m– размерность каждого из векторов ![]() . Эта система уравнений может не иметь ни одного решения (требуемое положение схвата недостижимо), иметь одно решение, иметь бесконечно много решений (требуемое положение схвата может обеспечить бесконечное число конфигураций манипулятора).
. Эта система уравнений может не иметь ни одного решения (требуемое положение схвата недостижимо), иметь одно решение, иметь бесконечно много решений (требуемое положение схвата может обеспечить бесконечное число конфигураций манипулятора).
Для многосекционного манипулятора случай наличия бесконечного множества решений обратной позиционной задачи является типичным. Именно это обстоятельство позволяет ставить задачу поиска в каком-то смысле оптимального решения обратной позиционной задачи.
В рассматриваемом приложении для решения задачи (2.1) применяются итерационный и оптимизационный методы. Важно, что итерационный метод, в отличие от оптимизационного, позволяет получить не только искомое конечное положение манипулятора, но и набор его промежуточных положений, соответствующих переводу манипулятора из начального положения в искомое. С другой стороны, оптимизационный метод, при необходимости, позволяет достаточно легко учитывать дополнительные требования, предъявляемые к искомой конфигурации манипулятора (путем интеграции их в целевую функцию). Далее рассматриваем только итерационный метод.
Суть итерационного метода решения обратной позиционной задачи поясним на простейшем примере двухзвенного манипулятора (рисунок 2.23), где требуемое положение схвата обозначено крестиком [6].
Поворот на малый угол манипулятора вокруг шарнира ![]() приводит к смещению схвата в направлении вектора a, а такой же поворот вокруг шарнира
приводит к смещению схвата в направлении вектора a, а такой же поворот вокруг шарнира ![]() – к смешению схвата в направлении вектора b. Для приведения манипулятора в искомое положение, очевидно, нужно сместить схват
– к смешению схвата в направлении вектора b. Для приведения манипулятора в искомое положение, очевидно, нужно сместить схват ![]() в направлении вектора t. При этом вращение вокруг шарнира
в направлении вектора t. При этом вращение вокруг шарнира ![]() приведет лишь к ухудшению ситуации, а вокруг шарнира
приведет лишь к ухудшению ситуации, а вокруг шарнира ![]() , напротив, поможет уменьшить расстояние от схвата
, напротив, поможет уменьшить расстояние от схвата ![]() до цели.
до цели.
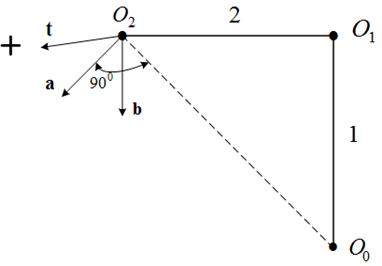
Рисунок 2.23 – Простейший двухзвенный манипулятор
Основная идея итерационного метода решения обратной позиционной задачи состоит в том, что приращения обобщенным координатам в каждом из сочленений манипулятора следует давать на величину, пропорциональную тому, насколько это приращение приближает схват манипулятора к цели. В качестве указанной величины метод использует скалярное произведение: для первого звена – ![]() , для второго звена ‑
, для второго звена ‑ ![]() .
.
2.4.3. Позиционирование манипулятора
При решении задачи позиционирования манипулятора можно использовать два режима. В первом режиме переход в требуемое положение начинается непосредственно из текущего положения, а во втором осуществляется предварительное выведение манипулятора в положение, в котором ось симметрии антенны совпадает с продольной осью симметрии манипулятора. Второй режим позиционирования манипулятора иллюстрирует рисунок 2.24.
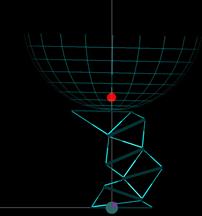





Рисунок 2.24 – Раскадровка второго режима позиционирования схвата манипулятора 21
Разработанное приложение обеспечивает решение задачи позиционирования манипулятора также при условии, что схват манипулятора неподвижен, а направление ![]() требуемым образом ориентировано относительно продольной оси симметрии манипулятора. Эта возможность приложения позволяет решать задачу поворота продольной оси симметрии антенны телескопа на заданный угол при неподвижном схвате (если такой поворот допускает конструкция манипулятора). С точки зрения управления космическим аппаратом эта операция является предпочтительной, поскольку позволяет разгружать двигатели – маховики космического аппарата. Указанную возможность приложения также иллюстрирует рисунок 2.24.
требуемым образом ориентировано относительно продольной оси симметрии манипулятора. Эта возможность приложения позволяет решать задачу поворота продольной оси симметрии антенны телескопа на заданный угол при неподвижном схвате (если такой поворот допускает конструкция манипулятора). С точки зрения управления космическим аппаратом эта операция является предпочтительной, поскольку позволяет разгружать двигатели – маховики космического аппарата. Указанную возможность приложения также иллюстрирует рисунок 2.24.
2.5. Исследование кинематики и динамики многосекционного манипулятора средствами системы MatLabSimulink
2.5.1 Постановка задачи
Рассматриваем пяти секционный манипулятор 21, платформы которого имеют различные размеры, а штанги являются двухсоставными (п.2.2). Расчетная схема секции манипулятора представлена на рисунке 2.25.

![]() - сферические шарниры;
- сферические шарниры; ![]() - шарниры Гука;
- шарниры Гука;
1 ‑ 6 – активные поступательные кинематические пары
Рисунок 2.25 – Расчетная схема гексапода
Принимаем следующие значения параметров гексапода :
- диаметр окружности, на которой лежат точки крепления штанг к основанию нижней секции манипулятора D=2,8026 м;
- диаметр окружности, на которой лежат точки крепления штанг к первым четырем платформам ![]() =1,701 м, к пятой платформе -
=1,701 м, к пятой платформе - ![]() =2,8026 м;
=2,8026 м;
- толщина платформ ![]() =40 мм;
=40 мм;
- массы платформ берутся из расчета, что они изготовлены из трубчатого углепластика прямоугольного сечения с плотностью 1550 кг/м3;
- массы первых четырех платформ равны ![]() =44,3 кг, а масса последней пятой платформы равна
=44,3 кг, а масса последней пятой платформы равна ![]() =60,3 кг;
=60,3 кг;
- нижняя полуштанга каждой из секций имеет внешний диаметр 80 мм, внутренний диаметр – 60 мм;
- верхняя полуштанга каждой из секций имеет внешний диаметр 60 мм, внутренний диаметр – 40 мм;
- масса каждой из штанг ![]() принимается равной 39,3 кг;
принимается равной 39,3 кг;
- полагается, что 2/3 указанной массы штанг сосредоточены в середине штанг (тем самым учитываем массу электропривода штанги).
Рассматриваем два предельных положения манипулятора: а) платформы переведены из транспортного в исходное положение, когда они параллельны друг другу и начинают нормально функционировать двигатели приводов гексаподов – рисуно 2.26; б) манипулятор переведен в одно из рабочих положений, при котором центры масс всех платформ расположены в одной плоскости и плоскость последней пятой платформы перпендикулярна основанию, так что ось симметрии антенны перпендикулярна продольной оси симметрии манипулятора – рисунок 2.27.

Рисунок 2.26 – Первое предельное (исходное) положение
(все платформы параллельны основанию)
В качестве системы автоматического управления (САУ) длинами штанг манипулятора рассматриваем двухконтурную систему с двумя типами регуляторов - пропорциональные регуляторы и ПИД регуляторы. САУ с пропорциональными регуляторами (рисунок 2.28) преобразует разность длин штанг ![]() по формулам
по формулам
![]() ,
,
![]() ,
,
![]() .
.

Рисунок 2.27 – Второе предельное (рабочее) положение
(плоскость последней платформы перпендикулярна основанию)

Рисунок 2.28 – Двухконтурная САУ длиной штанги с пропорциональными регуляторами ![]() ,
, ![]()
САУ с ПИД регуляторами (рисунок 2.29) преобразует разность длин штанг ![]() по формулам
по формулам
 ,
, ![]() ,
,
 .
.

Рисунок 2.29 – Двухконтурная САУ с ПИД регуляторами ![]() ,
, ![]()
2.5.2. Simulink-модель управляемого манипулятора
Используемые в модели системы координат представлены на рисунке 2.30, где углы ![]() определяются формулами
определяются формулами
 ,
,  ,
, ![]() .
.

Рисунок 2.30 – Ориентация системы координат ![]() относительно систему координат
относительно систему координат ![]()
Для удобства работы с моделью в ней выделены следующие подсистемы:
- структурный уровень манипулятора (общая взаимосвязь моделей секций манипулятора);
- уровень секции манипулятора (модель одной секции);
- уровень штанги манипулятора (модель штанги, включая модель ее САУ);
- уровень САУ штангой манипулятора.
Модель манипулятора на верхнем (структурном) уровне иерархии представлена на рисунке 2.31 [7, 8].
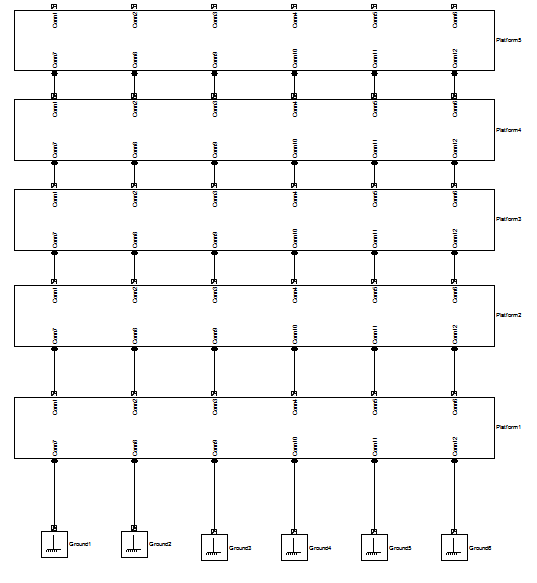
Рисунок 2.31 – Simulink-модель манипулятора на структурном уровне
На рисунке 2.32 представлена модель секции манипулятора, где Body1 – модель платформы, Leg1 - Leg6 – модели штанг, CG – датчик положения центра масс платформы в пространстве. Принято, что платформа является абсолютно жестким телом, у которого имеется масса и моменты инерции.

Рисунок 2.32 – Simulink-модель ступени манипулятора
Simulink-модель штанги манипулятора представлена на рисунке 2.33. Модель включает в себя блоки Body1 – Body4, объединенные блоками линейных перемещений Prismatic. Актуатор моделирует блок Prismatic1, на который подается сигнал о требуемом изменении длины штанги. Блоки Prismatic2, Prismatic3 имитируют упругости штанг. 2/3 массы штанги сосредоточены в блоках Body2, Body1, а 1/3 массы - в блоках Body2 и Body4.
Блоки Body2, Body4 соединены с блоками Gimbal6 и Universal, которые представляют собой модели сферического шарнира и кардана соответственно. К этим блокам подсоединены блоки JointSpring&Damper, имитирующие силы трения в шарнирах.
Также на рисунке 2.33 присутствует связь длины штанги (блок B-A) с блоком RuleSystem1, который есть не что иное, как модель двухконтурной САУ длиной штанги (рисунок 2.34).
Заметим, что представленная модель не включает в себя модели динамики приводов штанг, от которых в значительной степени зависит динамика всего механизма. Поэтому приведенные ниже результаты носят предварительный характер. В случае задания конструкции приводов, представленная модель может быть достаточно просто расширена путем включения в нее их моделей.
2.5.3. Переходные процессы в системе
Выполнено исследование переходных процессов при переводе манипулятора из начального положения в рабочее положение.

Рисунок 2.33 – Simulink-модель штанги с системой управления
Принято, что центры масс всех платформ совершают движение в плоскости ![]() (перемещения по оси 0Zравны нулю).
(перемещения по оси 0Zравны нулю).

Рисунок 2.34 – Модель блока управления с ПИД регуляторами и ограничителями сигнала
Для исследования переходных процессов в момент времени t=4 с подаем ступенчатый сигнал на систему управления каждой из штанга манипулятора. Поскольку рассматриваем плоское движение манипулятора, длины каждой из пар штанг (1¸ 6), (2, 5), (3, 4) изменяем по одному и тому же закону. Начальные и конечные длины штанг всех секций манипулятора приведены в таблице 2.2. Здесь начальные длины штанг соответствуют исходному положению манипулятора, приведенному на рисунке 2.26 (когда начинают нормально функционировать двигатели его приводов. Конечные длины штанг определяют одно из рабочих положений манипулятора (рисунок 2.27).
Таблица 2.2 – Длины штанг манипулятора
Номер секции / положение | Начальное положение
| Конечное положение
|
Секция 1 | 1,15362;1,15362;1,15362;1,15362;1,15362;1,15362 | 1,16787;1,90178;1,90178;1,16787;1,93728;1,93728] |
Секция 2 | 0,81645;0,81645;0,81645;0,81645;0,81645;0,81645 | 1,28914;0,92968;0,92968;1,28914;1,1887;1,1887] |
Секция 3 | 0,81645;0,81645;0,81645;0,81645;0,81645;0,81645 | 0,79628;1,2581;1,2581;0,79628;1,33101;1,33101 |
Секция 4 | 0,81645;0,81645;0,81645;0,81645;0,81645;0,81645 | 1,33335;0,83248;0,83248;1,33335;1,13407;1,13407 |
Секция 5 | 1,15362;1,15362;1,15362;1,15362;1,15362;1,15362 | 1,14958;1,24458;1,24458;1,14958;1,7073;1,7073 |
На рисунках 2.35, 2.36 представлены соответствующие ускорения и координаты центров масс каждой из платформ в функции времени. Результаты соответствуют использованию САУ с пропорциональными регуляторами, когда ![]() =1,5, а
=1,5, а ![]() =5. Значения этих коэффициентов подобраны таким образом, чтобы время переходного процесса составляло примерно 2,5 с.
=5. Значения этих коэффициентов подобраны таким образом, чтобы время переходного процесса составляло примерно 2,5 с.

а) платформа 1

б) платформа 2

в) платформа 2

г) платформа 4

д) платформа 5
Рисунок 2.35 – Ускорения центров масс платформ в функции времени

а) платформа 1
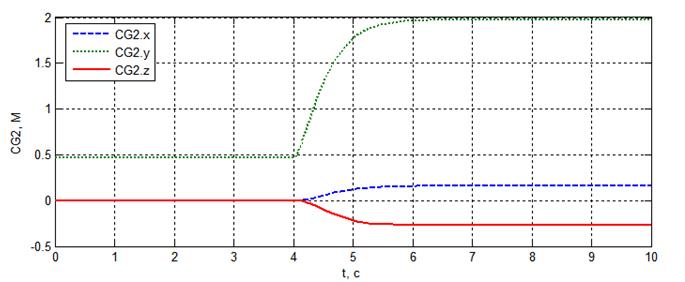
б) платформа 2

в) платформа 3

г) платформа 4
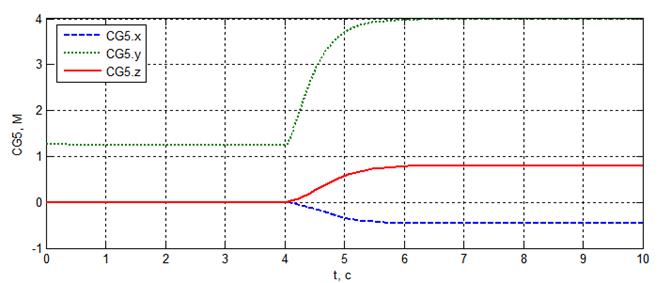
д) платформа 5
Рисунок 2.36 – Координаты центров масс платформ в функции времени
Рисунок 2.35 показывает, что при указанных значениях параметров регуляторов максимальное ускорение развивается пятой платформой и достигает неприемлемой величины, равной примерно 40 ![]() .
.
Рассмотрим теперь САУ длинами штанг манипулятора, параметры регуляторов которой имеют следующие значения: ![]() ;
; ![]() . Данные значения параметров получены нами в предыдущих исследованиях, как оптимальные. Соответствующие усилия в приводах штанг манипулятора представлены на рисунке 2.37. Поскольку перемещения центров масс платформ по оси
. Данные значения параметров получены нами в предыдущих исследованиях, как оптимальные. Соответствующие усилия в приводах штанг манипулятора представлены на рисунке 2.37. Поскольку перемещения центров масс платформ по оси ![]() отсутствует, усилия в приводах каждой из пар штанг (1, 6), (2, 5), (3, 4), очевидно, идентичны.
отсутствует, усилия в приводах каждой из пар штанг (1, 6), (2, 5), (3, 4), очевидно, идентичны.

а) усилия в штангах 1, 6
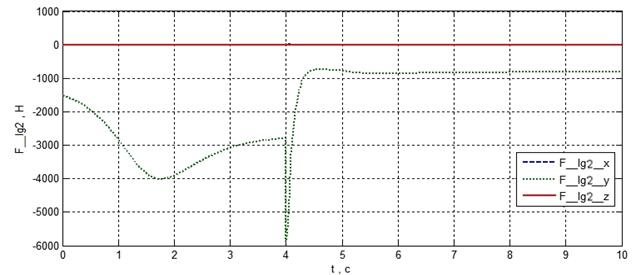
б) усилия в штангах 2, 5

в) усилия в штангах 3, 4
Рисунок 2.37 – Усилий в приводах манипулятора в функции времени
Рисунок 2.37 показывает, что при указанных значениях параметров регуляторов максимальные усилия в приводах штанг достигают примерно 7000 Н.
В целом, разработанная модель позволяет подобрать параметры регулятора, обеспечивающие требуемые характеристики переходного процесса по ускорению и усилиям в приводах.
Еще раз подчеркнем, что представленные результаты являются предварительными, поскольку получены без учета модели динамики приводов штанг.
2.5.4. Амплитудно-частотные и фазо-частотные характеристики САУ длинами штанг манипулятора
Рассматриваем пять регуляторов со следующими значениями параметров:
1) ![]() ;
; ![]() (оба регулятора являются П-регуляторами);
(оба регулятора являются П-регуляторами);
2) ![]() ;
; ![]() (также оба регулятора являются П-регуляторами);
(также оба регулятора являются П-регуляторами);
3) ![]() ;
; ![]() (первый регулятор является ПИ-регулятором , а второй – П-регулятором);
(первый регулятор является ПИ-регулятором , а второй – П-регулятором);
4) ![]() ;
; ![]() (оба регулятора являются ПИ-регуляторами);
(оба регулятора являются ПИ-регуляторами);
5) ![]() ;
; ![]() (также оба регулятора являются ПИ-регуляторами).
(также оба регулятора являются ПИ-регуляторами).
Для каждого из указанных вариантов регуляторов построены амплитудно-частотные и фазо-частотные характеристики, представленные на рисунках 2.38а ‑ 2.38д.

а) ![]() ;
; ![]()
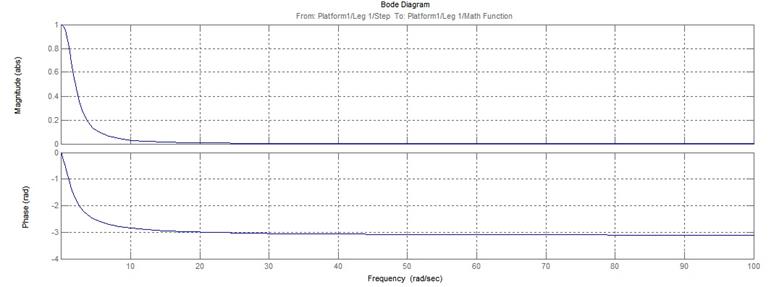
б) ![]() ;
; ![]()

в) ![]() ;
; ![]()

г)![]() ;
; ![]()

д) ![]() ;
; ![]()
Рисунок 2.38 – АЧХ и ФЧХ системы автоматического управления длинами штанг манипулятора
Заключение
В работе решены следующие основные задачи.
а) С помощью разработанного программного приложения, осуществляющее автоматизированное построение 3D Solid Works модели манипулятора, показано, что
‑ пятисекционный манипулятор, имеющий одинаковые платформы и двухсоставные штанги, не позволяет выполнить все необходимые ориентации антенны телескопа;
‑ аналогичный манипулятор с трехсоставными штангами позволяет решить эту задачу;
‑ с помощью пятисекционного манипулятора, имеющего промежуточные платформы меньшего диаметра и двухсоставные штанги, возможно достижение всех необходимых ориентаций антенны телескопа.
Остается открытым вопрос о возможности такого управления последним манипулятором, чтобы во всех случаях центр масс его схвата оставался на продольной оси симметрии манипулятора.
б) Средствами «тяжелой» графической системы NX 7.5 и её приложения «Симуляция кинематических механизмов» построена 3Dгеометрическая модель манипулятора 11, в котором все платформы одинаковы, а штанги являются двухсоставными. С использованием этой модели подтверждена достоверность перечисленных выше результатов. С помощью этой же модели исследована зависимость высоты подъема секции манипулятора от длин ее штанг. Подтверждено, что для перевода манипулятора из транспортного в рабочее положение необходимы дополнительные механизмы.
в) Разработано программное приложение, позволяющее решать прямую и обратную позиционные задачи для многосекционного манипулятора. Приложение поддерживает решение обратной задачи при условии обеспечения неподвижности схвата манипулятора (когда меняется только ориентация оси симметрии антенны). С помощью разработанного приложения показано, что для манипулятора 21 имеется возможность спланировать перемещение оси симметрии антенны, оставляющее неподвижным центр масс системы антенна плюс криоконтейнер. Для синтеза алгоритмов изменения длин штанг, обеспечивающих указанное перемещение, требуются дополнительные исследования.
г) Разработана Simulink-модель пятисекционного манипулятора 21, длины штанг которого управляются с помощью классических ПИД-регуляторов. Выполнено исследование кинематики и динамики переходных процессов в манипуляторе при переводе его из транспортного в рабочее положение. Получены АЧХ и ФЧХ системы управления манипулятором. Разработанная модель позволяет решать задачу выбора оптимальных значений параметров САУ приводами манипулятора. Модель может быть легко модифицирована для исследования эффективности более развитых САУ.
Результаты работы позволяют сделать вывод о принципиальной возможность создания многосекционного манипулятора для наведения космического телескопа «Миллиметрон».
1. Артеменко Ю.Н. Синтез механизмов ориентации космического телескопа «Миллиметрон». 1. Возможности механизмов параллельной структуры для ориентации космического телескопа «Миллиметрон» // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2013. № 1. DOI: 10.7463/0113.0534292
2. Обзор систем CAD/CAM/CAE/GIS. Режим доступа: http://www.cad.dp.ua/obzors/cads.php (дата обращения 20.02.2013).
3. Основные элементы Solidworks 2010. М.: Артания, 2010. 550 с.
4. Гончаров П.С., Ельцов М.Ю., Коршиков С.Б., Лаптев И.В., Осиюк В.А. NX для конструктора-машиностроителя. М.: ИД ДМК Пресс, 2010.504 с.
5. Зенкевич С.Л., Ющенко А.С. Основы управления манипуляционными роботами. М.:МГТУим. Н.Э. Баумана, 2004. 480 с.
6. Hugo Elias. Inverse Kinematics - Improved Methods. Available at: http://freespace.virgin.net/hugo.elias/models/m_ik2.htm , accessed 20.02.2013.
7. Черных И.В. Simulink: Инструмент моделирования динамических систем. Режим доступа: http://matlab.exponenta.ru/simulink/book1/index.php (дата обращения 20.02.2013).
8. Лазарев Ю. Моделирование процессов и систем в MATLAB : учеб. курс. М.: Питер, 2005. 512 c.
Публикации с ключевыми словами: радиотелескоп, космический телескоп «Миллиметрон», механизм параллельной структуры, многосекционный манипулятор
Публикации со словами: радиотелескоп, космический телескоп «Миллиметрон», механизм параллельной структуры, многосекционный манипулятор
Смотри также:
- Синтез механизмов ориентации космического телескопа «Миллиметрон». 3. Синтез механизмов параллельной структуры для ориентации антенны космического телескопа
- Синтез механизмов ориентации космического телескопа «Миллиметрон». 4. Концепция построения интеллектуальной системы активной виброзащиты и высокоточного наведения космического телескопа «Миллиметрон»
- Синтез механизмов ориентации космического телескопа «Миллиметрон». 1. Возможности механизмов параллельной структуры для ориентации космического телескопа «Миллиметрон»
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



