научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#8 август 2004
DOI: 10.7463/0804.0551050
УДК 004.032.26
Россия, Саратовский государственный технический университет
Введение
Информационно-аналитическая система управления снабжением и производством технологической оснастки и инструмента [1, 2] имеет широкие возможности поддержки принятия решения. В частности, система позволяет решать ряд задач анализа и прогнозирования, которые способствуют повышению эффективности управления производством и повышению качества изготавливаемого инструмента.
В общем случае задача прогнозирования заключается в определении значения некоторого параметра (или параметров) системы в будущий момент времени по известным значениям в предыдущие моменты. Примером таких задач является прогнозирование временных рядов, которое эффективно реализуют нейронные сети. В этом случае последующее значение прогнозируемой переменной определяется по нескольким ее предыдущим значениям, а формирование пары обучающих примеров осуществляется по принципу «скользящего окна» [3]. Однако такой упрощенный подход далеко не полностью реализует возможности нейросетей, а в условиях реального производства дает значительные погрешности [4].
Прежде всего следует отметить, что, например, в инструментальном производстве соответствующие временные ряды (загрузка оборудования, потребление энергии, расход материала и т.п.) носят нестационарный характер. Он обусловлен наличием нестационарных производственных факторов и скрытых взаимосвязей, которые влияют на прогнозируемые параметры. Поэтому в подобных случаях необходимо сочетать возможности нейронных сетей по выявлению скрытых закономерностей с прогнозированием временных рядов. Ниже рассмотрены различные подходы к решению задач прогнозирования в инструментальном производстве.
Прогноз загрузки оборудования
При решении задачи прогнозирования на нейронных сетях наиболее важным является вопрос выбора количества и смысла входов и выходов сети. Выбор входных параметров для прогнозирования загрузки оборудования обусловлен типом производственного процесса и стадией производства (заготовительная, стадия обработки и сборочная). Наиболее общий тип процесса – последовательно-параллельный. При этом порядок передачи предметов труда и использования технических ресурсов соответствует многооперационному техпроцессу. Это означает, что каждая деталь или передаточная партия поступает на следующую операцию немедленно, не дожидаясь окончания обработки всей партии деталей на предыдущей операции.
Несмотря на то, что загрузку оборудования можно представить в виде временного ряда, в отличие от известных подходов [3, 4], в данной работе этот прогноз осуществляется не по временным рядам. В качестве входных параметров модели были выбраны следующие данные, которые обусловливают нестационарность процесса:
· тип изделия (норма использования оборудования);
· количество изделий;
· количество незавершенной продукции, которая могла бы пригодиться в обеспечении заказа;
· время поступления заявки на изготовление инструмента;
· степень срочности заказа;
· обеспеченность заказа металлом.
При этом прогнозирование осуществляется для каждой поступившей заявки.
Для прогноза будем использовать нейронную сеть прямого распространения, без обратных связей. В качестве функции активации применим сигмоидальную функцию, а в качестве алгоритма обучения сети – "обратное распространение ошибки". Способ обучения – "с учителем" [3, 4]. Для рассмотрения алгоритма обучения такой сети введем следующие обозначения.
Взвешенные входы:
 ,
,
где wij – веса для соответствующих i–ых входов j-го нейрона, а m– количество нейронов в предшествующем слое, yi -выходы предшествующего слоя.
Выход нейрона:

Суммарная ошибка:
 ,
,
где yj* - желаемое значение j-го выхода.
Рассмотрим алгоритм обратного распространения по шагам.
Шаг 1. Рассчитаем скорость изменения ошибки по каждому выходу последнего слоя: 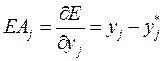 .
.
Шаг 2.Рассчитаем скорость изменения ошибки по взвешенному входу:
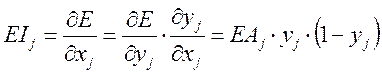
Шаг 3.Рассчитаем ошибку по весу:
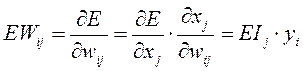
Шаг 4.Далее изменим значение соответствующих весов:
![]()
Шаг 5.Далее повторяем все шаги алгоритма, начиная с первого, для всех слоев сети в их обратном порядке. Для всех слоев, кроме последнего, изменение ошибки по выходу нейрона вычисляется по формуле:

Указанную процедуру следует выполнять для всех обучающих образов до тех пор, пока ошибка не станет достаточно мала.
Данные, поступающие на вход сети, берутся из общей базы за некоторый период времени до момента прогнозирования и входят в состав обучающих входов. Так, при прогнозировании среднемесячной загрузки оборудования в качестве обучающих входных данных берется соответствующая среднемесячная информация за предыдущие 12 месяцев. При прогнозировании на определенную дату берется информация на аналогичную дату в предыдущие 12 месяцев (с необходимой корректировкой последних дней месяца).
На выходе сети имеем загрузку оборудования в часах. Так, при 8-часовой рабочей смене имеем всего три выходных нейрона.
Таким образом, мы тренируем сеть на статистических данных, накопленных в общей базе данных. В результате обучения выявляется скрытая зависимость вида ![]() , где y – выход нейронной сети – прогноз загрузки оборудования, xi – входные данные, обусловливающие загрузку оборудования (тип изделия, его количество и т.д.).
, где y – выход нейронной сети – прогноз загрузки оборудования, xi – входные данные, обусловливающие загрузку оборудования (тип изделия, его количество и т.д.).
Прогноз брака и потребления энергии
В этом случае, так же как и в предыдущем, нейронная сеть определяет скрытые взаимосвязи прогнозируемого параметра от факторов производственного процесса.
Метод прогнозирования брака и потребления энергии выбран один и тот же. Разница только в сущности статистических данных, служащих входной и выходной информацией для нейросетевой модели.
В качестве входов прогнозирования брака используются следующие характеристики:
· срочность заказа;
· номер участка;
· тип оборудования;
· тип изделия;
· количество изделия;
· время поступления заказа.
Вся эта информация берется из общей базы данных, а накапливается она в ходе производственного процесса. В качестве выходов получаем вероятность возникновения брака и прогнозируемое количество брака.
При прогнозировании потребления энергии учитываются справочные данные из таблиц номинальных значений расхода энергии применительно к каждому виду используемого оборудования. В качестве входных данных для прогнозирования затрат энергии используются следующие характеристики:
· номер участка;
· реальная загрузка оборудования в предыдущий период времени;
· прогнозируемая загрузка оборудования.
На выходе модели получаем величину оценочных затрат электроэнергии на выбранном участке.
Так как в данной подзадаче входная информация не представляет собой временной ряд, то имеет смысл применить для прогнозирования нейросетевую модель, использующую кластеризацию входных данных. Из соображений экономии вычислительных ресурсов была выбрана архитектура сети радиальных базисных функций.
Следует также отметить два обстоятельства:
1) входная информация имеет разную размерность,
2) на результат должна влиять близость входных данных не к одному кластеру, а ко всем, но в разной степени.
Исходя из этого, при использовании экстраполяционной модели все входные данные переводятся в соответствующий им код Грея, а при вычислении выходов осуществляется их обратное преобразование в пространство обычных вещественных чисел.
Это промежуточное преобразование повлияет на топологию сети: увеличится число бинарных входов и выходов. Оценка количества нейронов в этих двух слоях производится, исходя из границ реального изменения каждой из входных и выходных величин.
Бинарное кодирование входных и желаемых выходных величин повышает влияние значений входов на выходы (каждый входной разряд индивидуально влияет на каждый разряд выходной величины). Код Грея взят не случайно. Причиной этого является его уникальное свойство: случайное изменение значения одного из разрядов числа в коде Грея повлечет за собой лишь небольшие изменения в значении вещественного числа при декодировании кода. Это предотвращает неадекватное влияние некоторых комбинаций входов на выходы.
Работа с нейросетью производится в соответствии со следующими шагами.
Шаг 1. Выделение кластеров среди входных данных обучающей выборки.
Алгоритм аналогичен обучению сети Кохонена [3], за исключением того, что нейронов во входном слое будет столько, сколько «ядер» входных данных будет обнаружено в результате кластеризации. Надо отметить, что кластеризуемые данные являются бинарными (одной величине будет, как правило, соответствовать несколько входов или выходов, в зависимости от ее разрядности).
Шаг 2. Обучение сети. Выработанные в результате кластеризации «входные ядра» данных присваиваются весовым коэффициентам первого слоя сети, а выходные значения, соответствующие этим ядрам, присваиваются весам нейронов второго слоя сети.
Шаг 3. Перевод входных данных в код Грея.
Шаг 4. Прогнозирование. Выходы первого слоя сети подсчитываются, исходя из значений Евклидова расстояния Yk между входными данными и каждым из ядер (весовых синаптических коэффициентов нейронов первого слоя) ck.:
 ,
,
 ,
,
где i – номер весового синаптического коэффициента, k – номер нейрона (ядра), X – вектор входных бинарных данных, N – количество бит данных во входном векторе, Rad и ![]() – коэффициенты, определяющие форму функции активации нейронов первого слоя, Outk – выход k-го нейрона первого слоя.
– коэффициенты, определяющие форму функции активации нейронов первого слоя, Outk – выход k-го нейрона первого слоя.
Шаг 5. Выходы нейронов второго слоя сети подсчитываются, исходя из суммарного взвешенного сходства входных данных сети со всеми ядрами первого слоя. При этом наибольший приоритет влияния на выходные значения отдается тому выходному нейрону, на соответствующее ядро которого больше «похожа» входная порция данных. Формально это выглядит так:
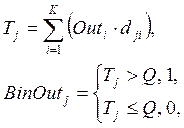
где j – номер выходного нейрона сети, Tj – взвешенное суммарное влияние сходства входных данных со всеми ядрами, K – количество ядер, dji – весовой коэффициент выходного слоя, Q – порог бинаризации суммарного влияния, BinOutj – бинарный выход прогнозируемой величины в коде Грея.
Шаг 6. Перевод значений выходов нейронов второго слоя из кода Грея в обычные вещественные числа, которые и являются реальными выходными значениями прогнозируемой величины.
Прогноз потребности материалов
Наконец, рассмотрим задачу прогнозирования по временным рядам, решение которой учитывает их периодический характер. Входной информацией для решения этой задачи является сводная таблица по использованию материалов за некоторый период времени. От каких параметров может зависеть потребность в материалах на будущий период?
Во-первых, это - номенклатура материала. Действительно, один и тот же материал может использоваться для изготовления различного инструмента. Поэтому для «ходового» материала нужно обеспечить больший запас на складе. Во-вторых, это – периоды времени, в которые данный материал наиболее интенсивно использовался. Эта информация связана с номенклатурой изготавливаемого инструмента, и, следовательно, также определяет потребность в материалах. Заметим, что прогноз потребности материалов может осуществляться для конкретного инструмента, цеха, типа подшипника или в целом.
Из постановки задачи видно, что входная информация (предыстория расхода материалов), связанная со временем, может носить периодический характер. Если представить статистику за прошедший период в виде функции Cm(t), возвращающей значение, предположим, массы материала m, использованного в момент времени t, то требуемую информацию можно извлечь из частотно-временного спектра вектора значений функции Cm за определенный период времени.
Спектр этого типа можно получить с помощью вейвлет преобразования одномерного сигнала Cm(t). Далее, после вычисления спектра, необходимо провести экстраполяцию его значений на период прогноза. Последним этапом будет вычисление результатов обратного вейвлет-преобразования над экстраполированными коэффициентами спектра с помощью вышеописанного персептрона. Это и будет прогноз потребности материала на будущий период, т.е. прогноз, полученный, исходя из частотно-временных свойств функции Cm(t).
Рассмотрим подробнее каждый из этапов.
Этап 1. Сбор статистики по использованию материала за предыдущее время работы.
Подобная информация заносится в общую базу данных штампо-инструментального производства. Происходит пополнение статистики каждый раз, когда работник того или иного склада оформляет расход металла.
Расход оформляется по требованию (по «ярлыку» на металл). Так что сначала в системе следует выбрать требование, еще не обеспеченное металлом или обеспеченное им лишь частично. Система проводит поиск требуемого материала по базе данных и уведомляет пользователя о наличии или отсутствии его.
Если материал есть, то для пользователя подготавливается список складов, с которых можно его израсходовать. Заметим, что одно и то же требование может быть обеспечено с нескольких складов, за несколько операций и не обязательно сразу. После выбора ярлыка пользователь указывает склад, с которого нужно израсходовать металл, и его количество.
В случае успешного завершения этой операции работник склада получает соответствующее уведомление, а технолог, оформивший ярлык, получает сообщение об его полном или частичном обеспечении металлом. В свою очередь, в общую базу данных добавляется запись об истраченном материале (о его марке и количестве) и время операции.
Временная последовательность таких записей по каждому типу материалов порождает нужные нам функции Cm(t).
Этап 2. Расчет частотно-временного спектра функции Cm(t).
Данный этап предполагает использование вейвлет-анализа вектора статистики. Для начала следует выбрать подходящую к задаче скейлинг-функцию ![]() – тот самый сглаживающий фильтр, свертку с которым позже придется вычислять. Далее следует выбрать тип спектральной шкалы, и, если она логарифмическая (это нагляднее), то необходимо выбрать
– тот самый сглаживающий фильтр, свертку с которым позже придется вычислять. Далее следует выбрать тип спектральной шкалы, и, если она логарифмическая (это нагляднее), то необходимо выбрать ![]() – коэффициент увеличения длины скейлинг-функции на каждом шаге анализа. При этом надо обратить внимание на N – длину самого сигнала Cm(t), так как эта величина накладывает ограничения на размеры информативной части самого частотно-временного спектра: чем меньше N, тем меньше должна быть
– коэффициент увеличения длины скейлинг-функции на каждом шаге анализа. При этом надо обратить внимание на N – длину самого сигнала Cm(t), так как эта величина накладывает ограничения на размеры информативной части самого частотно-временного спектра: чем меньше N, тем меньше должна быть ![]() .
.
Далее для каждого масштаба a необходимо произвести свертку сигнала со скейлинг-функцией, длина Pa которой соответствует текущему масштабу a, в соответствии с формулой:
 ,
,
которая при реализации трансформируется в выражение
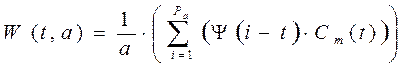 ,
,
где ![]() , P0 – исходная длина скейлинг - функции. Это длина того диапазона значений функции-фильтра
, P0 – исходная длина скейлинг - функции. Это длина того диапазона значений функции-фильтра ![]() , который может оказать необходимое в решаемой задаче воздействие на свертываемый с
, который может оказать необходимое в решаемой задаче воздействие на свертываемый с ![]() сигнал Cm(t). К примеру, для понижения частоты подходит функция MHAT или DOG; для выявления разномасштабных скачков сигнала подойдет сглаженная ступенька и т.д. Однако в данном случае требуется последующее обратное преобразование спектра, и поэтому целесообразно использовать скейлинг-функции из семейства вейвлетов Ингрид Добеши [5].
сигнал Cm(t). К примеру, для понижения частоты подходит функция MHAT или DOG; для выявления разномасштабных скачков сигнала подойдет сглаженная ступенька и т.д. Однако в данном случае требуется последующее обратное преобразование спектра, и поэтому целесообразно использовать скейлинг-функции из семейства вейвлетов Ингрид Добеши [5].
Для каждого необходимого масштаба рассчитывается своя длина Pa фильтра ![]() . Чем выше масштаб, тем эта длина больше, что значительно увеличивает количество арифметических операций на вычисление вектора сверток {W(0, a), W(1, a), W(2, a),…,W(N-1, a)}. Частично пожертвовав точностью и гладкостью получаемого спектра, можно сэкономить на количестве арифметических операций, уменьшая для каждого масштаба a длину N сигнала Cm(t).
. Чем выше масштаб, тем эта длина больше, что значительно увеличивает количество арифметических операций на вычисление вектора сверток {W(0, a), W(1, a), W(2, a),…,W(N-1, a)}. Частично пожертвовав точностью и гладкостью получаемого спектра, можно сэкономить на количестве арифметических операций, уменьшая для каждого масштаба a длину N сигнала Cm(t).
Следует заметить, что c возрастанием величины масштаба aпадает разрешение по времени. То есть, если предположить, что исходный сигнал Cm(t) содержал частотные составляющие в диапазоне от 0 до w, то сигнал – вектор сверток {W(0, a), W(1, a), W(2, a),…,W(N-1, a)} масштаба a - будет содержать все частотные составляющие в диапазоне от 0 до  . Таким образом частотный диапазон сужается, но вместе с этим все менее точно можно отметить координату – время (момент) проявления этих частотных составляющих в сигнале. Применительно к решаемой задаче – это количество металла, расходуемое с данной частотой в вышеупомянутый момент.
. Таким образом частотный диапазон сужается, но вместе с этим все менее точно можно отметить координату – время (момент) проявления этих частотных составляющих в сигнале. Применительно к решаемой задаче – это количество металла, расходуемое с данной частотой в вышеупомянутый момент.
Этап 3. Экстраполяция временного ряда на основе спектра. Данный этап осуществляется с помощью персептрона. При обучении данной сети в качестве входов используются коэффициенты частотно-временного спектра. В качестве выходов – объем требуемого материала в прогнозируемые моменты времени. Для обучения используется накопленная в базе статистика.
Таким образом, в данном случае был учтен периодический характер изменения прогнозируемого параметра – потребности в материале.
Заключение
Нестационарный характер процессов в инструментальном производстве обусловливается наличием скрытых производственных факторов, которые влияют на прогнозируемые параметры. Выявить эти скрытые взаимосвязи весьма эффективно позволяют нейронные сети. Однако методика прогнозирования на нейронных сетях определяется конкретной задачей и, в частности, характером изменения параметров. В рассмотренных задачах получены скрытые функциональные связи параметров и производственных факторов, кластеры, периодическая составляющая временных рядов.
В результате применение нейросетевых алгоритмов прогнозирования в информационно-аналитической системе позволяет более эффективно планировать процесс производства инструмента. Кроме того, особенностью задачи является ее перманентный характер, т.е. через определенное время можно оценить фактическую ошибку прогнозирования. Полученный временной ряд ошибки можно использовать для коррекции модели прогноза.
Литература
1. Булдакова Т.И., Суятинов С.И. Информационно-аналитическая система управления снабжением и производством инструмента // Информационные технологии. – 2002. - № 11. - С. 28-33.
2. Булдакова Т.И., Суятинов С.И. Принципы построения и возможности информационно-аналитической системы управления снабжением и производством инструмента. // Автоматизация и управление в машино- и приборостроении: межвузовский научный сборник. - Саратов: СГТУ, 2002, с. 23-27.
3. Комарцова Л.Г., Максимов А.В. Нейрокомпьютеры. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. – 320 с.
4. Головко В.А. Нейронные сети: обучение, организация и применение. Кн. 4: Учеб. Пособие для вузов /Общая ред. А.И. Галушкина. – М.: ИПРЖР, 2001. – 256 с.
5. Добеши И. Десять лекций по вейвлетам. - Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 464 с.
Публикации с ключевыми словами: прогнозирование, нейронные сети, временные ряды, инструментальное производство, производственные факторы
Публикации со словами: прогнозирование, нейронные сети, временные ряды, инструментальное производство, производственные факторы
Смотри также:
- Модель экстраполяции по максимуму подобия (ЭМП) для временных рядов цен и объемов на рынке на сутки вперед ОРЭМ (Оптовом рынке электроэнергии и мощности)
- Прогнозирование по методам простого и двойного экспоненциального сглаживания
- Прогнозирование по методам тройного экспоненциального сглаживания Хольта Винтерса
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



