научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#11 ноябрь 2004
DOI: 10.7463/1104.0551021
УДК 536.24: 533.6.011
Россия, МГТУ им. Н.Э. Баумана
Введение
В окружающем нас мире регулярно происходит обтекание потоками газа тел различной формы. При этом в потоке газа могут возникать сложные взаимосвязанные процессы, такие как торможение части газа вблизи поверхности тела, теплообмен как внутри потока, так и с омываемым твердым телом и т.д.
Известно, что интенсивность теплообмена между газом и омываемой поверхностью пропорциональна величине температурного напора между ними. При движении газа с небольшой скоростью эта величина равна разности между температурой потока и температурой стенки. В случае же движения газа с большими дозвуковыми и сверхзвуковыми скоростями эта величина равна разности между температурой восстановления (температурой газа на поверхности стенки) и температурой стенки.
Поскольку газ непосредственно у стенки полностью заторможен, то в идеальном случае (при значении критерия Прандтля Pr = 1 и отсутствии теплообмена через стенку) температура газа на поверхности может быть равна температуре торможения. Однако в реальных условиях процесс перехода механической энергии в тепловую сопровождается обменом теплотой и работой между смежными слоями газа. Этот обмен будет иметь место и в том случае, когда стенка теплоизолирована и теплоотдача между ней и газом отсутствует.
При течении реального газа его часть, расположенная вблизи теплоизолированной стенки, будет иметь температуру, в общем случае отличную от температуры торможения. Такую же температуру будет иметь и теплоизолированное тело, находящееся в потоке сжимаемого газа (скачок температуры, как и скачок скорости, может иметь место на границе раздела «твердое тело – газ» только в сильноразреженном газе). Эту температуру называют температурой теплоизолированной стенки или температурой восстановления на стенке (см. [1]) и для газа с постоянной теплоемкостью она определяется одной из формул
где ![]() – коэффициент восстановления температуры,
– коэффициент восстановления температуры, ![]() - скорость потока,
- скорость потока, ![]() - изобарная теплоемкость,
- изобарная теплоемкость, ![]() - статическая (термодинамическая) температура потока газа,
- статическая (термодинамическая) температура потока газа, ![]() - температура торможения газа (полная температура газа), k - показатель адиабаты,
- температура торможения газа (полная температура газа), k - показатель адиабаты, ![]() - число Маха,
- число Маха, ![]() - местная скорость звука,
- местная скорость звука, ![]() - приведенная скорость, акр - критическая скорость.
- приведенная скорость, акр - критическая скорость.
Коэффициент восстановления температуры rпоказывает долю кинетической энергии, которая перешла в теплоту на стенке. Его значение может быть как меньше, так и больше единицы. В работе [2] показано, что при обтекании теплоизолированной пластинки потоком сжимаемого газа возле стенки происходит искривление эпюры температуры торможения (восстановления), причем форма и величина искривления зависят от значения критерия Прандтля
 ,
,
где ![]() - коэффициент кинематической вязкости газа;
- коэффициент кинематической вязкости газа; ![]() - коэффициент теплопроводности газа.
- коэффициент теплопроводности газа.
На рис. 1 показана зависимость безразмерной температуры ![]() от
от ![]() при обтекании теплоизолированной пластины потоком сжимаемого газа (по данным [2]). При этом T* - текущая температура торможения (восстановления) газа, y - координата поперек потока,
при обтекании теплоизолированной пластины потоком сжимаемого газа (по данным [2]). При этом T* - текущая температура торможения (восстановления) газа, y - координата поперек потока, ![]() - толщина пограничного слоя.
- толщина пограничного слоя.
На теплоизолированной стенке выполняются условия ![]() и
и ![]() .
.
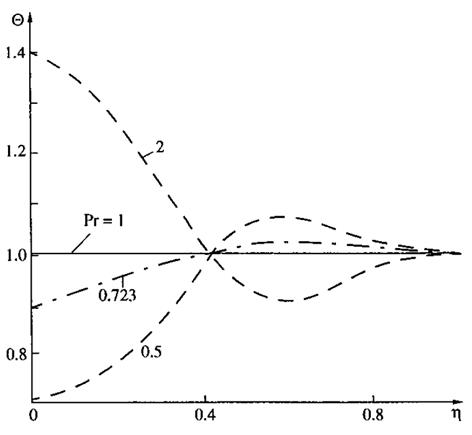
Рисунок 1 - Распределение по сечению пограничного слоя безразмерной температуры торможения при течении сжимаемого газа (по данным [2])
Известно, что момент импульса возле стенки в потоке сжимаемого газа за счет работы сил трения переходит в теплоту, которая отводится за счет механизмов теплопроводности. При равенстве количества теплоты, подводимой за счет работы сил трения, количеству теплоты, которая может быть отведена от стенки механизмами теплопроводности при данной температуре (что соответствует значению критерия Прандтля равного единице) никаких особенностей нет и коэффициент восстановления температуры r = 1. Если интенсивность выделения теплоты за счет работы сил трения преобладает над интенсивностью отвода теплоты в газ механизмами теплопроводности при данной температуре, то Pr > 1 и, соответственно, r > 1. Если преобладает отвод теплоты, тогда Pr < 1 и r < 1.
1 Газодинамическая температурная стратификация
Специфическое распределение эпюры температуры торможения в пограничном слое сжимаемого газа (воздуха) при обтекании тонкой пластины было отмечено в работе Эккерта и Древитца [3] (см. рис. 2). Параметр S можно представить в виде
 ,
,
а относительная поперечная координата определена как
 ,
,
где x, y – координаты вдоль и поперек пластины, ![]() – число Рейнольдса, определенное по параметрам набегающего потока и координате x,
– число Рейнольдса, определенное по параметрам набегающего потока и координате x, ![]() - плотность потока газа.
- плотность потока газа.
На поверхности пластины (при y=0) значение параметра ![]() .
.

Рисунок 2 - Изменение параметра S в пограничном слое сжимаемого газа на тонкой пластине, [3]
На использовании этого эффекта основан способ температурной стратификации в сверхзвуковом потоке газа, предложенный Леонтьевым Александром Ивановичем в 1996 году. Им же было предложено устройство для реализации этого способа (см. рис. 3), получившее название трубы Леонтьева (ТЛ) [4, 5].

1 – ресивер, 2 –дозвуковой канал, 3 – сверхзвуковое сопло, 4 – сверхзвуковой канал, 5 – сверхзвуковой диффузор.
Рисунок 3 - Схема устройства для газодинамической температурной стратификации, [5]
Предельные (максимальные) оценки возможного увеличения температуры торможения потоков в ТЛ рассмотрены в работах [6, 7].
В работе [8] была предложена методика расчета температурной стратификации газа на базе одномерных уравнений газовой динамики. Однако приведенная там методика получена для идеального газа и стенки с нулевой толщиной и термическим сопротивлением. Вопросы влияния формы канала, толщины стенки и ее термического сопротивления рассмотрены в работе [9]. В работах [10, 11] выполнена верификация данной методики, показавшая необходимость ее модернизации. С учетом данных об интенсификации теплообмена на начальном участке (см. работы [1, 12]) и влияния продольного градиента давления и продольной теплопроводности (см. работу [1]) была выполнена модификация расчетной методики и ее верификация по данным, полученным на природном газе [13].
В работах [14-18] было рассмотрено влияние различных факторов на величину газодинамической температурной стратификации и показано, что наибольшее влияние на эффективность работы устройства газодинамической температурной стратификации газа (трубы Леонтьева) оказывает величина коэффициента восстановления температуры r.
В наиболее общем случае коэффициент восстановления температуры зависит от физических свойств потока, режима течения, геометрической формы и особенностей обтекаемой поверхности. При обтекании газом тела заданной формы он является функцией пяти переменных: числа Прандтля, числа Прандтля турбулентного, показателя адиабаты, чисел Рейнольдса и Маха [19].
2 Введение понятия коэффициента восстановления температуры
Первые упоминания о том, что поверхность теплоизолированной стенки имеет температуру, отличную от температуры торможения потока сжимаемого газа, появились после работы Польгаузена [20] в 20-х годах XX века.
Интересные результаты были опубликованы Эккертом и Вайсом [21] в 1940 году, когда они измерили коэффициент восстановления температуры r при поперечном обтекании цилиндра.
В 40-е годы для описания безразмерной температуры в пограничном слое и на поверхности стенки использовался параметр, обычно обозначаемый как S. Спустя 10-15 лет для описания температуры теплоизолированной стенки стал использоваться коэффициент восстановления температуры r, связанный с параметром Sсоотношением
 .
.
По определению коэффициент восстановления температуры показывает долю кинетической энергии, которая перешла в теплоту на стенке.
Данные работы [21] об изменении параметра S(и пересчет на r) по поверхности цилиндра (в зависимости от угла по обводу цилиндра) представлены на рисунке 4.
Из данных, представленных на рис. 4, видно, что по мере приближения к задней лобовой точке наблюдалось существенное уменьшение коэффициента восстановления температуры вплоть до отрицательных значений. Это значит, что температура поверхности цилиндра на подветренной стороне может быть ниже термодинамической температуры набегающего потока.
В дальнейшем в работе Киросака [22] было отмечено существенное влияние на стратификацию энергии генерируемых акустических волн, особенно в области резонанса с отрывом вихрей от поверхности цилиндра.

Рисунок 4 - Значение параметра S и коэффициента восстановления температуры r на поверхности цилиндра, обтекаемого потоком сжимаемого газа, [21]
3 Исследование значения коэффициента восстановления температуры на непроницаемой поверхности
Опыты показывают, что значения коэффициента восстановления температуры при турбулентном обтекании конуса с нулевым углом атаки почти не отличаются от его значений, полученных при продольном обтекании пластины [19]. При ламинарном пограничном слое его значения на пластине больше, чем на конусе и других телах с криволинейной поверхностью.
В работе [23] показано, что для чисел Прандтля 0,6 – 2,0 для ламинарного пограничного слоя коэффициент восстановления температуры хорошо описывается выражением
![]() . (2)
. (2)
Там же приведены данные по значениям коэффициента восстановления при обтекании цилиндрических зондов (проволоки). Пример экспериментальных данных работы [23] представлен на рис. 5.

Рисунок 5 - Влияние скорости потока, расстояния до среза сопла и диаметра цилиндрических зондов на значение коэффициента восстановления температуры, [23]
Из аппроксимации точного решения уравнений Блазиуса для ламинарного пограничного слоя сжимаемого газа (согласно данных работы [24]) на плоской пластине для чисел Прандтля 0,72 – 1,2, чисел Маха от 0 до 10 и показателя степени n в зависимости вязкости и теплопроводности от температуры [1] в пределах 0,5 – 1,25, коэффициент восстановления температуры хорошо описывается выражением (2).
Аналитические исследования для дозвукового потока были подтверждены экспериментально Хилтоном [25] (измерение адиабатной температуры поверхности тонкой пластины), и Эккертом и Вейсом [26] (для случаев обтекания плоской пластины и осесимметричного течения вдоль цилиндрического зонда).
Для турбулентного пограничного слоя для чисел Прандтля от 0,5 до 2 и при постоянных свойствах потока Акерман [27] определил величину коэффициента восстановления температуры, которая может быть определена выражением:
![]() (3)
(3)
В развитом турбулентном потоке зависимость коэффициента r от физических свойств газа и числа Рейнольдса выражается теоретическими формулами Г. Джонсона и М.В. Рубезина [27]
![]()
и Себана [28]

где Re – число Рейнольдса, составленное по параметрам внешнего потока и по расстоянию от начала обтекаемой поверхности.
Влияние числа Маха на величину коэффициента r учитывается теоретической формулой Туккера и Мазлена [19].
![]() ,
,
где  ,
, ![]() .
.
Анализ, выполненный в работе [19] показал, что многие исследователи предлагают для определения коэффициента восстановления температуры использовать число Прандтля турбулентное ![]() , где
, где ![]() - турбулентный коэффициент кинематической вязкости газа;
- турбулентный коэффициент кинематической вязкости газа; ![]() - турбулентный коэффициент теплопроводности газа.
- турбулентный коэффициент теплопроводности газа.
Но если значения простого (так называемого ламинарного) Pr можно взять из таблиц физических свойств газов, то оценить величину PrT сложнее, поскольку нет опытных данных для надежного определения турбулентных коэффициентов вязкости и теплопроводности.
Удобнее определять величину PrT по измеренным значениям температуры восстановления, а, следовательно, и коэффициента восстановления температуры. Эти измерения выполнить легче, чем измерения PrT. Однако нужно иметь в виду, что большинство этих выражений относится по существу к течению газа с не очень высокими скоростями, тогда как коэффициенты восстановления температуры измерялись только при течении сжимаемого газа на теплоизолированной поверхности.
Кроме того, эти зависимости достаточно сложные и имеют ряд ограничений. Характерным их представителем является аналитическое выражение для коэффициента восстановления температуры в турбулентном потоке идеального газа, полученное в работе [29]
 , (4)
, (4)
где ![]() - универсальная постоянная, характеризующая пути перемешивания.
- универсальная постоянная, характеризующая пути перемешивания.
Во многих расчетах принимают (следуя аналогии Рейнольдса) PrT = 1 (см., например, [30]). Однако экспериментальные работы по определению PrT на основе измеренных профилей скорости и температуры в каналах указывает на отклонение PrT от единицы и на зависимость его от чисел Рейнольдса и Прандтля. Но эту связь нельзя считать однозначной.
Некоторому упорядочиванию неоднозначных экспериментальных данных способствует теоретический подход, предложенный в работе [31]. Согласно этой работе в области Pr<1 турбулентное число Прандтля по мере снижения числа Прандтля ламинарного возрастает и принимает значение больше единицы. В области Pr≈1 значение PrT ≈1 и в области Pr>>1 значение PrT ≈0,66. Этот вывод подтверждается экспериментальными данными по теплообмену работы [32].
В соответствии с данными работ [28, 30] с ростом числа Рейнольдса турбулентное число Прандтля уменьшается для газов с Pr<1 и увеличивается для газов с Pr>1. При больших числах Рейнольдса это влияние исчезает и PrT ≈→0,9.
Использование предположения о постоянном значении PrT по всей области ядра потока дает весьма хорошие результаты при расчетах теплоотдачи. Но, в то же время, сложным является вопрос о поведении PrT вблизи стенки - в области пограничного слоя. Наиболее часто принимают условие PrT = const. Хотя такой подход приводит к хорошему согласию с экспериментальными данными по теплопередаче, однако не является строгим.
Большое количество исследований дают значение PrT =1,2 – 2, что привело бы к значению r = 1,1 – 1,3. При этом обработка имеющихся экспериментальных данных по турбулентному обтеканию теплоизолированных тел потоком сжимаемого воздуха дает r = 0,87 ‑ 0,9. На основании этого можно сделать вывод о том, что определение коэффициента восстановления температуры через PrTне совсем корректно.
Гухман А.А., Илюхин Н.В. и др. изучали зависимость коэффициента восстановления от чисел Re и М для продольно обтекаемой термопары [32]. Установлено, что в широком диапазоне параметров коэффициент r постоянен и равен 0,90. Одновременно есть данные о том, что коэффициент восстановления температуры не зависит от числа Маха [18], и данные о том, что при обтекании воздушным потоком конуса в пределах чисел M =1,33 – 4,5 он немного увеличивается с ростом числа Маха и в среднем r = 0,88 ± 0,01 [19].
При этом в обоих случаях величина коэффициента восстановления температуры находится в хорошем соответствии с определением по формуле ![]() (в условиях проведенных опытов имело место
(в условиях проведенных опытов имело место ![]() ).
).
И.P. Сталдер, М.В. Рубезин и Т. Тенделанд [33] выполнили анализ влияния режима течения и числа Маха на значение коэффициента восстановления температуры (см. рис. 6) и исследовали коэффициент восстановления в турбулентном потоке на пластине при М=2,4.
Полученные ими экспериментальные данные о зависимости коэффициента восстановления температуры для пластины от числа Рейнольдса приведены на рисунке 7. Число Рейнольдса отнесено к условиям на границе пограничного слоя и к расстоянию от передней кромки.

Рисунок 6 - Таблица из работы [33], посвященная анализу влияния режима течения, типа модели и числа Маха на значение коэффициента восстановления температуры

Рисунок 7 - Изменение коэффициента восстановления температуры в зависимости от числа Рейнольдса при обтекании пластины, [33]
В работе [34] представлены экспериментальные данные, показывающие, что для чисел Маха M =0,37 – 1 при течении воздуха по трубке коэффициент восстановления температуры меняется от 0,82 до 0,89.
В работах [35, 36] авторы не выявили значительного изменения r от числа Маха при ламинарном и развитом турбулентном пограничном слое. Зависимость коэффициента восстановления температуры от числа Рейнольдса для 10° конуса при числе Маха равном 3,5 по данным работы [35] приведена на рис. 8.
Зависимость коэффициента восстановления от числа Рейнольдса для комбинированного тела, состоящего из 12º конуса и цилиндра, при числе Маха равном 3,5 по данным работы [36] приведена на рис. 9. Приведенные на рис. 8 и 9 данные относятся к случаю обтекания конических тел потоком воздуха при нулевом угле атаки. Число Рейнольдса посчитано по параметрам невозмущенного потока, расстояние отсчитывалось от кромки тела по образующей.

Ref. 5 – расчет, выполненный по данным работы [37].
Рисунок 8 – Внешний вид модели и изменение коэффициента восстановления температуры по длине конического тела при разных числах Рейнольдса, [35]
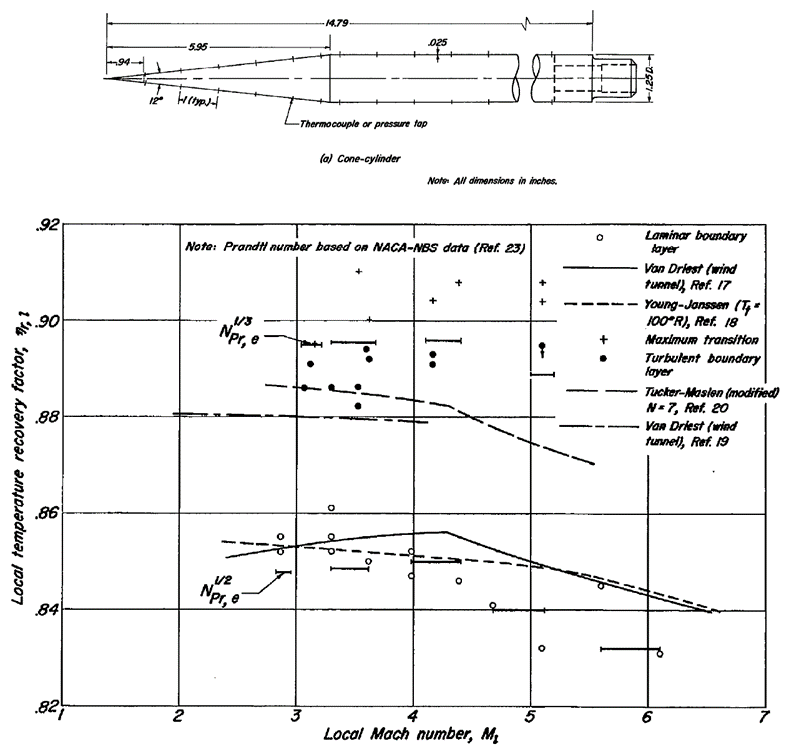
Ref. 17 – расчет, выполненный по данным работы [38], Ref. 18 – расчет по [39], Ref. 19 – расчет по [40], Ref. 20 – расчет по [37].
Рисунок 9 - Изменение локального значения коэффициента восстановления температуры в зависимости от числа Маха по данным [36]
Зависимость коэффициента восстановления температуры при обтекании теплоизолированных тел потоком воздуха в зависимости от числа Рейнольдса при T = 55,6°Cи Pr = 0,71 по данным работы [19] показана на рисунке 10.

1 ‑ по формуле (4); 2 ‑ ![]() ; 3 ‑ данные лаборатории баллистических исследований (США), обтекание воздухом конуса 10° при M = 2,2; 4 ‑ данные Массачусетского технологического института (США), обтекание воздухом пластины при М = 3,0; 5 – данные Национального консультативного Совета по аэронавтике (США), обтекание воздухом конуса 10° при М = 3,8
; 3 ‑ данные лаборатории баллистических исследований (США), обтекание воздухом конуса 10° при M = 2,2; 4 ‑ данные Массачусетского технологического института (США), обтекание воздухом пластины при М = 3,0; 5 – данные Национального консультативного Совета по аэронавтике (США), обтекание воздухом конуса 10° при М = 3,8
Рисунок 10 – Зависимость значения коэффициента восстановления температуры в турбулентном пограничном слое от числа Рейнольдса, [19]
Большинство опытных данных показывает, что при продольном турбулентном обтекании простых тел (пластина, конус, цилиндр) значение коэффициента восстановления почти не зависит от чисел Рейнольдса и Маха [1, 28, 41, 42]. Аналогичная картина наблюдается и при ламинарном течении газа [1, 43].
Для тел со сложной формой поверхности коэффициент восстановления температуры определить сложнее, т.к в общем случае он зависит от физических свойств потока, режима течения, геометрической формы и особенностей обтекаемой поверхности, числа Прандтля ![]() и числа Прандтля турбулентного
и числа Прандтля турбулентного ![]() .
.
Практически все приведенные экспериментальные данные, полученные для воздуха при отсутствии продольного градиента давления в широком диапазоне чисел Маха и Рейнольдса, для пластины продольно обтекаемой турбулентном потоком газа хорошо описываются зависимостью ![]() (в диапазоне чисел Прандтля от 0,5 до 2). Для тел со сложной формой поверхности коэффициент восстановления температуры определить сложнее [18, 19].
(в диапазоне чисел Прандтля от 0,5 до 2). Для тел со сложной формой поверхности коэффициент восстановления температуры определить сложнее [18, 19].
Таким образом, остается вопрос определения значения числа Прандтля. Для большинства чистых газов и воздуха (по данным работ [44-46]) значение числа Прандтля составляет от 0,7 до 1,0. Однако малоизвестным фактом является то, что для смесей легких и тяжелых газов значение числа Прандтля может быть значительно ниже.
4 Влияние параметров вдува на величину коэффициента восстановления температуры
Вопросу исследования влияния параметров вдува на значение коэффициента восстановления температуры было посвящено много работ (см., например, [1, 47-52]). Например, в работе [1] представлены результаты экспериментального исследования и приведена формула, описывающая изменение коэффициента восстановления температуры в достаточно широком диапазоне значений параметра вдува
 , (5)
, (5)
где  – параметр вдува,
– параметр вдува, – число Стентона, определенное при тех же параметрах основного потока, но при отсутствии вдува (jСТ = 0), jСТ - массовый расход вещества, выдуваемого из пористой стенки.
– число Стентона, определенное при тех же параметрах основного потока, но при отсутствии вдува (jСТ = 0), jСТ - массовый расход вещества, выдуваемого из пористой стенки.
Сравнение результатов расчета по формуле (5) с экспериментальными данными [1] и другими известными результатами [49, 53, 54] представлено на рисунке 11.

экспериментальные данные для воздуха при разных числах Маха: 1 – М = 3,2; 2 – М = 2,5; 3 – М = 2,05, 3,05, 4; 4 – М = 4,7 [53]; 5 – М = 3 [49]; 6 – М = 2,7 [54]; 7 - расчет по (5)
Рисунок 11 - Влияние параметра вдува на величину коэффициента восстановления от температуры по данным работы [1]
Проведенный анализ подтвердил применимость этой зависимости до значений параметра вдува bm = 6 и чисел Маха 3 ‑ 3,5.
В работе [48] представлены данные о влиянии завесы, возникающей за пористым участком со вдувом, на величину коэффициента восстановления температуры. Графики, демонстрирующие влияние параметра вдува на величину коэффициента восстановления температуры в области завесы и за ней, представлены на рисунке 12, построенном по данным работы [48]

1 ‑ bm = 2,6; 2 ‑ bm = 4,0; 3 ‑ bm = 4,5; 4 ‑ bm = 5,1; 5 ‑ bm = 5,2.
Рисунок 12 – Влияние параметра вдува на величину коэффициента восстановления температуры в области газовой завесы и за ней; по данным [48]
Из данных, представленных на рис. 11 и 12, видно, что даже при значении числа Прандтля Pr = 0,7 значение коэффициента восстановления температуры при турбулентном течении воздуха за счет вдува может снизиться до уровня 0,5 против ![]() .
.
Заключение
Проведенный анализ показал, что при продольном ламинарном обтекании пластины или цилиндрического (конического) тела потоком воздуха в широком диапазоне чисел Маха и Рейнольдса значение коэффициента восстановления температуры r = 0,85 ± 0,012, т.е. для его определения можно использовать формулу ![]() . Эта формула для диапазона значений чисел Прандтля Pr = 0,69 – 0,72 дает значение коэффициента восстановления температуры в диапазоне r = 0,83 – 0,85.
. Эта формула для диапазона значений чисел Прандтля Pr = 0,69 – 0,72 дает значение коэффициента восстановления температуры в диапазоне r = 0,83 – 0,85.
Показано, что при ламинарном течении газа продольный градиент давления практически не влияет на величину коэффициента восстановления температуры, для определения которого в диапазоне чисел Прандтля от 0,6 до 2 можно использовать формулу ![]() .
.
Проанализировано влияние различных параметров и показано, что при продольном турбулентном обтекании простых тел (пластина, конус, цилиндр) значение коэффициента восстановления почти не зависит от чисел Рейнольдса и Маха и в диапазоне чисел Прандтля от 0,5 до 2 может быть определено по формуле ![]() . Показано, что продольный градиент давления приводит к снижению величины r.
. Показано, что продольный градиент давления приводит к снижению величины r.
При ламинарном и турбулентном обтекании тел со сложной формой поверхности коэффициент восстановления определить сложнее. В общем случае он оказывается ниже, чем при продольном обтекании тел простой формы.
Показано, что возможно сильное снижение коэффициента восстановления температуры даже при вдуве однородного газа. В этом случае использование формул ![]() для ламинарного и
для ламинарного и ![]() и турбулентного режима оказывается не корректным даже для случая вдува воздуха в воздух.
и турбулентного режима оказывается не корректным даже для случая вдува воздуха в воздух.
Список литературы
1. Кутателадзе С.С., Леонтьев А.И. Тепломассообмен и трение в турбулентном пограничном слое. 2-е изд., перераб. М.: Энергоатомиздат. 1985. 320 с.
2. Леонтьев А.И. Газодинамические методы температурной стратификации (обзор) // Известия РАН. Механика жидкости и газа. 2002. № 4. С. 6-26.
3. Eckert E., Drewitz O. Die Berechnung des Temperaturfeldes in der laminaren Grenzschicht schnell angeströmter, unbeheizter Körper (in German) // Luftfahrt-Forschung. 1942. Bd. 19. S. 189-196.
4. Леонтьев А.И. Способ температурной стратификации газа и устройство для его осуществления (Труба Леонтьева) : пат. 2106581 РФ. Заявл 23.05.1996; опубл. 10.03.1998, Бюл. № 7.
5. Леонтьев А.И. Газодинамический метод энергоразделения газовых потоков // Теплофизика высоких температур. 1997. Т. 35, № 1. С. 157-159.
6. Леонтьев А.И. Температурная стратификация сверхзвукового газового потока // Доклады Академии Наук. 1997. Т. 354, № 4. С. 475-477.
7. Леонтьев А.И. Температурная стратификация в сверхзвуковом потоке // Литовская АН. Энергетика. 1998.№ 2. С. 35-42.
8. Бурцев С.А. Исследование температурной стратификации газа // Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 1998. № 2. С. 65-72.
9. Бурцев С.А. Оптимизация геометрии сверхзвукового канала в устройстве для энергоразделения // Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 1999. № 2. С. 48-54.
10. Бурцев С.А. Исследование температурного разделения в потоках сжимаемого газа : дис. ... канд. техн. наук. М., 2001. 124 с.
11. Леонтьев А.И., Бурцев С.А., Визель Я.М., Чижиков Ю.В. Экспериментальное исследование газодинамической температурной стратификации природного газа // Газовая промышленность. 2002. № 11. С. 72-75.
12. Леонтьев А.И., Миронов Б.П., Фафурин А.В. Длина начального участка при турбулентном течении газа в цилиндрической трубе в условиях существенной неизотермичности // Журнал прикладной механики и технической физики. 1968. № 4. С. 99-104.
13. Бурцев С. А. Исследование устройства температурной стратификации при работе на природном газе // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2004. № 9. DOI: 10.7463/0904.0516097
14. Виноградов Ю.А., Ермолаев И.К., Леонтьев А.И. Течение газа в сверхзвуковом осесимметричном сопле с проницаемой вставкой // Известия РАН. Механика жидкости и газа. 1999. № 5. С. 205-208.
15. Макаров М.С. Влияние реальных свойств газа на коэффициент восстановления и коэффициент трения в сверхзвуковом пограничном слое // Труды 3 Российской национальной конференции по теплообмену. М.: Издательство МЭИ, 2002. Т. 8. C. 32-35.
16. Бурцев С.А., Леонтьев А.И. Температурная стратификация в сверхзвуковом потоке газа // Известия РАН. Энергетика. 2000. № 5. С. 101-113.
17. Leontiev A.I. New Methods of Gas-Dynamic Temperature Stratification // In: Low Temperature and Cryogenic Refrigeration / S. Kakac, et all, eds. Kluwer Academic Publishers, 2003. P. 249-263.
18. Энерготехнологии / В.П. Александренков, Т.В. Баженова, С.А. Бурцев и др. // Научные основы технологий XXI века / Под ред. А.И. Леонтьева, Н.Н. Пилюгина, Ю.В. Полежаева, В.М. Поляева. М.: УНПЦ Энергомаш, 2000. С. 58-96.
19. Романенко П.Н. Тепломассообмен и трение при градиентном течении жидкостей. М.: Энергия, 1971. 568 с.
20. Pohlhausen E. Der Wärmeaustausch zwischen festen Körpern und Flüssigkeiten mit kleiner reibung und kleiner Wärmeleitung (in German) // Zeitschrift für Angewandte Mathematik und Mechanik. 1921. Vol. 1, iss. 2. P. 115-121. DOI: 10.1002/zamm.19210010205
21. Eckert E., Weise W. Messung der Temperaturverteilung auf der Oberflache Schnell Angestromter Unbeheizter Korper // Forschg. Ing. Wessen. 1940. Bd. 13. S. 213-234.
22. Kurosaka M. Acoustic Strieaming in Swirling Flow and the Ranque-Hilsch Effect // J. Fluid Mech. 1982. Vol. 124. P. 139-172. DOI: http://dx.doi.org/10.1017/S0022112082002444
23. Eckert E., Weise W. Die Temperatur unbeheizter Körper in einem Gasstrom hoher Geschwindigkeit // Forschung auf dem Gebiete des Ingenieurwesens. Jan-Feb. 1941. Vol. 12, no 1, pp. 40-50.
24. Johnson H., Rubesin M.W. Aerodynamic heating and convective heat transfer-summary of literature survey // Trans. ASME. 1949. Vol. 75, no. 5. P. 447-452.
25. Hilton W.F. Thermal effects on bodies in an air streams // Proceedings of the Royal Society of London. Series A. October 1938. Vol. 168. P. 43-57.
26. Eckert E., Weise W. Measurement of temperature distribution on the surface of unheated bodies in hight velocity flow // Forschung auf dem Gebiete des Ingenieurwesens. 1942. Vol. 13. P. 246-254.
27. Ackerman G. Plate thermometre in hight velocity flow with turbulent boundary layer // Forschung auf dem Gebiete des Ingenieurwesens. 1942. Vol. 13. P. 226-235.
28. Турбулентные течения и теплопередача : сб. статей / под ред. Линь-Цзя-Цзяо; пер. с англ. В.П. Шидловского. М.: Изд‑воиностраннойлитературы, 1963. 564 с.
29. Seban R.A. Analysis for the heat transfer to turbulent boundary layers in high velocity flow: Ph.D. Thesis. Berkeley, Univ. of Calif., 1948. 234 p.
30. Ибрагимов М.Х., Субботин В.И., Бобков В.П., Сабелев Г.И., Таранов Г.С. Структура турбулентного потока и механизм теплообмена в каналах. М.: Атомиздат, 1978. 296 с.
31. Tyldessley J.R., Silver R.S. The production of the transport properties of a turbulent fluid // Intern. J. Heat Mass Transfer. 1968. Vol. 11, no. 9. P.1325-1347.
32. Гухман А.А., Кадер Б.А. Массоотдача от стенки трубы к турбулентному потоку жидкости при больших числах Шмидта // Теоретические основы химической технологии. 1969. Т. 3, № 2. С. 216-243.
33. Stalder J.R., Rubezin M.W., Tendeland T. A determination of the laminar-transitional and turbulent boundary layer temperature recovery factors on a flat plate in supersonic flow : NACA-TN-2077. 1950. 21 p
34. McAdams W.H., Nicolai L.A., Keenan J.H. Measurements of recovery factors and coefficients of heat transfer in a tube for subsonic flow of air : NACA-TN-985. 1945. 30 p.
35. Jack J.R., Moskowitz B. Experimental investigation of temperature recovery factors on a 10 degree cone at angle of attack at a Mach number of 3.12 : NACA-TN-3256. 1954. 16 p.
36. Reller J.O H., Frank M. Temperature recovery factors on a slender 12 degree cone-cylinder at Mach numbers from 3.0 to 6.3 and angles of attack up to 45 degrees : NACA-RM-A55G20. 1955. 59 p.
37. Tucker M., Maslen S.H. Turbulent boundary-layer temperature recovery factors in two-dimensional supersonic flow : NACA-TN-2296. 1951. 21 p.
38. Van Driest E.R. The laminar boundary layer with variable fluid properties // Preprints of Papers, Heat Transfer and Fluid Mechanics Institute. 1954. Vol. 7. P. 127-141.
39. Young G.B.W., Janssen E. The compressible boundary layer // Jour. Aero. Sci. Apr. 1952. Vol. 19, no. 4. P. 229-236; 288.
40. Van Driest E.R. The turbulent boundary layer with variable Prandtl number : Rep. No. AL-1914. North American Aviation, Inc., Apr. 2, 1954. 68 p.
41. Mack L.M. An experimental investigation of the temperature recovery factor : NACA Report JPL-20-80. 1954. 23 p.
42. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. М.-Л.: Энергия, 1965. 424 с.
43. Петухов Б.С. Теплообмен в движущейся однофазной среде. Ламинарный пограничный слой: Монография. М.: Изд-во МЭИ, 1993. 352 с.
44. Таблицы физических величин : Справочник / под ред. И.К. Кикоина. М.: Атомиздат, 1976. 1008 с.
45. Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. М.: Наука, 1972. 720 с.
46. Физические величины: Справочник / под ред. И.С. Григорьева, Е.З. Мейлихова. М.: Энергоатомиздат, 1991. 1232 с.
47. Goldstein R.G., Eckert E.R.G., Wilson D.J. Film cooling with normal injection into a supersonic flow // Trans. ASME. Ser. B. 1968. Vol. 90, № 4. P. 584-589.
48. Коэффициенты восстановления на проницаемой поверхности и в области газовой завесы в сверхзвуковом турбулентном пограничном слое / Ю.В. Барышев, Ю.А. Виноградов, А.И. Леонтьев, В.И. Рождественский // Известия АН СССР. Механика жидкости и газа. 1972. № 2. С. 131-136.
49. Харченко В.Н. Теплообмен в сверхзвуковом турбулентном пограничном слое при вдуве охлаждающего газа через щель // Теплофизика высоких температур. 1972. Т. 10, № 1. С. 101-105.
50. Кутателадзе С.С., Леонтьев А.И. Тепломассообмен и трение в турбулентном пограничном слое. М.: Энергия. 1972. 340 с.
51. Барышев Ю.В., Леонтьев А.И., Пейкер Н.К. Турбулентный пограничный слой на проницаемой поверхности при интенсивных вдувах // Инженерно-физический журнал. 1976. Т. 30, № 5. С. 773-779.
52. Волчков Э.П. Пристенные газовые завесы. Новосибирск: Наука, 1983. 240 с.
53. Bartle E., Leadon B. Experimental evaluation of heat transfer with transpiration cooling in a turbulent boundary layer at M=3.2 // Journ. Aero. Sci. 1960, vol. 27, no. 1. P. 334-337.
54. Rubesin M.W. An analytical estimation of the effect of transpiration cooling on the heat-transfer and skin-friction characteristics of a compressible, turbulent boundary layer : NACA-TN-3341. 1954. 57 p.
Публикации с ключевыми словами: число Прандтля, коэффициент восстановления температуры, ламинарный пограничный слой, турбулентный пограничный слой, сверхзвуковой поток, энергоразделение, метод газодинамической температурной стратификации
Публикации со словами: число Прандтля, коэффициент восстановления температуры, ламинарный пограничный слой, турбулентный пограничный слой, сверхзвуковой поток, энергоразделение, метод газодинамической температурной стратификации
Смотри также:
- Численное моделирование влияния числа Прандтля газа и схемы течения на эффективность работы устройства безмашинного энергоразделения
- Экспериментальное исследование коэффициента восстановления температуры и интенсификации теплоотдачи при течении на плоской стенке за ребром сверхзвукового потока сжимаемого газа
- Исследование влияния состава бинарных смесей инертных газов на их теплофизические свойства
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||

 или
или  (1)
(1)


