научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2013
DOI: 10.7463/0313.0550970
УДК 621.3 + 681.3
Россия, Новосибирск, Институт вычислительной математики и математической геофизики СО РАН.
Введениеи постановка задачи.
В работе рассматривается проблема синтеза алгоритма (модели) ![]() как задача поиска параметров и функций данного темплейта (шаблона, скелетона)
как задача поиска параметров и функций данного темплейта (шаблона, скелетона) ![]() алгоритма с целью оптимизации заданной функции
алгоритма с целью оптимизации заданной функции ![]() , характеризующей качество алгоритма. Темплейт (шаблон, скелетон)[1-3] представляет собой управляющую параметризованную структуру алгоритма, которая описывает порядок сканирования структур данных алгоритма и определяет динамику вычислительного процесса в пространственно-временных координатах.
, характеризующей качество алгоритма. Темплейт (шаблон, скелетон)[1-3] представляет собой управляющую параметризованную структуру алгоритма, которая описывает порядок сканирования структур данных алгоритма и определяет динамику вычислительного процесса в пространственно-временных координатах.
Пусть темплейт ![]() алгоритма
алгоритма ![]() содержит (неопределенные) параметры
содержит (неопределенные) параметры ![]() описывающие значения целочисленных и действительных коэффициентов и переменных, значения индексов, величины инкрементов и декрементов, а также представляющие знаки переменных, логические операции и отношения, типы округления переменных. Пусть темплейт
описывающие значения целочисленных и действительных коэффициентов и переменных, значения индексов, величины инкрементов и декрементов, а также представляющие знаки переменных, логические операции и отношения, типы округления переменных. Пусть темплейт ![]() содержит множество (неизвестных) предикатов и функций (формул) алгоритма
содержит множество (неизвестных) предикатов и функций (формул) алгоритма ![]() . При задании значений параметров
. При задании значений параметров ![]() и определении предикатов и функций (формул)
и определении предикатов и функций (формул) ![]() в данном темплейте
в данном темплейте ![]() мы получаем (синтезируем) алгоритм
мы получаем (синтезируем) алгоритм ![]() . Если задан набор значений входных параметров алгоритма
. Если задан набор значений входных параметров алгоритма ![]() -
- ![]() ,
, ![]() , и задан набор значений выходных параметров
, и задан набор значений выходных параметров ![]() ,
, ![]() , которые необходимо получить в результате исполнения алгоритма, то качество работы алгоритма будет характеризовать функция
, которые необходимо получить в результате исполнения алгоритма, то качество работы алгоритма будет характеризовать функция ![]() , оценивающая величину рассогласования между требуемыми
, оценивающая величину рассогласования между требуемыми ![]() и полученными выходными значениями алгоритма
и полученными выходными значениями алгоритма ![]() при данных входных значениях. Кроме того, функция
при данных входных значениях. Кроме того, функция ![]() может оценивать не только точность, но и сложность получаемого алгоритма (например, время выполнения, число итераций, сложность (длину) формул).
может оценивать не только точность, но и сложность получаемого алгоритма (например, время выполнения, число итераций, сложность (длину) формул).
Таким образом, проблема синтеза алгоритма состоит в следующем: для данного темплейта ![]() и заданных наборов значений входных-выходных параметров
и заданных наборов значений входных-выходных параметров ![]() ,
, ![]() , необходимо найти такие значения параметров
, необходимо найти такие значения параметров ![]() и функций
и функций ![]() темплейта
темплейта ![]() , определяющие алгоритм
, определяющие алгоритм ![]() , что
, что
![]()
для всех ![]() , при любых других значениях параметров
, при любых других значениях параметров ![]() и функций
и функций ![]() .
.
Для решения данной проблемы в работе рассматривается основанный на темплейтах многовариантный эволюционный алгоритм (Template-based Multi-variant Evolutionary Synthesis - TМES) для автоматизированного синтеза (открытия) алгоритмов, оптимизирующих заданный критерий качества ![]() . Этот подход основан на интеграции генетических алгоритмов (ГА) [4] и модификации метода генетического программирования (ГП) [5] с использоварием представления особей множеством выражений (MultiExpression Programming - MEP)[6] и позволяет получить новые свойства, не имеющиеся у исходных компонентов (меньшее время исполнения и синтез алгоритмов с большей циклической сложностью и наличием рекурсивных функций, по сравнению с ГР, и синтез новых функций и предикатов, что достаточно трудно при ГА).
. Этот подход основан на интеграции генетических алгоритмов (ГА) [4] и модификации метода генетического программирования (ГП) [5] с использоварием представления особей множеством выражений (MultiExpression Programming - MEP)[6] и позволяет получить новые свойства, не имеющиеся у исходных компонентов (меньшее время исполнения и синтез алгоритмов с большей циклической сложностью и наличием рекурсивных функций, по сравнению с ГР, и синтез новых функций и предикатов, что достаточно трудно при ГА).
Эти свойства данного подхода основаны на предварительном знании прикладной области и выборе обобщенной вычислительной схемы алгоритма, задаваемой в виде темплейта. Традиционное генетическое программирование страдает от слабо-ограниченного слепого поиска в огромных пространствах параметров для реальных прикладных проблем и имеет большие временные затраты. В данной работе исследуется использование темплейтов алгоритмов для ограничения пространства поиска к допустимым моделям и структурам решений. Этот подход представляет гибкий и прямой путь включения знаний эксперта относительно параметров, функций и структуры решаемой проблемы в разрабатываемую вычислительную модель алгоритма. В предельных случаях, с одной стороны, если мы не знаем темплейт искомого алгоритма, данный подход дает нам традиционное генетическое программирование. С другой стороны, если мы знаем полную структуру алгоритма и не знаем только некоторые его параметры, данный подход дает нам традиционный генетический алгоритм для поиска оптимальных параметров. Примером такой параметрической оптимизации на основе заданного темплейта с помощью генетического алгоритма служит алгоритм предназначенный для открытия аналитических описаний новых плотных семейств оптимальных регулярных сетей, представленный в [3]. Отметим, что используемый многовариантный алгоритм эволюционного синтеза, в отличии от стандартного алгоритмагенетического программирования, (1) является гибридным (ГП+ГА), (2) имеет два вида хромосом – линейные (для ГА) и последовательность инструкции (для ГП), и, соответственно, обобщенный (для двух видов) набор генетических операторов, (3) основан на использовании темплейтов с различной степенью специализации (в отличии от стандартного ГП, где поиск функции начинается «с нуля»), (4) позволяет осуществлять поиск заданного множества неизвестных функций и параметров темплейта, (5) использует многовариантное представление особей множеством выражений для каждой функции. Для выбора темплейта есть несколько способов: (1) знания и интуиция эксперта-исследователя, имеющего некоторую модель процесса или объекта, включающую неизвестные функции и параметры, (2) некоторые библиотеки темплейтов (шаблонов, скелетонов), например, из [1-3], (3) некоторые системы индуктивного вывода, позволяющие получить предварительную (недоопределенную) схему алгоритма, используемую как темплейт.
В первой части работы будет представлено краткое описание алгоритма многовариантного эволюционного синтеза, во второй части - получены оценки трудоемкости данного алгоритма, показано влияние степени специализации шаблона на пространство поиска, проведено сравнение с ранее предложенным стандартным (простым) методом эволюционного синтеза [7] и показано значительное (в несколько раз) сокращение времени поиска при использовании многовариантногоэволюционного алгоритма синтеза.
1. Алгоритм многовариантного эволюционного синтеза.
Алгоритм многовариантного эволюционного синтеза основан на эволюционных вычислениях и моделировании процесса естественного отбора популяции особей, каждая из которых представлена точкой в пространстве решений задачи оптимизации. Особи представлены структурами данных ![]() (хромосомами), включающими недоопределенные параметры
(хромосомами), включающими недоопределенные параметры ![]() и функции (формулы)
и функции (формулы) ![]() темплейтов, необходимые для построения заданного алгоритма
темплейтов, необходимые для построения заданного алгоритма ![]() на основе выбранного темплейта
на основе выбранного темплейта ![]() :
: ![]()
![]()
![]() Каждая популяция является множеством структур данных
Каждая популяция является множеством структур данных ![]() и определяет множество алгоритмов
и определяет множество алгоритмов ![]() , образующихся из данного темплейта
, образующихся из данного темплейта ![]() .
.
Основная идея алгоритма синтеза состоит в эволюционном преобразовании множества хромосом (параметров и формул темплейта) в процессе естественного отбора с целью выживания "сильнейшего". В нашем случае этими особями являются алгоритмы, имеющие наименьшее значение целевой функции. Алгоритм начинается с генерации начальной популяции. Все особи в этой популяции создаются случайно, затем отбираются наилучшие особи и запоминаются. Для создания популяции следующего поколения (следующей итерации), новые особи формируются с помощью генетических операций селекции (отбора), мутации, кроссовера и добавления новых элементов (для сохранения разнообразия популяции).
Примем, что целевая функция (fitness function, функция качества, функция пригодности) ![]() вычисляет сумму квадратов отклонений выходных данных алгоритма
вычисляет сумму квадратов отклонений выходных данных алгоритма ![]() от заданных эталонных значений
от заданных эталонных значений ![]() для определенных наборов множества входных данных
для определенных наборов множества входных данных ![]() , :
, : 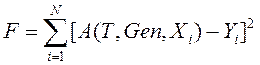 . Целью алгоритма является поиск минимума
. Целью алгоритма является поиск минимума ![]() . На практике, если получается несколько решений с одинаковым значением целевой функции, то выбиралось решение с меньшой оценкой структурной сложности, т.е. с меньшой общей длиной (суммой числа элементов) формул решения.
. На практике, если получается несколько решений с одинаковым значением целевой функции, то выбиралось решение с меньшой оценкой структурной сложности, т.е. с меньшой общей длиной (суммой числа элементов) формул решения.
Для представления и реализации основной структуры данных - хромосомы ![]() был предложен подход, основанный на комбинации линейной структуры хромосомы для параметров
был предложен подход, основанный на комбинации линейной структуры хромосомы для параметров ![]() (как в генетических алгоритмах [4]) и последовательной операторной структуры хромосомы для каждой из функций (формул)
(как в генетических алгоритмах [4]) и последовательной операторной структуры хромосомы для каждой из функций (формул) ![]() (как в генетическом программировании с использованием множества выражений [5]). Линейная структура хромосомы
(как в генетическом программировании с использованием множества выражений [5]). Линейная структура хромосомы ![]() используется для представления параметров
используется для представления параметров ![]() темплейта
темплейта ![]() : значения целочисленных и действительных коэффициентов и переменных, значения индексов, величины инкрементов и декрементов, а также знаков переменных, логических операций и отношений, типов округления переменных, например:
: значения целочисленных и действительных коэффициентов и переменных, значения индексов, величины инкрементов и декрементов, а также знаков переменных, логических операций и отношений, типов округления переменных, например: ![]() .
.
Операторные структуры в хромосоме ![]() используются для представления каждой из функций (формул)
используются для представления каждой из функций (формул) ![]() . Суть заключается в представлении функции интерпретируемым кодом, каждая операция которого будет считаться отдельной функцией. Первой операцией всегда будет инструкция вызова переменной данной функции. Выполнение происходит сверху вниз и аргументами инструкций могут выступать лишь записи, расположенные ранее, поэтому исполнение получается линейным. Генетическое решение, в этом случае, представляет сразу множество функций-выражений (последовательностями от первого до каждого текущего оператора), что позволяет, в отличии от стандартного ГП, оценить одновременно множество выражений, представленных операторной последовательностью и сократить время поиска оптимального решения. При этом, в качестве оценки данной хромосомы, из множества полученных вариантов выбирается оценка выражения с минимальным (максимальным) значением целевой функции. Переменные и константы формулы
. Суть заключается в представлении функции интерпретируемым кодом, каждая операция которого будет считаться отдельной функцией. Первой операцией всегда будет инструкция вызова переменной данной функции. Выполнение происходит сверху вниз и аргументами инструкций могут выступать лишь записи, расположенные ранее, поэтому исполнение получается линейным. Генетическое решение, в этом случае, представляет сразу множество функций-выражений (последовательностями от первого до каждого текущего оператора), что позволяет, в отличии от стандартного ГП, оценить одновременно множество выражений, представленных операторной последовательностью и сократить время поиска оптимального решения. При этом, в качестве оценки данной хромосомы, из множества полученных вариантов выбирается оценка выражения с минимальным (максимальным) значением целевой функции. Переменные и константы формулы ![]() образуют множество терминальные символов -
образуют множество терминальные символов - ![]() , а операции, используемые в формуле
, а операции, используемые в формуле ![]() , образуют множество нетерминальных символов -
, образуют множество нетерминальных символов - ![]() . Пусть
. Пусть ![]() , тогда
, тогда ![]() ,
, ![]() и пример представления данной функции в виде последовательной операторной структуры с интерпретируемым кодом показан в таблице 1, где N– номер операции, K - сама операция (инструкция), E - получаемое выражение (формула) для данной инструкции, F - значение целевой функции для каждой инструкции.
и пример представления данной функции в виде последовательной операторной структуры с интерпретируемым кодом показан в таблице 1, где N– номер операции, K - сама операция (инструкция), E - получаемое выражение (формула) для данной инструкции, F - значение целевой функции для каждой инструкции.
Таблица 1. Пример представления функции в виде последовательной операторной структуры.
N | K | E | F |
1 | x |
|
|
2 | 2 |
|
|
3 | + 1, 2 |
|
|
4 | a |
|
|
5 | * 4, 1 |
|
|
6 | 5 |
|
|
7 | - 5, 6 |
|
|
8 |
|
|
|
9 | / 3, 8 |
|
|
При создании хромосом ![]() порождаются последовательности инструкций (аналитические выражения) для функций
порождаются последовательности инструкций (аналитические выражения) для функций ![]() и задаются значения параметров
и задаются значения параметров ![]() , по которым можно производить оценивание и модификации алгоритма
, по которым можно производить оценивание и модификации алгоритма ![]() .
.
Таким образом, для фиксированных значений функций ![]() и параметров
и параметров ![]() мы можем вычислять алгоритмы
мы можем вычислять алгоритмы ![]() , порожденные на основе заданных темплейтов
, порожденные на основе заданных темплейтов ![]() и полученных в ходе эволюции хромосом
и полученных в ходе эволюции хромосом ![]() , для требуемых наборов множества входных данных
, для требуемых наборов множества входных данных ![]() .
.
Оператор мутации применяется к особям, случайно выбранным из текущей популяции с вероятностью ![]() [0,1]. Мутация линейной части хромосомы
[0,1]. Мутация линейной части хромосомы ![]() состоит в изменении значения случайно выбранного параметра
состоит в изменении значения случайно выбранного параметра ![]() на другую, случайно выбранную величину из множества допустимых значений. Мутация операторной части хромосомы
на другую, случайно выбранную величину из множества допустимых значений. Мутация операторной части хромосомы ![]() состоит в изменении значения оператора или операндов случайно выбранной инструкции в представлении функции
состоит в изменении значения оператора или операндов случайно выбранной инструкции в представлении функции ![]() на другую, случайно выбранную величину из множества допустимых значений. Оператор кроссовера (скрещивания) применяется к двум особям (родителям), случайно выбранным из текущей популяции с вероятностью
на другую, случайно выбранную величину из множества допустимых значений. Оператор кроссовера (скрещивания) применяется к двум особям (родителям), случайно выбранным из текущей популяции с вероятностью ![]() [0,1]. Кроссовер состоит в порождении двух новых особей путем обмена частями хромосом родителей (обмен подчастями линейных структур и обмен подпоследовательностями для операторных структур хромосомы
[0,1]. Кроссовер состоит в порождении двух новых особей путем обмена частями хромосом родителей (обмен подчастями линейных структур и обмен подпоследовательностями для операторных структур хромосомы ![]() ). Оператор создания нового элемента (особи) состоит в генерации случайных значений параметров
). Оператор создания нового элемента (особи) состоит в генерации случайных значений параметров ![]() и функций
и функций ![]() , описывающих алгоритмы. Это позволяет увеличить степень разнообразия особей при создании популяции. Оператор селекции (отбора) реализует принцип выживания наиболее приспособленных особей. Он выбирает наилучших особей с минимальными значениями целевой функции
, описывающих алгоритмы. Это позволяет увеличить степень разнообразия особей при создании популяции. Оператор селекции (отбора) реализует принцип выживания наиболее приспособленных особей. Он выбирает наилучших особей с минимальными значениями целевой функции ![]() . Отметим, что при оценке приспособленности особи для каждой инструкции решения рассматривается отдельная формула (выражение), и для нее вычисляется значение целевой функции (среднеквадратическое отклонение относительно эталонных данных). Оценка особи происходит по минимальному значению целевой функции среди всех выражений, представляющих ее.
. Отметим, что при оценке приспособленности особи для каждой инструкции решения рассматривается отдельная формула (выражение), и для нее вычисляется значение целевой функции (среднеквадратическое отклонение относительно эталонных данных). Оценка особи происходит по минимальному значению целевой функции среди всех выражений, представляющих ее.
Для поиска оптимума заданной целевой функции ![]() итерационный процесс вычислений в алгоритме эволюционного синтеза организован следующим образом.
итерационный процесс вычислений в алгоритме эволюционного синтеза организован следующим образом.
Первая итерация: порождение начальной популяции. Все особи популяции создаются с помощью оператора новый элемент, с проверкой и отсеиванием всех непригодных особей. После заполнения массива популяции лучшие особи отбираются и запоминаются в массиве best. Промежуточная итерация: шаг от текущей к следующей популяции. Основной шаг алгоритма состоит в создании нового поколения особей на основе массива best, используя операции селекции, мутации, кроссовера и добавления новых элементов. После оценки целевой функции для каждой особи в поколении проводится сравнение величин этих функций с величинами целевых функций тех особей, которые сохранены в массиве best. В том случае, если элемент из нового поколения лучше, чем элемент best [i], для некоторого i, помещаем новый элемент на место i в массив best и сдвигаем в нем все остальные элементы на единицу вниз. Таким образом, лучшие элементы локализуются в верхней части массива best. Последняя итерация (критерий остановки): итерации заканчиваются либо после исполнения заданного числа шагов, либо после нахождения оптимального алгоритма ![]() .
.
После выполнения алгоритма синтеза, мы получаем алгоритм ![]() , имеющий минимальное среднеквадратическое отклонение выходных данных от заданных эталонных значений
, имеющий минимальное среднеквадратическое отклонение выходных данных от заданных эталонных значений ![]() для определенных наборов множества входных данных
для определенных наборов множества входных данных ![]() .
.
2. Экспериментальные результаты.
Алгоритм эволюционного синтеза на основе темплейтов был успешно применен для автоматизированного получения (открытия) следующих алгоритмов: алгоритм Евклида, вычисления наибольшего общего делителя двух целых чисел, вычисления степени и факториала натурального числа, определения минимального (максимального) элемента массива, определения суммы квадратов элементов массива, вычисления скалярного произведения векторов, определение рекурсивных формул последовательностей Фибоначчи и Трибоначчи, вычисления суммы двух матриц, рекурсивных алгоритмов сортировки методом пузырька, слияния и Шелла, алгоритмов вычисления корней уравнений, параллельных алгоритмов балансировки нагрузки в многопроцессорных системах, алгоритмов определения минимального покрывающего дерева и кратчайших путей в графе. Данный подход был также применен для открытия аналитических описаний новых плотных семейств оптимальных регулярных сетей [8] и функции расстояния для циркулянтных графов степени 4, для оптимизации торговых стратегий на финансовых рынках, для синтеза рекурсивных функций для операций работы со списками и для решения математических задач определения членов последовательностей из IQ теста (теста коэффициента интеллектуальности).
Эволюционный многовариантныйсинтез алгоритмов на основе темплейтов реализован на языке программирования C, темплейты также задаются на этом языке.
Проведем сравнение эффективности поиска для простого [7] и многовариантного эволюционных методов синтеза. При реализации алгоритма эволюционного синтеза основную трудность представляет поиск неопределённых функций с помощью генетического программирования. В этом случае, время вычисления выражения, представленного последовательностью инструкций длинной ![]() операторов равно
операторов равно ![]() где
где ![]() - среднее время выполнения одного оператора. При многовариантном методе мы получаем
- среднее время выполнения одного оператора. При многовариантном методе мы получаем ![]() оценок целевой функции (для каждого оператора) при одном вычислении выражения, представленного последовательностью инструкций длинной
оценок целевой функции (для каждого оператора) при одном вычислении выражения, представленного последовательностью инструкций длинной ![]() операторов, а при простом методе только одну оценку для всего выражения. Т.к. основное время при эволюционном синтезе затрачивается на получение оценок целевой функции, то при использовании многовариантного эволюционного метода синтеза можно получить ускорение поиска решения порядка
операторов, а при простом методе только одну оценку для всего выражения. Т.к. основное время при эволюционном синтезе затрачивается на получение оценок целевой функции, то при использовании многовариантного эволюционного метода синтеза можно получить ускорение поиска решения порядка ![]() , где
, где ![]() - длинна последовательности операторов для представления выражения (функции). Обычно используется длинна последовательности операторов
- длинна последовательности операторов для представления выражения (функции). Обычно используется длинна последовательности операторов ![]() порядка
порядка ![]() . Для экспериментальной оценки получаемого ускорения при использовании многовариантного эволюционного метода синтеза приведем несколько примеров поиска различных функций.
. Для экспериментальной оценки получаемого ускорения при использовании многовариантного эволюционного метода синтеза приведем несколько примеров поиска различных функций.
Рассмотрим поиск полиномиальной функции ![]() при разной степени специализации темплейта. Число итераций и размер популяции выбраны экспериментально на основе параметров из [4, 5]. Значения основных параметров в экспериментах следующие: размер популяции – 100, число итераций – 30000, частота мутации – 0.15, частота кроссовера – 0.7, длинна последовательности операторов – 20.
при разной степени специализации темплейта. Число итераций и размер популяции выбраны экспериментально на основе параметров из [4, 5]. Значения основных параметров в экспериментах следующие: размер популяции – 100, число итераций – 30000, частота мутации – 0.15, частота кроссовера – 0.7, длинна последовательности операторов – 20.
Пусть заданы 8 пар вход - выход для ![]() и темплейт
и темплейт ![]() где
где ![]() - известный терм и
- известный терм и ![]() - известная часть функции (см. таблицу 2). Множество терминальных символов в этом случае
- известная часть функции (см. таблицу 2). Множество терминальных символов в этом случае ![]() , где
, где ![]() - элемент множества случайных натуральных чисел. Набор операций, используемый для синтеза формул, следующий:
- элемент множества случайных натуральных чисел. Набор операций, используемый для синтеза формул, следующий: ![]() . В таблице 2 приведены результаты сравнения характеристик алгоритмов на основе темплейтов простого эволюционного и многовариантного эволюционного методов синтеза - времени поиска решения
. В таблице 2 приведены результаты сравнения характеристик алгоритмов на основе темплейтов простого эволюционного и многовариантного эволюционного методов синтеза - времени поиска решения ![]() ,
,![]() (с), числа поколений
(с), числа поколений ![]() ,
,![]() до получения решения (соответственно для каждого метода), а также величину ускорения времени поиска решения
до получения решения (соответственно для каждого метода), а также величину ускорения времени поиска решения ![]() для многовариантного метода - при различных темплейтах. Для каждого темплейта приведены средние значения, полученные по результатам 100 экспериментов.
для многовариантного метода - при различных темплейтах. Для каждого темплейта приведены средние значения, полученные по результатам 100 экспериментов.
Таблица 2. Сравнение характеристик алгоритмов эволюционного синтеза.
i | T |
|
|
|
|
|
1 |
| 43,03 | 19010 | 0,023 | 1,68 | 1871 |
2 |
| 0,076 | 38,53 | 0,0078 | 0,001 | 9,75 |
Из таблицы 2 видно, что применение многовариантного эволюционного метода синтеза позволяет получить значительное ускорение времени поиска (9,75 и 1870 раз для различных темплейтов). Отметим также, что увеличение степени специализации темплейта позволяет значительно уменьшить время поиска (на три порядка).
Рассмотрим поиск другой полиномиальной функции вида: ![]() при различной степени специализации темплейта. Пусть заданы 8 пар вход - выход для
при различной степени специализации темплейта. Пусть заданы 8 пар вход - выход для ![]() и темплейт
и темплейт ![]() где
где ![]() - известная часть функции, а
- известная часть функции, а![]() - неизвестная часть функции (см. таблицу 3). Множество терминальных символов в этом случае
- неизвестная часть функции (см. таблицу 3). Множество терминальных символов в этом случае ![]() , где
, где ![]() - элемент множества случайных натуральных чисел. Набор операций, используемый для синтеза формул, следующий:
- элемент множества случайных натуральных чисел. Набор операций, используемый для синтеза формул, следующий: ![]() . В таблице 3 приведены результаты сравнения характеристик алгоритмов на основе темплейтов Tпростого эволюционного и многовариантного эволюционного методов синтеза - времени поиска решения
. В таблице 3 приведены результаты сравнения характеристик алгоритмов на основе темплейтов Tпростого эволюционного и многовариантного эволюционного методов синтеза - времени поиска решения ![]() ,
,![]() (с), числа поколений
(с), числа поколений ![]() ,
,![]() до получения решения (соответственно для каждого метода), а также величину ускорения времени поиска решения
до получения решения (соответственно для каждого метода), а также величину ускорения времени поиска решения ![]() для многовариантного метода - при различных темплейтах. Для каждого темплейта приведены средние значения, полученные по результатам 100 экспериментов.
для многовариантного метода - при различных темплейтах. Для каждого темплейта приведены средние значения, полученные по результатам 100 экспериментов.
Таблица 3. Сравнение характеристик алгоритмов эволюционного синтеза.
i | T |
|
|
|
|
|
1 |
| 0,059 | 25,9 | 0,012 | 0,001 | 4,92 |
2 |
| 0,45 | 231,15 | 0,034 | 2,27 | 13,2 |
3 |
| 18,5 | 9321,4 | 1,56 | 211 | 11,9 |
4 |
| 48,4 | 24532,2 | 1,86 | 270 | 26 |
Из таблицы 3 видно, что применение многовариантного эволюционного метода синтеза позволяет получить значительное ускорение времени поиска (от 4,92 до 26 раз для различных темплейтов). Отметим также, что увеличение степени специализации темплейта позволяет в этом случае значительно уменьшить время поиска (в несколько раз).
Рассмотрим для примера поиск функции с тригонометрическими, показательными и экспоненциальными членами ![]() при различной степени специализации темплейта.
при различной степени специализации темплейта.
Пусть заданы 15 пар вход - выход для ![]() и темплейт
и темплейт ![]() где
где ![]() - неизвестная часть функции (см. таблицу 4). Множество терминальных символов в этом случае
- неизвестная часть функции (см. таблицу 4). Множество терминальных символов в этом случае ![]() , где
, где ![]() - элемент множества случайных натуральных чисел. Набор операций, используемый для синтеза формул, следующий:
- элемент множества случайных натуральных чисел. Набор операций, используемый для синтеза формул, следующий: ![]() . В таблице 4 приведены результаты сравнения характеристик алгоритмов на основе темплейтов простого эволюционного и многовариантного эволюционного методов синтеза - времени поиска решения
. В таблице 4 приведены результаты сравнения характеристик алгоритмов на основе темплейтов простого эволюционного и многовариантного эволюционного методов синтеза - времени поиска решения ![]() ,
,![]() (с), числа поколений
(с), числа поколений ![]() ,
,![]() до получения решения (соответственно для каждого метода), а также величину ускорения времени поиска решения
до получения решения (соответственно для каждого метода), а также величину ускорения времени поиска решения ![]() для многовариантного метода - при различных темплейтах. Для каждого темплейта приведены средние значения, полученные по результатам 100 экспериментов.
для многовариантного метода - при различных темплейтах. Для каждого темплейта приведены средние значения, полученные по результатам 100 экспериментов.
Таблица 4. Сравнение характеристик алгоритмов эволюционного синтеза.
i | T |
|
|
|
|
|
1 |
| 995,3 | 5000 | 113,7 | 14,4 | 8,75 |
2 |
| 696,6 | 292,6 | 46,6 | 5,5 | 14,95 |
3 |
| 150,5 | 31,9 | 8,7 | 0,4 | 17,3 |
4 |
| 2,55 | 11,7 | 1 | 0 | 2,55 |
Из таблицы 4 видно, что применение многовариантного эволюционного метода синтеза позволяет получить значительное ускорение времени поиска (от 2,5 до 17 раз для различных темплейтов). Отметим также, что увеличение степени специализации темплейта позволяет в этом случае значительно уменьшить время поиска (в несколько раз).
Рассмотрим влияние метода синтеза при поиске описания последовательности Маккея – Гласса (Mackey - Glass), имеющей в дискретной форме следующий вид: ![]() . Пусть заданы 100 пар вход - выход для
. Пусть заданы 100 пар вход - выход для ![]() множество терминальных символов
множество терминальных символов ![]() , множество примитивных функций
, множество примитивных функций ![]() . При использовании темплейта, выражающего зависимость от предыдущего и любого другого члена последовательности в виде
. При использовании темплейта, выражающего зависимость от предыдущего и любого другого члена последовательности в виде ![]() , где
, где ![]() - действительные,
- действительные, ![]() - целые числа, получаем точную формулу последовательности Маккея – Гласса в случае простого эволюционного метода синтеза при числе поколений
- целые числа, получаем точную формулу последовательности Маккея – Гласса в случае простого эволюционного метода синтеза при числе поколений ![]() =801 и времени поиска решения
=801 и времени поиска решения ![]() = 905 с., а в случае многовариантного эволюционного метода синтеза при числе поколений
= 905 с., а в случае многовариантного эволюционного метода синтеза при числе поколений ![]() =194 и времени поиска решения
=194 и времени поиска решения ![]() = 65,3 с., т.е. ускорение времени поиска при многовариантном эволюционном методе составляет
= 65,3 с., т.е. ускорение времени поиска при многовариантном эволюционном методе составляет ![]() =14,25.
=14,25.
Заключение.
Дано описание многовариантного эволюционного метода синтеза, объединяющего преимущества генетических алгоритмов и генетического программирования, основанного на последовательной операторной структуре хромосомы, темплейтах (шаблонах, скелетонах) алгоритмов и заданном множестве пар входных - выходных данных. Проведено исследование влияния множества оценок хромосомы и степени специализации темплейта на характеристики алгоритма поиска при эволюционном синтезе. Получены оценки трудоемкости данного алгоритма, проведено сравнение со стандартным методом эволюционного синтеза и показано значительное (в несколько раз) сокращение времени поиска при использовании многовариантногоэволюционного алгоритма синтеза.
Список литературы
1. Cole M. Algorithmic Skeletons: Structured Management of Parallel Computation. Cambridge: The MIT Press, 1989. 131 p.
2. Watanobe Y., Mirenkov N., Yoshioka R., Monakhov O. Filmification of methods: A visual language for graph algorithms // Journal of Visual Languages and Computing. 2008. Vol. 19, no. 1. P. 123-150. http://dx.doi.org/10.1016/j.jvlc.2006.09.003
3. Gamma E., Helm R., Johnson R., Vlissides J. Design Patterns: Elements of Reusable Object-Oriented Software. Addison-Wesley, Reading, MA, 1994. 416 p.
4. Goldberg D.E. Genetic Algorithms, in Search, Optimization and MachineLearning. Addison-Wesley, Reading, MA, 1989.
5. Koza J. Genetic Programming. Cambridge: MIT Press, 1992.
6. Oltean M. Multi Expression Programming. Technical Report. Babes-Bolyai Univ., Romania, 2006.
7. Монахов О.Г. Эволюционный синтез алгоритмов на основе шаблонов // Автометрия. 2006. Т. 42, № 1. С. 116-126.
8. Monakhov O.G., Monakhova E.A. An Algorithm for Discovery of New Families of Optimal Regular Networks // Proc. of 6th Inter. Conf. on Discovery Science (DS 2003). Sapporo, Japan, LNAI, N2843, Springer-Verlag, Berlin Heidelberg, 2003. P. 244-254.
Публикации с ключевыми словами: скелетон, шаблон, генетический алгоритм, генетическое программирование, эволюционный синтез, темплейт
Публикации со словами: скелетон, шаблон, генетический алгоритм, генетическое программирование, эволюционный синтез, темплейт
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



