научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2013
DOI: 10.7463/0113.0547731
УДК 004.3 +519.6
Россия, МГТУ им. Н.Э. Баумана
Введение
Ультраграф является перспективной моделью объектов при решении таких задач как потоковый анализ и синтез, синтез структур высокого уровня сложности [1]. Эти задачи имеют, как правило, высокую размерность входа, а программы их решения характеризуются большой временной сложностью.
В работах [2, 3, 4, 5, 6, и др.] рассмотрен ряд методов и приёмов снижения вычислительной сложности алгоритмов на множествах и графах. Одним из наиболее эффективных методов снижения последней является сокращение времени выполнения основных операций, производимых над ультраграфами. Однако авторам не известны работы, посвящённые исследованию оптимизирующих преобразований алгоритмов операций над ультраграфами.
Целью исследования является экспериментальная оценка эффективности способов снижения временной сложности алгоритмов операций над ультраграфами. В теоретической части показано, что наибольший вклад в вычислительную сложность алгоритма операции добавления вершины в ультраграф вносят копирование множеств и формирование множеств образов и прообразов вершин и ребер относительно предикатов смежности. Констатируется, что это характерно для всех операций над ультраграфами. На основе выполненного анализа выбраны используемые преобразования.
В разделе «экспериментальные исследования» даётся характеристика ультраграфа, на котором проводились исследования, Обсуждаются их результаты. Показана высокая эффективность применённых преобразований.
1 Теоретический анализ алгоритмов операций над ультраграфами
Операции над ультраграфами, соответствующие проектным процедурам над структурами сложных систем, в которых компоненты связаны не попарно, описаны в [7, 8]. Для выбора объекта исследования приведём алгоритм операции добавления вершины и результаты его анализа.
Обозначение операции:
HU1(X1,U1) = HU (X,U) + HUк(xk, {Uk+, Uk–}).
Здесь: xk добавляемая вершина; Uk+ =Г1xk – множество ребер, ей инцидентных;
Uk– =Г2xk – множество ребер, которым она инцидентна.
Порядок выполнения операции:
1. Создаем множества X1, Г1X1 и Г2X1:
X1 = X . xk; Г1X1 = Г1X.Г1 xk; Г2X1 = Г2 X.Г2 xk.
2. Копируем множество Uпод именем U1:
U1 = U.
3. Определяем множество образов ребер Г2U1, занося в него Г2uj из множества Г2U, если ребро uj не принадлежит Uk–, и добавляя вершину xk в образы тех ребер, которым она инцидентна:
![]()
4. Формируем множество прообразов ребер Г1U1, занося в него Г1ujиз множества Г1U, если ребро uj не принадлежит Uk+, и добавляя вершину xk в образы тех ребер, которые ей инцидентны.
![]()
5. Создаем множество образов F1X1 вершин относительно предиката смежности F1, занося F1xiиз F1X, если вершина xk не инцидентна ребрам, которые принадлежат образу Г1xiвершины xi, и добавляя в F1xi вершину xk в противном случае. Определяем вершины, смежные добавляемой, и заносим их в F1X1.

где
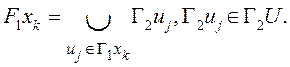
6. Формируем множество прообразов F1-1X1, занося F1-1xi из F1-1X, если вершине xkне инцидентны ребра прообраза Г2xi, и добавляя в F1-1xiвершину xkв противном случае. Определяем вершины прообраза F1-1xkи заносим его в множество F1-1X1.
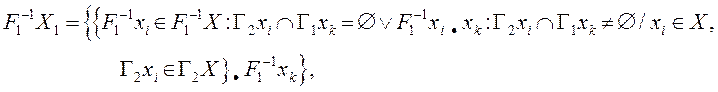
где
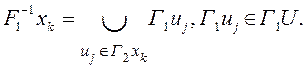
7. Определяем множество образов ребер F2U1, копируя в него F2uj из F2U, если ребро ujне принадлежит Uk–. В противном случае добавляем в F2uj не принадлежащие ему ребра множества Uk+.
![]()
8. Формируем множество прообразов ребер F2–1U1, копируя в него F2–1uj из F2–1U, если ребро uj не принадлежит Uk+. В противном случае добавляем в F2–1uj не принадлежащие ему ребра множества Uk–.
![]()
Асимптотическая оценка вычислительной сложности операции базируется на мерах сложности формирования множеств аналитического представления ультраграфа. Для её определения подсчитывается количество операций сравнения и копирования в функции от мощности обрабатываемых множеств, считая при этом, что вычислительные сложности этих операций одинаковы. Выполним такой подсчет на примере формирования множества образов ребер:
![]()
– проверка условия uj ∉ Г2xk требует максимум |Г2xk| сравнений,
– при благоприятном исходе выполняется копирование |Г2uj| элементов,
– количество благоприятных исходов равно |U1| – |Г2xk|,
– количество противоположных исходов равно |Г2xk| и при каждом таком исходе происходит копирование |{Г2uj· xk}| элементов. Будем считать, что при любом исходе копируется |Г2xk| элементов. Отсюда суммарное количество операций будет
(|Г2xk| + |Г2uj|) ´ (|U1| – |Г2xk|) + |Г2xk| ´ |Г2uj|.
Оценки сложности формирования множеств аналитического представления ультраграфа приведены в таблице 1. В ней использованы обозначения n= |X| и m= |U|.
Таблица 1 – Оценки сложности формирования множеств при выполнении операции добавления вершины
N п/п | Формируемые множества | Количество операций сравнения и копирования в функции от мощности обрабатываемых множеств | Мера сложности формирования множества |
1.1. | X1 | |X|= n | О(n) |
1.2. | Г1X1 | |Г1X|+|Г1xi| | О(n) или О(m), если |Г1xi| ≤ m, О(n), если |Г1xi| = const* |
1.3. | Г2X1 | |Г2X|+|Г2xi| | О(n) или О(m), если |Г2xi| ≤ m, О(n), если |Г2xi| = const |
2. | U1 | |U|= m | О(m) |
3. | Г2U1 | (|Г2xk |+ |Г2uj|) ´ (|U1| - |Г2xk |) + |Г2xk | ´ |Г2uj| | О(m×n), если |Г2xk| = const и |Г2uj |≤ n, О(m), если |Г2xk | и |Г2uj| = const |
4. | Г1U1 | (|Г1xk | + |Г1uj|) ´ (|U1| - |Г1xk |) + |Г1xk | ´ |Г1uj| | О(m×n), если |Г1xk| = const и |Г1uj|≤ n, О(m), если |Г1xk| и |Г1uj| = const |
5. | F1X1 | (|Г1xi|´|Г2xk | + |F1xi|) ´|X| | О(m2×n), если |Г1xi| и |Г2xk | ≤ m, О(n), если |Г1xi|, |Г2xk | и |F1xi| = const |
6. | F1-1X1 | (|Г2xi| ´ |Г1xk| + |F1-1xi|) ´ |X| | О(m2×n), если |Г2xi| и |Г1xk| ≤ m, О(n), если |Г2xi|, |Г1xk| и |F1-1xi|=const |
7. | F2U1 | (|Г2xk | + |F2uj|) ´ (|U1| - |Г2xk |) + (|Г2xk | + |F2uj| ´ |Г1xk |) ´ |Г2xk | | О(m3), если |Г2xk |, |Г1xk |и |F2uj| ≤ m, О(m), если |Г2xk |, |Г1xk| и |F2uj|=const |
8. | F2-1U1 | (|Г1xk | + |F2-1uj|) ´ (|U1| - |Г1xk |) + (|Г1xk | + |F2-1uj| ´ |Г2xk |) ´ |Г1xk | | О(m3), если |Г1xk |, |Г2xk | и |F2-1uj|≤m, О(m), если |Г1xk|,|Г2xk| и |F2-1uj|=const |
Отсюда следует, что асимптотическая оценка вычислительной сложности для данной операции над ультраграфом равна:
- в худшем O(m3) при m>n, если |Г2xk |, |Г1xk | и |F2uj| или |Г2xk|, |Г1xk | и |F2–1uj| ограничены величиной m, и O(m2n) при n>m, если |Г2xk | и |Г1xi| или |Г1xk | и |Г2xi| ограничены величиной m.
- в лучшем O(m) при m>n или O(n) при n>m, если мощности образов и прообразов вершин и ребер ограничены константой.
Из таблицы видно, что наибольший вклад в вычислительную сложность операции вносят операции копирования и процедуры формирования множеств образов и прообразов вершин и ребер относительно предикатов смежности. Как показывает анализ описаний алгоритмов [7, 8], эти процедуры присутствуют во всех операциях над ультраграфами. Поэтому достаточно исследовать одну операцию, например добавление вершины в ультраграф.
В таблице 2 показано несколько видов оптимизирующих преобразований (в том числе над упорядоченными множествами [9]) и оценка их вклада в снижение вычислительной сложности алгоритмов [10].
Таблица 2 – Оптимизирующие преобразования и их вклад в снижение вычислительной сложности
Оптимизирующее преобразование | Описание оптимизирующего преобразования | Вклад в снижение вычислительной сложности |
1. Замена операции копирования на присваивание указателя | В участках программы, где множеству присваиваются все элементы другого множества, цикл копирования элементов заменяется присваиванием указателя на структуру, содержащую в себе элементы этого множества. | Высокий |
2. Исключение лишних проверок при вычислении выражения Г1xi Г1xi Г2xi Г2xi | Замена полного перебора вершин для пересечения двух множеств на попарное сравнение элементов двух множеств и копированием с последующим их сдвигом при равенстве ключей или сдвигом элементов с меньшим ключом до первого их совпадения | Существенный, при большой мощности множеств образов и прообразов вершин и ребер относительно предикатов инцидентности. |
3. Исключение лишних проверок при вычислении выражения F2uj F2-1uj | Замена полного перебора вершин для объединения двух множеств на попарное сравнение элементов множеств и копированием элемента с меньшим ключом с последующим его сдвигом или сдвигом элементов каждого из множеств при равенстве ключей. | Существенный, при большой мощности множеств образов и прообразов ребер и вершин относительно предикатов смежности и инцидентности соответственно. |
2 Реализация и экспериментальные исследования
Известно, что время выполнения алгоритма существенно зависит от выбора структур данных, с которыми он оперирует [5, 11]. Для экспериментальной оценки вычислительной сложности операции добавления вершины в ультраграф было использовано матричное и аналитическое представление ультраграфа. При аналитическом представлении для возможности использования преобразования «замена операции копирования на присваивание указателя» образы и прообразы вершин и рёбер реализованы структурой «вектор списков».
Для проведения натурных экспериментов был разработан программный комплекс, включающий в себя описание классов структур данных для матричного и аналитического представления ультраграфов, а также методы, реализующие операцию добавления вершины в ультраграф.
Измерения проводились для ультраграфа с мощностями множества вершин и множества ребер n = m = 1000. Множества аналитического представления ультраграфа генерировались с помощью датчика случайных чисел с использованием соотношений:

где ρ+(xi) = |Г1xi| и ρ-(xi) = |Г2xi| – количество рёбер, инцидентных вершине xi, и количество рёбер, которым она инцидентна, A+(uj) = |Г2uj| и A-(uj) = |Г1uj| – количество вершин, инцидентных ребру uj, и количество вершин, которым оно инцидентно. Значения указанных параметров менялось в диапазоне 1 ≤ ρ+(xi) + ρ-(xi) ≤ 100 и 2 ≤ A+(uj) + A-(uj) 1 ≤ 100.
Количество измерений для оценки времени выполнения операции в каждом случае составляло 100 повторений, результаты измерений усреднялись. При этом среднеквадратичное отклонение не превышало 7–10 % от среднего значения.
На рисунке 1 показан вклад в снижение вычислительной сложности разных видов оптимизирующих преобразований при представлении образов и прообразов вершин и рёбер ультраграфа вектором списков и различных значениях мощности множеств образов и праобразов вершин и ребер (один, десять и пятьдесят процентов от n=m=1000). Оценка выигрыша от оптимизации произведена в процентах с использованием соотношения:
[(tнеопт – tоптi) / tнеопт] 100%
где tнеопт – время выполнения операции без применения оптимизирующих преобразований, tоптi – время выполнения операции с применением i-го оптимизирующего преобразования.
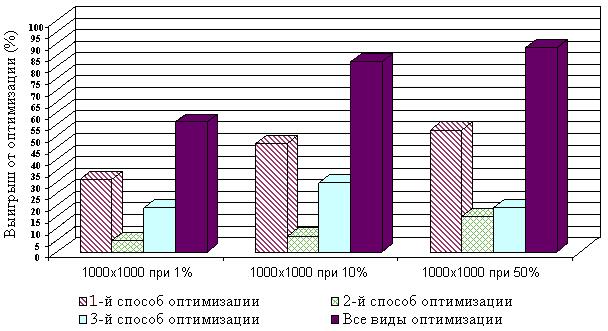
Рисунок 1 – Вклад оптимизирующих преобразований в снижение вычислительной сложности при представлении множеств аналитического задания ультраграфа вектором списков
Как видно из данных, представленных на рисунке 1, наибольший эффект дает применение оптимизирующего преобразования 1-го вида, что можно объяснить исключением большого количества операций копирования элементов множеств во всех пунктах алгоритма. Суммарный выигрыш от применения описанных выше оптимизирующих преобразований составил в ряде случаев от 53 до 87 % от исходного времени выполнения операции добавления вершины в ультраграф. Больший вклад третьего оптимизирующего преобразования по сравнению с вторым объясняется тем, что как правило, |F2uj | > |Г1xk| и |F2-1uj| > |Г2xk| в пределе в |Г2uj| раз.
Эффективность и возможность применения использованных для оценки оптимизирующих преобразований напрямую зависит от выбранной структуры представления данных. Так, например, при матричном представлении ультраграфа невозможно применить преобразование 1, а преобразования 2 и 3 сводятся к попарному сравнению элементов строк таблиц истинности соответствующих двуместных и одноместных предикатов. Например, при определении Г1xi ![]() Г2xk выполняется попарное сравнение элементов i-ой строки матрицы истинности двуместного предиката Г1(X, U) – «вершинам множества Xинцидентны рёбра множества U» с элементами характеристического вектора одноместного предиката Г2xk(U) «рёбра множества U, которым инцидентна вершина xk».
Г2xk выполняется попарное сравнение элементов i-ой строки матрицы истинности двуместного предиката Г1(X, U) – «вершинам множества Xинцидентны рёбра множества U» с элементами характеристического вектора одноместного предиката Г2xk(U) «рёбра множества U, которым инцидентна вершина xk».
На рисунке 2 показаны значения времени выполнения операции добавления вершины для матричного и аналитического представления ультраграфа при различных значениях мощности множеств образов и прообразов вершин и рёбер (1 % и 10 % от n = m = 1000).

Рисунок 2 – Зависимость времени выполнения операции добавления вершины к ультраграфу от структуры данных и связности ультраграфа
Зависимость на рисунке 2 показывает, что матричное представление ультраграфа не эффективно при низкой связности ультраграфа. Для ультраграфов с большими значениями мощности множеств образов и прообразов, время выполнения операций при матричном представлении достаточно близко по значению к оптимизированным операциям при использовании вектора списков. Однако следует иметь в виду, что использование матриц ограничено размером адресного пространства оперативной памяти.
Заключение
На основании выполненных исследований можно утверждать, что использованные оптимизирующие преобразования обеспечивают существенное сокращение времени выполнении операций над ультраграфами. Такие преобразования целесообразно применять при разработке алгоритмов, в которых копируются множества большой мощности и многократно выполняются операции над ними.
Полученные результаты позволяют сделать предположение о перспективности дальнейших исследований в области разработки и оценки эффективности оптимизирующих преобразований алгоритмов на множествах и графах.
Список литературы
1. Овчинников В.А. Математические модели объектов задач структурного синтеза // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2009. № 3. Режим доступа: http://technomag.edu.ru/doc/115712.html (дата обращения 25.01.2013).
2. Ахо А.В., Хопкрофт Д., Ульман Д.Д. Структуры данных и алгоритмы: пер. с англ. М.: Вильямс, 2001. 384 с.
3. Гудман С., Хидетниеми С. Введение в разработку и анализ алгоритмов: пер. с англ. М.: Мир, 1981. 368 с.
4. Новиков Ф. А. Дискретная математика для программистов. СПб: Питер, 2001. 304 c.
5. Овчинников В.А. Алгоритмизация комбинаторно-оптимизационных задач при проектировании ЭВМ и систем: учеб. для вузов. М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. 288 с.
6. Касьянов В.Н. Оптимизирующие преобразования программ. М.: Наука. Гл. ред. физ.-мат. лит., 1988. 336 с.
7 Овчинников В.А. Операции над ультра- и гиперграфами для реализации процедур анализа и синтеза структур сложных систем. Часть 2 // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2009. № 11. Режим доступа: http://technomag.edu.ru/doc/133223.html (дата обращения 25.01.2013).
8. Овчинников В.А. Операции над ультра- и гиперграфами для реализации процедур анализа и синтеза структур сложных систем. Часть 3 // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2009. № 12. Режим доступа: http://technomag.edu.ru/doc/134335.html (дата обращения 25.01.2013).
9. Овчинников В.А. Операции над упорядоченными множествами // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2011. № 6. Режим доступа: http://technomag.edu.ru/doc/188322.html (дата обращения 25.01.2013).
10. Овчинников В.А., Иванова Г. С. Оценка эффективности применения операций над упорядоченными множествами // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2011. № 10. Режим доступа: http://technomag.edu.ru/doc/239406.html (дата обращения 25.01.2013).
11. Иванова Г.С., Пасечников К.А. Синтез оптимальных структур данных для решения задач на графах // Вестник МГТУ имени Н.Э. Баумана. Сер. Приборостроение. 2008. № 4 (73). C. 29-38.
Публикации с ключевыми словами: алгоритм, эффективность, операции над ультраграфами, вычислительная (временная) сложность, оптимизирующие преобразования
Публикации со словами: алгоритм, эффективность, операции над ультраграфами, вычислительная (временная) сложность, оптимизирующие преобразования
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



