научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2013
DOI: 10.7463/0313.0546388
УДК 003.26
Россия, МГТУ им. Н.Э. Баумана
Построение криптографических поточных шифров основано на использовании генератора ключевого потока. Такой генератор с помощью ключа формирует ключевой поток, затем ключевой поток комбинируется определенным образом с исходным сообщением с целью получения зашифрованного сообщения. Отправитель передает зашифрованное сообщение законному получателю, который, имея ключ, формирует ключевой поток,и расшифровывает сообщение.
Согласно результатам исследований [6] при значениях параметров ключевого потока больше чем 4, атаки поточных шифров становятся неэффективными. В данной работе проведен анализ ключевого потока поточного шифра с помощью решения системы алгебраических уравнений при известных некоторых данных и найдены максимальные параметры генератора ключевого потока, при которых поточный шифр поддается анализу программными средствами.
Криптосистема или шифр – это кортеж из пяти элементов (Ƥ,C, Ҟ,E,D), таких что [3]:
- Ƥ – конечное множество исходных текстов;
- С - конечное множество шифротекстов;
- Ҟ - конечное множество символов ключевого потока;
- E : Ҟ×P->C алгоритм кодирования;
- D : Ҟ×С->P алгоритм декодирования;
Для любого K ϵ Ҟ, выполняется D(K,E(K,P)) = P для всех P ϵ Ƥ.
Поточные шифры преобразуют исходный текст в шифротекст по одному биту за операцию. Разновидность поточного шифра – схема одноразового блокнота. Для схемы одноразового блокнота Ƥ = C = Ҟ = {0,1}n, при n ≥ 1, алгоритм кодирования EK(P) = K⊕P, где ⊕− операция покомпонентного XOR, алгоритм декодирования DK(C) = K⊕C. Доказано, что схема одноразового блокнота обладает абсолютной криптографической стойкостью, если Kиспользуется один раз и выбран из {0,1}n [2]. Таким образом, если злоумышленник знает только C, он не сможет получить какую-либо информацию о P или K, даже при наличии неограниченных времени, памяти и вычислительных ресурсов.
Работа посвящена анализу поточного шифра, созданного с помощью схемы одноразового блокнота. Генератор ключевого потока инициализируют ключом меньшего размера, чем сам ключевой поток. Генератор ключевого потока вырабатывает псевдослучайный поток битов длины, равной длине исходного текста; создается псевдослучайная ключевая последовательность. Для анализа шифротекста в этом случае необходимо знать ключ и сгенерировать ключевой поток, использованный при шифровании. Выполнив покомпонентный XOR ключевого потока и шифротекста, можно получить исходное сообщение.
Генератор ключевого потока состоит из следующих компонентов [2]:
- внутренне состояние;
- Ҟ - конечное множество возможных внутренних состояний;
- функция обновления Y: Ҟ-> Ҟ;
- конечное множество Z, называемое алфавитом ключевого потока;
- функция выхода f : Ҟ -> Z.
Внутреннее состояние S0 ϵ Ҟ инициализируют ключом (или начальным состоянием), затем выполняют следующие операции:
- выходной бит zt ϵ Z вычисляется как zt = f(St);
- внутреннее состояние обновляется St+1 = Y(St).
Такт – это период времени, в течение которого выполняются две вышеперечисленные операции. В такте t производится выходной бит zt и St меняется на St+1.
Поточный шифр,основанный на генераторе ключевого потока - это совокупность кортежа (Ƥ, C, Ҟ, Z, E, D) и генератора ключевого потока, где [6]:
Ƥ – конечное множество, называемое алфавитом исходного текста;
С - конечное множество, называемое алфавитом шифротекста;
Ҟ – конечное множество возможных ключей;
Z - конечное множество, называемое алфавитом ключевого потока;
E : Z×P->C алгоритм кодирования;
D : Z×С->P алгоритм декодирования.
Генератор ключевого потока использует ключ K ϵ Ҟ для генерации последовательности z0, z1, z2, ...,называемой ключевым потоком произвольной длины, где zt ϵ Z для всех t ≥ 0. Для каждогоz ϵ Z, выполняется D(z,E(z,P)) = P для всех P ϵ Ƥ.
Получатель и отправитель взаимодействуют следующим образом:
- получатель и отправитель обмениваются секретным ключом K ϵ Ҟ по секретному каналу, секретный канал используют для передачи всех необходимых данных;
- пусть P = (p0, p1,p2,…) – исходный текст, где pt ϵ Ƥ. Отправитель использует K и генератор ключевого потока для создания ключевого потока z0, z1, z2,… и кодирует P в шифротекст C = (c0, c1,c2,…), где ct = Ezt(pt), затем посылает С получателю через общедоступный канал;
- получатель, зная секретный ключ, формирует у себя ключевой поток z0, z1,z2,…;
- получатель, используя ключевой поток z0, z1,z2,… декодирует pt = Dzt(ct).
Пусть F – конечное поле; регистр сдвига с линейной обратной связью (РСЛОС) длины n содержит внутреннее состояние размерности n и функцию обратной связи
![]()
В каждом такте определенный элемент внутреннего состояния становится выходным битом и внутреннее состояние изменяется на новое с помощью Λ. Пусть S0 = (z0,…, zn) ϵ Fn является начальным состоянием и L(x1,…, xn) = (x2,…, xn, Λ(x1,…, xn)) [2]. Схематичный вид РСЛОС представлен на рисунке 1. В каждый такт выполняются две операции[3]:
- на выход подается определенный элемент;
- изменение St на St+1 с помощью функции L:
![]()
ФункциюL можно идентифицировать с матрицей:

ПриэтомSt+1 = St·LL, атакжеSt = S0 · LLt. Матрица LL называется матрицей обратной связи [2].
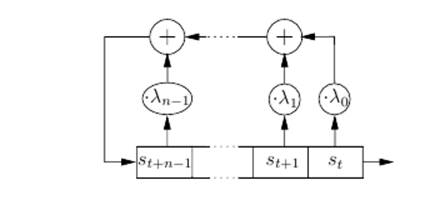
Рисунок 1 − РСЛОС.
В качестве генератора ключевого потока при создании поточного шифра использован (l,m)-комбайнер. Пусть F – конечное поле, (l,m)-комбайнер состоит из следующих шести компонентов [2]:
- s РСЛОС c длинами n1,…,nS и матрицами обратной связи L1,…,LS;
- внутреннее состояние S ϵ Fm× Fn, где n = n1+…+nS;
- матрица L, размером n×n, над полем F, определена как

- матрица проекций P, размером n×l, над полем F;
- функция изменения состояния памяти Ψ : Fm×Fl → Fm;
- функция выхода f : Fm×Fl → F.
Если m ≥ 1, тогда комбайнер называется комбайнером с памятью, а при m = 0 − простым комбайнером.
Внутреннее состояние (l,m)-комбайнера инициализируем значением: S0 = (Q0, K) ϵ Fm×Fn, гдеQ0 ϵ Fm – биты памяти, K = (K0,1,…, K0,S) ϵ Fn – начальные состояния s РСЛОС, где K0,i – начальное состояние i-го РСЛОС. Содержание РСЛОС обновляется с помощью матрицы L [2].
Во многих случаях используют только некоторые значения в состояниях РСЛОС для вычисления следующего элемента ключевого потока и следующего состояния памяти, определяемые матрицей проекции. Только значения из K · Lt · P вовлечены в вычисления на такте t. Обозначим Kt = K · Lt · P и назовем Kt− вход (l,m)-комбайнера. Обновление состояния памяти происходит через Qt+1 = Ψ(Qt, Kt), а элемент ключевого потока вычисляется как zt = f(Qt, Kt). Функция обновления ϒ(St) = ϒ(Qt, K · Lt) = (Ψ(Qt, K · Lt · P), K · Lt+1) [2]. Схематичный вид (l,m)-комбайнера показан на рисунке 2.

Рисунок 2 − (l,m)-комбайнер.
Найдем первоначальное состояние (ключ) (l,m)-комбайнера. Пусть Kt ϵ Fl - вход функции выхода f в такте t и (zt) – ключевой поток. Функция FZ : Fr · l → F при Z ϵ Fr называется Z-функцией, когда при zt,…, zt+r-1 = Z, FZравно нулю на соответствующих входах Kt,…, Kt+r-1. То есть
(zt,…, zt+r-1) = Z => FZ (Kt,…, Kt+r-1) = 0 [3].
Если злоумышленник знает значения zt1,…,zt1+r-1,zt2,…,zt2+r-1,…,ztN,…,ztN+r-1, то используя перечисленные данные, он может составить следующую систему уравнений из Z-функций [2]:

Каждое Kt и Qt можно выразить через К и Q0, в результате, получаем, систему с неизвестными, обозначающими биты в S0, решая которое, можно определитьS0, то есть найти ключ ключевого потока.
Далее приведем определения и теоремы из [1], необходимые для нахождения решений системы уравнений (1); k[x1,…,xn] – множество всех полиномов от переменных x1,…, xn с коэффициентами над полем kс операциями сложения и умножения полиномов. Подмножество I множества k[x1,…,xn] называется идеалом, если выполнены следующие условия:
1. 0 ϵ I;
2. еслиf, g ϵ I, тоf + g ϵ I;
3. еслиf ϵ Iиh ϵ k[x1,…,xn], тоh∙f ϵ I.
Идеал, порожденный функциями f и g,обозначается через <f, g>.
Обозначим моном через ![]() , где α = (α1, … , αn) ϵ Zn≥0-n-векторы показателей степеней.Так каксуществует взаимно однозначное соответствие между мономами
, где α = (α1, … , αn) ϵ Zn≥0-n-векторы показателей степеней.Так каксуществует взаимно однозначное соответствие между мономами ![]() и n-наборами показателей степеней α = (α1, … , αn) ϵ Zn≥0, то упорядочение, которое мы определим на Zn≥0, определит и упорядочение на множестве мономов: если α>βв Zn≥0, то будем говорить, что χα > χβ. Определим градуированное обратное лексикографическое упорядочение на Zn≥0, пусть α, β ϵ Zn≥0, тогда говорим, что α>β, если
и n-наборами показателей степеней α = (α1, … , αn) ϵ Zn≥0, то упорядочение, которое мы определим на Zn≥0, определит и упорядочение на множестве мономов: если α>βв Zn≥0, то будем говорить, что χα > χβ. Определим градуированное обратное лексикографическое упорядочение на Zn≥0, пусть α, β ϵ Zn≥0, тогда говорим, что α>β, если

или |α|=|β| и самая правая ненулевая координата вектора α-β ϵ Zn≥0отрицательна.
Упорядочение мономов называется линейным, если для любой пары мономовχα и χβ выполняется ровно одно из следующих соотношений: χα > χβ, χα = χβ, χα < χβ.
При умножении монома на полином может нарушиться порядок членов, вследствие этого могут возникнуть трудности в алгоритме деления в k[x], так как произведение старшего члена полинома на моном может не быть старшим членом произведения. Поэтому требуется, чтобы упорядочение мономов обладало следующим дополнительным свойством: если χα > χβ, а χγ – произвольный моном, то χα χγ> χβχγ . В терминах векторов показателей степеней, это означает, что если α > β в Zn≥0 , то для любого γ ϵ Zn≥0 α + γ>β+γ.
Мономиальным упорядочением на k[x1,…,xn] называется любое бинарное отношение > на Zn≥0, обладающее следующими свойствами:
- > - линейное упорядочение на Zn≥0;
- если α > β и γ ϵ Zn≥0 , то α + γ > β+γ;
- > вполне упорядочивает Zn≥0, т.е. любое непустое подмножество в Zn≥0 имеет минимальный элемент по отношению к >.
![]() – ненулевой полином в k[x1,…,xn], и > мономиальное упорядочение, ɑα ϵ k:
– ненулевой полином в k[x1,…,xn], и > мономиальное упорядочение, ɑα ϵ k:
![]()
![]()
где максимум берется по отношению к >;
![]()
Пусть задано мономиальное упорядочение;конечное подмножество G = {g1,…,gs} элементов идеала Iназывается базисом Гребнера идеала, если<LT(g1),…, LT(gs)> = <LT(I)>.
{g1,…,gs}тогда и только тогда является базисом Гребнера идеала I, если старший член любого элемента из I делится на хотя бы один из LT(g1),…, LT(gs).
Редуцированным базисом Гребнера полиномиального идеала называется его базис Гребнера G, такой, что
- LC(p)=1 для всех p ϵ G;
- никакой моном никакого p ϵ G не принадлежит <LT(G-{p})>.
Пусть дана система уравнений над полем Fq:

Теорема[5].
Пусть дан идеал, составленный из уравнений над полем Fq из системы (2):
I = < f1,…,fn, x1q – x1, x2q – x2,…, xnq – xn >.
Для любого упорядочения редуцированный базис Гребнера имеет вид:
- {x1 – χ 1, x2 – χ2,…, xn – χn}, где (χ 1, χ2,…, χn) – решение системы уравнений (2)
- {1}, если система (2) не имеет решений.
Таким образом, найдя редуцированный базис Гребнера системы (1), составленной из Z - функций, находим её решение, т.е. ключ ключевого потока (начальное состояние (l,m)-комбайнера). При декодировании, зная ключ ключевого потока и соотношения для формирования ключевого потока, генерируем ключевой поток, выполняем операцию XOR над шифротекстом и ключевым потоком и определяем исходное информационное сообщение.
Разработанное программное средство базируется на С++, формирует систему алгебраических уравнений. Для нахождения редуцированного базиса Гребнера в данной работе использована программа Reduce, пакет BiBas программы Reduce вычисляет редуцированный базис Гребнера идеала из многочленов в поле F2 [4].
В таблице 1 приведены максимальные значения параметров l, m (l,m)-комбайнера, при которых возможно провести анализ поточного шифра с помощью созданной программы и программы Reduce. Анализ проводился при известных значениях первых нескольких бит ключевого генератора, соотношениях для формирования РСЛОС, функциях выхода и изменения состояния памяти (l,m)-комбайнера (в поле F2).
Таблица 1 – Результаты исследования
Параметры l,m (l,m) –комбайнера | Результат нахождения значений элементов S0 |
(2,1) | 1 |
(2,2) | 1 |
(2,3) | 1 |
(2,5) | 1 |
(2,11) | 1 |
(2,12) | 0 |
(3,0) | 1 |
(3,1) | 1 |
(3,5) | 1 |
(3,7) | 1 |
(3,8) | 0 |
(4,3) | 1 |
(4,4) | 0 |
(5,0) | i+p+s+1 = 0, o+a+d+1 = 0 остальные элементы найдены точно |
(5,1) | 0 |
(7,0) | y+i+p+s+f = 0,u+o+a+d+g = 0. остальные элементы найдены точно |
(8,0) | 0 |
Значение «1» в столбце «Результат нахождения значений элементов S0» таблицы 1 означает, что найдены все элементы в S0, значение 0 – не найден ни один элемент в S0.
Таким образом, с помощью разработанной программы и программы Reduce найдено первоначальное состояние (l,m)-комбайнера (ключ для построения ключевого потока поточного шифра). В результате проведения ряда программных экспериментов по анализу ключевого потока поточного шифра установлено, что наибольшие значения параметров l, m (l,m)-комбайнера, при которых можно найти программными способами (а именно с помощью разработанной программы на языке C++ и программы Reduce) его начальное состояние S0 при известных значениях первых нескольких бит ключевого генератора в поле F2, соотношениях для формирования РСЛОС, функциях выхода и изменения состояния памяти (l,m)-комбайнера (в поле F2) равны:
l=2, m=11,
l=3, m=7,
l=4, m=3,
при l=5,m=0 и при при l=7,m=0 можно сделать вывод о некоторых элементах S0.
При бὸльших параметрах, чем указанные выше, анализ поточных шифров при вышеперечисленных известных данных с помощью системы алгебраических уравнений неэффективен.
1. Кокс Д., Литл Дж., O’Ши Д. Идеалы, многообразия и алгоритмы. Введение в вычислительные аспекты алгебраической геометрии и коммутативной алгебры : пер. с англ. М.: Мир, 2000. 687 с.
2. Armknecht F. Algebraic attacks on certain stream ciphers: Inauguraldissertation zur Erlangung des akademischen Grades eines Doktors der Naturwissenschaften / Universitat Mannheim. Mannheim, 2006.
3. Courtois N. Algebraic attacks on combiners with memory and several outputs. Korea: ICISC, 2004.
4. DocumentationReduce. Режим доступа: http://www.reduce-algebra.com/packages.htm (дата обращения 20.01.2013).
5. Shannon C. Communication theory of secrecy systems // Bell Systems Techn. Journal. 1949. Vol. 28, № 4. pp. 656-719.
6. Stinson D. Cryptography. Theory and Practice. USA: CRC Press, Inc., 1995. 434 p.
Публикации с ключевыми словами: ключ, поточный шифр, базис Гребнера, регистр сдвига с линейной обратной связью
Публикации со словами: ключ, поточный шифр, базис Гребнера, регистр сдвига с линейной обратной связью
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



