научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#9 сентябрь 2005
В. 3. Кокотов, канд. техн. наук, НИИ "Аргон"
Алгоритм плотного размещения разногабаритных элементов на плате
Описывается алгоритм размещения разногабаритных элементов на плате. Автоматическое размещение высокой плотности достигается дихотомическим делением и плотной упаковкой. Предложен алгоритм быстрой плотной упаковки.
Характерной особенностью печатных узлов (ПУ) и типовых элементов замены (ТЭЗ) является установка на них разногабаритных электрорадиоэлементов (ЭРЭ).
Высокие коммутационные возможности современного печатного монтажа позволяют очень плотно устанавливать ЭРЭ на печатных платах. Однако большинство САПР весьма посредственно решают задачу плотного размещения разногабаритных ЭРЭ автоматическими методами, предлагая пользователю интерактивные режимы. При этом, несмотря на все возможные "облегчающие" средства графических редакторов, плотное размещение при достаточно большом числе ЭРЭ остается весьма трудоемкой задачей, занимающей значительную часть всего цикла конструкторского проектирования ПУ и ТЭЗ.
Ниже предлагается эффективный алгоритм для автоматического плотного размещения разногабаритных ЭРЭ, устанавливаемых без пересечения их проекций на одной стороне печатной платы, причем рассматривается случай, когда в качестве модели ЭРЭ используется минимальный прямоугольник, описывающий его проекцию на плату, и повороты таких прямоугольников недопустимы.
Постановка задачи плотного размещения разногабаритных ЭРЭ. Плотность размещения (q) ЭРЭ на плате можно характеризовать процентным отношением суммарной площади минимальных прямоугольников, описывающих проекцию ЭРЭ на плату (SЭРЭ), к площади поля размещения (Sпр)
Все ПУ и ТЭЗ по значениям q можно разбить на три следующих класса:
· неплотное размещение (q < 60 %);
· плотное размещение (60 % < q < 80 %);
· сверхплотное размещение (q > 80 %).
Для ПУ и ТЭЗ с разногабаритными ЭРЭ, имеющими q < 60 %, достаточно эффективны методы размещения равногабаритных ЭРЭ с небольшой модификацией, заключающейся в присвоении максимального габаритного размера всем ЭРЭ.
Для ПУ и ТЭЗ с разногабаритными ЭРЭ, имеющими q > 80 %, задача размещения практически сводится к задаче раскроя с возможными перестановками внутри групп равногабаритных ЭРЭ, поскольку для таких конструкций обычно число вариантов "раскроев" весьма ограничено. Для этих конструкций обычно эффективным методом является перебор всех возможных размещений.
Наибольшую сложность представляют конструкции с плотным размещением ЭРЭ (60 % < q < 80 %). Для этой группы методы расстановки равногабаритных ЭРЭ неприемлемы, так как в случае сведения габаритных размеров всех ЭРЭ к максимальному становится невозможным расположение их на поле размещения. Использовать же методы размещения с q > 80 % практически невозможно, так как полный перебор вариантов размещения ЭРЭ весьма велик. Поэтому плотное размещение разногабаритных ЭРЭ алгоритмически значительно сложнее неплотного и сверхплотного размещений.
В общем виде решение задачи плотного размещения разногабаритных ЭРЭ весьма сложно. Для упрощения решения приняты следующие ограничения:
· поле размещения представляется прямоугольником с габаритами, кратными дискретам сеточной модели поля трассировки;
· все ЭРЭ имеют прямоугольную форму с габаритами, кратными дискретам сеточной модели поля трассировки;
· все запрещенные для размещения ЭРЭ зоны внутри поля размещения представляются прямоугольниками с габаритами, кратными дискретам сеточной модели поля трассировки.
Такие ограничения уменьшают реальную плотность размещения ЭРЭ непрямоугольной формы. Однако это уменьшение даже для худших случаев не превышает 8 %.
Пусть каждый из прямоугольников ЭРЭ представлен множеством Pt точек пересечения дискрет сеточной модели поля трассировки, входящих в контур данного прямоугольника. Тогда при указанных ограничениях задача размещения разногабаритных ЭРЭ имеет следующую формальную постановку.
В прямоугольнике P0 с установленными внутри него прямоугольниками Pzk (запретами размещения) необходимо разместить по некоторому критерию F конечное множество разногабаритных прямоугольников Р = {Pi}, i = 1, 2,... n, имеющих связи между собой при выполнении следующих ограничений:
![]() для,
i ≠j где
для,
i ≠j где ![]() (1)
(1)
![]() для
для
![]() ;
(2)
;
(2)
![]() для
для
![]() ,
, ![]() (3)
(3)
ti ≤ tiдоп
для ![]() ,
(4)
,
(4)
где ti — значение конструктивно-технологического или другого параметра каждого ЭРЭ при полученном размещении; tiдоп — максимальное допустимое значение ti.
Выражение (1) — условие взаимного непересечения прямоугольников друг с другом.
Выражение (2) — условие размещения прямоугольников {Pi} в пределах прямоугольника Р0.
Выражение (3) — условие непересечения прямоугольников Pi с прямоугольниками Pzk, моделирующими запрещенные для размещения ЭРЭ зоны.
Выражение (4) — условие, требующее выполнения конструктивно-технологических или других ограничений для каждого размещаемого ЭРЭ.
Критерии и алгоритм плотного размещения разногабаритных ЭРЭ. Эффективность решения задачи размещения во многом определяется критериями, по которым осуществляется размещение.
Основным (прямым) критерием размещения ЭРЭ обычно является обеспечение стопроцентной трассировки. Однако, в силу сложности применения этого критерия на практике, используются косвенные критерии, которые имеют значительную корреляцию с прямым критерием. К таким критериям относятся [1, 2]:
· минимум суммарной взвешенной длины соединений;
· минимальное число соединений, длина которых больше заданной;
· минимальное число пересечений проводников;
· максимальное число соединений между элементами, находящимися в соседних позициях, либо в позициях, указанных разработчиком;
· максимальное число цепей простой конфигурации;
· равномерное распределение связей по монтажному пространству и т. д.
Иногда при размещении используются ограничения, не связанные с критерием стопроцентной трассировки. Такими ограничениями могут быть:
· ограничения в установке ЭРЭ, связанные с конструктивными особенностями платы (расположение крупногабаритных ЭРЭ в определенных зонах поля размещения);
· ограничения по тепловым характеристикам ЭРЭ (равномерность тепловыделения со всего поля размещения, ограничения на взаимное расположение ЭРЭ, выделяющих большое количество теплоты, и ЭРЭ, критичных к температурному режиму);
· ограничения по электромагнитной совместимости ЭРЭ (определенная удаленность ЭРЭ, излучающих сильные электромагнитные поля от ЭРЭ, критичных к электромагнитным полям).
Следует отметить, что использование таких ограничений ухудшает степень оптимальности получаемых решений по основному критерию — обеспечению стопроцентной трассировки.
Отличительной особенностью задачи плотного размещения разногабаритных ЭРЭ (60 % < q < 80 %) является то, что кроме прямого критерия (критерия трассируемости) должно выполняться условие размещения всех ЭРЭ в поле размещения. Поэтому доминирующим фактором при плотном размещении будет являться возможность такого размещения. Однако неучет прямого критерия может привести к плохой трассируемости. Таким образом, при плотном размещении доминирующим критерием принимается возможность размещения разногабаритных ЭРЭ на поле размещения, а вторым по важности критерием — прямой критерий размещения (критерий трассируемости). Однако, как указывалось выше, прямой критерий размещения не может быть использован в связи с ограниченностью машинных ресурсов. Поэтому вместо него используется какой-либо косвенный критерий трассируемости. В качестве такого критерия принят критерий минимального числа связей в сечениях [3]. Выбор этого критерия, с одной стороны, отвечает требованиям трассируемости, а с другой стороны, имеет известную конструктивную реализацию — дихотомическое деление (половинное деление) [1].
В рассматриваемом алгоритме доминирующим критерием является критерий возможности размещения разногабаритных ЭРЭ в подобластях поля размещения на каждом этапе дихотомического деления, которое обеспечивает размещение по косвенному критерию трассируемости при выполненном доминирующем критерии.
Данные два критерия являются противоречивыми. Действительно, возможна ситуация, когда размещенные на плате ЭРЭ "плохо трассируются", в то время как "хорошо трассируемое размещение" может не позволить установить на поле размещения все разногабаритные ЭРЭ. Такое противоречие характерно для существенно разногабаритных ЭРЭ (большая номенклатура некратногабаритных ЭРЭ).
Одним из способов совмещения используемых двух критериев является чередующееся их использование с приоритетом выбора вариантов по доминирующему критерию. В рассматриваемом алгоритме этот способ реализован в следующем виде.
На каждом этапе дихотомического деления (реализующего критерий трассируемости) проверяется выполнение доминирующего критерия (возможность размещения путем плотной упаковки ЭРЭ). Причем такие "упаковки" выбираются из нескольких вариантов, что позволяет результатом каждого шага дихотомического деления иметь вариант, удовлетворяющий доминирующему критерию. Более того, выбор такого результата из нескольких вариантов позволяет создать предпосылки для получения положительных результатов дихотомического деления на следующих итерациях.
Изложенный подход предполагает априорную конструктивную возможность "упаковки" всех ЭРЭ на поле размещения платы. При этом возможны две стратегии:
· перед началом работы алгоритма проводится "ручная" упаковка всех ЭРЭ на плате без учета из связности;
· автоматическая упаковка всех ЭРЭ на плате без учета их связности алгоритмом плотной упаковки.
Отрицательный результат при использовании любой из этих стратегий свидетельствует о невозможности применения предлагаемого алгоритма для конкретного объекта проектирования.
Размещение по критерию минимального числа связей в сечениях. Для минимизации числа связей в сечениях используется алгоритм дихотомического деления. Суть алгоритма дихотомического деления заключается в иерархическом разделении текущего множества ЭРЭ на два подмножества (A и B), равные по числу ЭРЭ (с точностью до одного ЭРЭ) и имеющие между собой минимум связей. Полное решение задачи дихотомического деления может быть получено только путем полного перебора вариантов. Поэтому используется эвристический подход. Одним из наиболее эффективных подходов (по использованию машинных ресурсов) является способ последовательных чередующихся перемещений ЭРЭ из одного подмножества в другое. При этом существенным является выбор критерия для определения ЭРЭ, переносимого из одного множества в другое. От выбора этого критерия существенно зависит не только конечный результат и число циклов переноса, но и сходимость алгоритма.
Ясно, что доминирующим фактором в таком критерии должна быть степень связности данного ЭРЭ с ЭРЭ подмножеств A и B. Однако, по соображениям электронного конструирования, в этих критериях часто учитывается и такой фактор, как минимум длины будущих связей между ЭРЭ, а также всевозможные факторы, прямо или косвенно учитывающие специфику конструкции объекта проектирования и ЭРЭ.
В [4] рассмотрен алгоритм дихотомического деления, в котором в качестве критерия для выбора переносимого ЭРЭ используется критерий, учитывающий как связность ЭРЭ с ЭРЭ подмножеств A и B, так и ограничения на длину предполагаемых связей, а кроме того, степень совместимости разногабаритных ЭРЭ в текущей области деления. Однако учет в критерии выбора переносимого ЭРЭ любого фактора, кроме доминирующего, ухудшает "качество" выбора переносимого ЭРЭ по доминирующему фактору. Поэтому в таком критерии (помимо доминирующего фактора) учитывается только фактор превышения заданной максимальной длины связи. Более того, степень учета фактора превышения максимальной длины задается управляющим параметром программной реализации, что позволяет оперативно настраиваться на значимость этого фактора в критерии.
С учетом изложенного и выражения критерия, данного в [4], предлагается в качестве критерия выбора переносимого ЭРЭ использовать
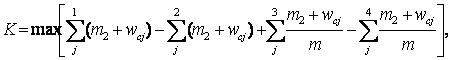 (5)
(5)
где m2 — вес связи в одной цепи; wcj — вес штрафа за превышение длины в j-й цепи; m — максимальное число контактов одного ЭРЭ.
Причем суммирование проводится только по тем цепям, в которых присутствует данный ЭРЭ. Правила суммирования следующие:
·
![]() — данный ЭРЭ в j-й цепи — единственный из "своего"
подмножества A(A),
и в этой же цепи присутствуют ЭРЭ "чужого" подмножества B(A);
— данный ЭРЭ в j-й цепи — единственный из "своего"
подмножества A(A),
и в этой же цепи присутствуют ЭРЭ "чужого" подмножества B(A);
·
![]() — в j-й
цепи присутствуют другие ЭРЭ из того же подмножества А(В),
которому принадлежит данный ЭРЭ, и отсутствуют ЭРЭ из "чужого"
подмножества В(А);
— в j-й
цепи присутствуют другие ЭРЭ из того же подмножества А(В),
которому принадлежит данный ЭРЭ, и отсутствуют ЭРЭ из "чужого"
подмножества В(А);
·
![]() — в j-й
цепи присутствует более одного ЭРЭ из того же подмножества А(В),
которому принадлежит данный ЭРЭ, а число ЭРЭ из "чужого" подмножества
В(А) в данной цепи больше или равно числу ЭРЭ из
"своего" подмножества А(В);
— в j-й
цепи присутствует более одного ЭРЭ из того же подмножества А(В),
которому принадлежит данный ЭРЭ, а число ЭРЭ из "чужого" подмножества
В(А) в данной цепи больше или равно числу ЭРЭ из
"своего" подмножества А(В);
·
![]() — в j-й
цепи присутствует более одного ЭРЭ из того же подмножества А(В),
которому принадлежит данный ЭРЭ, а число ЭРЭ из "чужого" подмножества
В(А) в данной цепи меньше, чем число ЭРЭ из "своего"
подмножества А(В) без единицы.
— в j-й
цепи присутствует более одного ЭРЭ из того же подмножества А(В),
которому принадлежит данный ЭРЭ, а число ЭРЭ из "чужого" подмножества
В(А) в данной цепи меньше, чем число ЭРЭ из "своего"
подмножества А(В) без единицы.
Такой критерий обеспечивает с высшим приоритетом выбор ЭРЭ, перенос которого из подмножества А(В) в подмножество В(А) максимально уменьшает число связей между подмножествами A и B, а при отсутствии таких ЭРЭ — выбор ЭРЭ, способствующего при дальнейших переносах уменьшить число этих связей. Кроме того, выбор таких правил суммирования обеспечивает сходимость процесса переносов при значениях K> 0. Таким образом, при значениях K ≤ 0 процесс следует закончить.
Следует отметить, что экспериментальная проверка этого критерия показала возможность на некоторых итерациях увеличить число связей между ЭРЭ подмножеств А и В, но общая тенденция к уменьшению числа таких связей наблюдалась во всех проведенных экспериментах. Однако указанные увеличения числа связей иногда наблюдались и на последних итерациях. Поэтому в процессе перемещения ЭРЭ предусмотрена фиксация варианта подмножеств А и В с минимальным (по всем итерациям) числом таких связей для окончательного принятия именно этого варианта.
Величина штрафа wcj в (5) вычисляется, как

где max(pj) — максимальная оценка полупериметра описывающего прямоугольника j-й цепи; min(pj) — минимальная оценка полупериметра описывающего прямоугольника j-й цепи; md — порог штрафуемой длины связи; m1 — максимальный штраф за превышение допустимой длины связи.
Величины m1, m2 и md являются управляющими параметрами программной реализации и их значения могут задаваться перед началом работы. В алгоритме плотного размещения разногабаритных ЭРЭ весьма существенным является способ установки границы между подобластями расположения подмножества ЭРЭ A и B. Представляется эффективным при каждом делении области устанавливать границу на середине между границами минимальных раскроев (или "упаковок") в каждой из подобластей A и B. Такой подход, хотя и не учитывает потребности в площади для следующих итераций, однако не "ущемляет" в площади ни одно из подмножеств A и B.
Кроме того, эффективным является альтернативный выбор из
"горизонтального и вертикального разрезания" области. Критерием
такого альтернативного выбора принят максимум зазора между плотными
"упаковками" в подобластях подмножеств ЭРЭ А и В с
учетом дефицита трасс соответствующего направления. Так, при ![]() (dx — зазор по оси X между
плотными "упаковками"; dy — зазор
по
оси Y между плотными
"упаковками"; h — высота области;
w — ширина области) выбирается "вертикальное
разрезание", а в противном случае — "горизонтальное".
(dx — зазор по оси X между
плотными "упаковками"; dy — зазор
по
оси Y между плотными
"упаковками"; h — высота области;
w — ширина области) выбирается "вертикальное
разрезание", а в противном случае — "горизонтальное".
Существенным также является альтернативный выбор установки ЭРЭ подмножества A в верхнюю или нижнюю (в правую или левую) подобласть дихотомического деления и соответственно ЭРЭ множества B — в нижнюю или верхнюю (в левую или правую) подобласть дихотомического деления. Такой альтернативный выбор целесообразно вести, учитывая число связей ЭРЭ подмножества A и ЭРЭ подмножества B с ЭРЭ, расположенными ниже (выше) области размещения ЭРЭ множества A и B.
При изложенном подходе может оказаться, что при выбранном разделении ЭРЭ на подмножества A и B область поля размещения ЭРЭ множества A и B не может быть разделена одной вертикальной (горизонтальной) границей на две подобласти, в которых помещались бы ЭРЭ соответственно подмножеств A и B. В этом случае в данной области размещаются ЭРЭ множества А и В и между ними устанавливаются по возможности максимальные зазоры (уменьшение концентрации монтажных точек, что является существенным фактором для будущей трассировки).
"Быстрая" плотная упаковка. В алгоритме плотного размещения ЭРЭ многократно проводится плотная упаковка ЭРЭ. Задача такой упаковки является частным случаем задачи раскроя, которая в этом случае имеет следующие особенности:
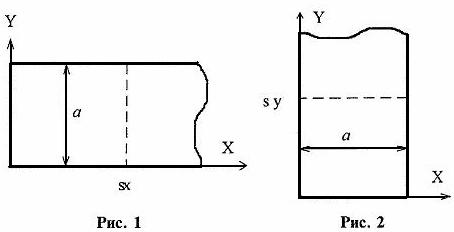
· раскрой проводится на полубесконечной ленте (горизонтальной или вертикальной). Материал раскроя есть полубесконечная лента заданной ширины а (горизонтальная лента — рис. 1 или вертикальная лента — рис. 2). Требуется так разместить ЭРЭ, чтобы длина sx (sy) участка полосы, заключающего размещаемые ЭРЭ, была минимальной;
· ЭРЭ, укладываемые на участке ленты, — ориентированные прямоугольники;
· укладка ЭРЭ осуществляется без зазоров;
· критерий оптимизации — минимальная длина участка ленты размещения sx (sy);
· результаты решения — величина sx (sy) и координаты расположения всех ЭРЭ.
В [5] рассмотрен метод последовательно-одиночного размещения, при котором последовательности размещаемых ЭРЭ генерировались заранее. Такой подход требует значительного машинного времени, поскольку число последовательностей при этом весьма велико даже для небольшого числа ЭРЭ.
Для сокращения машинного времени предлагается вести последовательную установку не по заранее определенной последовательности, а формировать такую последовательность в процессе последовательной установки, пользуясь определенными критериями на каждом шаге установки. Такой подход позволяет проводить размещение всего по одной последовательности, однако "расплатой" за это является возможное не оптимальное, а рациональное решение задачи раскроя. Это происходит потому, что на каждом шаге установки (после установки каждого ЭРЭ) проводится локальный (для данного шага) поиск следующего ЭРЭ последовательности для установки. Таким образом, на каждом шаге установки выполняется локально-оптимальный выбор члена последовательности и локально-оптимальная его установка.
Далее задача раскроя будет рассматриваться для горизонтальной полубесконечной ленты.
При установке очередного ЭРЭ выбирается такой ЭРЭ (если таковой существует), установка которого не увеличивала бы площадь установки, ограниченной sx на текущем шаге. Если таких ЭРЭ окажется несколько, то из них выбирается ЭРЭ с наибольшей площадью. Это, во-первых, позволит более плотно занять участок размещения, ограниченный sx, а, во-вторых, создает предпосылку меньшего увеличения площади раскроя на следующих шагах. При отсутствии таких ЭРЭ на очередном шаге установки выбирается ЭРЭ, занимающий максимальную площадь в участке размещения, ограниченном текущим sx (это позволит максимально занять площадь, ограниченную текущим sx). Если таких ЭРЭ несколько, то из них выбирается ЭРЭ, имеющий максимальную площадь. В результате для последующих шагов установки остаются ЭРЭ с меньшей площадью, что является предпосылкой для меньшего увеличения значения sx.
Особый критерий используется при выборе первого ЭРЭ для установки. Здесь выбирается ЭРЭ, имеющий максимальный размер по оси X. Это позволяет на последующих шагах избежать (уменьшить вероятность) установки такого ЭРЭ, который может сильно увеличить границу области размещения. Кроме того, это создает предпосылку для установки других ЭРЭ (с меньшим размером по оси X) на ближайших первых шагах без увеличения границы sx площади раскроя.
Таким образом, общий подход при выборе очередного (k-го) ЭРЭ для установки может быть сформулирован следующим алгоритмом.
Имеется k — 1 размещенных ЭРЭ и величина
sxk-1 — текущее sx и ЭРЭ с габаритными размерами ![]() , который следует
разместить (рис. 3).
, который следует
разместить (рис. 3).
При k = 0 выбирается ЭРЭ с максимальной шириной. Если среди неразмещенных ЭРЭ есть такие, что их установка не приводит к увеличению sx (sxk = sxk-1), то среди них выбирается такой, у которого площадь максимальна. Иначе:
·
выбираются такие ЭРЭ, которые в прямоугольнике ![]() занимают
максимальную площадь;
занимают
максимальную площадь;
·
если ЭРЭ, занимающих максимальную площадь в ![]() (одну и ту же),
несколько, то выбирается ЭРЭ, имеющий максимальную площадь.
(одну и ту же),
несколько, то выбирается ЭРЭ, имеющий максимальную площадь.
Выбранный для установки ЭРЭ размещается на такое место, чтобы его правая граница была минимально удалена от начала полубесконечной ленты. Это обеспечит минимально возможное отсутствие "пустот" в левой части полубесконечной ленты, что, в свою очередь, дает предпосылки к более плотному заполнению ленты, а следовательно, к получению меньшего конечного значения
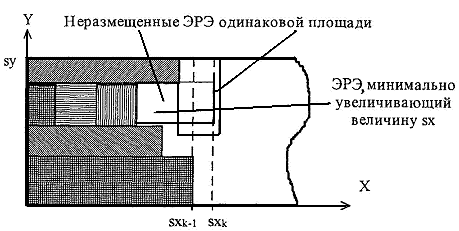
Рис.3
При наличии нескольких таких мест среди них выбирается такое, при котором длина границы соприкосновения устанавливаемого ЭРЭ с уже установленными ЭРЭ и границей полубесконечной ленты была бы максимальной. Это создает предпосылку для установки следующих ЭРЭ (на следующих шагах) на одном уровне по координате X с данным устанавливаемым ЭРЭ. Тогда алгоритм размещения очередного члена последовательности может быть сформулирован следующим образом.
Имеется k — 1 размещенных ЭРЭ, величина sxk-1 — текущее sx и размещаемый ЭРЭ (рис. 4).
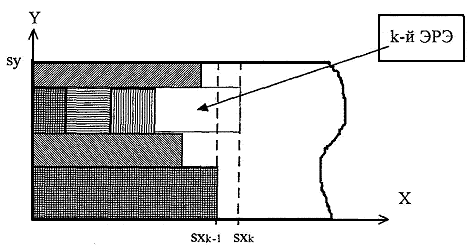
Рис. 4.
Для установки к-то ЭРЭ находится такое место размещения, чтобы правая граница данного ЭРЭ создавала минимальное значение sxk. Если таких мест несколько, то выбирается то из них, на котором данный ЭРЭ имел бы максимальное по протяженности соприкосновение с уже установленными ЭРЭ или границей ленты размещения.
Описанный алгоритм плотного размещения ЭРЭ программно реализован в САПР RELEF [6]. Использование данной программной реализации для размещения ЭРЭ на реальных объектах проектирования показало высокую эффективность предложенного алгоритма при 60 % < q < 80 %. Причем во многих случаях размещения, выполненные этим алгоритмом, давали лучшие результаты последующей трассировки, чем размещения, выполненные "ручным" способом опытным конструктором.
Список литературы
1. Абрайтис Л. Б. Автоматизация проектирования топологии цифровых интегральных микросхем. М.: Радио и связь, 1985. 198 с.
2. Петренко А. И., Тетельбаум А. Я. Формальное конструирование электронно-вычислительной аппаратуры. М.: Сов. радио, 1979. 256 с.
3. Breuer M. Min — cut placement. — J. Des. Autom. and Fault - Tolerant Comput., 1997. V. 1. P. 343—362.
4. Tong Gao, Vaidya P. M., Liu С L. A performance driven macro-cell placement algorithm: 29th ACM/IEEE Design Automation Conference, 1992. P. 147—152.
5. Стоян Ю. Г. Размещение геометрических объектов. Киев: Наукова думка, 1975. 234 с.
6. Кокотов В. 3., Сычева Е. В. САПР рельефного монтажа. PCWEEK (RUSSIAN EDITION), 1998, 24 марта-30 апреля. № 11 (135). С. 37.
СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 11, 1998
Ключевые слова: Алгоритмы размещения, разногабаритные элементы, плотная упаковка, трассировка, минимизация связей, критерии эффективности.
Публикации с ключевыми словами: трассировка, Алгоритмы размещения, разногабаритные элементы, плотная упаковка, минимизация связей, критерии эффективности
Публикации со словами: трассировка, Алгоритмы размещения, разногабаритные элементы, плотная упаковка, минимизация связей, критерии эффективности
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



