научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#9 сентябрь 2005
М
М. М. Хрусталев, д-р физ-мат. наук проф.,
Б. И. Пустовит, гл. эксперт МО РФ,
В. Е. Зотов, канд. техн. наук доц., МАИ,
В. А. Дроздов, ИМАШ РАН
Принципы построения системы математических моделей отрасли (комплекса)
Статья посвящена проблеме построения системы математических моделей, описывающих функционирование отрасли (комплекса) на всех этапах жизненного цикла. Введены принципиальные понятия — суммарная масса объектов и масса разнообразия, позволяющие сформировать базовую математическую модель. На ее основе строятся все составляющие модели облика отрасли. Приведены основные уравнения и ограничения для описания процессов создания объектов, накопления их с учетом возраста, динамики основных фондов и затрат, оценки качества.
Введение
Проблема развития страны подразумевает комплексный подход к выработке и реализации решений в политике, экономике, обороне, науке, технике, образовании и других сферах деятельности граждан. Одной из задач является создание и обеспечение функционирования отраслей народного хозяйства, оборонного комплекса и других государственных структур, которые подставляют собой сложные многосвязные иерархические системы. Авторы придерживались системного подхода к объекту исследования как к комплексу технических систем, средств и персонала, который ими управляет и обслуживает. Основная концепция, принятая при построении системы математических моделей, — это баланс между разработкой, производством технических систем и средств (ТТС) и их эксплуатацией.
Методологические вопросы анализа больших систем, проблемы их формализации и моделирования рассматривались во многих работах [1—5]. Существенные результаты получены в теории сложных иерархических систем [6—9]. Имеются работы по формированию математических моделей экономики [10—14]. Однако унифицированный подход к построению комплексной системы моделей функционирования отрасли практически не разработан. Для описания любой системы необходимо рассмотреть все этапы ее жизненного цикла, начиная от создания и кончая списанием и утилизацией. Описывать динамику развития и существования предлагается с применением уравнений, используемых при изучении динамики биологических популяций [16]. На рис. 1 показан состав отрасли как части экономики страны и обратная связь с идеологической надстройкой, на базе которой и формируется ее содержание. Понятно, что в основе построения отрасли должна лежать концепция "стоимость—эффективность". Необходимо реализовать принятую концепцию построения с минимальными экономическими затратами. На приведенной схеме выделены основные функциональные блоки, которые представлены разработанными формальными математическими моделями. Описать же концепцию построения можно лишь на языке представления знаний, что является отдельной задачей, развитием проводимых исследований.
В предложенной системе моделей отражены следующие составляющие разработки технических систем и средств, подготовки персонала (управленческого, целевого, обслуживающего, вспомогательного), функционирования подразделений отрасли (рис. 2):
· фундаментальные научные исследования;
· прикладные научные исследования в области создания ТСС и смежных областях;
· проектирование и опытное производство новых видов ТСС;
· разработка технологий и серийное производство ТСС;
· функционирование подразделений, включая ТСС, персонал и основные фонды;
· обучение и переобучение персонала; потери и утилизация ТСС;
· уровень совершенства новых и серийных видов ТСС;
· качество и количественный состав подразделений отрасли.

Рис. 1. Отрасль (комплекс), облик и функциональные связи
Очевидно, что математические модели угледобывающей отрасли народного хозяйства по составу, содержанию и связям будут отличаться от подобных моделей, описывающих нефтедобывающую отрасль или оборонный комплекс. Специфика предметной области должна непосредственно учитываться на всех этапах построения системы математических моделей.
Разработанная система математических моделей представляет собой совокупность дифференциальных и интегральных уравнений различных типов и алгебраических соотношений между переменными. На основе имеющегося опыта [15] и семантического анализа проблемной области было выявлено, что математическое описание многих фрагментов отрасли может быть унифицировано. Была сформирована базовая модель создания группы динамических объектов (знаний, проектов, технологий, изделий), на основе которой с небольшой коррекцией построены все основные математические модели отрасли, описывающие ее функционирование на всех этапах жизненного цикла, начиная с разработки ТСС, эксплуатации и кончая списанием и утилизацией ТСС.

Рис. 2. Состав отрасли (комплекса)
Другая принципиальная идея, положенная в основу построения системы моделей, касается способа и единиц измерения объема продукта в различных сферах отрасли. Инфляция, надуманный курс рубля и прочие причины не позволяют в текущий момент использовать прежние стоимостные единицы. Если объем выпуска серийного производства можно измерять стоимостью выпускаемых в год изделий, то гораздо сложнее дело обстоит с объемом фундаментальных знаний, необходимых для создания образца ТСС, объемом продукта сфер проектирования, опытного производства, испытаний, доводки и т. д. Есть принципиальная разница между выпуском серийного производства и выпуском продукта КБ или НИИ. Серийное производство создает некоторую массу (количество) объектов, а КБ или НИИ создает разнообразие объектов (новые, спроектированные).
В связи с этим в системе предлагаемых моделей присутствуют две принципиально различные характеристики объема выпускаемого продукта: суммарная масса и масса разнообразия, характеризующая количество типов ТСС. За единицу измерения этих величин предлагается принять затраты на соответствующих этапах разработки (от проведения НИР до создания опытных образцов и законченных испытаний) какого-либо конкретного образца ТСС. Такой образец следует назвать эталонным. Для эталонного образца масса разнообразия на каждом этапе создания (фундаментальные исследования, прикладные исследования, проектирование и т. д.) принимается равной единице. Стоимость же создания единицы массы продукта на каждом из этапов совпадает с долей стоимости создания эталонного образца. Суммарная стоимость создания эталонного образца принимается за единицу. Для другого образца ТСС масса разнообразия равна отношению стоимости разработки этого образца ТСС к стоимости разработки эталонного образца.
В предлагаемой системе моделей фигурируют в основном потоки массы разнообразия и суммарной массы, т. е. массы создаваемой, передаваемой в единицу времени. Для краткости слово "поток" обычно опускается. Такой подход позволяет формировать простые агрегированные варианты системы моделей, где в том или ином смысле близкие виды ТСС объединяются и рассматриваются как один продукт, но с большей массой разнообразия.
Серийное производство каждого вида ТСС характеризуется двумя величинами: массой разнообразия и суммарной массой ТСС. Суммарная масса годового выпуска серийного производства определяется как отношение стоимости выпущенных ТСС к стоимости серийного экземпляра эталонного образца ТСС. Если выпускается только эталонный образец, масса совпадает с количеством. Стоимость серийного экземпляра как эталонного образца, так и других, измеряется в долях стоимости разработки эталонного образца.
На этапе эксплуатации ТСС также присутствуют две характеристики: масса разнообразия и суммарная масса. Такой прием позволяет даже на уровне простой монопродуктовой модели (один обобщенный вид ТСС) учесть затраты на создание необходимого разнообразия видов ТСС.
Из определения понятия массы разнообразия следует, что условием сбалансированного (устойчивого) функционирования отрасли является выполнение закона сохранения потока массы разнообразия. Поток массы разнообразия не может возрастать при переходе от этапа к этапу: НИР, проектирование, опытное производство, испытание, серийное производство. Нарушение этого условия ведет к обрыву производственной цепочки. Тем не менее на некоторых этапах в единицу времени может производиться меньшая масса разнообразия, чем требуется на последующем этапе. Баланс потока массы разнообразия достигается за счет использования ранее созданной массы. Например, если почти полностью прекратить разработку новых видов ТСС, серийное производство может по-прежнему работать, не снижая годового выпуска с использованием наработанной ранее массы разнообразия, но будет вынуждено все больше и больше увеличивать временной лаг использования старых технологий. Это приведет к моральному старению выпускаемых ТСС. Такие эффекты учитываются в приведенной ниже базовой модели, положенной в основу системы математических моделей отрасли.
Базовая модель создания группы динамических объектов
Для унификации описания большой системы, которой является отрасль народного хозяйства, предлагается следующая базовая концептуальная модель. Основные блоки модели (рис. 3) описывают процессы создания объектов, накопления готовых объектов с учетом возрастной структуры, динамику основных фондов и затрат как экономическую подсистему, оценку качества (современности и пригодности) созданных объектов. Под объектами понимаются не только физические изделия, но и знания — проекты, технологии, методики и т. д.
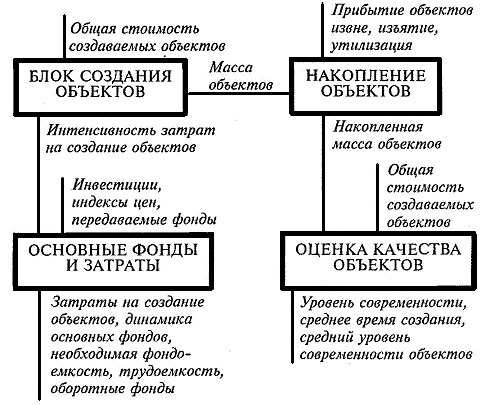
Рис. 3. Функциональная схема базовой модели создания динамических объектов
Создание объектов. Определим затраты и их интенсивность при создании объектов. Введем нормированную функцию затрат ![]() :
:

где ![]() — параметр интенсификации создания объекта; η — тип объекта.
— параметр интенсификации создания объекта; η — тип объекта.
Пусть T0(η) — время создания объекта типа η с нормальной интенсивностью работ ![]() — общая стоимость (масса) всех объектов типа η, создаваемых с интенсивностью λ, с момента начала создания
— общая стоимость (масса) всех объектов типа η, создаваемых с интенсивностью λ, с момента начала создания ![]() — коэффициент удорожания (удешевления) стоимости создания объектов типа η (если λ≠ 1);
— коэффициент удорожания (удешевления) стоимости создания объектов типа η (если λ≠ 1); ![]() — затраты в единицу времени на создание объекта типа η с интенсивностью λ; С0 (η) — доля стоимости объекта типа η, расходуемая на его создание в рамках данной модели.
— затраты в единицу времени на создание объекта типа η с интенсивностью λ; С0 (η) — доля стоимости объекта типа η, расходуемая на его создание в рамках данной модели.
Удельные затраты определяются через функцию затрат с учетом интенсивности работ соотношением

Здесь ![]() — время создания объекта типа η с интенсивностью λ. В момент t можно использовать следующую массу объектов типа η:
— время создания объекта типа η с интенсивностью λ. В момент t можно использовать следующую массу объектов типа η:

Интенсивность затрат на создание объектов типа η (затраты в единицу времени) в момент t определяются равенством
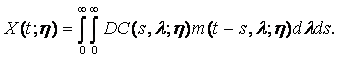
Все множество объектов по типу η разбито на группы ![]() в соответствии с подразделениями отрасли. В момент t можно использовать массу объектов из класса
в соответствии с подразделениями отрасли. В момент t можно использовать массу объектов из класса ![]() :
:

Интенсивность затрат (в базовых ценах) на создание объектов из группы ![]() в момент t определяется равенством
в момент t определяется равенством
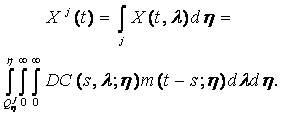
Накопление объектов. Готовые объекты накапливаются, стареют, их общая масса во времени изменяется по разным причинам. Обозначим M(t, λ; η) накопленную массу объектов типа η, имеющих возраст ![]() . Для описания накапливаемой во времени массы готовых объектов с учетом возраста используется следующее уравнение в частных производных (уравнение развития биологических популяций [16]):
. Для описания накапливаемой во времени массы готовых объектов с учетом возраста используется следующее уравнение в частных производных (уравнение развития биологических популяций [16]):

Здесь t — время, ![]() — возраст объекта;
— возраст объекта; ![]() — прибытие объектов возраста
— прибытие объектов возраста ![]() в момент t из "внешнего мира";
в момент t из "внешнего мира"; ![]() — изъятие объектов "во внешний мир";
— изъятие объектов "во внешний мир"; ![]() — гибель, или утилизация объектов (в долях от общей массы М), 0 ≤
— гибель, или утилизация объектов (в долях от общей массы М), 0 ≤ ![]() .
.
Граничные условия для этого уравнения имеют вид
![]()
Процесс накопления готовых объектов разных возрастов описывается интегральными уравнениями

где ![]() .
.
Граничные условия те же, что и раньше.
Модель основных фондов и затрат. Для описания процесса создания объектов, принадлежащих к конкретному классу ![]() , введем:
, введем:
· необходимую потребность в основных фондах ![]()
· необходимую потребность в трудовых ресурсах ![]() ;
;
· необходимую потребность в оборотных фондах ![]() .
.
Здесь ![]() — фондоемкость;
— фондоемкость; ![]() — трудоемкость;
— трудоемкость; ![]() — необходимость в оборотных фондах
— необходимость в оборотных фондах ![]() — коэффициент, отражающий влияние научно-технического прогресса.
— коэффициент, отражающий влияние научно-технического прогресса.
Динамика создания (разрушения) основных фондов описывается уравнением, хорошо известным из экономики:
![]()
где ![]() , ADK — коэффициенты использования инвестиций и фондов, пришедших со стороны; Vj(t) — инвестиции; DKj(t) — основные фонды, передаваемые из других отраслей (в другие отрасли);
, ADK — коэффициенты использования инвестиций и фондов, пришедших со стороны; Vj(t) — инвестиции; DKj(t) — основные фонды, передаваемые из других отраслей (в другие отрасли); ![]() — характерное время отдачи инвестиций;
— характерное время отдачи инвестиций; ![]() — характерное время переориентации основных фондов;
— характерное время переориентации основных фондов; ![]() — выбытие основных фондов вследствие их старения, разрушения и т. д.
— выбытие основных фондов вследствие их старения, разрушения и т. д.
Затраты в единицу времени на разработку (создание) объектов из класса ![]() с учетом инфляции определяются равенством
с учетом инфляции определяются равенством

где ![]() — индекс средней цены на разработку объекта класса
— индекс средней цены на разработку объекта класса ![]() ;
; ![]() — индекс цен на основные фонды;
— индекс цен на основные фонды; ![]() — индекс цен — отношение стоимости создания объектов типа η внутри страны к стоимости получения их извне;
— индекс цен — отношение стоимости создания объектов типа η внутри страны к стоимости получения их извне; ![]() — цена переориентации основных фондов на другую продукцию.
— цена переориентации основных фондов на другую продукцию.
Оценка современности объектов. Под современностью будем понимать среднюю интенсивность разработки новых объектов. Уровень современности объектов типа η, созданных в момент t, оценивается величиной

Среднее время разработки объектов типа η, законченных в момент t, определяется величиной ![]()
Уровень современности объектов типа η, созданных в момент ![]() , т. е. "пролежавших на складе" время, равное
, т. е. "пролежавших на складе" время, равное ![]() , определяется выражением
, определяется выражением
![]()
где ![]() - среднее время создания объекта.
- среднее время создания объекта.
Средний уровень современности накопленных к моменту ![]() объектов типа η определяется величиной
объектов типа η определяется величиной

где 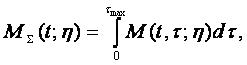 — суммарная масса объектов всех возрастов.
— суммарная масса объектов всех возрастов.
На основе предложенной базовой модели формируются все основные системы математических моделей, описывающие функционирование отрасли и ее облик.
Список литературы
1. Моисеев Н. Н. Человек, среда, общество. Проблемы формализованного описания. М.: Наука, 1982.
2. Моисеев Н. Н. Математические задачи системного анализа. М.: Наука, 1981.
3. Проблемы программно-целевого планирования и управления / Под ред. Г. С. Поспелова. М.: Наука, 1981.
4. Математическое моделирование: процессы в сложных экономических и экологических системах. М.: Наука, 1986.
5. Программно-целевой метод в планировании / Под ред. Н. П. Федоренко, М.: Наука, 1982.
6. Месарович М., Мако Д., Такахара И. Теория многоуровневых иерархических систем. М.: Мир, 1973.
7. Бурков В. Н. Большие системы: моделирование организационных механизмов. М.: Наука, 1989.
8. Снапелев Ю. М. Моделирование и управление в сложных системах. М.: Сов. радио, 1979.
9. Цвиркун А. Д. Основы синтеза структур сложных систем. М.: Наука, 1982.
10. Ашманов С. А. Введение в математическую экономику. М.: Наука, 1984.
11. Ланкастер К. Математическая экономика. М.: Сов. радио, 1972.
12. Дубровский С. В., Уздемир А. П. и др. Математические модели экономических процессов. М.: МЦНТИ, 1977.
13. Винн Р. Ф., Холден К. Введение в прикладной эконометрический анализ. М.: Фин. и статистика, 1981.
14. Иванов Ю. Р., Токарев В. В. Математическое описание элементов экономики. М.: Наука, 1994.
15. Матросов В. М., Хрусталев М. М. и др. Математическое моделирование экономических показателей эволюции транспортного комплекса России и проблема устойчивости развития // Транспорт: наука, техника, управление. М.: ВИНИТИ, 1995, № 1. С. 8-15.
16. Динамическая теория биологических популяций / Под ред. Р. А. Полуэктова. М.: Наука, 1974.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 10, 1998
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Ключевые слова: Системный анализ, иерархические системы, математическое моделирование, отраслевое планирование.
Публикации с ключевыми словами: математическое моделирование, иерархические системы, отраслевое планирование, системный анализ
Публикации со словами: математическое моделирование, иерархические системы, отраслевое планирование, системный анализ
Смотри также:
- Система моделей для исследования динамики развития и устойчивости функционирования отрасли
- 77-48211/638257 О преподавании учебной дисциплины “Математическое моделирование”
- Математическая модель перспективного испытательно-измерительного тренажерного стенда для освоения и оценки работоспособности специального оборудования быстроходных машин
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



