научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#9 сентябрь 2005
А. А. Харламов, канд. техн. наук, АОЗТ Научно-исследовательский центр "Нейроинформатика",
Г. Н. Рябов, Министерство науки и технологии РФ
Авторы выражают благодарность И. П. Муравьеву, который своими критическими оценками информационных характеристик сети помог выбрать оптимальный вариант архитектуры сети.
Использование сигмоидной функции в нейроподобных элементах с временной суммацией входных сигналов в составе динамической нейронной сети
Динамическая нейронная сеть (ДНС) на основе нейроподобных элементов (НЭ) с временной суммацией входных сигналов, в которых использовалась пороговая функция [1], обладает свойствами запоминания информационных последовательностей, их воспроизведения и ассоциативного обращения к информации, а также структурной многоуровневой ее обработки, в том числе, формирования поуровневых словарей и грамматик (восстановления структуры связей слов словарей во входной информации) и, наконец, фильтрации старой информации в потоке новой. Введение в НЭ сигмоидной функции вместо бинарной расширяет возможности ДНС по формированию более адекватного следа входной информации и, следовательно, позволяет более надежно и точно представлять эту информацию и более точно ее распознавать.
Введение
Существует класс ДНС на основе НЭ с временной суммацией входных сигналов, обладающих рядом интересных свойств с точки зрения обработки динамической информации. Особенностью этих сетей является использование НЭ, включающих в свой состав так называемого обобщенного дендрита — многоразрядного регистра сдвига (цепочки задержек с сумматорами). Если 2n таких НЭ объединить параллельно, причем каждый из них должен иметь один из полного набора адресов — так называемое динамическое ассоциативное запоминающее устройство (ДАЗУ), то эти НЭ осуществляют отображение F двоичной последовательности A в n-мерное сигнальное пространство Rn:
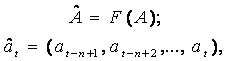
где ![]() —
траектория (последовательность точек
—
траектория (последовательность точек ![]() — вершин n-мерного
единичного гиперкуба). При этом любой фрагмент последовательности длины n найдет отклик в одном из НЭ. Существует обратное F преобразование F-1 траектории
— вершин n-мерного
единичного гиперкуба). При этом любой фрагмент последовательности длины n найдет отклик в одном из НЭ. Существует обратное F преобразование F-1 траектории ![]() в исходную
последовательность:
в исходную
последовательность:
Ранее нами описаны [1] такие сети на основе НЭ с бинарным нелинейным преобразованием, обладающие рядом интересных свойств: ассоциативной обработки информации, запоминания, структурной обработки и распознавания информации и др.
Ассоциативность обращения к информации. Преобразование F обладает свойством ассоциативности обращения к точкам траектории А ассоциацией по n-членному фрагменту последовательности А: любой n-членный фрагмент сразу же адресует нас к соответствующей точке траектории.
Преобразование входной последовательности сигналов в многомерное сигнальное пространство, а также особенности ее обработки в этом пространстве являются следствием основного свойства НЭ, являющегося структурной единицей ДАЗУ, — свойства учета временной структуры входной последовательности. Появление этого свойств стало возможным благодаря использованию в модели нейрона большего числа свойств биологического нейрона.
Для постсинаптического потенциала на ячейке обобщенного дендрита — регистре сдвига НЭ — можно принять [2]:
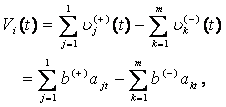
где ![]() и
и ![]() —
соответственно возбуждающий и тормозной постсинаптические потенциалы (ПСП),
возникающие на положительном и отрицательном единичном синаптических контактах
в пределах ячейки; at — входы на
эти
синапсы в течение интервала времени dt [в
интервале (t – dt/2,
t + dt/2)] b(+) и b(-)
— весовые связи элементарных единичных контактов.
—
соответственно возбуждающий и тормозной постсинаптические потенциалы (ПСП),
возникающие на положительном и отрицательном единичном синаптических контактах
в пределах ячейки; at — входы на
эти
синапсы в течение интервала времени dt [в
интервале (t – dt/2,
t + dt/2)] b(+) и b(-)
— весовые связи элементарных единичных контактов.
Суммарный ПСП, достигший тела клетки, будет равен сумме ПСП, пришедших к телу клетки от соответствующих ячеек обобщенного дендрита со своими задержками. Для ближайшей к соме ячейки эта задержка равна dt, далее — 2dt, 3dt и т. д. Тогда суммарный ПСП на теле клетки будет равен сумме
![]()
или иначе
![]() (5)
(5)
где bi — весовой коэффициент, характеризующий знак синаптического контакта; at-i — сигналы, приходящие по афферентному волокну в последовательные моменты времени.
При использовании пороговой функции НЭ откликается на фрагменты входной последовательности при выполнении порогового условия:
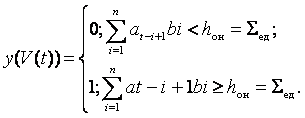
Здесь порог острой настройки ![]() равен числу единиц в адресе
нейрона
равен числу единиц в адресе
нейрона ![]() .
.
Ассоциативность обращения позволяет сохранить топологию преобразуемой информации. Действительно, одинаковые фрагменты последовательности преобразуются в одну и туже траекторию, разные — в различные, причем близкие в перцептивном пространстве фрагменты последовательности преобразуются в близкие траектории.
Запоминание. НЭ, изменяющие свое состояние при обучении, например
за счет изменения весов связей [1,3], может служить элементом памяти. НЭ,
например, может запоминать символ последовательности at+1
непосредственно следующий за адресным n-членным
фрагментом ![]() в текущий момент времени t, находящимся в окне длины n,
т. е. в регистре сдвига. Это равносильно введению в вершинах гиперкуба Ge функции памяти М, ставящей в
соответствие каждой вершине
в текущий момент времени t, находящимся в окне длины n,
т. е. в регистре сдвига. Это равносильно введению в вершинах гиперкуба Ge функции памяти М, ставящей в
соответствие каждой вершине ![]() , соответствующей t-му символу последовательности А, двоичную
переменную at+1; являющуюся
(t + 1)-м символом некоторой двоичной
последовательности А:
, соответствующей t-му символу последовательности А, двоичную
переменную at+1; являющуюся
(t + 1)-м символом некоторой двоичной
последовательности А:
![]()
Можно осуществить восстановление исходной последовательности А по
обусловленной ею траектории ![]() и несущей последовательности
и несущей последовательности ![]() . Или, что
то же самое, по одной из точек траектории:
. Или, что
то же самое, по одной из точек траектории: ![]() .
.
Можно заменить детерминированную функцию памяти М стохастической,
которая позволяет характеризовать каждую вершину траектории с точки зрения частоты
появления во входной информации сочетания ![]() , введением счетчиков,
запоминающих число прохождений данной вершины в данном направлении.
, введением счетчиков,
запоминающих число прохождений данной вершины в данном направлении.
При запоминании счетчики изменяют свои состояния в зависимости от направления перехода:
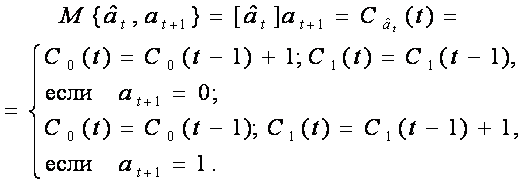
При этом применение порогового преобразования по запоминанию H позволяет воспроизводить информацию заданной степени достоверности.
При воспроизведении анализируются состояния этих счетчиков и текущий символ формируется в зависимости от выполнения порогового условия:
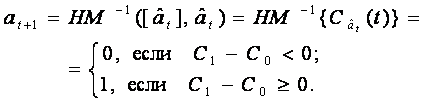
Отображение F является основой для осуществления структурной обработки информации. Действительно, в последовательности А среди n-членных фрагментов может встретиться уже ранее встречавшийся, и траектория в этом случае пройдет через вершину, уже принадлежащую ей, т. е. пересечется сама с собой.
Если с использованием преобразования F проанализировать класс последовательностей {А}, в
которых в разных комбинациях встречаются последовательности {Bi}, и применить к ним пороговое
преобразование, в n-мерном сигнальном
пространстве мы сформируем множество траекторий ![]() , соответствующее
множеству последовательностей {Bi},
т. е. словарь.
, соответствующее
множеству последовательностей {Bi},
т. е. словарь.
Наличие сформированного словаря часто встречающихся событий может быть использовано для детектирования старой информации в потоке новой. В этом случае происходит поглощение фрагментов входных последовательностей A, соответствующих словам словаря, и пропускание новой относительно словаря информации, что позволяет реализовать структурный подход к обработке информации.
Для этого необходимо модифицировать преобразование F-1
для приобретения им детектирующих свойств. В результате действия
модифицированного преобразования ![]() при взаимодействии некоторой
входной последовательности
при взаимодействии некоторой
входной последовательности ![]() , содержащей наряду со старой
некоторую новую информацию, со сформированной ранее траекторией
, содержащей наряду со старой
некоторую новую информацию, со сформированной ранее траекторией ![]() организуется
последовательность C, в которой заменяются
нулями части последовательности
организуется
последовательность C, в которой заменяются
нулями части последовательности ![]() траектории
траектории ![]() ,
совпадающие с частями траектории
,
совпадающие с частями траектории ![]() . Другими словами, во входной
последовательности
. Другими словами, во входной
последовательности ![]() заменяются нулями символы,
соответствующие которым точки траектории
заменяются нулями символы,
соответствующие которым точки траектории ![]() совпадают с точками
сформированной ранее траектории
совпадают с точками
сформированной ранее траектории ![]() :
:
![]()
где
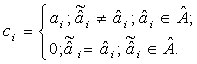
Если на основании множества входных последовательностей A ранее был сформирован словарь ![]() , то использование
преобразования
, то использование
преобразования ![]() позволяет сформировать так
называемую синтаксическую последовательность (СП) или последовательность
аббревиатур C, характеризующую связи слов L словаря {L} в
последовательности
позволяет сформировать так
называемую синтаксическую последовательность (СП) или последовательность
аббревиатур C, характеризующую связи слов L словаря {L} в
последовательности ![]() .
.
Тем самым создается предпосылка для построения многоуровневой структуры,
в которой синтаксическая последовательность C,
содержащая только новую, по отношению к данному уровню, информацию, становится
входной для следующего уровня, где, подобно описанному выше, из множества синтаксических
последовательностей {C} формируется поуровневый
словарь ![]() и
множество синтаксических последовательностей следующего уровня {E}.
и
множество синтаксических последовательностей следующего уровня {E}.
Распознавание. Под распознаванием в данных терминах понимается
процесс принятия решения о степени совпадения входной информации с ранее
запомненной. В основе механизма распознавания лежит сравнение входной
последовательности ![]() и наиболее близкой ей из
запомненных последовательностей — последовательности А, которая начинает
воспроизводиться с помощью преобразования HM-1MF в ответ на входную
последовательность
и наиболее близкой ей из
запомненных последовательностей — последовательности А, которая начинает
воспроизводиться с помощью преобразования HM-1MF в ответ на входную
последовательность ![]() , с вычислением некоторой меры
близости:
, с вычислением некоторой меры
близости:
![]() .
.
Вычисление D осуществляется суммированием расстояния между соответствующими n-членными фрагментами входной и воспроизводимой последовательностей, полученных на каждом шаге:

где T — длина траектории.
Распознается входная последовательность, для которой суммарное расстояние
D между вершинами ![]() входной и запомненной
траекторий меньше порога по распознаванию:
входной и запомненной
траекторий меньше порога по распознаванию:
![]()
Расфокусированное преобразование. Если вместо порога острой настройки используется меньший порог, то на текущий входной n-членный фрагмент входной последовательности отвечает не только НЭ с соответствующим адресом, но и другие НЭ, лежащие в некоторой окрестности радиуса r точки пространства с этим адресом:
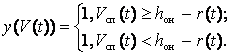
При этом число отвечающих нейронов
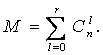
Это так называемое расфокусированное преобразование F(r), которое осуществляет расфокусированное отображение входной последовательности в трубку траекторий радиуса г с центром в исходной траектории.
1. Динамическая нейронная сеть на основе НЭ с сигмоидной функцией
Расширим понятие ДНС с вышеописанными свойствами использованием НЭ, имеющих небинарный выход. Назовем такую нейронную сеть континуальной. Ее активность точно соответствует активности бинарной сети, но она способна осуществлять более сложные функции, так как ее НЭ не ограничены бинарными значениями, а архитектура — более сложная.
Использование сигмоидной функции приводит к расширению понятия преобразования F в n-мерное пространство. В этом случае можно говорить о модифицированном отображении Fs:
![]()
которое
вместо траектории формирует трубку траекторий ![]() , ярко светящуюся в области
основной траектории
, ярко светящуюся в области
основной траектории ![]() и плавно затухающую к
периферии (в соответствии с характеристикой сигмоидной функции). При
запоминании механизм стохастической обработки также модифицируется. Счетчики
переходов заменяются одним реверсивным счетчиком. Формируется трубка,
содержащая информацию о входной последовательности, которая также имеет
максимальное значение в центре трубки и затухает к ее периферии. Сформированный
при обучении след устойчив к разрушающим воздействиям (обладает голографическими
свойствами — в любой части единичного гиперкуба содержится информация о входной
последовательности). При формировании словаря слова формируются как пересечения
таких трубок. Особенно сильно влияет модификация преобразования на
распознавание. Отклик формируется как сумма откликов всех нейронов сети со
своим весом, равным значению сигмоидной функции на данном нейроне.
и плавно затухающую к
периферии (в соответствии с характеристикой сигмоидной функции). При
запоминании механизм стохастической обработки также модифицируется. Счетчики
переходов заменяются одним реверсивным счетчиком. Формируется трубка,
содержащая информацию о входной последовательности, которая также имеет
максимальное значение в центре трубки и затухает к ее периферии. Сформированный
при обучении след устойчив к разрушающим воздействиям (обладает голографическими
свойствами — в любой части единичного гиперкуба содержится информация о входной
последовательности). При формировании словаря слова формируются как пересечения
таких трубок. Особенно сильно влияет модификация преобразования на
распознавание. Отклик формируется как сумма откликов всех нейронов сети со
своим весом, равным значению сигмоидной функции на данном нейроне.
Континуальная ДНС имеет ту же топологию, что и бинарная. Единственное отличие заключается в использовании вместо пороговой функции, описываемой выражением
![]()
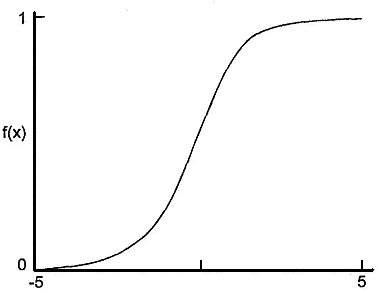
сигмоидной функции (см. рисунок):
![]()
В этом случае если значения V(t) существенно ниже порога h = 0, значения f(V(t)) почти равны нулю. Для значений V(t), которые существенно превышают порог h = 0, значения f(V(t)) близки к 1.
Заменим счетчики C0 и C1 числа прохождений заданной вершины в заданном направлении одним реверсивным счетчиком C, который изменяет свои состояния в сторону уменьшения для переходов в "0" и в сторо ну увеличения — для переходов в "1". При этом функция памяти принимает вид:
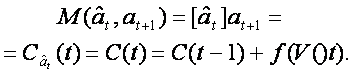
При воспроизведении анализируется состояние счетчика и текущий символ формируется в зависимости от выполнения порогового условия:
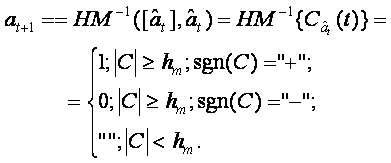 (1)
(1)
Здесь ![]() — вершина сигнального
пространства; первые две строчки условий выполняются хотя бы для одного из 2т
НЭ; “ ” — означает неопределенное состояние. Изменяя значение порога
по памяти hm, можно формировать словарь более или менее
достоверно встречающихся событий. Или, что то же самое, запоминать более или
менее достоверную входную информацию. Если hm
= 1, мы запоминаем входную информацию по одному предъявлению.
— вершина сигнального
пространства; первые две строчки условий выполняются хотя бы для одного из 2т
НЭ; “ ” — означает неопределенное состояние. Изменяя значение порога
по памяти hm, можно формировать словарь более или менее
достоверно встречающихся событий. Или, что то же самое, запоминать более или
менее достоверную входную информацию. Если hm
= 1, мы запоминаем входную информацию по одному предъявлению.
Забывание в этом случае реализуется следующим образом:
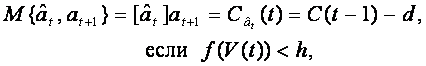
где d — константа.
Обученная сеть из таких НЭ воспроизводит запомненную ранее информацию. Любой фрагмент входной последовательности вызывает отклик в одном из НЭ, если выполняется условие по памяти (1). Отклик НЭ означает наличие записанного в нем перехода в «0» или в «1», добавление которого к исходному фрагменту адресует нас к следующему НЭ и т. д., пока мы не попадем в НЭ с откликом « ». В этом месте воспроизведение прерывается.
В случае использования расфокусированного преобразования в процесс распознавания включаются и нейроны с отличными от исходного адресами. В этом случае

2. Информационные характеристики сети из континуальных НЭ
Оценим эффективность этого способа реализации ДАЗУ по сравнению с предыдущим, для чего используем понятие коэффициента эффективности E [4], который в случае рассматриваемой сети можно интерпретировать как число разрядов памяти, необходимых для записи одного бита информации. Будем считать для простоты, что пластичность бинарная, а ДАЗУ — автоассоциативное, с памятью в виде триггера.
Мы рассматриваем случай реализации динамической сети по полному алгоритму, где имеется 2n нейроподобных элементов — вершин и-мерного сигнального пространства. В этом случае имеется нейронная пластичность, так как при обучении все синаптические связи одновременно меняют свои значения, если память реализуется за счет изменения весов связей.
Пусть один эталон длины L символов
записывается в одно ДАЗУ, тогда состояние информационного источника задается
набором из L бинарных эталонных векторов ![]() ,
размерности n. Предполагается, что L << 2n, т. е. мы пренебрегаем вероятностью того, что
некоторый вектор может встретиться в наборе
,
размерности n. Предполагается, что L << 2n, т. е. мы пренебрегаем вероятностью того, что
некоторый вектор может встретиться в наборе ![]() несколько раз (т. е. что
траектории в сигнальном пространстве пересекаются). Поскольку словарь сети
состоит из М эталонов-образов, имеется на самом деле
несколько раз (т. е. что
траектории в сигнальном пространстве пересекаются). Поскольку словарь сети
состоит из М эталонов-образов, имеется на самом деле ![]() бинарных векторов,
но при достаточно большой размерности сигнального пространства все равно выполняется
условие
бинарных векторов,
но при достаточно большой размерности сигнального пространства все равно выполняется
условие ![]() .
.
Процедура обучения сводится к подаче на вход системы последовательности эталонных векторов. В первом случае состояние активации задается бинарным числом, т. е. процедура кодирования соответствует переходу НЭ в некоторое состояние, зависящее от вектора связей и от состояния источника, т. е. набора векторов X.
Используется процедура сложного декодирования, когда информация о последующих векторах набора X зависит от информации о предыдущих распознанных векторах.
Каждый НЭ ДАЗУ активируется в ответ строго на свой адрес. Этим
обеспечивается независимость активации отдельных НЭ и, следовательно, близость
коэффициента эффективности сети к коэффициенту эффективности отдельного НЭ. В
этом случае вектор связей известен полностью, поэтому из анализа, приведенного
в [4], коэффициент эффективности каждого НЭ, а следовательно, и всей сети,
равен ![]() .
Здесь
.
Здесь ![]() —
длина эталонной последовательности; S
—
длина эталонной последовательности; S![]() — степень
заполнения сети (в нашем случае составляет 0,001 всего объема сети).
— степень
заполнения сети (в нашем случае составляет 0,001 всего объема сети).
В случае сети с сигмоидальной нелинейностью коэффициент эффективности сети будет также близок к коэффициенту эффективности отдельного НЭ, поскольку каждый эталон записывается в отдельное ДАЗУ, а соседние фрагменты последовательности отображаются в отдаленные области сигнального пространства.
Применение НЭ с сигмоидальной нелинейностью похоже на эффект расфокусировки, только воздействие не такое грубое, как в случае расфокусировки: вместо введения в процесс соседних нейронов из r-окрестности исследуемой вершины мы используем все НЭ, но в степени, зависящей от их расстояний до исследуемого адреса.
Оценим коэффициент эффективности сети в этом случае. При записи
информации возникает эффект голографичности памяти: информацию помнят все НЭ (с
разной степенью силы). Сила эта зависит от экспоненциальной константы C и изменяется от прямой пропорциональности до пороговой
функции. Коэффициент эффективности сети увеличивается от значения ![]() в
последнем случае до
в
последнем случае до ![]() — в первом, где K — некоторая константа, зависящая от угла наклона
пологого участка сигмоидной функции. Естественно, при этом в такое же число раз
увеличивается надежность хранения информации.
— в первом, где K — некоторая константа, зависящая от угла наклона
пологого участка сигмоидной функции. Естественно, при этом в такое же число раз
увеличивается надежность хранения информации.
Введение сигмоидальной нелинейности определяет появление в сети свойства восстановления информации по ее части при распознавании. Действительно, даже при отсутствии информации о продолжении траектории в ожидаемой точке мы можем ее извлечь из всех оставшихся точек пространства.
Использование динамического распределения памяти [2] при реализации сети позволяет получить тот же коэффициент эффективности сети, что и при полном объеме используемой памяти с учетом доли выделенных при динамическом распределении памяти НЭ.
* * *
В статье представлен случай использования НЭ с сигмоидальным нелинейным преобразованием в динамической нейронной сети. Это позволяет при сохранении основных свойств сети (ассоциативного обращения к информации, запоминания, воспроизведения и распознавания и др.), а также структурного анализа информации увеличить эффективность сети по хранению информации и надежность хранения за счет появления голографических свойств памяти.
Список литературы
1. Харламов А. А. Нейроподобные элементы с временной суммацией входного сигнала и блоки ассоциативной памяти на основе этих элементов // Вопросы кибернетики. Устройства и системы. Под ред. Н. Н. Евтихиева. М.: МИРЭА, 1983. С. 57—68.
2. Харламов А. А. Нейроподобные элементы с временной суммацией входных сигналов и ассоциативная память на их основе // Информационные технологии. 1997. № 8. С. 40—44.
3. Hebb D. D. Organization of Behavior. N. Y. 1949. 335 p.
4. Фролов А. А., Муравьев И. П. Нейронные модели ассоциативной памяти. М.: Наука, 1987. 161 с.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 10, 1998
НЕИРОСЕТИ И НЕЙРОКОМПЬЮТЕРЫ
Ключевые слова: Динамические нейронные сети, пороговые функции, сигмоидальное преобразование, временное накопление сигнала.
Публикации с ключевыми словами: Динамические нейронные сети, пороговые функции, сигмоидальное преобразование, временное накопление сигнала
Публикации со словами: Динамические нейронные сети, пороговые функции, сигмоидальное преобразование, временное накопление сигнала
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



