научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#8 август 2005
А. Ю. Щеглов, д-р техн. наук проф., СПб ГИТМО (ТУ)
Векторные интерпретация и метод решения задачи линейного программирования
Рассматривается интерпретация задачи линейного программирования как пошаговой задачи многокритериальной оптимизации. Приводится векторная интерпретация аддитивного критерия оптимальности как приведенной длины проекции вектора варианта на идеальный вектор качества в пространстве критериев, откуда вводится векторная интерпретация задачи линейного программирования. Рассматривается метод решения задачи в рамках приведенной векторной интерпретации.
Интерпретация задачи линейного программирования как пошаговойзадачи многокритериальной оптимизации
Задача линейного программирования в общем виде может быть представлена следующим образом: найти Xn, n = 1, ..., N, такие, что
![]()

при условии, что
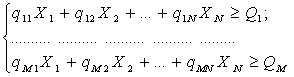
при Xn ≥ 0, n = 1, ..., N. При необходимости дополняется условие целочисленности всех Xn.
Рассмотрим интерпретацию задачи линейного программирования как пошаговую задачу многокритериальной оптимизации. В общем случае задача многокритериальной оптимизации может быть сформулирована следующим образом. Задано N вариантов системы с номерами n = 1, ..., N, каждый из которых характеризуется М параметрами (или частными критериями качества) qnm с номерами m = 1, ..., М. Требуется выбрать вариант, превосходящий остальные варианты по совокупности параметров. В качестве критерия оптимальности (или агрегатирующего показателя качества) на практике, как правило, используется аддитивная свертка нормированных значений параметров
 (1)
(1)
где qnm — по какому-либо правилу нормированные (приведенные к безразмерному виду) значения разнородных параметров. В случае необходимости учета различной относительной важности параметров в формуле (1) используются коэффициенты относительной важности параметров (или весовые коэффициенты) βm, где 0 ≤ βm ≤ 1, имеем

Задача линейного программирования может интерпретироваться как задача многокритериальной оптимизации в следующем смысле [1, 2]. Задано N вариантов, характеризуемых М параметрами qnm с номерами m = 1, ..., М. На каждом шаге требуется выбрать оптимальный вариант (план) из заданного множества, состоящего из N вариантов. Оптимальность здесь понимается в смысле наилучшего достижения совокупности ограничений Qm, m = 1, ..., М, при использовании выбранного варианта. Если рассмотреть некоторый произвольный шаг оптимизации, то он отличается от предыдущего лишь тем, что требуется уже выполнить не исходные ограничения Qm, а в общем случае ограничения, задаваемые меньшими значениями, с учетом полученных на предыдущих шагах результатов. Для рассматриваемого шага решаем многокритериальную задачу оптимизации в известной постановке — выбрать оптимальный вариант по совокупности М параметров. При этом очевидно, что реализуемый метод нормирования параметров должен учитывать, в какой мере для каждого шага достигаются заданные ограничения Qm.
Таким образом, на каждом шаге из сравниваемых N вариантов (частных планов) требуется выбрать такой вариант n (т. е. придать положительное приращение соответствующей переменной Хn), для которого по сравнению с остальными вариантами решений из исходного множества N для рассматриваемого шага оптимизации наилучшим образом обеспечивается выполнимость ограничений Qm в том смысле, что для выбранного Хn для всех М имеем минимальные разности Qm — qnm (если для всех М выполняется Qm — qnm = 0, задача решена). Проблема многокритериальности задачи, требующая решения, здесь состоит в том, что для одного варианта n могут быть минимальными разности Qm — qnm по параметру m, в то время как для другого варианта, например n’ — по параметру m'. Возникает задача — какой из вариантов n или n' в рассматриваемом случае признать оптимальным, и почему.
Векторная интерпретация задачи линейного программирования
В основу векторной интерпретации задачи линейного программирования может быть положена векторная интерпретация задачи многокритериальной оптимизации и предложенная нами векторная интерпретация аддитивного агрегатирующего критерия как приведенной длины проекции вектора качества варианта на идеальный вектор качества в пространстве критериев RM. В основу предлагаемого подхода положен подход, рассмотренный в [3], для выбора нехудших вариантов в векторном пространстве, состоящий в учете при оптимизации вариантов одновременно двух критериев — длины вектора качества варианта Хn и угла между векторами варианта и идеальным вектором
 (2)
(2)
 (3)
(3)
при условиях
выбора оптимального варианта ![]() , что имеет физический смысл
выбора нехудших решений, качество которых в M-мерном
пространстве отображается векторами, имеющими максимальную длину и наилучшим
образом совпадающими по направлению с заданным идеальным вектором.
, что имеет физический смысл
выбора нехудших решений, качество которых в M-мерном
пространстве отображается векторами, имеющими максимальную длину и наилучшим
образом совпадающими по направлению с заданным идеальным вектором.
Данный подход, наряду с методом Паретто, представляет чисто теоретический
интерес, так как на практике использование обоих критериев оптимальности
существенно усложняет задачу оптимизации и, как правило, позволяет найти
множество "нехудших решений", практически не уступающему по величине
исходному множеству сравниваемых альтернатив. В [4—9] в качестве критерия
оптимальности нами предлагается использовать параметр "длина проекции
вектора качества варианта на идеальный вектор" Xn0,
который позволяет одновременно учитывать оба параметра Хn и ![]() , т. е. свести задачу оптимизации
к однокритериальной
, т. е. свести задачу оптимизации
к однокритериальной
![]() (4)
(4)
при условии
выбора оптимального варианта ![]() . В [4] строго доказывается, что
в ортонормированном базисе вместо длины проекции на идеальный вектор может
рассматриваться аддитивная свертка нормированных значений параметров,
представляющая собой сумму нормированных параметров вариантов, использование
которой существенно упрощает решение задачи при векторной ее интерпретации.
. В [4] строго доказывается, что
в ортонормированном базисе вместо длины проекции на идеальный вектор может
рассматриваться аддитивная свертка нормированных значений параметров,
представляющая собой сумму нормированных параметров вариантов, использование
которой существенно упрощает решение задачи при векторной ее интерпретации.
Действительно, с учетом того, что в ортонормированном базисе нормированные значения параметров идеального вектора q0m = 1, m = 1,..., М, подставляя (2) и (3) в (4), получаем

соответственно из (1) имеем
![]()
откуда следует, что аддитивная свертка параметров представляет собой приведенную или умноженную на коэффициент (М)1/2 длину проекции вектора качества варианта на вектор качества идеального варианта в ортонормированном пространстве критериев RM. Так как значение (M)1/2 совпадает для всех вариантов, т. е. не влияет на результат сравнительного анализа, будем считать, что критерий оптимальности задается формулой (1) и имеет физический смысл длины проекции вектора качества варианта на идеальный вектор качества.
Теперь остановимся на вопросах синтеза ортонормированного базиса и векторной интерпретации использования весовых коэффициентов βm. При объективном способе нормирования параметров [4, 9] в качестве идеальных выбираются лучшие значения параметров на сравниваемом множестве вариантов n = 1,..., N, задаваемые в рассматриваемом случае формулой
![]()
причем на сравниваемом множестве вариантов n = 1,..., N корректируются значения параметров, качество которых превосходит задаваемое (или требуемое) идеальное — приравнивается задаваемому идеальному. Нормированные значения параметров задаются формулами
![]()
Задание весовых коэффициентов может быть интерпретировано следующим образом: изменение весовых коэффициентов параметров изменяет направление и длину гипотетически идеального вектора в пространстве критериев. При этом изменяются и длины проекций векторов вариантов на идеальный вектор, т. е. значения аддитивного критерия оптимальности.
Теперь, с учетом предложенной интерпретации задачи линейного программирования как пошаговой многокритериальной задачи оптимизации, для которой, в свою очередь, нами дана векторная интерпретация (в частности, предложена векторная интерпретация аддитивного критерия оптимальности), рассмотрим векторную интерпретацию задачи линейного программирования. Векторная интерпретация задачи на плоскости (в пространстве RM = 2) проиллюстрирована на рис. 1.

Рис. 1. Иллюстрация векторной интерпретации задачи линейного программирования на плоскости
Здесь по осям координат, где откладываются параметры для различных вариантов плана qm, отложены и ограничения Qm. В приведенной системе координат получаем вектор <OO'>, образующий идеальное направление "продвижения в пространствеев" для выполнения заданных ограничений (идеальность направления соответствует равенству Qm в исходной системе ограничений). Два возможных плана (N = 2) отображаются в рассматриваемом пространстве векторами, например <ОО1> и <OO2>. Метод поэтапного получения оптимального плана (векторный метод планирования) состоит в выборе на каждом этапе оптимизации лучшего вектора по критерию длины проекции вектора варианта на идеальный вектор (OO') с переносом системы координат в направлении и на величину выбранного на очередном этапе оптимизации вектора. В частности, на рис. 1 лучшим для рассматриваемого этапа составления плана при наличии двух вариантов будет вариант, отображаемый вектором <ОО1>. Отложив этот вектор, получим новую систему координат и соответствующий ей новый идеальный вектор (O*O'), который примем в качестве вектора, задающего идеальное направление для следующего этапа. Многоэтапная процедура завершается при выполнении ограничений по всем видам задач. Набор отложенных векторов на всех этапах оптимизации (и соответственно отображаемые ими возможные частные планы) и составляют оптимальный план.
Замечание. При альтернативной постановке задачи линейного программирования — найти Хn, n = 1,..., N, такие, что

при условии, что

необходимо,
наоборот, достигнуть разрешенной области за максимальное число шагов. Здесь
критерием оптимальности также остается параметр ![]() , но условием выбора оптимального
плана уже будет
, но условием выбора оптимального
плана уже будет ![]() min для
каждого этапа оптимизации, причем оптимизация будет заканчиваться выполнением
предпоследнего шага — на последнем вектор пересечет запретную область.
min для
каждого этапа оптимизации, причем оптимизация будет заканчиваться выполнением
предпоследнего шага — на последнем вектор пересечет запретную область.
Таким образом, на каждом шаге выбора оптимального плана в качестве критерия оптимальности используется аддитивная свертка нормированных значений параметров

где нормированные значения параметров определяются по формуле
![]()
а весовые коэффициенты используются для того, чтобы учесть различие ограничений Qm. Очевидно, что приоритет планов здесь определяется приоритетами (в данном случае — значениями) ограничений и значениями коэффициентов Cn в целевой функции. Предположим, что величины Сn = 1 для всех N рассматриваемых вариантов. В данных предположениях имеем следующую формулу для расчета весовых коэффициентов:
![]()
где ![]() .
.
Именно это условие нами рассматривалось при использовании предлагаемого
подхода для решения систем линейных уравнений большой размерности [2] и для приложений
задач линейного программирования, используемых для решения задачи распределения
работ в мультипроцессорных системах, решаемых в рамках теории расписаний [1].
При различии значений Cn
аддитивным критерием ![]() должно учитываться и различие
величин Cn в том смысле, в
какой мере по сравнению с вариантом, характеризуемым
должно учитываться и различие
величин Cn в том смысле, в
какой мере по сравнению с вариантом, характеризуемым ![]() , увеличит значение
целевой функции любой иной n-й вариант. С учетом
сказанного имеем
, увеличит значение
целевой функции любой иной n-й вариант. С учетом
сказанного имеем
 (5)
(5)
где ![]() .
.
Векторная интерпретация использования коэффициента ![]() также связана с
изменением расположения области ограничений и, как следствие, идеального
вектора в пространстве критериев.
также связана с
изменением расположения области ограничений и, как следствие, идеального
вектора в пространстве критериев.
Пошаговый метод решения задачи
Пошаговый метод получения оптимального плана состоит в следующем. При выполнении каждого шага оптимизации необходимо проверять условие на выполнение заданных ограничений Qm. Если они не выполняются (выполняются не все) осуществляется очередной шаг, в противном случае — синтез оптимального плана завершен. При выполнении каждого шага оптимизации фиксируется выбранный оптимальный вектор, пересчитываются новые ограничения Qm (что эквивалентно отложению вектора в пространстве критериев), m = 1,..., М,

по формуле
(5) рассчитываются сравниваемые значения аддитивных критериев оптимальности,
где выбор оптимального варианта (частного плана) на каждом шаге осуществляется
из условия ![]() .
Формальным условием окончания выполнения пошаговой процедуры оптимизации будет
выполнение условия Qm: = 0, m = 1,..., M. Решением задачи
будет множество вариантов (оптимальный план), соответствующих отложенным на
всех шагах оптимизации оптимальным векторам.
.
Формальным условием окончания выполнения пошаговой процедуры оптимизации будет
выполнение условия Qm: = 0, m = 1,..., M. Решением задачи
будет множество вариантов (оптимальный план), соответствующих отложенным на
всех шагах оптимизации оптимальным векторам.
Из приведенных формул для расчета параметров оптимизации делаем вывод, что рассматриваемый метод легко реализуем на ЭВМ, а формулы характеризуются низкой сложностью вычислений; все вычисления сведены к пошаговому алгоритму.
Скажем несколько слов относительно вычислительной сложности предлагаемого метода. Следуя тому, что решаемая задача может быть отнесена к NP-полным, сложность методов, предназначенных для ее решения, оценивается из следующих соображений. Если обозначить через O сложность отдельных операций (вычитание, сложение, деление и т. д.), реализуемых на каждом шаге оптимизации l, l = 1,..., L, причем на каждом шаге требуется выполнить Ot операций, вычислительная сложность S численного метода определяется по формуле
 (6)
(6)
Сформулируем утверждения, доказывающие минимальную вычислительную сложность предложенного векторного метода.
Утверждение 1. Предлагаемый метод позволяет проводить оптимизацию за минимальное число шагов L.
Доказательство этого утверждения следует из того, что на каждом шаге выбирается оптимальный вариант, позволяющий наилучшим образом продвигаться в сторону допустимой области, что минимизирует число шагов L.
Замечание. Возможность уменьшения числа шагов состоит в том, чтобы не исходно задавать дискретное значение параметра Хn, например, принимать для каждого шага Хn = 1, а выбирать Хn таким, при котором n-решение для рассматриваемого шага остается оптимальным. Эта идея заложена, например, в симплекс - алгоритме, что не позволяет рассматривать этот метод как метод комбинаторного программирования. Аналогичный подход может быть применен и в рамках предложенного нами векторного метода [2]. Однако данные подходы приводят к резкому увеличению Ol, а как следствие, что видим из (6), и к резкому возрастанию параметра S (как правило, на каждом шаге оптимизации здесь уже требуется решать системы уравнений). Кстати говоря, именно поэтому в основе разработки численных методов оптимизации лежит идея уменьшения вычислительной сложности отдельного шага, несмотря на возможность увеличения их числа.
Утверждение 2. Предлагаемый метод позволяет проводить сравнительный анализ вариантов на каждом l-м шаге с минимальной вычислительной сложностью Ol.
Доказательство этого утверждения, рассматриваемое в [4—9], основано на том, что, во-первых, опарное сравнение вариантов на каждом шаге осуществляется только по одному параметру (а не по М), что существенно снижает трудоемкость каждого шага Ol, во-вторых, именно сравнение по одному параметру позволяет выбирать на каждом шаге не ограниченное множество "нехудших решений", а лучший вариант (в противном случае выражение (6) должно было бы учитывать, что на каждом шаге сложность вычислений не Оl, а rlOl, где rl — число "нехудших решений" на l-м шаге, причем значение rl должно в прогрессии увеличиваться при переходе к последующим шагам). Однако, платой за сведение задачи к однокритериальной является необходимость нормирования параметров и использование более сложных агрегатирующих критериев оптимальности. Нам удалось минимизировать сложность критерия оптимальности, дав его векторную интерпретацию и сведя задачу к возможности применения аддитивной свертки (кстати говоря, именно поэтому данный вопрос нами был ранее исследован столь подробно). Таким образом, "платой" за возможность сведения задачи к однокритериальной, что существенно упрощает вычисления (в десятки и сотни раз — в зависимости от размерности задачи), можно считать необходимость нормирования, реализуемого на каждом шаге единожды по достаточно простой формуле.
С учетом сказанного можем утверждать, что по параметру S, характеризующему вычислительную сложность численных методов, предназначенных для решения задач, относящихся к классу NP-полных, предложенный в работе векторный метод оптимизации обладает минимальной сложностью.
Таким образом, к достоинствам предлагаемого векторного метода решения задач линейного программирования можно отнести следующее:
· обеспечивает выбор оптимального плана на каждом шаге оптимизации (что гарантирует необходимость выполнения минимального числа шагов при синтезе планов);
· отличается простотой решения задачи в ее целочисленной постановке (на каждом шаге полностью откладывается вектор качества, что соответствует одной единице выбранной работы в оптимальном плане).
Численный метод точного решения задачи
Некоторые из приложений рассматриваемой задачи требуют либо точного ее
решения, либо решения с заданной точностью. Для точного решения задачи и
решения ее с заданной погрешностью результата может быть предложен двухэтапный
подход (предложенный для решения системы линейных уравнений большой размерности
в [2]). На первом этапе задача решается целочисленно, где оптимальные векторы
откладываются полностью. На втором этапе реализуется точное решение. При этом
решение получается уже в системе координат, получаемой для противоположного
квадранта, вершиной которой будет точка пересечения последнего отложенного на
первом этапе вектора с допустимой областью. Идеальный вектор получаем, соединяя
вершину координат с точкой (Qm, m = 1,..., М). Повторяем процедуру оптимизации, но
уже откладываем некоторые части k, k< 1, векторов в противоположном их исходным
направлениях, отложенные части к которых входят в оптимальный план уже с
отрицательным знаком. При выходе из допустимой области U возвращаемся к исходному квадранту системы координат,
уменьшаем части откладываемых векторов к, эти части оптимальных векторов уже
входят в искомый план с положительным знаком. Процедура с уменьшением
коэффициента к на каждом шаге выполняется до тех пор, пока не будет найдено точного
решения задачи. К достоинствам данного подхода, также ориентированного на
применение ЭВМ (ввиду простоты расчетных формул при сохранении пошагового
алгоритма оптимизации), можно отнести решение задачи с заданной точностью,
задаваемой ограничением допустимой области решений U не только, как и ранее, снизу, но уже и сверху — условием ![]() , которое для
решения задачи на плоскости проиллюстрировано на рис. 2. Данное условие
является формальным условием окончания решения задачи, что интерпретируется на
плоскости попаданием откладываемого вектора на последнем шаге второго этапа в
заштрихованную область U.
, которое для
решения задачи на плоскости проиллюстрировано на рис. 2. Данное условие
является формальным условием окончания решения задачи, что интерпретируется на
плоскости попаданием откладываемого вектора на последнем шаге второго этапа в
заштрихованную область U.

Рис. 2. Иллюстрация постановки задачи для решения с заданной точностью
Интерпретация и метод решения многокритериальной задачи линейного программирования
Отличие постановки многокритериальной задачи линейного программирования состоит в оптимизации одновременно нескольких L (l = 1,..., L) целевых функций. С учетом этого формальная запись многокритериальной задачи линейного программирования имеет следующий вид:

при условии, что

Задача оптимизации при такой постановке состоит в том, чтобы найти переменные, по возможности минимизирующие все целевые функции на единой допустимой области решений.
Рассмотрим постановку задачи на плоскости (М = 2). Пусть все М
ограничений Qm совпадают. Рассмотрим
в данных условиях две целевые функции: Х1 + ЗХ2
(соответственно имеем коэффициенты С11 = 1 и C21 = 3) и 2Х1 + Х2
(соответственно С12 = 2 и С22 = 1)- Используя
формулу (5), находим соответствующие коэффициенты ![]() . При этом для каждой целевой
функции получаем свою постановку задачи на плоскости в ортонормированном
базисе, соответственно свою допустимую область решений U1
(заметим, что именно в ортонормированном базисе, так как в исходном базисе допустимые
области решений совпадут) и свой идеальный вектор качества <ОО1>.
Совместим области допустимых решений и оптимальные векторы для различных целевых
функций в одной системе координат, что приведено на рис. 3. Очевидно, что
вектор <ОО1> является идеальным для первой целевой
функции и определяет крайне неэффективное решение для второй целевой функции
(его продолжение на рис. 3 до пересечения с допустимой областью решений U2). Аналогично можно сказать и о векторе <ОО2>,
но уже соответственно для второй целевой функции. Другими словами, если в
качестве идеального вектора взять, например, вектор <ОО1>
и с ним пошагово решить задачу оптимизации, то многокритериальная задача будет
решена при попадании в допустимую область U1
вектора, откладываемого на последнем шаге. Однако относительно полученного
решения можно утверждать следующее: оно оптимально для первой целевой функции и
крайне неудовлетворительно для второй. То же самое можно сказать и о векторе <ОО2>.
. При этом для каждой целевой
функции получаем свою постановку задачи на плоскости в ортонормированном
базисе, соответственно свою допустимую область решений U1
(заметим, что именно в ортонормированном базисе, так как в исходном базисе допустимые
области решений совпадут) и свой идеальный вектор качества <ОО1>.
Совместим области допустимых решений и оптимальные векторы для различных целевых
функций в одной системе координат, что приведено на рис. 3. Очевидно, что
вектор <ОО1> является идеальным для первой целевой
функции и определяет крайне неэффективное решение для второй целевой функции
(его продолжение на рис. 3 до пересечения с допустимой областью решений U2). Аналогично можно сказать и о векторе <ОО2>,
но уже соответственно для второй целевой функции. Другими словами, если в
качестве идеального вектора взять, например, вектор <ОО1>
и с ним пошагово решить задачу оптимизации, то многокритериальная задача будет
решена при попадании в допустимую область U1
вектора, откладываемого на последнем шаге. Однако относительно полученного
решения можно утверждать следующее: оно оптимально для первой целевой функции и
крайне неудовлетворительно для второй. То же самое можно сказать и о векторе <ОО2>.

Рис. 3. Иллюстрация векторной интерпретации многокритериальной задачи линейного программирования на плоскости
Таким образом, получаем задачу линейного программирования, определяемую в рассматриваемом случае допустимой областью решений U в ортонормированном базисе, являющейся объединением областей U1 и U2, и бесконечным множеством идеальных векторов, что проиллюстрировано на рис. 4. Вместе с тем на рис. 3 и рис. 4 явно выделяется один вектор — вектор <OO3>, характеризуемый тем, что если его рассматривать в качестве идеального, то его длина совпадает для обеих целевых функций. Другими словами, если вектор <ОО3> рассматривать в качестве идеального, то получаемое оптимальное решение характеризуется равной степенью оптимальности для различных целевых функций (не являясь в общем случае оптимальным ни для одной из целевых функций в отдельности, так как длина вектора <ОО3> превосходит длину вектора <OO1> и длину вектора <ОО2>. Такое решение будем называть равнооптимальным, а вектор <OO3> равноидеальным. В случае выбора равноидеального вектора задается равная важность целевых функций. При задании в качестве идеального вектора, идеального для конкретной целевой функции, максимально учитывается важность именно этой целевой функции. В общем случае, чтобы учесть более высокую относительную важность какой-либо целевой функции, необходимо в качестве идеального выбрать вектор, расположенный между равноидеальным вектором и вектором, идеальным для этой целевой функции (эти векторы являются граничными), которых, как следует из рис. 4, бесконечное множество. Сказанное является векторной интерпретацией и собственно методом учета относительной важности целевых функций для многокритериальных задач линейного программирования.
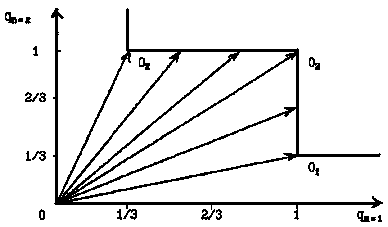
Рис. 4. Иллюстрация задания идеального вектора для многокритериальной задачи линейного программирования
Таким образом, многокритериальная задача линейного программирования решается так же, как и однокритериальная, с использованием пошагового метода. Отличие состоит исключительно в способе задания идеального вектора. Равноидеальный вектор определяется по следующей формуле:
![]()
учет же относительной важности целевой функции реализуется рассмотренным методом эвристически, например, на основе экспертных оценок.
* * *
В заключение отметим, что в работе представлен новый подход к интерпретации и решению задач линейного программирования. Учитывая простоту вычислительных операций, реализуемых при векторной интерпретации задачи как при условии целочисленности переменных, так и без такого условия, и простоту разработанного алгоритма пошаговой оптимизации в целом, можно надеяться на широкое использование метода в задачах оперативного планирования — в условиях жестких временных ограничений на продолжительность синтеза плана, в частности, для распределения работ в проблемно ориентированных вычислительных системах и ЛВС.
Список литературы
1. Щеглов А. Ю. Методика планирования распределения ресурсов вычислительной сети // Автоматика и вычислительная техника, 1989. № 1. С. 39—41.
2. Щеглов А. Ю. Векторная интерпретация и численный метод решения системы линейных уравнений // Изв. ВУЗов. Приборостроение, 1993. № 9—10. С. 36—44.
3. Кузьмин Б. И., Русин Ю. С. Векторная оптимизация систем и аппаратуры радиосвязи // Электросвязь, 1986. № 5. С. 30-32.
4. Щеглов А. Ю. Методика векторной оптимизации сложных подсистем информационно-вычислительных сетей // Автоматика и вычислительная техника, 1988. № 5. С. 14—19.
5. Щеглов А. Ю. Дополнительный критерий для формального выбора оптимального варианта ЛВС из множества "нехудших решений" // Автоматика и вычислительная техника, 1991. № 4. С. 39—41.
6. Щеглов А. Ю. Метод многокритериальной оптимизации сложных систем с экспертным заданием гипотетически идеального вектора качества // Изв. ВУЗов. Приборостроение, 1994. Т. 37. С. 21-23.
7. Щеглов А. Ю. Метод ограничений для оптимизации сложных систем // Радиотехника, 1993. № 4. С. 9—13.
8. Щеглов А. Ю. Метод поинтервального учета неравнозначности разнородных параметров альтернативных вариантов сложных систем вычислительной техники // Автоматика и вычислительная техника, 1990. № 6. С. 10—13.
9. Щеглов А. Ю. Статистический метод нормирования и учета относительной важности разнородных параметров для многокритериальной оптимизации сложных радиотехнических систем // Радиотехника, 1995. № 3. С. 7—8.
МЕТОДЫ ОПТИМИЗАЦИИ
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 8, 1998
Ключевые слова: Линейное программирование, многокритериальная оптимизация, векторное планирование, пошаговые методы.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



