научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#7 Июль 2005
В. В. Павлов, д-р техн. наук, проф., МГТУ "Станкин"
Полихроматические множества в теории систем. Операции над IIS-множествами
Представлен математический аппарат полихроматических множеств как новое средство информационных технологий в теории систем. Рассмотрены основные операции над ПS-множествами.
При моделировании сложных систем важное значение имеют операции над полихроматическими множествами, рассмотренными в [1]. Операции над ПS-множествами, осуществляемые с учетом их унитарных раскрасок и персональных раскрасок входящих элементов, более сложны, чем операции [2] над обычными множествами. В отличие от обычного множества, определяемого составом А своих элементов, IIS-множество в полном виде определяется шестеркой компонент:
![]() (1)
(1)
где А и F(a) — составы элементов и различных персональных цветов всех элементов; F(A) — множество унитарных цветов ПS - множества; [А х F(а)] — булева матрица персональных раскрасок элементов; [А х F(A)] — матрица персональных цветов элементов, одноименных с унитарными цветами ПS -множества; [А х A(F)] — булева матрица вариантов тел, реализующих унитарные цвета ПS - множества. При анализе и синтезе отдельного ПS - множества оно иногда может быть представлено сокращенными наборами компонент [3]:
дизъюнктивное множество — набором
![]() (2)
(2)
конъюнктивное множество — набором
![]() (3)
(3)
Отсутствие в (2) матрицы [А х A(F)] обусловлено тем, что в П![]() S-множестве
варианты тел унитарных цветов фактически представлены в матрице [А х F(A)], поскольку при
дизъюнктивной форме связи унитарный цвет Fj(A) существует при наличии хотя бы одного элемента ai
S-множестве
варианты тел унитарных цветов фактически представлены в матрице [А х F(A)], поскольку при
дизъюнктивной форме связи унитарный цвет Fj(A) существует при наличии хотя бы одного элемента ai ![]() А с персональным цветом Fj(ai) [1].
А с персональным цветом Fj(ai) [1].
Над IIS-множествами в форме (2), (3) может быть осуществлена
операция выделения подмножества ПSi ![]() ПS, так как
это подмножество состоит из элементов Ai
ПS, так как
это подмножество состоит из элементов Ai ![]() А и состав тел его унитарных
цветов является подмножеством тел унитарных цветов исходного ПS - множества. Выделение ПS,-осуществляется
двумя путями:
А и состав тел его унитарных
цветов является подмножеством тел унитарных цветов исходного ПS - множества. Выделение ПS,-осуществляется
двумя путями:
· задается состав Aj элементов ПSi после чего определяется состав F(Aj) его унитарных цветов, тела которых состоят из элементов Ai,
· задается состав F(Ai) унитарных цветов IISi, после чего определяется состав элементов тел, реализующих данные цвета — эти элементы и образуют состав Ai элементов выделяемого подмножества.
В первом случае выделяемое подмножество IISi получается единственным, а во втором случае возможны разные варианты решений, если существуют различные варианты тел унитарных цветов исходного ПS-множества. Рассмотрим, например, П^S-множество (рис. 1, а). Если условием выделения подмножества ПS,- является состав элементов Ai = (a1, а2, а3, a6), то в матрице [А х A(F)] этим элементам соответствуют только тела A1(F1) и A1(F4), поэтому выделяемое подмножество имеет состав унитарных цветов F(Ai) = (F1, F4) и будет единственным решением (рис. 1, б). Однако, если условием выделения подмножества будет состав унитарных цветов F(Ai) = (F1, F4), то этим цветам соответствуют тела A1(F1), A2(F1) и A1(F4) и возможны три варианта решения. При выборе тел A1(F1) и A1(F4) получим подмножество (рис. 1, б), а при выборе A2(F1) и А1(F4) получим подмножество (рис. 1, в) с составом элементов Ai = (а2, а3, a4, a5, a6) и унитарными цветами F(Ai) = (F1, F2, F3, F4); наконец, при выборе всех трех тел A1(F1), A2(F1) и A1(F4) решением будет само исходное множество (рис. 1, а).

Рис 1. Выделение подмножества из IIS-множества:
а — исходное ПS-множество; б, в — выделенные подмножества; • — элемент ci(j) = 1 булевой матрицы
В отличие от операции выделения подмножества, при вычислении разности, пересечения и объединения одновременно участвуют разные ПS-множества, поэтому возникает проблема идентификации элементов этих множеств в целях выявления эквивалентных элементов. Оказавшись в одном и том же ПS - множестве, все эквивалентные элементы — в силу закона идемпотентности [2] — будут поглощены и представлены единственным элементом.
При моделировании реальных систем эквивалентность элементов IIS-множества будет относительным понятием, зависящим от их влияния на определенные свойства системы, описываемые унитарными цветами IIS-множества. Наиболее строгим является условие эквивалентности ai, aj, основанное на равенстве составов и матриц взаимосвязи персональных цветов если
 (4)
(4)
менее строгим будет условие
![]() (5)
(5)
Если в рассматриваемом случае учитывается только определенный состав цветов FΔ(a), то условие эквивалентности ai aj определяется по отношению к этому составу цветов:
![]() (6)
(6)
Проблема идентификации элементов ПS-множества на предмет их эквивалентности решается с помощью булевой матрицы [А х F(a)] персональных раскрасок элементов этого множества. Сравнивая значения логических переменных в строках матрицы, соответствующих элементам ai, с заданным условием (4), (5) или (6), следует отметить, что каждое из этих условий требует разного уровня детализации описания персональных раскрасок элементов ПS-множества. Так, для проверки условия (6) достаточно описать только те персональные цвета аi и aj, которые относятся к заданному составу цветов Р\а), в то время как для проверки условия (5) необходимо описать все цвета F(ai) и F(aj); для проверки эквивалентности по условию (4) необходимо не только полное описание раскрасок, но и описание взаимосвязи всех цветов по условиям их существования с помощью матриц [F(ai) x F(ai)], [F(aj) x F(aj)].
Как правило, состав эквивалентных элементов IIS-множества сокращается по мере повышения уровня детализации описания их персональных раскрасок и перехода к более строгим условиям эквивалентности. Например, при технологическом проектировании детали (рис. 2, а) будут эквивалентными по составу обрабатываемых поверхностей — персональных цветов F(ai) и F(aj), так как для них выполняется условие (5). Однако при более детальном описании, с учетом матриц смежности поверхностей (рис. 2, б) детали ai и аj перестанут быть эквивалентными — условие (4) для них не выполняется.
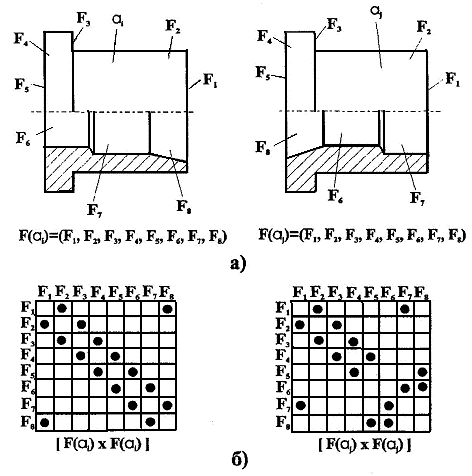
Рис. 2. Эквивалентность механообрабатываемых деталей:
а — обрабатываемые поверхности деталей аi, аj;б — матрицы смежности обрабатываемых поверхностей, • — элемент = 1 булевой матрицы
Поскольку в дизъюнктивных П![]() S - множествах матрицы [А х F(A)] и [А х F(a)] практически совпадают по составу цветов, то операция
объединения дизъюнктивных множеств
S - множествах матрицы [А х F(A)] и [А х F(a)] практически совпадают по составу цветов, то операция
объединения дизъюнктивных множеств
![]() (7)
(7)
может выполняться при представлении их в сокращенной форме (2) следующим образом:
· задается условие эквивалентности элементов исходных множеств и выявляются такие элементы в составе Aiи Аj
·
вычисляется состав А элементов итогового П![]() S
- ножества
S
- ножества
![]() (8)
(8)
·
вычисляется состав F(A) унитарных цветов П![]() S - множества
S - множества
![]() (9)
(9)
·
строится булева матрица [А х F(A)] П![]() S - множества
S - множества
![]() (10)
(10)
логические значения элементов ср(q) этой матрицы в зависимости от логических значений одноименных элементов в матрицах [Ai x F(Ai)] и [Aj х F(Aj)] вычисляются по формуле
![]() (11)
(11)
Операция объединения конъюнктивных множеств П^Si и П^Sj может выполняться только при представлении их в полной форме (1), поскольку:
· в объединяемых множествах одноименные элементы могут иметь в матрицах [Ai x F(Ai)] и [Aj х F(Aj)] несопоставимые составы унитарных цветов;
· персональные цвета элементов, принадлежащих разным множествам, могут порождать тела новых унитарных цветов, ранее не существовавших в F(Ai) и F(Aj).
При объединении конъюнктивных множеств
![]() (12)
(12)
состав унитарных цветов F(A) итогового множества ПS связан с составами F(a)i F(Ai) и F(a)j, F(Aj) соотношением
![]() (13)
(13)
Рассмотрим операцию объединения множеств П^Si и П^Sj на примере (рис. 3). Объединение выполняется следующим образом.
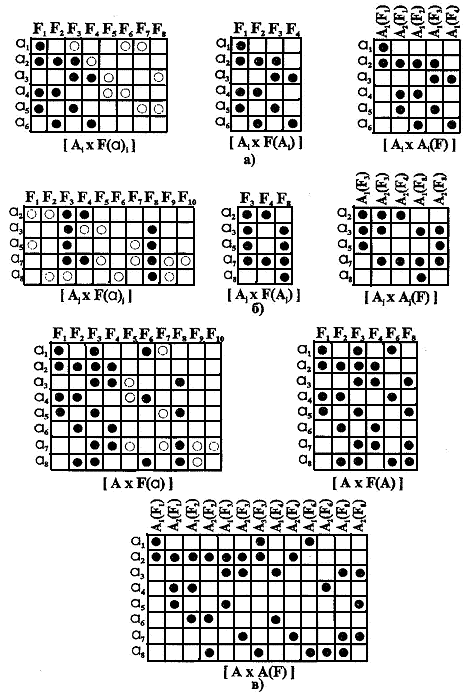
Рис. 3. Объединение полихроматических множеств:
а — матрицы [Аi х F(a)i], [Ai х F(Ai)], [Ai x Ai(F)] конъюнктивного множества П^Si; б — матрицы [Aj x F(a)j], [Aj x F(Aj)], [Aj x Aj(F)] конъюнктивного множества П^Sj; в — матрицы [А х F(а)], [А х F(A)], [A x A(F)] объединения П^Si и П^Sj; • — элемент сi(j) = 1 булевой матрицы, когда аi входит в состав тела A(Fj); о — элемент сi(j) = 1 булевой матрицы, когда аi - не входит в состав тела A(Fj)
1. Задается условие эквивалентности элементов исходных множеств и
выявляются элементы, отвечающие этому условию, в составе Ai
и Aj. Для определения эквивалентных
элементов сравниваются их персональные раскраски в матрицах [Aj х F(a)i] и [Aj x F(a)j]. Например, для элементов исходных множеств (рис.
3, а, б) условие эквивалентности принято соответствующим (5); сравнение
персональных раскрасок элементов в матрицах [Ai
х F(a)i] и [Aj x F(a)j] показывает, что эквивалентны элементы a2 ![]() Ai
и а2
Ai
и а2 ![]() Aj,
а3
Aj,
а3 ![]() Ai
и а3
Ai
и а3 ![]() Aj,
a5
Aj,
a5 ![]() Ai
и a5
Ai
и a5 ![]() Aj.
Aj.
2. Вычисляется состав А элементов итогового П^S - множества по формуле (8). В рассматриваемом примере

3. Вычисляется состав F(a) всех персональных цветов всех элементов П^Si и П^Sj по формуле
![]() (14)
(14)
В рассматриваемом примере

4. Строится булева матрица [А х F(a)] итогового П^S - множества
![]() (15)
(15)
Эта матрица строится объединением строк и столбцов матриц [Ai x F(a)i] и [Aj x F(a)j] — см. рис. 3, в. Логические значения элементов сp(q) матрицы в зависимости от логических значений одноименных элементов в объединяемых матрицах вычисляются по формуле (11).
5. Формируется булева матрица [А х A(F)] вариантов тел, реализующих унитарные цвета итогового П^S - множества, включающая в себя:
а) существовавшие в матрицах [Аi х Ai(F)] и [Aj х Aj(F)] варианты тел унитарных цветов F(Ai) и F(Aj); эта часть матрицы является объединением матриц вариантов тел унитарных цветов П^Si и П^Sj строится аналогично (15);
б) новые варианты тел, образованные из композиций элементов П^Si и П^Sj, в том числе тел, реализующих новые унитарные цвета, не существующие в F(Ai) и F(Aj). В рассматриваемом примере (рис. 3, в) в матрице [А х A(F)] появились новые тела A2(F2) и A3(F3) унитарных цветов F2, F3, существующих в F(Ai); кроме того, появились тела A1(F6), A2(F6), реализующие унитарный цвет F6(A), не существовавший ранее в F(Ai) и F(Aj).
Таким образом, состав тел в сформированной матрице [А х A(F)] может превосходить объединение составов тел из матриц [Ai x Ai(F)] и [Aj x Aj(F)]:
![]() (16)
(16)
Новые варианты тел унитарных цветов, как уже существующих в F(Ai) и F(Aj), так и не существовавших ранее, могут быть определены, если известны закономерности, определяющие взаимосвязь свойств элементов моделируемой системы; в противном случае возможность распознавания таких тел лежит в области поиска новых технических решений методами искусственного интеллекта или творческой деятельности человека.
6. По составу тел в матрице [А х A(F)] определяется состав F(A) унитарных цветов П^S - множества. В отличие от объединения дизъюнктивных множеств, где состав унитарных цветов определяется по формуле (9), при объединении конъюнктивных множеств имеет место
![]() (17)
(17)
Так, в примере (рис. 3) имеем
![]()
7. При известном составе элементов А и унитарных цветов F(A) формируется матрица [А х F(A)] исключением из матрицы [А х F(a)] столбцов, соответствующих персональным цветам в F(a), не породившим одноименных унитарных цветов в F(A).
Построением матрицы [А х F(A)] операция объединения П^Si и П^Sj завершается, поскольку все компоненты П^S в форме (1) определены.
При выполнении операций пересечения и разности ПS-множеств новые тела унитарных цветов не возникают, так как результатом выполнения этих операций являются подмножества исходных множеств. Поэтому, если проблема идентификации элементов множеств на предмет их эквивалентности решена, то операции пересечения и разности ПS-множеств можно выполнять при представлении их в сокращенной форме (2), (3).
Пересечением дизъюнктивных множеств П^Si и П^Sj будет множество
![]() (18)
(18)
являющееся общим подмножеством исходных множеств. Формирование пересечения (18) осуществляется так:
1. Задается условие эквивалентности элементов исходных множеств.
2. Определяется состав Aij элементов П^Si эквивалентных элементам П^Sj:
![]() (19)
(19)
Этот состав и образует пересечение П^Sij.
3. Формируется булева матрица [Aij x F(Aij)] исключением
из матрицы [Ai x F(Ai)] или [Aj х F(Aj)]
всех строк, соответствующих не вошедшим в Aij элементам, и столбцов, в которых не осталось ни одной
единицы. Оставшиеся столбцы определяют состав F(Ai-j)
унитарных цветов пересечения П![]() Sij —тем самым пересечение (18) сформировано.
Sij —тем самым пересечение (18) сформировано.
Формирование разности дизъюнктивных множеств
![]() (20)
(20)
осуществляется следующим образом:
1. Задается условие эквивалентности элементов исходных множеств.
2. Определяется состав Аij
элементов П![]() Si эквивалентных
элементам П
Si эквивалентных
элементам П![]() Sj — этот состав
образует пересечение П
Sj — этот состав
образует пересечение П![]() Sij.
Sij.
3. Вычисляется состав элементов Аi-j по формуле
![]() (21)
(21)
Этот состав и является составом элементов П![]() Si-j.
Si-j.
4. Формируется булева матрица [Ai-j х F(Ai-j)]
унитарных цветов разности исходных множеств (20) исключением из матрицы [Ai x F(Ai)]
всех строк, соответствующих вошедшим в Аij
элементам, и столбцов, в которых не осталось ни одной единицы. Оставшиеся
столбцы определяют состав F(Ai-j) унитарных цветов разности П![]() Si-j — тем самым разность (20)
дизъюнктивных множеств сформирована. Формирование разности
Si-j — тем самым разность (20)
дизъюнктивных множеств сформирована. Формирование разности
![]()
осуществляется
аналогичным образом. Состав элементов П![]() Si-j вычисляется по формуле
Si-j вычисляется по формуле
![]()
Пересечение конъюнктивных множеств П^Si и П^Sj
![]() (20)
(20)
из-за необходимости построения матрицы вариантов тел унитарных цветов F(Aij) определяется иначе, чем пересечения (18), а именно:
1. Задается условие эквивалентности элементов исходных множеств.
2. Определяется состав Aij элементов П^Si эквивалентных элементам П^Sj.
В тех случаях, когда установление эквивалентности элементов по матрицам [Ai х F(Ai)] и [Aj x F(Aj)]
затруднено, в формировании пересечения (22) используются и матрицы персональных
раскрасок элементов исходных множеств. Например, элементы a2
множеств Ai и
Aj (рис. 3,
а, б) в матрицах [Ai
x F(Ai)] и [Aj х F(Aj)]
имеют разные составы персональных цветов, одноименных с унитарными цветами F(Ai) и F(Aj), что не
позволяет сделать вывод об их эквивалентности по условию (5). Однако полные
составы персональных цветов этих элементов по матрицам [Ai x F(a)i] и [Aj x F(a)j] одинаковы и, следовательно, элементы а2
![]() Ai и а2
Ai и а2
![]() Aj эквивалентны по
условию (5). Поэтому в подобных случаях операция пересечения осуществляется при
представлении ПS-множеств в полной форме (1).
Aj эквивалентны по
условию (5). Поэтому в подобных случаях операция пересечения осуществляется при
представлении ПS-множеств в полной форме (1).
3. Если исходные множества представлены в полной форме (1), то после определения состава эквивалентных элементов Aij формируется булева матрица [Aij х F(a)ij] персональных раскрасок этих элементов исключением из матрицы [Ai x F(a)i] или [Aj х F(a)j] всех строк, соответствующих не вошедшим в Aij элементам, и столбцов, в которых не осталось ни одной единицы.
4. Формируется булева матрица [Ai-j x Ai-j(F)] тел унитарных цветов пересечения (22) исключением из матрицы [Ai x Ai(F)] или [Aj x Aj(F)] всех строк, соответствующих не вошедшим в Aij элементам, и столбцов, в которых утрачен требуемый состав тела унитарного цвета.
5. Формируется булева матрица [Aij x F(Aij)] исключением из матрицы [Ai x F(Ai)] или [Aj x F(Aj)] всех строк, соответствующих не вошедшим в Aij элементам, и столбцов, для которых в матрице [Aij х Aij(F)] нет вариантов тел данного унитарного цвета. Оставшиеся столбцы определяют состав F(Aij) унитарных цветов П^Sij — тем самым формирование пересечения (22) завершено.
Формирование разности конъюнктивных множеств
![]() (23)
(23)
осуществляется следующим образом:
1. Задается условие эквивалентности элементов исходных множеств.
2. Определяется состав Aij элементов П^Si эквивалентных элементам П^Sj, так же, как при определении Aij в пересечении (22).
3. Вычисляется состав элементов Аi-j по формуле (21) — он и является составом элементов разности П^Si-j.
4. Если исходные множества представлены в полной форме (1), то после определения состава элементов Ai-j разности (23) формируется булева матрица персональных раскрасок этих элементов вычеркиванием из матрицы [Ai х F(a)i] всех строк, соответствующих вошедшим в Аij (не вошедшим в Ai-j) элементам, и столбцов, в которых не осталось ни одной единицы.
5. Формируется булева матрица [Ai-1 x Ai-1(F)] тел унитарных цветов разности (23) исключением из матрицы [Аi х Ai(F)] строк, вошедших в Аij (не вошедшим в Ai-j), и столбцов, в которых утрачен требуемый состав тела унитарного цвета.
6. Формируется булева матрица [Ai-j x Ai-j(F)] исключением из матрицы [Ai x F(Ai)] строк, соответствующих вошедшим в Аij (не вошедшим в Ai-j) элементам, и столбцов, в которых в матрице [Ai-j х Ai-j(F)] нет вариантов тел данного цвета. Оставшиеся столбцы определяют состав F(Ai-j) унитарных цветов П^Si-j — тем самым формирование разности (23) завершено. Формирование разности
![]() (24)
(24)
осуществляется аналогичным образом. Состав элементов П^Si-j вычисляется по формуле
![]()
Симметрическая разность [2] множеств П^Si П^Sj определяется как объединение разностей (23), (24) этих множеств:
![]() (25)
(25)
Таким образом, операции над ПS-множествами отражают не только изменение состава их элементов, но и изменение раскраски самих множеств. Поскольку раскраска ПS-множества отражает свойства моделируемого объекта, операции над ПS-множествами открывают дополнительные возможности анализа и синтеза сложных систем.
Список литературы
1. Павлов В. В. Полихроматические множества в теории систем. Структура ПS-множеств // Информационные технологии. 1997. № 7. С. 11-16.
2. Куратовский К., Мостовский А. Теория множеств. М.: Мир, 1970, 416 с.
3. Павлов В. В. Полихроматические множества в теории систем. Изменение состава ПS-множеств // Информационные технологии. 1998. № 1. С. 4—8.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 3, 1998
ИНТЕЛЛЕКТУАЛЬНЫЕ СИСТЕМЫ
Ключевые слова
Теория систем, моделирование, полихроматические множества, раскраска множеств, выделение подмножеств, операции над множествами, матричные модели.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



