научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#7 Июль 2005
В. И. Левин, д-р техн. наук, проф, Пензенский технологический институт
Сравнение интервальных величин и оптимизация неопределенных систем
Введены отношения интервальных чисел, подобные отношениям вещественных чисел. Изучены их свойства, аналогичные свойствам отношений чисел. Определено понятие максимального (минимального) интервала. Установлено условие его существования и алгоритм нахождения. Показана возможность применения полученных результатов к решению задач оптимизации и управления систем с интервальными параметрами.
Введение
Существует обширная литература по интервальным вычислениям [1—3]. Большая ее часть касается вопросов рационального по точности вычисления функций с интервальными параметрами и обеспечению требуемой точности при решении систем уравнений. В существенно меньшей степени изучены вопросы сравнения и упорядочения значений функций с интервальными параметрами [4, 5] и их основа — сравнение интервальных чисел [5—8]. При этом сравнение интервальных чисел обычно выполняется с помощью отношений между ними, вводимых эвристически и в предположении, что это временные интервалы. Последнее приводит к появлению специфических отношений между интервалами, не обязательно присущих интервалам не временной природы.
В данной статье построена система сравнения интервальных чисел и выбора экстремального интервала, охватывающая интервальные числа любой природы. Система основана на введенных аксиомах сравнения интервальных чисел, аналогичных аксиомам сравнения вещественных чисел. Она приводит к формированию множества отношений интервальных чисел, аналогичных соответствующим отношениям вещественных чисел и обладающих почти всегда такими же свойствами. Построенная система удобна для решения многих классов прикладных задач с неточно известными параметрами — управления, измерения, контроля, оптимизации, принятия решений и т. д. Например, возможно решение в интервальной постановке задач математического программирования, задач оптимального управления и т. д. В отличие от других подходов к решению прикладных интервальных задач [4, 9—12] предлагаемый подход ориентируется не на какое-то одно сочетание значений параметров задачи внутри соответствующих интервалов (наихудшее сочетание при пессимистической стратегии, наилучшее — при оптимистической, усредненное — при центристской, ожидаемое — при вероятностной), а на все множество значений этих параметров.
1. Постановка задачи и математический аппарат
Будем изучать множества всевозможных интервальных чисел — как множества
всевозможных замкнутых интервалов ![]() ,…, каждый из которых
рассматривается как множество заключенных в нем вещественных чисел. Поставим
вопросы:
,…, каждый из которых
рассматривается как множество заключенных в нем вещественных чисел. Поставим
вопросы:
1) можно ли ввести отношения на множестве интервальных чисел, аналогичные отношениям на множестве вещественных чисел (>, <, =, ≠ и т. д.), так, чтобы они сохранили основные свойства соответствующих отношений между вещественными числами и имели содержательный смысл для интервальных чисел, позволяя решать прикладные задачи в интервальной постановке?
2) какие свойства отношений между вещественными числами сохраняются при их перенесении на интервальные числа?
3) что такое максимальное и минимальное интервальное число и как их найти, каковы условия максимальности (минимальности) интервала?
4) можно ли ввести полные системы отношений на множестве интервальных чисел, в которых каждая пара интервальных чисел обязательно находилась бы в одном из отношений данной системы?
5) какие полные системы отношений существуют?
В качестве математического аппарата при сравнении вещественных и
интервальных чисел и выборе экстремального числа используем непрерывную логику
(НЛ) в ее детерминированном [13, 14] и интервальном [15] вариантах. Для любой
пары (a, b)
вещественных чисел операции дизъюнкции ![]() и конъюнкции
и конъюнкции ![]() НЛ вводятся в
виде [13, 14]
НЛ вводятся в
виде [13, 14]
![]() (1)
(1)
Эти операции подчиняются законам тавтологии, переместительному,
сочетательному, распределительному одна относительно другой, поглощения и
распределительному закону относительно сложения. Для любой пары интервальных
чисел ![]() дизъюнкция
и конъюнкция НЛ вводятся через варианты этих операций (1) в виде следующих
теоретико-множественных конструкций
дизъюнкция
и конъюнкция НЛ вводятся через варианты этих операций (1) в виде следующих
теоретико-множественных конструкций
 (2)
(2)
Операции (2) подчиняются тем же законам, что и соответствующие операции (1) для вещественных чисел. Их результаты вычисляются по очевидным формулам [16]
 (3)
(3)
Отношения >, < между вещественными числами определим следующим образом:
![]() (4)
(4)
т. е. первое число больше (меньше) второго, только если их дизъюнкция НЛ равна первому (второму) числу, конъюнкция НЛ равна второму (первому) числу, а сами числа не равны. Отношения >, < между двумя числами накладывают на числа следующее ограничение (согласованность): если одно из чисел большее, то другое меньшее и обратно. Отношение = между интервальными числами в соответствии с теорией множеств справедливо только для интервальных чисел с совпадающим началом и концом.
Определения: 1) для данных множества М и совокупности R = (R1..., Rn) определенных на нем бинарных отношений Ri два элемента (mi mj) из M называются сравнимыми, если для некоторого Rk справедливо mi Rk mj или mj Rk mi, в противном случае эти элементы называются несравнимыми; 2) совокупность отношений R = (R1, ..., Rn) на множестве М, называется полной, если любые два элемента (mi, mj) из M сравнимы; в противном случае R называется неполной; 3) полная совокупность отношений R на множестве М называется разделительной, если любые два элемента (mi, mj) из М сравнимы только по одному из этих отношений.
2. Отношения взаиморасположения интервалов
Выделим пять элементарных отношений взаиморасположения интервальных
чисел: совпадение (C), сдвиг двусторонний (СД) или
односторонний справа (СП) или слева (СП) и накрытие (Н). Эти отношения для любых
двух интервалов ![]() определяются в виде следующих
условий для границ интервалов (символами -1 помечены соответствующие
обратные отношения):
определяются в виде следующих
условий для границ интервалов (символами -1 помечены соответствующие
обратные отношения):
![]() (5)
(5)
 (6)
(6)
 (7)
(7)
![]()
 (8)
(8)
![]() (9)
(9)
Названия введенных отношений соответствуют взаиморасположению сравниваемых интервалов на числовой оси. Это расположение всегда однозначно, что соответствует элементарности отношений (5)—(9).
1. Объединив отношения одностороннего сдвига справа (СП) и слева (СЛ), получим общее отношение одностороннего сдвига (СО):
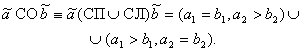 (10)
(10)
Как видно из (10), отношению СО соответствует объединение условий для границ интервалов в двух элементарных отношениях СП и СЛ, т. е. отношение СО уже не элементарное, а составное, ему соответствует двузначное взаиморасположение сравниваемых интервалов.
2. Объединив отношения двустороннего СД и одностороннего СО сдвигов, получим общее отношение сдвига Сд:
 (11)
(11)
Согласно (11) отношению Сд соответствует объединение условий для границ интервалов в трех элементарных отношениях: СД, СП и СЛ. Таким образом, отношение сдвига Сд — составное, ему соответствует трехзначное взаиморасположение сравниваемых интервалов. Условия для границ интервалов в (11) можно упростить по закону дистрибутивности алгебры множеств
 (12)
(12)
Практически удобна иная, чем (12), симметрическая форма условий. Она получается, если к правой части (11) добавить еще одну первую скобку (по закону идемпотентности алгебры множеств), а затем объединить одну первую скобку со второй, а другую — с третьей, применив к каждой паре скобок закон дистрибутивности. В итоге получим
![]() (13)
(13)
Согласно (13) интервал ![]() находится в отношении сдвига Сд
относительно интервала
находится в отношении сдвига Сд
относительно интервала ![]() , только если хотя бы одна из двух
границ
, только если хотя бы одна из двух
границ ![]() сдвинута
вправо относительно одноименной границы
сдвинута
вправо относительно одноименной границы ![]() (другая граница
(другая граница ![]() может быть
сдвинута вправо или совпадать с одноименной границей
может быть
сдвинута вправо или совпадать с одноименной границей ![]() ).
).
3. Объединяя отношения двустороннего сдвига СД и совпадения С, получаем составное отношение нестрогого двустороннего сдвига СДН:
 (14)
(14)
Согласно (14) отношению СДН соответствует объединение условий для границ интервалов в двух элементарных отношениях СД и С, что дает двузначное взаиморасположение сравниваемых интервалов.
4. Объединяя отношения одностороннего сдвига справа СП и совпадения С, получаем составное отношение нестрогого одностороннего сдвига справа СПН:
 (15)
(15)
Согласно (15) отношению СПН соответствует объединение условий для границ интервалов в двух элементарных отношениях СП и С, что означает двузначное взаиморасположение сравниваемых интервалов. Условия в (15) можно записать по закону дистрибутивности алгебры множеств в виде
![]() (16)
(16)
5. Объединив односторонний сдвиг слева СЛ и совпадение С, получим составное отношение нестрогого одностороннего сдвига слева СЛН:
 (17)
(17)
Отношению СЛН, согласно (17), соответствует объединение условий для границ интервалов в двух элементарных отношениях СЛ и С, т. е. взаиморасположение сравниваемых интервалов здесь двузначное. Условия в (17) можно, как и выше, упростить:
![]() (18)
(18)
6. Объединив отношения общего одностороннего сдвига СО (10) и совпадения С, получим составное отношение нестрогого общего одностороннего сдвига СОН с такими условиями для границ интервалов:
 (19)
(19)
Согласно (19) отношению СОН соответствует объединение условий в трех элементарных отношениях: СП, СЛ и С, что показывает трехзначное взаиморасположение сравниваемых интервалов. Условия в (19) можно упростить, добавив в правую часть еще одну третью скобку, объединив одну такую скобку с первой, а другую — со второй скобками и применив закон дистрибутивности алгебры множеств:
![]() (20)
(20)
7. Объединяя общий сдвиг Сд (11) и совпадение С, получим составное отношение нестрогого общего сдвига СдН:
 (21)
(21)
Отношению СдН соответствует объединение условий в четырех элементарных отношениях: СД, СП, СЛ и С, т. е. четырехзначное взаиморасположение сравниваемых интервалов. Условия в (21) можно упростить, применив закон дистрибутивности алгебры множеств к объединению первой скобки со второй и третьей скобки с четвертой, а затем — к объединению полученных результатов:
![]() (22)
(22)
Для получения составных отношений взаиморасположения интервальных чисел, кроме операции объединения элементарных отношений (5)—(9), можно использовать также операцию дополнения.
3. Свойства отношений взаиморасположения интервалов
Согласно определениям п. 1 полнота системы бинарных отношений R = (R1,..., Rn) на множестве М записывается в виде
![]() (23)
(23)
а признак разделительности этой системы — в виде
 (24)
(24)
Здесь U — достоверное, а ![]() — невозможное
событие. Очевидно, что совокупность элементарных отношений взаиморасположения
интервалов (5)— (9) полна. Эти отношения не пересекаются. Поэтому совокупность
элементарных отношений (5)—(9) — полная разделительная. Разбив множество
отношений (5)—(9) на непересекающиеся подмножества и образовав объединение
отношений каждого подмножества, получим новую полную разделительную
совокупность отношений. Этим путем в п. 2 были построены новые, составные
отношения взаиморасположения интервалов. Таким образом, имеем следующие полные
разделительные совокупности отношений взаиморасположения интервальных чисел:
— невозможное
событие. Очевидно, что совокупность элементарных отношений взаиморасположения
интервалов (5)— (9) полна. Эти отношения не пересекаются. Поэтому совокупность
элементарных отношений (5)—(9) — полная разделительная. Разбив множество
отношений (5)—(9) на непересекающиеся подмножества и образовав объединение
отношений каждого подмножества, получим новую полную разделительную
совокупность отношений. Этим путем в п. 2 были построены новые, составные
отношения взаиморасположения интервалов. Таким образом, имеем следующие полные
разделительные совокупности отношений взаиморасположения интервальных чисел:
{С, СД, СП, СЛ, Н}, {С, СД, СО, Н}, {СДН, СП, СЛ, Н},
{СПН, СД, СЛ, Н}, {СЛН, СД, СП, Н}, {С, Сд, Н},
{СОН, СД, Н}, {СдН, Н}. (25)
Первая совокупность (25) содержит только элементарные отношения взаиморасположения интервалов, последующие совокупности содержат также и составные отношения, благодаря чему общее число отношений в них меньше. Во всех совокупностях (25) имеется минимальное число отношений, так что исключение любого отношения приводит к потере ею свойства полноты. Любую совокупность (25) можно дополнить новыми отношениями, при этом совокупность становится неминимальной и может потерять свойство разделительности.
Установим свойства отношений взаиморасположения интервалов (подобные свойствам аналогичных отношений между вещественными числами), исходя из условий для границ интервалов. Напомним общие свойства отношений:
![]() (рефлексивность);
(26)
(рефлексивность);
(26)
![]() (симметричность); (27)
(симметричность); (27)
![]() (транзитивность); (28)
(транзитивность); (28)
![]() (антирефлексивность); (29)
(антирефлексивность); (29)
![]() (асимметричность); (30)
(асимметричность); (30)
![]() (антисимметричность). (31)
(антисимметричность). (31)
Сравнив определения отношений взаиморасположения интервалов (п. 2) с определениями свойств (26)—(30), находим свойства отношений (табл. 1). Известно, что отношения вещественных чисел обладают следующими свойствами:
· равенство чисел (a = b) — рефлексивностью, симметричностью, транзитивностью и антисимметричностью;
· строгое неравенство чисел (a > b) — транзитивностью, антирефлексивностью и асимметричностью;
·
нестрогое неравенство чисел ![]() — рефлексивностью,
транзитивностью и антисимметричностью.
— рефлексивностью,
транзитивностью и антисимметричностью.
Таблица 1
|
|
|
Свойства |
|||||
|
№ п/п |
Отношения взаиморасположения интервалов |
|
|
|
|
|
|
|
1 |
Совпадение (С) |
+ |
+ |
+ |
|
|
+ |
|
2 |
Двусторонний сдвиг(СД, СД0) |
|
|
+ |
+ |
+ |
|
|
3 |
Односторонний сдвиг справа (СП, СП0) |
|
|
+ |
+ |
+ |
|
|
4 |
Односторонний сдви слева (СЛ, СЛ0) |
|
|
+ |
+ |
+ |
|
|
5 |
Накрытие (Н, Н0) |
|
|
+ |
+ |
+ |
|
|
6 |
Односторонний сдвиг (СО) |
|
|
+ |
+ |
+ |
|
|
7 |
Общий сдвиг (Сд) |
|
|
+ |
+ |
+ |
|
|
8 |
Нестрогий двусторонний сдвиг (СДН) |
+ |
|
+ |
|
|
+ |
|
9 |
Нестрогий2 односторонний сдвиг справа (СПН) |
+ |
|
+ |
|
|
+ |
|
10 |
Нестрогий односторонний сдвиг слева (СЛН) |
+ |
|
+ |
|
|
+ |
|
11 |
Нестрогий односторонний сдвиг (СОН) |
+ |
|
+ |
|
|
+ |
|
12 |
Нестрогий общий сдвиг (СдН) |
+ |
|
+ |
|
|
+ |
Сравнив эти данные с табл. 1, видим, что по своим свойствам отношение совпадения интервалов (С) аналогично отношению равенства чисел, отношения строгого сдвига интервалов (СД, СП, СЛ, СО, Сд) и их накрытия (Н) аналогичны отношению строгого неравенства чисел, а отношения нестрогого сдвига интервалов (СДН, СПН, СЛН, СОН, СдН) — отношению нестрогого неравенства чисел.
4. Отношения интервальных чисел "равно", "не равно", "больше", "меньше", "несравнимо"
Введем отношения интервальных чисел. При построении этих отношений используем отношения взаиморасположения интервалов.
Начнем с отношений равенствами неравенства интервальных чисел ![]() . За основу
возьмем отношение С совпадения интервалов. Оно обладает всеми свойствами
отношения равенства чисел (п. 3) и содержит два интервала, которые состоят из
одних и тех же элементов, т. е. по теории множеств являются равными
множествами. Поэтому совпадающие интервалы будем считать равными интервальными
числами, т. е.
. За основу
возьмем отношение С совпадения интервалов. Оно обладает всеми свойствами
отношения равенства чисел (п. 3) и содержит два интервала, которые состоят из
одних и тех же элементов, т. е. по теории множеств являются равными
множествами. Поэтому совпадающие интервалы будем считать равными интервальными
числами, т. е.
![]() (32)
(32)
Из (32) следует условие неравенства интервальных чисел
![]() (33)
(33)
Отношения "больше" (> ) и "меньше" (< ) для интервальных чисел, согласно п. 3, следует искать среди отношений взаиморасположения интервалов — строгого сдвига СД, СП, СЛ, СО, Сд либо накрытия Н. Примем следующий принцип, обобщающий соответствующий принцип для вещественных чисел (4) на интервальные числа:
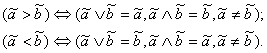 (34)
(34)
Здесь ![]() и
и
![]() —
операции (2) дизъюнкции и конъюнкции НЛ для интервалов. Как и в случае
вещественных чисел, этот принцип требует от интервальных чисел, находящихся в
отношениях >, <, согласованности: если одно из интервальных чисел
большее, то другое меньшее и обратно. Как показывает теорема 1, интервальные
числа всегда согласованы, что и делает возможным применение принципа (34).
—
операции (2) дизъюнкции и конъюнкции НЛ для интервалов. Как и в случае
вещественных чисел, этот принцип требует от интервальных чисел, находящихся в
отношениях >, <, согласованности: если одно из интервальных чисел
большее, то другое меньшее и обратно. Как показывает теорема 1, интервальные
числа всегда согласованы, что и делает возможным применение принципа (34).
Теорема 1. Для любой пары интервальных чисел ![]() верна эквивалентность
(согласованность интервальных чисел):
верна эквивалентность
(согласованность интервальных чисел):
![]() (35)
(35)
Доказательство. Докажем, что из левой части (35) следует правая часть.
Учитывая формулы (3) и (32), найдем

что и требовалось доказать. Доказательство того, что из правой части (35) следует левая часть, аналогично.
Назовем любые
два интервальных числа ![]() сравнимыми (несравнимыми) по
отношениям >, <, если они находятся (не находятся) в одном из отношений
>, < согласно (34).
сравнимыми (несравнимыми) по
отношениям >, <, если они находятся (не находятся) в одном из отношений
>, < согласно (34).
Теорема 2. Для того чтобы два интервальных числа ![]() были сравнимы
по отношениям >, < и в отношении
были сравнимы
по отношениям >, < и в отношении ![]() согласно (34), необходимо и
достаточно выполнения систем неравенств
согласно (34), необходимо и
достаточно выполнения систем неравенств ![]() или
или ![]() , а для того чтобы они
были несравнимы по отношениям >, < — выполнения систем неравенств
, а для того чтобы они
были несравнимы по отношениям >, < — выполнения систем неравенств ![]() .
.
Доказательство. Докажем достаточность условия неравенства ![]() . Возьмем его
первую систему неравенств (проверка достаточности для второй системы
аналогична). По определениям (33), (34) неравенства интервальных чисел и с
учетом формул (3) получаем такие следствия взятого условия:
. Возьмем его
первую систему неравенств (проверка достаточности для второй системы
аналогична). По определениям (33), (34) неравенства интервальных чисел и с
учетом формул (3) получаем такие следствия взятого условия:

что доказывает
достаточность условия. Необходимость условия неравенства ![]() , а также необходимость
и достаточность условия несравнимости по отношениям >, < доказываются
аналогично.
, а также необходимость
и достаточность условия несравнимости по отношениям >, < доказываются
аналогично.
Теорема 3. Для того чтобы два интервальных числа ![]() были сравнимы
по отношениям >, < и в отношении
были сравнимы
по отношениям >, < и в отношении ![]() согласно (34), необходимо и
достаточно выполнения систем неравенств
согласно (34), необходимо и
достаточно выполнения систем неравенств ![]() или
или ![]() . Доказательство следует
из того, что отношение
. Доказательство следует
из того, что отношение ![]() согласно (34) эквивалентно
отношению
согласно (34) эквивалентно
отношению ![]() ,
условие которого дает теорема 2.
,
условие которого дает теорема 2.
Если сравнить условия неравенства интервальных чисел >, < и их
несравнимости ![]() , устанавливаемые в теоремах 2, 3,
с условиями, при которых имеет место то или иное взаиморасположение интервалов
(п. 2), то придем к следующим выводам:
, устанавливаемые в теоремах 2, 3,
с условиями, при которых имеет место то или иное взаиморасположение интервалов
(п. 2), то придем к следующим выводам:
·
сравнимы по отношениям неравенств величин > и < только те
интервальные числа, которые находятся между собой в отношении общего сдвига Сд
= СД ![]() СП
СП
![]() СЛ,
причем сдвинутый вправо (влево) интервал является большим (меньшим), т. е.
СЛ,
причем сдвинутый вправо (влево) интервал является большим (меньшим), т. е.
 (36)
(36)
· несравнимы по отношениям неравенств > и < только те интервальные числа, которые находятся в отношении накрытия или совпадения:
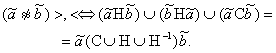 (37)
(37)
5. Отношения интервальных чисел "не больше", "не меньше", "больше или равно", "меньше или равно", "не равно"
Отношения интервальных чисел "не больше" ![]() , "не меньше"
, "не меньше" ![]() , "не
равно" (≠), "больше или равно"
, "не
равно" (≠), "больше или равно" ![]() , "меньше или
равно"
, "меньше или
равно" ![]() вводятся
так:
вводятся
так:
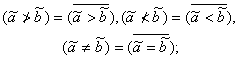 (38)
(38)
Здесь ![]() означает
отрицание A.
означает
отрицание A.
Из соотношений (38), используя полученные ранее условия нахождения
интервальных чисел в отношениях >, <, =, получаем условия, при которых эти
числа находятся в отношениях ![]() .
.
Теорема 4. Для того чтобы интервальные числа ![]() были в отношении
были в отношении ![]() согласно (38),
необходимо и достаточно выполнения систем неравенств
согласно (38),
необходимо и достаточно выполнения систем неравенств ![]() .
.
Доказательство. Согласно (38), для того чтобы ![]() и
и ![]() находились в отношении
находились в отношении ![]() , необходимо и
достаточно выполнение условия
, необходимо и
достаточно выполнение условия ![]() = НЕ А, где A — условие отношения
= НЕ А, где A — условие отношения ![]() . С учетом условия A из теоремы 2 имеем
. С учетом условия A из теоремы 2 имеем
![]()
или после применения законов де Моргана и распределительного алгебры множеств

Согласно закону поглощения алгебры множеств третья скобка последнего выражения поглощается четвертой. Кроме того, разложив вторую скобку
![]()
видим, что первая (третья) скобка этого разложения поглощается первой (четвертой) скобкой выражения A. В результате получаем
![]()
что и требовалось доказать.
Сравнив условие отношения интервальных чисел ![]() из теоремы 4 с
условиями различного взаиморасположения интервалов (п. 2), видим, что это
отношение верно только в следующих случаях:
из теоремы 4 с
условиями различного взаиморасположения интервалов (п. 2), видим, что это
отношение верно только в следующих случаях:
·
![]() находится в отношении
двустороннего сдвига СД к
находится в отношении
двустороннего сдвига СД к ![]() ;
;
·
![]() находится в отношении
одностороннего сдвига слева СЛ или справа СП к
находится в отношении
одностороннего сдвига слева СЛ или справа СП к ![]() ;
;
·
![]() накрывает
накрывает ![]() или
или ![]() накрывает
накрывает ![]() ,
,
·
![]() и
и ![]() совпадают, т. е.
совпадают, т. е.
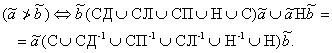 (39)
(39)
Учитывая (36), (37), правую часть (39) можно переписать:
![]() (40)
(40)
т. е.
отношение ![]() означает,
что
означает,
что ![]() <
<
![]() либо
либо
![]() несравнимо
с
несравнимо
с ![]() по
отношениям >, <. Видим существенное отличие интервальных чисел от
вещественных, где
по
отношениям >, <. Видим существенное отличие интервальных чисел от
вещественных, где ![]() означает только a ≤ b,
а несравнимость a и b
невозможна.
означает только a ≤ b,
а несравнимость a и b
невозможна.
Теорема 5. Для того чтобы интервальные числа ![]() = [a1,
a1] и
= [a1,
a1] и ![]() = [b1,
b2] были в отношении
= [b1,
b2] были в отношении ![]() согласно (38),
необходимо и достаточно выполнения систем неравенств
согласно (38),
необходимо и достаточно выполнения систем неравенств ![]() .
.
Доказательство. Согласно (34) отношение ![]() <
< ![]() эквивалентно
отношению
эквивалентно
отношению ![]() >
>
![]() .
Отсюда с учетом определений (38) находим
.
Отсюда с учетом определений (38) находим ![]() и для получения нужного условия
отношения
и для получения нужного условия
отношения ![]() остается
взять условие отношения
остается
взять условие отношения ![]() >
> ![]() , содержащееся в теореме
4:
, содержащееся в теореме
4:
![]()
Как и для теоремы 4, устанавливаем, что отношение интервальных чисел ![]() справедливо
только в следующих случаях:
справедливо
только в следующих случаях:
·
![]() находится в отношении
двустороннего сдвига СД к
находится в отношении
двустороннего сдвига СД к ![]()
·
![]() находится в отношении
одностороннего сдвига слева СЛ или справа СП к
находится в отношении
одностороннего сдвига слева СЛ или справа СП к ![]() ;
;
·
![]() накрывает
накрывает ![]() или
или ![]() накрывает
накрывает ![]() ;
;
·
![]() и
и ![]() совпадают, т. е.
совпадают, т. е.
 (41)
(41)
Соотношение (41) с учетом (36), (37) можно переписать в виде
![]() (42)
(42)
т. е.
отношение ![]() означает:
означает:
![]() >
>
![]() либо
либо
![]() несравнимо
с
несравнимо
с ![]() по
отношениям >, <. Опять видим существенное отличие интервальных чисел от
вещественных, где
по
отношениям >, <. Опять видим существенное отличие интервальных чисел от
вещественных, где ![]() означает a ≥ b.
означает a ≥ b.
Теорема 6. Для того чтобы интервальные числа ![]() = [a1,
a1] и
= [a1,
a1] и ![]() = [b1,
b2] были в отношении
= [b1,
b2] были в отношении ![]() ≥
≥ ![]() согласно (38),
необходимо и достаточно выполнения систем неравенств
согласно (38),
необходимо и достаточно выполнения систем неравенств ![]() , т. е.
, т. е. ![]() .
.
Доказательство получается из определения (38) отношения ![]() ≥
≥ ![]() , согласно
которому для получения искомого условия следует взять объединение условий
отношений
, согласно
которому для получения искомого условия следует взять объединение условий
отношений ![]() ≥
≥
![]() и
и ![]() =
= ![]() из теоремы 2 и
формулы (32).
из теоремы 2 и
формулы (32).
Теорема 7. Для того чтобы интервальные числа ![]() = [a1,
a1] и
= [a1,
a1] и ![]() = [b1,
b2] были в отношении
= [b1,
b2] были в отношении ![]() ≤
≤ ![]() согласно (38),
необходимо и достаточно выполнение систем неравенств
согласно (38),
необходимо и достаточно выполнение систем неравенств ![]() , т. е. (a1 ≥ b1,
a2 ≥ b2).
, т. е. (a1 ≥ b1,
a2 ≥ b2).
Доказательство проводится аналогично доказательству теоремы 6.
Согласно (38) отношение интервальных чисел ![]() ≥
≥ ![]() есть объединение
отношений
есть объединение
отношений ![]() >
>
![]() и
и ![]() =
= ![]() . Поэтому
взаиморасположение интервалов, находящихся в отношении ≥, есть
объединение взаиморасположения интервалов с отношениями > и =. Последние
даны в (32), (36). В итоге получаем
. Поэтому
взаиморасположение интервалов, находящихся в отношении ≥, есть
объединение взаиморасположения интервалов с отношениями > и =. Последние
даны в (32), (36). В итоге получаем
![]() (43)
(43)
Аналогично анализируется отношение интервальных чисел ![]() ≤
≤ ![]() , что дает
, что дает
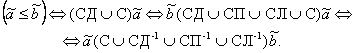 (44)
(44)
Назовем любые два интервальных числа ![]() = [a1,
a2] и
= [a1,
a2] и ![]() = [b1,
b2] сравнимыми (несравнимыми) по
отношениям ≥, ≤ , если они находятся (не находятся) в одном из
отношений ≥, ≤ согласно (38).
= [b1,
b2] сравнимыми (несравнимыми) по
отношениям ≥, ≤ , если они находятся (не находятся) в одном из
отношений ≥, ≤ согласно (38).
Как показывают соотношения (43), (44) (с учетом того, что в их правых частях фигурируют все элементарные отношения взаиморасположения интервалов (5)—(9), кроме накрытия Н):
·
сравнимы по отношениям ≥ и ≤ только те интервальные
числа, которые находятся в отношении общего сдвига Сд = СД ![]() СП
СП ![]() СЛ или совпадения С,
причем сдвинутый вправо (влево) интервал является строго большим (строго
меньшим), согласно (36), а совпадающие интервалы равны, согласно (32);
СЛ или совпадения С,
причем сдвинутый вправо (влево) интервал является строго большим (строго
меньшим), согласно (36), а совпадающие интервалы равны, согласно (32);
· несравнимы по отношениям ≥ и ≤ только те интервальные числа, которые находятся в отношении накрытия Н, т. е.
![]() (45)
(45)
Теорема 8. Для того чтобы интервальные числа ![]() и
и ![]() были в
отношении ≥ и ≤, необходимо и достаточно выполнения систем
неравенств (a1 < b1, a2
> b2)
были в
отношении ≥ и ≤, необходимо и достаточно выполнения систем
неравенств (a1 < b1, a2
> b2) ![]() (b1
< a1, b2
> a2).
(b1
< a1, b2
> a2).
Доказательство следует из эквивалентности (45), так как отношениям Н и H-1 соответствуют первая и вторая системы неравенств.
Сопоставление (45) с (37) показывает, что если сравнивать интервальные числа как с помощью отношений >, <, так и с помощью отношения = (т. е. расширить операции сравнения от строгих >, < до нестрогих неравенств ≥ и ≤), то множество несравнимых интервальных чисел сузится до множества интервалов, находящихся в отношении накрытия.
Теорема 9. Для того чтобы интервальные числа ![]() и
и ![]() были в
отношении
были в
отношении ![]() согласно
(38), необходимо и достаточно выполнения систем неравенств
согласно
(38), необходимо и достаточно выполнения систем неравенств ![]() .
.
Доказательство следует из определений (32) равенства ![]() =
= ![]() и (38)
неравенства
и (38)
неравенства ![]() как
отрицания равенства.
как
отрицания равенства.
Как и в теоремах 4, 5 находим, что отношение ![]() интервальных чисел
верно только если:
интервальных чисел
верно только если:
·
![]() в отношении двустороннего сдвига
СД к
в отношении двустороннего сдвига
СД к ![]() либо
наоборот;
либо
наоборот;
·
![]() в отношении одностороннего сдвига
слева СЛ или справа СП к
в отношении одностороннего сдвига
слева СЛ или справа СП к ![]() либо наоборот;
либо наоборот;
·
![]() накрывает
накрывает ![]() либо наоборот, т. е.
либо наоборот, т. е.
 (46)
(46)
6. Свойства отношений интервальных чисел
Определим наборы отношений интервальных чисел, являющиеся полными и/или разделительными; каждого из них достаточно для решения всех теоретических и прикладных задач, связанных со сравнением интервальных чисел. Мы знаем, что набор (5)—(9) из пяти элементарных отношений взаиморасположения интервалов — полный разделительный. Но любое отношение интервальных чисел эквивалентно объединению некоторого числа элементарных отношений взаиморасположения интервалов [формулы (32), (36), (37), (39), (41)—(46)]. Так что полным разделительным набором отношений интервальных чисел является только тот набор, в котором:
· выражения всех этих отношений в виде объединения элементарных отношений взаиморасположения интервалов в совокупности содержит все пять названных элементарных отношений;
· выражения любых двух отношений не содержат общих элементарных отношений.
На основе этого, перебрав все комбинации введенных отношений интервальных чисел, получаем все полные разделительные наборы этих отношений. Перебор удобно осуществлять с помощью таблицы включений (табл. 2), в которой строки помечены элементарными отношениями взаиморасположения интервалов, а столбцы — отношениями интервальных чисел, причем пометка в (i j)-й клетке таблицы означает, что выражение отношения интервальных чисел j содержит элементарное отношение взаиморасположения интервалов i. Ясно, что каждое покрытие строк табл. 2 ее непересекающимися (т. е. не имеющими общих пометок в одних и тех же строках) столбцами и только оно дает один полный разделительный набор. В итоге получаем следующие полные разделительные наборы отношений интервальных чисел:
 (47)
(47)
Ясно также, что каждое покрытие строк табл. 2 ее пересекающимися столбцами дает один полный неразделительный набор. Отсюда имеем следующие полные неразделительные наборы отношений интервальных чисел:
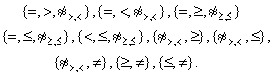 (48)
(48)
Таблица 2
|
|
|
Отношения интервальных чисел |
|
||||||||||||
|
№ п/п |
Элементарные отношения взаиморасположения интервалов |
= |
> |
< |
|
|
|
≥ |
≤ |
|
|
|||
|
1 |
С |
+ |
|
|
+ |
+ |
+ |
+ |
+ |
|
|
|||
|
2 |
СД |
|
+ |
+ |
|
+ |
+ |
+ |
+ |
|
+ |
|||
|
3 |
СП |
|
+ |
+ |
|
+ |
+ |
+ |
+ |
|
+ |
|||
|
4 |
СЛ |
|
+ |
+ |
|
+ |
+ |
+ |
+ |
|
+ |
|||
|
5 |
Н |
|
|
|
+ |
+ |
+ |
|
|
+ |
+ |
|||
Определим наличие отношений интервальных чисел свойств рефлексивности,
симметричности, транзитивности, антирефлексивности, антисимметричности,
асимметричности. Мы знаем, что любое отношение интервальных чисел R есть объединение нескольких элементарных отношений
взаиморасположения интервалов Ri.
Поэтому множество A свойств каждого отношения R интервальных чисел есть пересечение множеств свойств,
входящих в R элементарных отношений Ri с тремя поправками. Во-первых, из А
надо исключить те свойства отношений Ri,
которые исчезают в результате взаимодействия пар элементарных отношений (Ri, Rj),
обладающих данным свойством по отдельности, но не в объединении ![]() ; в нашем
случае это пары элементарных отношений (Н, H-1),
(СД, СД-1), (СП, СП-1), (СЛ, СЛ-1), а
свойства, которые они теряют при объединении — транзитивность и
асимметричность. Во-вторых, в А надо включить те свойства отношений R, которые сохраняются в объединении пар элементарных
отношений
; в нашем
случае это пары элементарных отношений (Н, H-1),
(СД, СД-1), (СП, СП-1), (СЛ, СЛ-1), а
свойства, которые они теряют при объединении — транзитивность и
асимметричность. Во-вторых, в А надо включить те свойства отношений R, которые сохраняются в объединении пар элементарных
отношений ![]() благодаря
одному из отношений Ri (второе отношение Rj
этим свойством не обладает); в нашем случае это пары элементарных отношений (С,
СД), (С, СП), (С, СЛ), (С, Н), (С, СД-1), (С, СП-1), (С,
СЛ-1), (С, Н-1), а сохраняемые свойства отношения С —
рефлексивность и антисимметричность. В-третьих, в A
надо включить свойства отношений R, которые
появляются в результате объединения пар (Ri,
Rj) элементарных отношений и которыми
последние не обладают по отдельности. В нашем случае это пары (Н, Н-1),
(СД, СД-1), (СП, СП-1), (СЛ, СЛ-1), а
появляющееся свойство — симметричность. Используя выражения отношений R в виде объединения элементарных отношений Rj [формулы (32), (36), (37), (39), (41)—(46)]
и перечень свойств элементарных отношений Rj
(см. табл. 1, № 1—5), получим перечень свойств отношений интервальных чисел
(табл. 3). В табл. 3 указаны соответствующие свойства интервальных чисел.
благодаря
одному из отношений Ri (второе отношение Rj
этим свойством не обладает); в нашем случае это пары элементарных отношений (С,
СД), (С, СП), (С, СЛ), (С, Н), (С, СД-1), (С, СП-1), (С,
СЛ-1), (С, Н-1), а сохраняемые свойства отношения С —
рефлексивность и антисимметричность. В-третьих, в A
надо включить свойства отношений R, которые
появляются в результате объединения пар (Ri,
Rj) элементарных отношений и которыми
последние не обладают по отдельности. В нашем случае это пары (Н, Н-1),
(СД, СД-1), (СП, СП-1), (СЛ, СЛ-1), а
появляющееся свойство — симметричность. Используя выражения отношений R в виде объединения элементарных отношений Rj [формулы (32), (36), (37), (39), (41)—(46)]
и перечень свойств элементарных отношений Rj
(см. табл. 1, № 1—5), получим перечень свойств отношений интервальных чисел
(табл. 3). В табл. 3 указаны соответствующие свойства интервальных чисел.
Из сравнения свойств отношений вещественных чисел и интервальных чисел
(табл. 3) следует их почти полное совпадение (25 случаев из 28). Различие
имеется лишь для отношений ![]() , которые для вещественных чисел
транзитивны, а для интервальных чисел — нет. Причина различия в том, что
указанные отношения для интервальных чисел содержат в качестве составляющей
нетранзитивные отношения Н и Н-1 накрытия интервалов [см. формулы
(37), (39), (41)]. В случае же вещественных чисел этой составляющей нет.
, которые для вещественных чисел
транзитивны, а для интервальных чисел — нет. Причина различия в том, что
указанные отношения для интервальных чисел содержат в качестве составляющей
нетранзитивные отношения Н и Н-1 накрытия интервалов [см. формулы
(37), (39), (41)]. В случае же вещественных чисел этой составляющей нет.
Таблица 3
|
№ п/п |
Отношение величин интервалов |
Свойства |
|||||
|
|
|
|
|
|
|
||
|
1 |
Равно (=) |
+ • |
+ • |
+ • |
|
|
+ • |
|
2 |
Больше (>) |
|
|
+ • |
+ • |
+ • |
|
|
3 |
Меньше (<) |
|
|
+ • |
+ • |
+ • |
|
|
4 |
Несравнимо по отношениям >, < (≠ >, <) |
+ • |
+ • |
|
|
|
+ • |
|
5 |
Не
больше ( |
+ • |
|
• |
|
|
+ • |
|
6 |
Не
меньше ( |
+ • |
|
• |
|
|
+ • |
|
7 |
Больше или равно (≥) |
+ • |
|
+ • |
|
|
+ • |
|
8 |
Меньше или равно (≤) |
+ • |
|
+ • |
|
|
+ • |
|
9 |
Несравнимо по отношениям ≥ и ≤ (≠≥, ≤) |
|
+ |
|
+ |
|
+ |
|
10 |
Не равно (≠) |
|
+ • |
|
+ • |
|
|
|
Примечания: 1. Обозначение + в клетке i j показывает наличие свойства j у отношения интервалов i, а обозначение • в клетке ij – наличие свойства j у отношения чисел i. 2.
Отношение 9-е |
|||||||
7. Максимальные и минимальные интервальные числа
По необходимым и достаточным условиям того, что два интервальных числа
находятся в отношениях >, <, ≥, ≤ или несравнимы по этим
отношениям (теоремы 2, 3, 6—8), всегда можно выделить (строго или нестрого)
большее либо меньшее из двух чисел либо заключить, что они несравнимы.
Распространим эти результаты на общий случай произвольного количества
интервальных чисел ![]() . Назовем число
. Назовем число ![]() нестрого
(строго) максимальным среди чисел
нестрого
(строго) максимальным среди чисел ![]() , если оно сравнимо
, если оно сравнимо ![]() по отношениям ≥,
≤ (по отношениям >, <) и находится с ними в отношениях
по отношениям ≥,
≤ (по отношениям >, <) и находится с ними в отношениях ![]() (в отношениях
(в отношениях
![]() )-
Назовем число
)-
Назовем число ![]() нестрого (строго) минимальным
среди чисел
нестрого (строго) минимальным
среди чисел ![]() ,
если оно сравнимо с
,
если оно сравнимо с ![]() по отношениям ≥, ≤ (по
отношениям >, <) и находится с ними в отношениях
по отношениям ≥, ≤ (по
отношениям >, <) и находится с ними в отношениях ![]() (в отношениях
(в отношениях ![]() ). Из п. п. 1,
4, 5 следует, что нестрого максимальное интервальное число находится с другими
интервальными числами в отношении общего сдвига или совпадения
). Из п. п. 1,
4, 5 следует, что нестрого максимальное интервальное число находится с другими
интервальными числами в отношении общего сдвига или совпадения ![]() , а строго
максимальное — в отношении общего сдвига Сд = СД
, а строго
максимальное — в отношении общего сдвига Сд = СД ![]() СП
СП ![]() СЛ. Аналогично нестрого
минимальное интервальное число находится с другими интервальными числами в
отношении обратного общего сдвига или совпадения Сд-1
СЛ. Аналогично нестрого
минимальное интервальное число находится с другими интервальными числами в
отношении обратного общего сдвига или совпадения Сд-1 ![]() С = СД-1
С = СД-1
![]() СП-1
СП-1
![]() СЛ-1
СЛ-1
![]() С, а
строго минимальное — в отношении обратного общего сдвига Сд-1 = СД-1
С, а
строго минимальное — в отношении обратного общего сдвига Сд-1 = СД-1
![]() СП-1
СП-1
![]() СЛ-1.
СЛ-1.
Теорема 10. Для того чтобы в системе интервальных чисел ![]() число
число ![]() было нестрого
максимальным, необходимо и достаточно выполнения двух соотношений:
было нестрого
максимальным, необходимо и достаточно выполнения двух соотношений:
 (49)
(49)
а чтобы ![]() было нестрого
минимальным, необходимо и достаточно иметь
было нестрого
минимальным, необходимо и достаточно иметь
 (50)
(50)
Здесь ![]() и
и ![]() — операции
дизъюнкции и конъюнкции НЛ (1).
— операции
дизъюнкции и конъюнкции НЛ (1).
Доказательство. Докажем необходимость и достаточность условий (49)
максимума. Нестрогая максимальность ![]() означает, что
означает, что ![]() . Согласно
теореме 6 первое неравенство означает
. Согласно
теореме 6 первое неравенство означает ![]() ,..., последнее неравенство —
,..., последнее неравенство — ![]() ; достоверное
неравенство
; достоверное
неравенство ![]() означает
означает
![]() .
Соединив в этой цепочке пар неравенств все первые (вторые) неравенства, получим
первое (второе) равенство (49). Необходимость и достаточность условий (50)
минимума доказывается аналогично.
.
Соединив в этой цепочке пар неравенств все первые (вторые) неравенства, получим
первое (второе) равенство (49). Необходимость и достаточность условий (50)
минимума доказывается аналогично.
Теорема
11. Для того чтобы в системе интервальных чисел ![]() число
число ![]() было строго
максимальным, необходимо и достаточно выполнения системы соотношений
было строго
максимальным, необходимо и достаточно выполнения системы соотношений
 (51)
(51)
а чтобы а у было строго минимальным, необходимо и достаточно иметь
 (52)
(52)
Доказательство. Докажем необходимость и достаточность условий (51)
максимума. Строгая максимальность ![]() означает, что
означает, что ![]() . Согласно
теореме 2 первое неравенство означает
. Согласно
теореме 2 первое неравенство означает ![]()
![]() (a11
≠ a21 или a12
≠ a22), ..., последнее неравенство
—
(a11
≠ a21 или a12
≠ a22), ..., последнее неравенство
— ![]()
![]() (a11 ≠ ak1 или a12 ≠
ak2)'
достоверное неравенство
(a11 ≠ ak1 или a12 ≠
ak2)'
достоверное неравенство ![]() означает
означает ![]() . Соединив в этой
цепочке пар неравенств ≥ все первые (вторые) неравенства, получим первое
(второе) равенство (511), а соединив в ней все объединения пар
неравенств ≠, получим остальные соотношения (512). Необходимость
и достаточность условий (52) минимума доказывается аналогично.
. Соединив в этой
цепочке пар неравенств ≥ все первые (вторые) неравенства, получим первое
(второе) равенство (511), а соединив в ней все объединения пар
неравенств ≠, получим остальные соотношения (512). Необходимость
и достаточность условий (52) минимума доказывается аналогично.
Сравнив (51) и (52) с (49) и (50), видим, что условия строгой максимальности (51) или минимальности (52) интервального числа складываются из условия его нестрогой максимальности (511) или минимальности (521) и дополнительного условия того, что оно не равно остальным интервальным числам данной системы, т. е. строго больше их [условие (512)] или строго меньше [условие (522)].
Теоремы 10, 11 позволяют свести выбор экстремального интервального числа к выбору двух экстремальных вещественных чисел.
Алгоритм выделения нестрого максимального интервального числа
Шаг 1. Для имеющегося множества М интервальных чисел ![]() отыскиваем
максимальный элемент множества M1 = {a11, a21,…,
ak1} нижних границ всех
интервалов. В общем случае таких элементов может быть несколько, они образуют
некоторое подмножество М1’ множества M1.
отыскиваем
максимальный элемент множества M1 = {a11, a21,…,
ak1} нижних границ всех
интервалов. В общем случае таких элементов может быть несколько, они образуют
некоторое подмножество М1’ множества M1.
Шаг 2. Для того же множества М ищем максимальный элемент множества M2 = {a12, a22,…, ak2} верхних границ всех интервалов. Таких элементов может быть несколько, они образуют подмножество М2’ множества М2.
Шаг 3. Из подмножеств М1’ = {ai1} и М2’
= {ai2} выбираются все
пары (ai1, ai2) с одинаковым значением первого
индекса i. Эти пары образуют интервальные числа ![]() и составляют
подмножество М' заданного множества
и составляют
подмножество М' заданного множества ![]() интервальных чисел.
Любое интервальное число
интервальных чисел.
Любое интервальное число ![]() есть искомое нестрого
максимальное число.
есть искомое нестрого
максимальное число.
Алгоритм выделения нестрого минимального интервального числа отличается от изложенного лишь тем, что на шагах 1 и 2 отыскивается не максимальные, а минимальные элементы множеств M1 и М2.
Как следует из приведенных алгоритмов, нестрого максимальное (минимальное) интервальное число существует не всегда. Для его существования необходимо и достаточно, чтобы множество М' было не пусто.
Алгоритм выделения строго максимального интервального числа
Этап 1. Выделение с помощью вышеизложенного трехшагового алгоритма
какого-то одного нестрогого максимального интервального числа ![]() ,
удовлетворяющего условию (511) нестрогой максимальности.
,
удовлетворяющего условию (511) нестрогой максимальности.
Этап 2. Проверка дополнительного условия (512) того,
что выделенное число ![]() строго больше остальных
интервальных чисел данной системы, т. е. является строго максимальным. Если (512)
выполнено, то конец процедуры. Если нет, то переход к этапу 1 с выделением
следующего нестрого максимального интервального числа и т. д.
строго больше остальных
интервальных чисел данной системы, т. е. является строго максимальным. Если (512)
выполнено, то конец процедуры. Если нет, то переход к этапу 1 с выделением
следующего нестрого максимального интервального числа и т. д.
Необходимость выполнения этапа 2 отпадает, если на этапе 1 выделять не
одно, а все т интервальных числа, удовлетворяющих условию (511) и
потому могущие считаться нестрого максимальными. При этом, если m = 1, то и без этапа 2 ясно, что выделенное на этапе 1
нестрого максимальное интервальное число ![]() на самом деле является строго
максимальной. Если m ≥
2, то ясно, что все выделенные на этапе 1 нестрого максимальные интервальные
числа, "подозрительные" на строгую оптимальность, на самом деле
таковыми не являются, т. е. строго максимальных интервальных чисел не
существует. Наконец, если m = 0, т. е. не
существуют нестрого максимальные интервальные числа, "подозрительные"
на строгую максимальность, то тем более не существуют строго максимальные
интервальные числа. Таким образом, строго максимальное интервальное число
существует, только если существует лишь одно нестрого максимальное интервальное
число, в этом случае первое равно второму. Строго максимальное интервальное
число, в отличие от нестрогого, всегда единственно.
на самом деле является строго
максимальной. Если m ≥
2, то ясно, что все выделенные на этапе 1 нестрого максимальные интервальные
числа, "подозрительные" на строгую оптимальность, на самом деле
таковыми не являются, т. е. строго максимальных интервальных чисел не
существует. Наконец, если m = 0, т. е. не
существуют нестрого максимальные интервальные числа, "подозрительные"
на строгую максимальность, то тем более не существуют строго максимальные
интервальные числа. Таким образом, строго максимальное интервальное число
существует, только если существует лишь одно нестрого максимальное интервальное
число, в этом случае первое равно второму. Строго максимальное интервальное
число, в отличие от нестрогого, всегда единственно.
Алгоритм выделения строго минимального интервального числа отличается от
изложенного содержанием этапа 1 [где выделяется нестрого минимальное
интервальное число с помощью условия (521)], этапа 2 [где идет
проверка того, что ![]() строго меньше остальных
интервальных чисел, с помощью условия (522)] и последующими
рассуждениями [где (511) заменяется на (522), а слово
"максимальный" на "минимальный"].
строго меньше остальных
интервальных чисел, с помощью условия (522)] и последующими
рассуждениями [где (511) заменяется на (522), а слово
"максимальный" на "минимальный"].
Итак, строго максимальное (минимальное) интервальное число существует не всегда, а лишь тогда, когда существует единственное нестрого максимальное (минимальное) интервальное число.
* * *
В настоящей статье введены отношения на множестве интервальных чисел,
аналогичные отношениям на множестве вещественных чисел (>, <, ![]() ), так что
первые сохраняют основные свойства вторых и в то же время имеют содержательный
смысл для интервальных чисел. Это открывает возможность строгого решения задач
оптимизации, управления, измерения и т. д., по неточно известным (интервальным)
параметрам систем. Такая постановка задач более реалистична, чем постановка с
точно известными параметрами. Однако не всякие интервальные числа сравнимы по
отношениям >,<,
), так что
первые сохраняют основные свойства вторых и в то же время имеют содержательный
смысл для интервальных чисел. Это открывает возможность строгого решения задач
оптимизации, управления, измерения и т. д., по неточно известным (интервальным)
параметрам систем. Такая постановка задач более реалистична, чем постановка с
точно известными параметрами. Однако не всякие интервальные числа сравнимы по
отношениям >,<, ![]() и не из всякой системы таких
чисел можно выделить максимальное (минимальное). Поэтому интервальные
постановки прикладных задач не всегда имеют решение. Для увеличения числа
разрешимых случаев можно применить два подхода: 1) сужение интервалов возможных
значений параметров изучаемых систем путем пополнения информации о системе; 2)
построение новых, более гибких систем отношений (сравнения) интервалов, в
которых любые интервальные числа (или хотя бы большее их число) оказываются
сравнимыми.
и не из всякой системы таких
чисел можно выделить максимальное (минимальное). Поэтому интервальные
постановки прикладных задач не всегда имеют решение. Для увеличения числа
разрешимых случаев можно применить два подхода: 1) сужение интервалов возможных
значений параметров изучаемых систем путем пополнения информации о системе; 2)
построение новых, более гибких систем отношений (сравнения) интервалов, в
которых любые интервальные числа (или хотя бы большее их число) оказываются
сравнимыми.
Список литературы
1. Алефельд Г., Херцбергер Ю. Введение в интервальные вычисления. М.: Мир. 1987.
2. Шокин Ю. И. Интервальный анализ. Новосибирск: Наука, 1981.
3. Калмыков С. А., Шокин Ю. И., Юлдашев 3. X. Методы интервального анализа. Новосибирск: Наука, 1986.
4. Вощинин А. П., Сотиров Г. Р. Оптимизация в условиях неопределенности. М. — София: Техника, 1989.
5. Левин В. И. О недетерминистской дискретной оптимизации // Принятие решений в условиях неопределенности. (Сб. трудов) Изд-во Уфимского авиационного ин-та, Уфа, 1990.
6. Allen J. F. Maintaining knowledge about temporal intervals. Communications of the ACM. 26 (1983). N 11. P. 832-843.
7. Allen J. F., Kautz H. A., Pelavin R. N., Tenenberg J. D. Reasoning about plans. Morgan Kaufmann, San Mateo, CA, 1991.
8. Shoham Y. Artificial intelligence techniques in Prolog. Morgan Kaufmann, San Francisco, CA, 1994.
9. Тимохин С. Г., Шапкин А. В. О задачах линейного программирования в условиях неточных данных // Экономика и математические методы, 17 (1981). № 5. С. 955—963.
10. Libura M. Integer programming problems with inexact objective function // Control and Cybern. 9 (1980). N 4. P. 189—202.
11.Семенова Н. В. Решение одной задачи обобщенного целочисленного программирования // Кибернетика, 1980. № 5. С. 25-31.
12. Рощин В. А., Семенова Н. В., Сергиенко И. В. Вопросы решения задач неточного целочисленного программирования // Кибернетика, 1989. № 2. С. 42—46.
13. Левин В. И. Структурно-логические методы исследования сложных систем с применением ЭВМ. М.: Наука, 1987.
14. Левин В. И. Непрерывная логика и ее применение // Информационные технологии, 1997. № 1. С. 17—21.
15. Левин В. И. Недетерминистская бесконечнозначная логика и ее применение // Логическое управление с использованием ЭВМ. Тез. докл. XII Всесоюзного симпозиума. 1989. С. 20-26.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 7, 1998
ИНТЕЛЛЕКТУАЛЬНЫЕ СИСТЕМЫ
Ключевые слова: Интервальные вычисления, оптимизация, непрерывная логика, отношения интервальных чисел.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



