научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2012
DOI: 10.7463/0113.0521994
УДК 681.5.015
Вычислительный центр им. А.А. Дородницына Российской академии наук
Российский университет дружбы народов
Введение
Структурно-параметрическая идентификация математических моделей может быть выполнена сегодня с использованием последних достижений в области информационных технологий.
В частности метод генетического программирования[1] и его развитие, метод грамматической эволюции [2] и метод аналитического программирования [3] могут быть использованы для получения математических моделей различных систем и процессов. К этому же классу методов относится метод сетевого оператора [4-6]. Различие между этими методами заключается в том, что с помощью метода сетевого оператора можно получить математические выражения, включающие только унарные и бинарные операции. Методы генетического программирования, грамматической эволюции и аналитического программирования предназначены для синтеза текста программ, поэтому они могут включать любые функции и операторы. С другой стороны, метод сетевого оператора при поиске структуры и параметров математического выражения использует базисную модель для данного выражения, которая может задаваться на основании опыта. Такой подход позволяет реализовать целенаправленный поиск оптимального решения в окрестности базисного, что существенно сокращает время поиска и пространство возможных решений.
В настоящей работе рассматривается задача идентификации математической модели химической реакции. Рассматриваемая задача актуальна, так как по модели химической реакции, варьировав в широком допустимом интервале значения исходных реагентов, катализаторов, а также условия проведения реакции (температура, давление и объем) можно прогнозировать максимум выхода целевых продуктов реакции за оптимальное время. Сочетание натурного химического и вычислительного эксперимента на основе использования технологий параллельных вычислений позволяет, с одной стороны сэкономит материальные и трудовые ресурсы, а с другой исследовать химические реакции в условиях, которые невозможно реализовать в химическом опыте. Для решения задачи идентификации в задаче использован метод сетевого оператора.
1. Постановка задачи
Рассмотрим задачу идентификации математической модели химической реакции.
Заданы результаты эксперимента по наблюдению изменения концентраций веществ, взаимодействующих во время химической реакции
![]() , (1)
, (1)
где ![]() - наблюдаемый в момент
- наблюдаемый в момент ![]() вектор показателей концентрации химической реакции,
вектор показателей концентрации химической реакции, ![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() ; (2)
; (2)
![]() ,
, ![]() - концентрация вещества
- концентрация вещества ![]() химической реакции,
химической реакции, ![]() - известные функции, описывающие значения показателя концентраций.
- известные функции, описывающие значения показателя концентраций.
Известно, что в химической реакции первоначально при детальном рассмотрении механизма реакции по стадиям ![]() . Остальные
. Остальные ![]() веществ получаются в результате реакции.
веществ получаются в результате реакции.
Для описания изменения концентраций веществ во времени определена система дифференциальных уравнения
![]() , (3)
, (3)
где ![]() ,
, ![]() .
.
Функции ![]() описывают закон изменения концентраций
описывают закон изменения концентраций ![]() ,
, ![]() при взаимодействии веществ
при взаимодействии веществ ![]() и
и ![]() :
:
![]() ,
, ![]() . (4)
. (4)
Здесь ![]() - неизвестный по величине постоянный параметр,
- неизвестный по величине постоянный параметр, ![]() .
.
Предполагаем, что структура функции ![]() и значения параметров
и значения параметров ![]() ,
, ![]() неизвестны.
неизвестны.
Заданы ограничения в виде алгебраических уравнений баланса
![]() ,
, ![]() . (5)
. (5)
Необходимо найти структуру функций (4) и параметры ![]() ,
, ![]() , чтобы в результате решения системы дифференциальных уравнений (3) для заданных начальных значений
, чтобы в результате решения системы дифференциальных уравнений (3) для заданных начальных значений
![]() , ¼,
, ¼, ![]() ,
, ![]() ,¼,
,¼,![]() (6)
(6)
минимизировать значение критерия
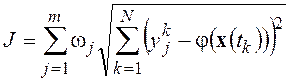 , (7)
, (7)
где ![]() - решение системы (3) в момент
- решение системы (3) в момент ![]() и удовлетворять уравнениям баланса (5)
и удовлетворять уравнениям баланса (5)
![]() ,
, ![]() , (8)
, (8)
![]() - весовые коэффициенты
- весовые коэффициенты
2. Метод сетевого оператора
Для решения задачи используем метод сетевого оператора [4-6]. Метод позволяет находить математические выражения, построенные на следующих множествах:
- множество переменных
![]() ,
, ![]() ,
, ![]() ; (9)
; (9)
- множество параметров
![]() ,
, ![]() ,
, ![]() ; (10)
; (10)
- множество унарных операций
![]() ; (11)
; (11)
- множество бинарных операций
![]() . (12)
. (12)
Сетевой оператор - это ориентированный граф, в котором каждому узлу-источнику соответствует элемент из множеств переменных или параметров, всем остальным узлам – номер бинарной операции, а каждой дуге соответствует унарная операция.
Для представления сетевого оператора в памяти компьютера используем матрицу сетевого оператора
![]() ,
, ![]() , (13)
, (13)
где ![]() - число узлов в сетевом операторе.
- число узлов в сетевом операторе.
Матрица сетевого оператора совпадает по структуре с матрицей смежности графа сетевого оператора. Вместо единиц матрицы смежности, указывающих на дуги графа, установим номера связанных с соответствующими дугами унарных операций, ![]() , если дуга
, если дуга ![]() связана с операцией
связана с операцией ![]() . На главной диагонали ставим номера бинарных операций,
. На главной диагонали ставим номера бинарных операций, ![]() , если узел
, если узел ![]() связан с бинарной операцией
связан с бинарной операцией ![]() .
.
В сетевом операторе узлы нумеруют так, чтобы, номер узла, откуда дуга выходит, был меньше номера узла, куда дуга входит, ![]()
![]() , Тогда матрица сетевого оператора будет иметь верхний треугольный вид. По матрице сетевого оператора можно вычислить значение математического выражения, для этой цели вводят дополнительные три вектора для указания номеров узлов для переменных, параметров и выходов.
, Тогда матрица сетевого оператора будет иметь верхний треугольный вид. По матрице сетевого оператора можно вычислить значение математического выражения, для этой цели вводят дополнительные три вектора для указания номеров узлов для переменных, параметров и выходов.
Приведем наиболее часто употребляемые унарные и бинарные операции.
![]() ,
, 
![]() ,
, ![]() ,
,  ,
, 
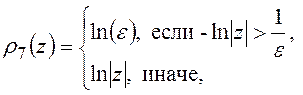
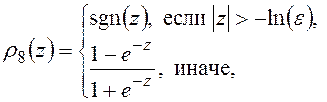
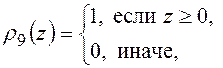 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,  ,
, 

![]() ,
, 

 ,
,  ,
, 
 ,
, 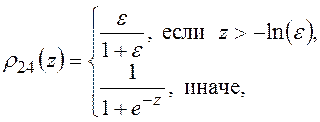 (15)
(15)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() . (16)
. (16)
Для бинарных операций (16) имеем следующие единичные элементы:
![]() ,
, ![]() ,
, 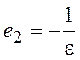 ,
,  ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . (17)
. (17)
Матрица ![]() сетевого оператора размерностью
сетевого оператора размерностью ![]() построена на множествах из
построена на множествах из ![]() переменных,
переменных, ![]() параметров,
параметров, ![]() унарных операций и
унарных операций и ![]() бинарных операций. Матрица позволяет описывать
бинарных операций. Матрица позволяет описывать
 , (18)
, (18)
где
 ,
,
математических выражений.
Сетевые операторы, которые имеют матрицы одинаковых размеров и одинаковые номера узлов источников для переменных, параметров и выходов называем подобными.
Для организации целенаправленного поиска оптимального сетевого оператора определим метрику на множестве подобных сетевых операторов, как сумму количества отличий между матрицами
 , (19)
, (19)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Если ![]() и
и ![]() , то говорим, что расстояние между сетевыми операторами
, то говорим, что расстояние между сетевыми операторами ![]() и
и ![]() равно
равно ![]() .
.
![]()
![]() -окрестностью сетевого оператора
-окрестностью сетевого оператора ![]() называем подмножество
называем подмножество ![]() , сетевых операторов, которые находятся на расстоянии не более
, сетевых операторов, которые находятся на расстоянии не более ![]() от сетевого оператора
от сетевого оператора ![]() ,
, ![]() ,
, ![]() .
.
Пусть мы имеем функцию![]() на множестве сетевых операторов. Тогда считаем, что функция
на множестве сетевых операторов. Тогда считаем, что функция ![]() достигает локального минимума на множестве сетевых операторов, если
достигает локального минимума на множестве сетевых операторов, если ![]() такой, что
такой, что ![]() ,
, ![]() .
.
Пусть ![]() оператор вариации или просто вариация сетевого оператора
оператор вариации или просто вариация сетевого оператора
![]() . (20)
. (20)
Элементарной вариацией сетевого оператора называем вариацию, удовлетворяющую условию
![]() . (21)
. (21)
Условие локального минимума функции ![]() имеет вид
имеет вид
![]() . (22)
. (22)
Элементарные вариации сетевого оператора могут отличаться друг от друга. Для сетевого оператора достаточно использовать следующие вариации: 0 – замена унарной операции, 1 - замена бинарной операции, 2 - добавление унарной операции, 3 – удаление унарной операции. При выполнении элементарной вариации 3 следует учитывать, что столбцы и строки сетевого оператора, которые не соответствуют узлам-источникам, не могут быть нулевыми. Для описания вариации используем вектор из четырех компонентов
![]() , (23)
, (23)
где ![]() - номер вариации,
- номер вариации, ![]() - номер строки,
- номер строки, ![]() - номер унарной или бинарной операции.
- номер унарной или бинарной операции.
Для организации поиска оптимального сетевого оператора ![]() используем упорядоченные наборы элементарных вариаций
используем упорядоченные наборы элементарных вариаций
![]() , (24)
, (24)
![]() . (25)
. (25)
Алгоритм поиска оптимального математического выражения включает следующие операции:
1. Задаем сетевой оператор ![]() , который, по мнению исследователя, наиболее близко описывает искомое решение. Данный сетевой оператор называем базисным.
, который, по мнению исследователя, наиболее близко описывает искомое решение. Данный сетевой оператор называем базисным.
2. Генерируем наборы вариаций ![]() ,
, ![]() , и вычисляем значения целевой функции для каждого нового сетевого оператора
, и вычисляем значения целевой функции для каждого нового сетевого оператора ![]() .
.
3. Если найден сетевой оператор с лучшим, чем у базисного сетевого оператора значением целевой функции, то заменяем базисный сетевой оператор.
4. Если ![]() , то
, то ![]() .
.
Вероятность ![]() нахождения оптимального сетевого оператора с помощью рассмотренного алгоритма зависит от количества
нахождения оптимального сетевого оператора с помощью рассмотренного алгоритма зависит от количества ![]() сгенерированных наборов вариаций:
сгенерированных наборов вариаций:
![]() . (26)
. (26)
3. Пример
В качестве примера рассмотрим химическую реакцию синглетного кислорода [8]
Дифференциальные уравнения (3), описывающие изменения концентраций веществ реакции, имеют вид
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() - неизвестная функция трех аргументов,
- неизвестная функция трех аргументов, ![]() - неизвестные значения постоянных параметров,
- неизвестные значения постоянных параметров, ![]() .
.
Для системы дифференциальных уравнений заданы начальные условия:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Уравнения баланса (5) имеют вид
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В качестве параметра оценки изменения концентраций веществ, участвующих в химической реакции, используем величину интенсивности
 .
.
Экспериментальные значения интенсивностей и моменты времени, в которые она определена, приведены в табл.1.
Для решения задачи использовали метод сетевого оператора. Для поиска решения использовали вариационный генетический алгоритм с множественным базисом. Алгоритм имел следующие значения параметров: количество возможных решений в начальной популяции – 512; число поколений – 128; число возможных скрещиваемых пар в поколении – 256; число вариаций в одном решении – 4; вероятность мутации 0.7; число базисов – 5; число элитарных решений 12; число поколений между сменой базисов – 16.
Таблица 1 Экспериментальные данные
|
|
|
|
0 | 9.9452e-1 | 7.4139e-1 | 4.7645e-1 |
5.4882e-3 | 9.9452e-1 | 7.6284e-1 | 4.6634e-1 |
2.1722e-2 | 9.7851e-1 | 7.8800e-1 | 4.5475e-1 |
4.7246e-2 | 9.5385e-1 | 8.1096e-1 | 4.4443e-1 |
5.8350e-2 | 9.4332e-1 | 8.2000e-1 | 4.4043e-1 |
8.0944e-2 | 9.2225e-1 | 8.4518e-1 | 4.2947e-1 |
1.0172e-1 | 9.0328e-1 | 8.5800e-1 | 4.2401e-1 |
1.1463e-1 | 8.9169e-1 | 8.8418e-1 | 4.1305e-1 |
1.3783e-1 | 8.7125e-1 | 9.0740e-1 | 4.0357e-1 |
1.4803e-1 | 8.6240e-1 | 9.1841e-1 | 3.9915e-1 |
1.7553e-1 | 8.3901e-1 | 9.5718e-1 | 3.8397e-1 |
1.9994e-1 | 8.1878e-1 | 9.5223e-1 | 3.8588e-1 |
2.1132e-1 | 8.0951e-1 | 9.7710e-1 | 3.7640e-1 |
2.3904e-1 | 7.8738e-1 | 9.9004e-1 | 3.7156e-1 |
2.7197e-1 | 7.6188e-1 | 1.0159e+0 | 3.6208e-1 |
2.8449e-1 | 7.5240e-1 | 1.0394e+0 | 3.5366e-1 |
3.1348e-1 | 7.3090e-1 | 1.0556e+0 | 3.4798e-1 |
3.2858e-1 | 7.1995e-1 | 1.0889e+0 | 3.3660e-1 |
3.5197e-1 | 7.0330e-1 | 1.1265e+0 | 3.2417e-1 |
3.6797e-1 | 6.9213e-1 | 1.1415e+0 | 3.1933e-1 |
3.8207e-1 | 6.8244e-1 | 1.1812e+0 | 3.0690e-1 |
4.0297e-1 | 6.6833e-1 | 1.2062e+0 | 2.9932e-1 |
4.1854e-1 | 6.5801e-1 | 1.2218e+0 | 2.9469e-1 |
4.2592e-1 | 6.5317e-1 | 1.2612e+0 | 2.8331e-1 |
4.4218e-1 | 6.4264e-1 | 1.2830e+0 | 2.7721e-1 |
4.5537e-1 | 6.3421e-1 | 1.3092e+0 | 2.7005e-1 |
4.6471e-1 | 6.2831e-1 | 1.3408e+0 | 2.6163e-1 |
4.8162e-1 | 6.1778e-1 | 1.3670e+0 | 2.5489e-1 |
5.0299e-1 | 6.0472e-1 | 1.3819e+0 | 2.5110e-1 |
5.1737e-1 | 5.9609e-1 | 1.3971e+0 | 2.4732e-1 |
5.4788e-1 | 5.7817e-1 | 1.4073e+0 | 2.4480e-1 |
5.6293e-1 | 5.6954e-1 | 1.4229e+0 | 2.4101e-1 |
5.8689e-1 | 5.5605e-1 | 1.4512e+0 | 2.3427e-1 |
6.0408e-1 | 5.4658e-1 | 1.4721e+0 | 2.2943e-1 |
6.1220e-1 | 5.4216e-1 | 1.5057e+0 | 2.2185e-1 |
6.2628e-1 | 5.3458e-1 | 1.5356e+0 | 2.1532e-1 |
6.4578e-1 | 5.2425e-1 | 1.5765e+0 | 2.0669e-1 |
6.5262e-1 | 5.2068e-1 | 1.6224e+0 | 1.9742e-1 |
6.7141e-1 | 5.1099e-1 | 1.6671e+0 | 1.8879e-1 |
6.9223e-1 | 5.0046e-1 | 1.6920e+0 | 1.8416e-1 |
7.0195e-1 | 4.9562e-1 | 1.7631e+0 | 1.7152e-1 |
7.1866e-1 | 4.8740e-1 | 1.7904e+0 | 1.6689e-1 |
1.8185e+0 | 1.6227e-1 | 3.3185e+0 | 3.621e-2 |
2.0544e+0 | 1.2817e-1 | 3.3418e+0 | 3.537e-2 |
2.1171e+0 | 1.2038e-1 | 3.3718e+0 | 3.4328e-2 |
2.1401e+0 | 1.1764e-1 | 3.3964e+0 | 3.3494e-2 |
2.1821e+0 | 1.1280e-1 | 3.4216e+0 | 3.2661e-2 |
2.2338e+0 | 1.0712e-1 | 3.4880e+0 | 3.0562e-2 |
2.2518e+0 | 1.0523e-1 | 3.4877e+0 | 3.0571e-2 |
2.2986e+0 | 1.0039e-1 | 3.5514e+0 | 2.8683e-2 |
2.3569e+0 | 9.4710e-2 | 3.6515e+0 | 2.5951e-2 |
2.3748e+0 | 9.3033e-2 | 3.7627e+0 | 2.3220e-2 |
2.3953e+0 | 9.1144e-2 | 3.8088e+0 | 2.2175e-2 |
2.4281e+0 | 8.8202e-2 | 3.8179e+0 | 2.1974e-2 |
2.4256e+0 | 8.8422e-2 | 3.8566e+0 | 2.1140e-2 |
2.4619e+0 | 8.5269e-2 | 3.8561e+0 | 2.1150e-2 |
2.4718e+0 | 8.4435e-2 | 3.9068e+0 | 2.0105e-2 |
2.4944e+0 | 8.2547e-2 | 3.9063e+0 | 2.0114e-2 |
2.5175e+0 | 8.0659e-2 | 3.9487e+0 | 1.9280e-2 |
2.5520e+0 | 7.7927e-2 | 3.9481e+0 | 1.9290e-2 |
2.5905e+0 | 7.4985e-2 | 3.9477e+0 | 1.9300e-2 |
2.6572e+0 | 7.0146e-2 | 3.9044e+0 | 2.0153e-2 |
2.6845e+0 | 6.8258e-2 | 3.9467e+0 | 1.9319e-2 |
2.7125e+0 | 6.6370e-2 | 4.0375e+0 | 1.7641e-2 |
2.7414e+0 | 6.4480e-2 | 4.0370e+0 | 1.7650e-2 |
2.8019e+0 | 6.0696e-2 | 4.0365e+0 | 1.7660e-2 |
2.8335e+0 | 5.8808e-2 | 4.0360e+0 | 1.7669e-2 |
2.8333e+0 | 5.8817e-2 | 4.0354e+0 | 1.7678e-2 |
2.8960e+0 | 5.5242e-2 | 4.0349e+0 | 1.7688e-2 |
2.8959e+0 | 5.5251e-2 | 4.0343e+0 | 1.7697e-2 |
2.9875e+0 | 5.0411e-2 | 4.1472e+0 | 1.5809e-2 |
3.0477e+0 | 4.7469e-2 | 4.2896e+0 | 1.3710e-2 |
3.0475e+0 | 4.7478e-2 | 4.3523e+0 | 1.2877e-2 |
3.0473e+0 | 4.7488e-2 | 4.4369e+0 | 1.1832e-2 |
3.0650e+0 | 4.6654e-2 | 4.4361e+0 | 1.1842e-2 |
3.0876e+0 | 4.5610e-2 | 4.4353e+0 | 1.1851e-2 |
3.1299e+0 | 4.3722e-2 | 4.4345e+0 | 1.1861e-2 |
3.1741e+0 | 4.1833e-2 | 4.6079e+0 | 9.9725e-3 |
3.1738e+0 | 4.1843e-2 | 4.5066e+0 | 1.1036e-2 |
3.1736e+0 | 4.1852e-2 | 4.5057e+0 | 1.1046e-2 |
3.2198e+0 | 3.9964e-2 | 4.5049e+0 | 1.1055e-2 |
3.2195e+0 | 3.9974e-2 | 4.5040e+0 | 1.1064e-2 |
3.2624e+0 | 3.8296e-2 | 4.5032e+0 | 1.1074e-2 |
3.2901e+0 | 3.725e-2 | 4.6023e+0 | 1.0029e-2 |
3.3185e+0 | 3.621e-2 | 4.5805e+0 | 1.0249e-2 |
3.3418e+0 | 3.537e-2 | 4.6880e+0 | 9.2046e-3 |
3.3718e+0 | 3.4328e-2 | 4.6867e+0 | 9.2147e-3 |
3.3964e+0 | 3.3494e-2 | 4.5984e+0 | 1.0067e-2 |
В результате был получен сетевой оператор
\
 ,
,
который, соответствует следующему уравнению
![]()
 , (27)
, (27)
где
![]() . (28)
. (28)
Для параметров ![]() получены следующие значения:
получены следующие значения: ![]() ,
, ![]() ,
, ![]() . График экспериментальных и вычисленных значений интенсивностей, полученных с использованием полученных функций
. График экспериментальных и вычисленных значений интенсивностей, полученных с использованием полученных функций ![]() приведен на рис. 1.
приведен на рис. 1.

Рис. 1 Экспериментальные и расчетные значения интенсивностей
Заключение
Из сравнения графиков, представленных на рис. 1 можно сделать вывод о высокой точности полученной математической модели химической реакции. В результате расчетов можно выдвинуть предположение об уточнении закона взаимодействия веществ Гульденберга-Ваага, концентрации веществ при их взаимодействии пропорциональны произведению полиномов от концентраций каждого вещества [7].
Работа выполнена по гранту РФФИ № 12-07-00324-а. «Структурная и параметрическая идентификация кинетических моделей реакций нейтрального металлокомплексного катализа».
Список литературы
1. Koza J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection. Cambridge, Massachusetts, London, MA: MIT Press, 1992. 819 p.
2. O’Neill M. Automatic Programming in an Arbitrary Labguage: Evolving Programs in Grammatical Evolution: PhD thesis. University of Limerick, 2001. 163 p.
3. Zelinka I. Analytic programming by Means of Soma Algorithm // Proc. 8th International Conference on Soft Computing Mendel’02. Brno, Czech Republic, 2002. P. 93-101.
4. Дивеев А.И. Метод сетевого оператора. М.: ВЦРАН, 2010. 178 с.
5. Дивеев А.И., Софронова Е.А. Метод сетевого оператора и его применение в задачах управления. М.: РУДН, 2012. 182 с.
6. Diveev A.I., Sofronova E.A. The Network Operator Method for Search of the Most Suitable Mathematical Equation // In the book “Bio-Inspired Computational Algorithms and Their Applications” / Edited by Shangce Gao. Croatia: InTech, 2012. P. 19-42.
7. Слинько М.Г. Основы и принципы математического моделирования каталитических процессов. Новосибирск: Институт катализа им. Г.К. Борескова СО РАН, 2004. 488 с.
8. Овчинников М.Ю., Юнусов А.А., Хурсан С.Л., Губайдуллин И.М. Моделирование генерации синглетного кислорода при разложении диметилдиоксирана с использованием технологии OpenMP // Параллельные вычислительные технологии (ПаВТ’2012) : труды международной научной конференции (Новосибирск, 26-30 марта 2012 г.). Челябинск: Издательский центр ЮУрГУ, 2012. С. 735-736.
Публикации с ключевыми словами: идентификация, генетическое программирование, метод сетевого оператора
Публикации со словами: идентификация, генетическое программирование, метод сетевого оператора
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



