научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#6 Июнь 2005
П. А. Бондарев, д-р техн. наук, проф., Р. А. Проскурин, 45 Центральный научно-исследовательский
институт Министерства обороны Российской Федерации
Обучение нейросети на базе шарового метода оптимизации Ньютона
Приведено описание разработанного метода оптимизации второго порядка. Метод позволяет повысить эффективность обучения монотонных сетей. Формализация базовых составляющих обучения осуществляется на основе обобщенного правила Хебба.
В настоящее время активно развивается "новая волна" исследований в области нейронных (нейроподобных) сетей. Модели нейронных сетей разрабатываются давно (особенно интенсивно — в конце пятидесятых и начале шестидесятых годов), но только в последнее время созрели научные и технические предпосылки для их технической реализации в форме нейрокомпьютеров. Естественно, что разные модели порождают различного типа нейроподобные сети и, соответственно, разные нейрокомпьютеры, эффективность которых при решении прикладных задач также различна. В связи с этим возникает проблема поиска или разработки таких моделей нейронных сетей, которые, с одной стороны, были бы наиболее удобны для реализации с помощью существующих технических и технологических средств, а с другой, могли бы обеспечить решение возможно более широкого круга задач искусственного интеллекта.
В рамках одного из возможных направлений решения этой задачи предлагается строить нейроподобную сеть на основе разработанного метода оптимизации второго порядка — шарового метода Ньютона. Нейроподобная сеть в актах двойственного функционирования предоставляет все необходимые процедуры для реализации этого метода [1].
Шаровой метод оптимизации Ньютона
Суть этого метода заключается в следующем. Пусть на Rn произвольно выбрана норма || • ||. В качестве матричной нормы для матрицы порядка n x п будет использоваться операторная норма, соответствующая || • ||.
Пусть ![]() ; множество
; множество ![]() назовем
шаром со срединной точкой z и радиусом ζ.
Введем обозначения:
назовем
шаром со срединной точкой z и радиусом ζ.
Введем обозначения:
![]() — центр
шара;
— центр
шара;
![]() — радиус
шара.
— радиус
шара.
Если ![]() , то множество таких шаров, для
которых выполняется соотношение
, то множество таких шаров, для
которых выполняется соотношение ![]() , будет обозначаться
, будет обозначаться ![]() .
.
Множество всех шаров ![]() , для которых имеет место
, для которых имеет место ![]() обозначим Kn0(Rn).
обозначим Kn0(Rn).
Отметим ряд свойств введенной конструкции:
·
всякий шар ![]() является компактным и
выпуклым;
является компактным и
выпуклым;
·
включение ![]() справедливо, если и только
если
справедливо, если и только
если ![]() ;
;
·
пусть ![]() и определяется соотношением
и определяется соотношением ![]() , тогда
, тогда ![]() , если и
только если
, если и
только если ![]() и
и ![]() ;
;
·
если ![]() , то множество всех шаров
, то множество всех шаров ![]() , где
, где ![]() лежит в
двойном конусе с вершиной в нуле и с определяющим углом α = arcsinλ..
лежит в
двойном конусе с вершиной в нуле и с определяющим углом α = arcsinλ..
В дальнейшем будет использоваться более узкое понятие — арифметический
шар. Пусть ![]() ,
, ![]() .
.
Определим две операции:
![]() (1)
(1)
![]() (2)
(2)
Заметим, что если ζ = 0, то соотношения (1), (2) являются обычными операциями с векторами в Rn. Очевидными также являются соотношения
![]()
Пусть ![]() и пусть
и пусть ![]() где
где ![]() — операция
пересечения;
— операция
пересечения; ![]() — пустое множество.
— пустое множество.
Тогда найдется, по крайней мере, один шар ![]() , для которого
, для которого ![]() и rad Z=min{radZ, radY}.
Если имеется более чем один шар, то всегда можно выбрать один для того, чтобы
определить операцию пересечения арифметических шаров.
и rad Z=min{radZ, radY}.
Если имеется более чем один шар, то всегда можно выбрать один для того, чтобы
определить операцию пересечения арифметических шаров.
Для специального случая евклидовой метрики как срединная точка x, так и радиус ζ, нового шара Z легко вычисляются по соотношениям
![]() (3)
(3)
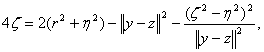 (4)
(4)
которые
справедливы при предположениях, не нарушающих общности ![]() при
при ![]() .
.
Для построения методов нелинейного оценивания определим специальный шаровой оператор.
Пусть ![]() будет регулярной n x n матрицей и
будет регулярной n x n матрицей и ![]() , причем
, причем ![]() . Тогда
регулярный шаровой оператор L определяется
шаровозначным оператором
. Тогда
регулярный шаровой оператор L определяется
шаровозначным оператором
![]()
![]()
Оператор L будет обозначаться также
выражением L = ![]() .
.
Любой шаровой оператор можно рассматривать как операторный шар, соответствующий соотношению
![]() (5)
(5)
причем всегда верны утверждения:
·
![]() ;
;
·
![]() , если и только если
справедливо
, если и только если
справедливо
![]() , где Е —
единичная матрица.
, где Е —
единичная матрица.
Это означает, что относительная погрешность между матрицами ![]() и
и ![]() ограничена
величиной λ < 1;
ограничена
величиной λ < 1;
·
если ![]() , то
, то ![]() — регулярная матрица
и для ее обращения имеет место неравенство
— регулярная матрица
и для ее обращения имеет место неравенство
![]() (6)
(6)
Отсюда
следует, что относительная погрешность между ![]() и
и ![]() ограничена. Если кроме
того имеет место
ограничена. Если кроме
того имеет место ![]() , то правая часть последнего
неравенства меньше единицы, а следовательно,
, то правая часть последнего
неравенства меньше единицы, а следовательно, ![]() является регулярным
оператором.
является регулярным
оператором.
Рассмотрим класс функций F, состоящий из
множества всех функций b: B -> Rn таких, что
для каждого множества С вида ![]() при
при ![]() существует
регулярная n x n
матрица и вещественное число
существует
регулярная n x n
матрица и вещественное число ![]() такое, что
такое, что ![]() и справедливо
и справедливо
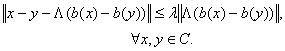 (7)
(7)
Если имеется более одного λ(C) и/или ![]() (C),
то выбирается всегда только один шар.
(C),
то выбирается всегда только один шар.
Очевидно, существует эквивалентное определение класса функций F0. Класс F
состоит из всех функций b: B → Rn,
для которых существует b-1 на b(B) и которые
удовлетворяют условию Липшица на С. Отметим ряд свойств функции b ![]() F:
F:
1. Имеется по крайней мере один нуль функции b ![]() F
на B.
F
на B.
2. На множестве C любая функция b ![]() F
удовлетворяет условию Липшица
F
удовлетворяет условию Липшица
 (8)
(8)
3. Пусть b ![]() F будет дифференцируема по Фреше
в точке x
F будет дифференцируема по Фреше
в точке x ![]() B и пусть Ф(x) будет
якобианом, тогда Ф(x)-1 существует и
ограничена:
B и пусть Ф(x) будет
якобианом, тогда Ф(x)-1 существует и
ограничена:
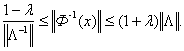 (9)
(9)
Кроме того, относительная погрешность между ![]() и Ф-1(x) также может быть ограничена:
и Ф-1(x) также может быть ограничена:
![]() (10)
(10)
4. Пусть b ![]() F будет дифференцируемой по Фреше на всей области C тогда
F будет дифференцируемой по Фреше на всей области C тогда
![]() (11)
(11)
5. (Критерий b ![]() F). Пусть существует
F). Пусть существует ![]() для всех x
и y из множества C,
причем
для всех x
и y из множества C,
причем ![]() .
.
Последнее соотношение верно, если b
удовлетворяет одной из теорем о среднем. Пусть на C
существует ![]() и пусть выполняется включение
и пусть выполняется включение ![]() для всех x, y
для всех x, y ![]() C при регулярном шаровом операторе L
= <<
C при регулярном шаровом операторе L
= <<![]() ,
λ>>. Тогда верно соотношение:
,
λ>>. Тогда верно соотношение:
![]() (12)
(12)
Для построения численных методов нелинейного оценивания определим специальный шаровой оператор.
Пусть ![]() при a
при a ![]() B.
B.
Пусть <<![]() , λ >> будет
регулярным шаровым оператором, соответствующим C=A
, λ >> будет
регулярным шаровым оператором, соответствующим C=A![]() B. Тогда определим
оператор
B. Тогда определим
оператор
![]()
![]() (13)
(13)
Очевидно, что N= N(C).
Для введенного оператора характерны следующие свойства:
![]() (14)
(14)
![]() (15)
(15)
Следовательно, как mid Nx, так и rad Nx непрерывны на В.
2. Если ![]() , если и только если x*=N(x*).
Следовательно, нули функции b являются на C в точности неподвижными точками оператора N.
, если и только если x*=N(x*).
Следовательно, нули функции b являются на C в точности неподвижными точками оператора N.
3. Если ![]() и
и ![]() , то на C не существует нуля функции b.
, то на C не существует нуля функции b.
4. Пусть b ![]() F. Предположим, что b
дифференцируема по Фреше на C. Пусть на C существует
F. Предположим, что b
дифференцируема по Фреше на C. Пусть на C существует ![]() и пусть включение
и пусть включение ![]() для всех x, z
для всех x, z ![]() C. Пусть найдется одна точка x
C. Пусть найдется одна точка x ![]() C
такая, что Nx
C
такая, что Nx![]() C.
Тогда b имеет точно один нуль x*
C.
Тогда b имеет точно один нуль x* ![]() C.
C.
5. Если x, x*
![]() C и b(x*) = 0, то x*
C и b(x*) = 0, то x* ![]() Nx. Это означает, что если применить шаровой оператор
(13) к произвольной точке х
Nx. Это означает, что если применить шаровой оператор
(13) к произвольной точке х ![]() C,
получается граница погрешности нуля x* функции b в C. Другими словами,
применение оператора не приводит к потере нуля функции b.
C,
получается граница погрешности нуля x* функции b в C. Другими словами,
применение оператора не приводит к потере нуля функции b.
6. Пусть существует последовательность {![]() }, причем
}, причем ![]()
![]() C
для υ = 0, 1, ..., и lim xυ = x*, где
C
для υ = 0, 1, ..., и lim xυ = x*, где
b(x*) = 0. Тогда x* ![]() Nxυ
для υ = 0, 1, 2, ...,.
Nxυ
для υ = 0, 1, 2, ...,.
 (16)
(16)
Это означает, что применение оператора (13) к сходящейся
последовательности {![]() } дает последовательность
границ погрешностей {Nxυ},
которая также сходится в смысле соотношений (16).
} дает последовательность
границ погрешностей {Nxυ},
которая также сходится в смысле соотношений (16).
Нейросеть в процессе обучения
Серьезной проблемой при обучении нейроподобной сети реальным задачам является то, что адаптивный ландшафт сети не соответствует гладкой и точно заданной функции оценки [2]. Построение сети на базе вышеописанного метода позволяет разрешить эту проблему. Процесс разворачивается следующим образом. В ходе обучения нейронной сети базовые составляющие можно обозначить так: поисковая активность, поощрение успеха, наказание неуспеха. При этом выделяются градации оценки: обычно две (успех — неуспех) или три (успех — нейтральный исход — неудача). В такой ситуации уже нет гладкой адаптивной функции оценки и поэтому невозможно применять простейшие методы поиска экстремума.
Для построения новых алгоритмов оптимизации нейронных сетей необходимо формализовать базовые компоненты (активность—поощрение — наказание). Формализация возможна с помощью обобщенного правила Хебба. Это правило формализует наказания и поощрения: наказание состоит в усилении тормозных и ослаблении возбуждающих связей; поощрение, наоборот, — в усилении возбуждающих и ослаблении тормозных. Учитывая показатели чувствительности, нужно модифицировать не все связи, а только те, которые вносили существенный вклад в данный успех или неудачу. В чисто коннекционистских сетях обычно за показатель чувствительности для синаптического веса принимается модуль переданного по нему сигнала. При использовании правила Хебба предполагается, что наказание разрушит ошибочные действия, а поощрение усилит успешные. Наказание именно разрушает, а не исправляет, ибо нет направления спуска и неясно, куда "лучше". Тенденция неправильно действовать ослабляется. За счет поисковой активности появляются удачи, которые фиксируются поощрением. После некоторого времени обучения поисковая активность становится не совсем случайной — появляется ряд запретов, с одной стороны, и преимущественных направлений — с другой.
Для нейронной сети, состоящей из большого числа нейронов и синаптических связей очень сложно формализовать понятия "тормозные и возбуждающие связи", так как увеличение выходного сигнала для одного нейрона может привести к уменьшению для другого. Трудно разделить параметры и сигналы на возбуждающие и тормозящие, для нескольких тактов функционирования ситуация еще больше усложняется.
Невозможность четкой формализации в общем случае приводит к необходимости ввода сетей специальной структуры. Эти сети конструируются на базе дополнительно вводимого понятия монотонного функционального элемента. В качестве алгоритма обучения (оптимизации) монотонных функциональных элементов и, соответственно, монотонных сетей используется шаровой метод.
Для определения возбуждения и торможения в случаях большого числа параметров и выходных сигналов используется понятие порядка в векторных пространствах, который задается с помощью замкнутого выпуклого телесного двойного конуса Q, в котором лежит множество всех шаров.
Определим монотонный функциональный элемент для дальнейшего построения из них монотонных сетей. Функциональный элемент f по вектору входов A и вектору параметров α вычисляет вектор выходов f(A, α). Элемент f называется монотонным по входам, если в пространстве входов и пространстве выходов (Rfin и Rfout) определены векторные порядки с конусами положительных элементов Qfin и Qfout и для любого вектора параметров а f (•, α) — монотонно возрастающее отображение из Rfin в Rfout. Аналогично, f называется монотонным по параметрам, если в пространстве параметров Rfp и пространстве выходов Rfout определены векторные порядки с конусами положительных элементов Qfp и Qfout и для любого вектора входов Af(-,A) — монотонно возрастающее отображение из Rfp в Rfout. Элемент f называется монотонным, если он монотонен и по входам и по параметрам.
Примером монотонного элемента может служить нейронная сеть из пороговых нейронов с линейными синапсами, имеющими неотрицательные веса, с линейными сумматорами перед входами нейронов и подачей внешних входных сигналов на нейроны.
Важным преимуществом нейронной сети (не связанным с высоким уровнем параллелизма) при оценке качества функционирования является то, что для нейросетевой структуры по циклу функционирования нетрудно оценить значимость каждого параметра в получении данного ответа. Поощрение состоит в увеличении значимых параметров, наказание — в их уменьшении. Размер увеличений и уменьшений зависит от:
· значения параметра;
· момента обратного функционирования T, на котором параметр был включен в список значимых;
· места соответствующего элемента в структуре сети.
Проведенное сравнение с более простыми методами оптимизации показывает, что поощрение и наказание сильно различаются. Поощрение служит фиксации полезного навыка, а наказание уменьшает параметры, определяющие неправильный ответ, но не ведет к улучшению. Оно разрушает неправильные навыки с тем, чтобы их места заняли случайно найденные и поощренные правильные.
Для процесса поощрения можно провести аналогию с одномерной оптимизацией. Для наказания по результатам решения одного примера такая аналогия невозможна. Работа сразу со страницей примеров позволяет ввести аналог одномерной оптимизации для наказаний и существенно ускоряет обучение. Еще более качественные показатели обучения неиросети получаются при реализации шарового алгоритма в качестве алгоритма наказания. Качество достигается за счет преимуществ, предоставляемых шаровым методом.
Необходимо отметить, что после каждого цикла алгоритма и построения нового шара этот шаг оценивается — сеть решает все примеры страницы при новых значениях параметров. Определяются значения параметров сети, при которых оценка за решение примеров меняется с "хорошо" на "плохо". Для таких примеров выделяются значимые параметры и новый шар строится, когда положение этих значимых параметров нулевое. Дальше процесс продолжается до возникновения ухудшений в оценке. Когда это происходит, часть параметров очередного шара обращается в нуль, и так до тех пор, пока улучшение возможно. После наказания следует поощрение.
Постепенное увеличение значимых параметров для хорошо решаемых примеров приводит к тому, что дальнейшее их увеличение вызывает ухудшение оценки. Далее — снова наказание, потом поощрение и т. д. Процесс останавливается либо тогда, когда все примеры страницы решены хорошо, либо после заданного числа наказаний и поощрений. Последним выполняется поощрение. Если не все примеры страницы решены хорошо, то проводится случайный поиск — генерируются случайные сдвиги параметров. Принимаются только те из них, которые не ухудшают решений. Потом снова наказание и поощрение и т. д.
Когда правильно решены все примеры страницы, переход к следующей проводится специальным образом — с включением в новую страницу хорошо решаемых примеров с предыдущей. При описанном способе наказаний и поощрений необходимо такое включение всех или хотя бы части хорошо решаемых примеров с предыдущих страниц.
Математическое подтверждение вышеописанного алгоритма обучения строится в виде доказательства теоремы с использованием обозначений, введенных при описании шарового метода.
Теорема. Пусть b ![]() F. Функция b не имеет нуля
в B тогда и только тогда, когда алгоритм
останавливается. Функция b имеет (однозначно
определяемый) нуль x*
F. Функция b не имеет нуля
в B тогда и только тогда, когда алгоритм
останавливается. Функция b имеет (однозначно
определяемый) нуль x* ![]() B
тогда и только тогда, когда алгоритм продолжается неограниченно.
B
тогда и только тогда, когда алгоритм продолжается неограниченно.
В этом случае порождается последовательность шаров ![]() , для которой
, для которой ![]()
Последовательность
радиусов шаров сходится по крайней мере линейно и ![]()
Доказательство.
Если λ = 0, то b
является линейной функцией. В этом случае применение к x0
шарового оператора N производит точку x*.
Если x* ![]() B,
то алгоритм останавливается на начальном шаге. Если x*
B,
то алгоритм останавливается на начальном шаге. Если x*
![]() B, то алгоритм никогда не останавливается и дает
результат Zυ = <x*, 0> для всех υ
= 1, 2, ... Из этого следует, что без нарушения общности можно предположить,
что λ > 0.
B, то алгоритм никогда не останавливается и дает
результат Zυ = <x*, 0> для всех υ
= 1, 2, ... Из этого следует, что без нарушения общности можно предположить,
что λ > 0.
Допустим, что имеется (однозначно определяемый) нуль x* функции b на Z0 = В.
Тогда x* ![]() Nx0
в силу определения шарового оператора. Поэтому также x*
Nx0
в силу определения шарового оператора. Поэтому также x*
![]() Z, где Z определяется как
пересечение. Следовательно, алгоритм не останавливается в течение начального
шага.
Z, где Z определяется как
пересечение. Следовательно, алгоритм не останавливается в течение начального
шага.
Допустим, доказано уже, что x* ![]() Zυ. По построению
Zυ. По построению ![]() . Поэтому
. Поэтому ![]() , а это
влечет
, а это
влечет ![]() ,
где
,
где ![]() определяется
как пересечение. Следовательно, несправедливы утверждения
определяется
как пересечение. Следовательно, несправедливы утверждения ![]() , а поэтому алгоритм
не останавливается также и на υ-м шаге. Это
верно для всех υ = 0, 1, ... и означает,
что если x*
, а поэтому алгоритм
не останавливается также и на υ-м шаге. Это
верно для всех υ = 0, 1, ... и означает,
что если x* ![]() B,
то алгоритм не останавливается. Возможно и обратное доказательство того, что
если алгоритм не останавливается, то последовательность шаровых срединных точек
сходится к предельной точке. При этом определяется
B,
то алгоритм не останавливается. Возможно и обратное доказательство того, что
если алгоритм не останавливается, то последовательность шаровых срединных точек
сходится к предельной точке. При этом определяется ![]() для шара υ ≥ 1, и выбирается
для шара υ ≥ 1, и выбирается ![]() и
и ![]() так, чтобы
выполнялся критерий принадлежности функции f
классу F. Определив оператор N с
выбранными константами и выполнив шаги в соответствии с вышеописанным
алгоритмом, приходим к заключению, что для b
так, чтобы
выполнялся критерий принадлежности функции f
классу F. Определив оператор N с
выбранными константами и выполнив шаги в соответствии с вышеописанным
алгоритмом, приходим к заключению, что для b ![]() F все утверждения предыдущей теоремы верны, однако скорость
сходимости алгоритма квадратичная.
F все утверждения предыдущей теоремы верны, однако скорость
сходимости алгоритма квадратичная.
Схемная реализация шарового метода с помощью неиросети
Работу нейронной сети при вычислении сложной функции представляется так: на вход сети подаются значения переменных xi(i=1,…, n). На каждом шаге вычисляется функция fj(j=n+1,…, N). На выходе сети при данных значениях параметров получается сложная функция F(α, x).
Схема вычисления dF/dxi, dF/dαi; будет состоять из двух цепочек — прямой и обратной. Цепочка прямого функционирования, помимо вычисления, fj, будет включать еще вычисление частных производных этих функций по их аргументам. Для этого примем обозначения: fj, k — производная fj- по k-му аргументу (входу), fj, αm — производная fj по αm. Схематически такт прямого функционирования показан на рис. 1.
В ходе обратного функционирования вычисляются производные dF/dxi (обозначим их μi) при
i = 1, ..., n. Для вычисления dF/dα требуются дополнительные операции:
![]() (17)
(17)

Рис. 1. Такт прямого функционирования с вычислением частных производных простых функций
Суммирование ведется по всем j, для которых fj зависит от αp. Такт обратного функционирования изображен на рис. 2.
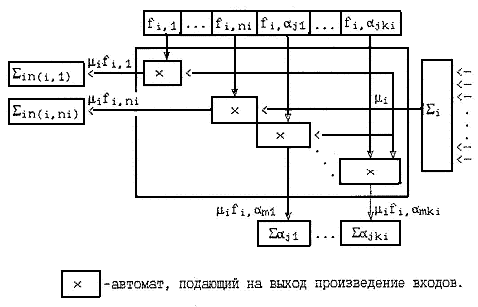
Рис. 2. Такт обратного функционирования нейросети
В качестве входов на каждый из автоматов, производящих умножение
(обозначим их ![]() ) подаются: частная производная
fi, вычисленная в ходе прямого
функционирования, и переменная обратного функционирования μi. Результат умножения подается на сумматор,
определяемый аргументом, по которому взята частная производная fi. Если это производная по j-му входу, то сигнал направляется туда, откуда при
прямом функционировании приходил вход, т. е. на Σin,(i, j).
Если же это производная по параметру αi,
то сигнал посылается на сумматор Σα. При обратном
функционировании выходы
) подаются: частная производная
fi, вычисленная в ходе прямого
функционирования, и переменная обратного функционирования μi. Результат умножения подается на сумматор,
определяемый аргументом, по которому взята частная производная fi. Если это производная по j-му входу, то сигнал направляется туда, откуда при
прямом функционировании приходил вход, т. е. на Σin,(i, j).
Если же это производная по параметру αi,
то сигнал посылается на сумматор Σα. При обратном
функционировании выходы ![]() соответствуют входам
соответствуют входам ![]() , вход —
выходу fi а
входной сумматор Σi — точке ветвления на
выходе fi. Входные адреса
соответствуют выходным и обратно.
, вход —
выходу fi а
входной сумматор Σi — точке ветвления на
выходе fi. Входные адреса
соответствуют выходным и обратно.
При организации обучения используются вторые производные функции ошибки. Вычислять всю матрицу вторых производных и хранить ее в памяти слишком сложно. Существует возможность вычислять градиенты от некоторых функций градиента H:
![]() (18)
(18)
где суммирование ведется по всем параметрам α.
Поскольку градиент Н вычисляется в параллельно-последовательном режиме сетью автоматов прямого и обратного функционирования, то можно организовать обратное функционирование этой сети для вычисления нужных производных. Это дважды обратное функционирование называется "back-back" процедурой. Если ограничиться случаем xiT = xiT(in), формулы прямого и первого обратного функционирования будут иметь вид:
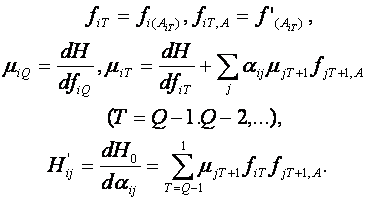 (19)
(19)
В обратно-обратном функционировании вычисляются производные функции оценки
![]() (20)
(20)
по параметрам αij.
Исходно H2 задана как функция H’ij - получаемых на выходе специальных сумматоров системы обратного функционирования. При обратно-обратном функционировании сумматоры заменяются точками ветвления, выходы — входами и на эти новые входы подаются частные производные H2(20).
Разработан новый метод обучения нейронной сети. По сравнению с существующими традиционными методами оптимизации этот метод обладает следующими преимуществами: позволяет получить хорошее начальное приближение при решении задач нелинейного оценивания; обладает квадратичной скоростью сходимости; дает возможность отыскания экстремума функций многих переменных, обладающих множеством локальных минимумов, поверхности уровня которых имеют овражную структуру, являющихся адаптивным графиком нейронной сети.
Список литературы
1. Барцев С. И., Гилев С. Е., Охонин В. А. Принцип двойственности в организации адаптивных сетей обработки информации // Динамика химических и биологических систем. Новосибирск: Наука, 1989. С. 6—55.
2. Горбань А. Н. Обучение нейронных сетей. М.: СП Пара-Граф, 1990. 159 с.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 7, 1998
НЕИРОСЕТИ И НЕЙРОКОМПЬЮТЕРЫ
Ключевые слова: Нейронные сети, обучение нейронных сетей, оптимизация, методы второго порядка, шаровой метод.
Публикации с ключевыми словами: оптимизация, нейросети, метод Ньютона
Публикации со словами: оптимизация, нейросети, метод Ньютона
Смотри также:
- Возможности применения параллельных методов вычисления в системе программирования на языке S-FLOGOL
- Разработка программной среды для моделирования и оптимизации складской политики двухэшелонных многопродуктовых цепей поставки
- Математическая модель взаимодействия предприятий по производству продуктов питания молочной отрасли АПК РФ
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



