научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2013
DOI: 10.7463/0113.0517977
УДК 539.3:62-27
Россия, МГТУ им. Н.Э. Баумана
dim.sm2@yandex.ru
Постановка задачи
Рассмотрим тонкую прямоугольную пластину (рис. 1) с размерами ![]() в плане и толщиной
в плане и толщиной ![]() .
.
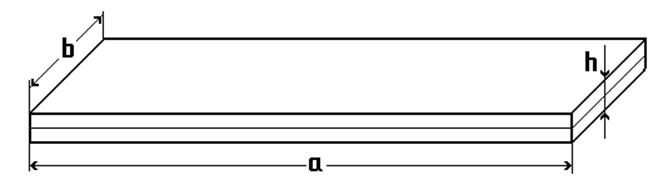
Рис. 1
Пусть каким-либо образом, например, путем приложения распределенного изгибающего момента постоянной интенсивности вдоль двух противоположных кромок длиной ![]() , пластина свернута в цилиндр радиуса
, пластина свернута в цилиндр радиуса ![]() и помещена в цилиндрическую полость того же радиуса (рис. 2).
и помещена в цилиндрическую полость того же радиуса (рис. 2).

Рис. 2
При таком сворачивании перемещения точек пластины оказываются сопоставимыми с габаритными размерами пластины. В работе [1] В.Д. Черненко получил аналитическое решение данной задачи в предположении, что пластина плотно прилегает к полости по всей поверхности. Техническое приложение решения дано в [2], где определены величины контактных усилий, возникающих при изгибе и сворачивании в цилиндр резинокордной конвейерной ленты. Предположение о плотном прилегании применимо в тех случаях, когда изгибная жесткость пренебрежимо мала по сравнению с жесткостью на растяжение-сжатие, что имеет место для резинокордной ленты. В случае если пластина изготовлена из изотропного материала будет наблюдаться неплотное прилегание к внутренней поверхности цилиндра, и возникнет зона отслоения. Такая задача относится к классу контактных задач с неизвестной заранее областью контакта [3]. В статье [4] В.Л. Бидерман и С.В. Бояршинов получили аналитическое решение контактной задачи о посадке упругого кольца на вал. При этом упругое кольцо контактирует с жесткой цилиндрической поверхностью, зона контакта заранее неизвестна. Ими были определены контактные усилия и найдено значение угла отслоения. Перемещения кольца при посадке на вал малы и поэтому задача, рассмотренная в [4] является геометрически линейной. В докладах [5, 6] был предложен и развит численный алгоритм решения геометрически нелинейных контактных задач, сочетающий в себе применение метода малых нагружений с методом стрельбы. При этом было получено и численное решение рассматриваемой задачи. В настоящей статье с использованием подходов, принятых в работах [1] и [4], найдено приближенное аналитическое решение задачи об изгибе изотропной пластины, помещенной в цилиндрическую полость, с учетом наличия зоны отслоения.
Условия равновесия на отслоенном и прилегающем участках
Следуя [2], будем считать, что срединная поверхность изогнутой пластины мало отличается от поверхности кругового цилиндра радиуса R, поэтому целесообразно деформацию пластины рассматривать в системе координат, связанной с поверхностью цилиндра. Считаем, что пластина находится в условиях цилиндрического изгиба, так что можно ограничиться рассмотрением деформаций в одной плоскости. При этом в отличие от [2], предполагается наличие зоны отслоения, размер которой определяется некоторым углом ![]() . Обычно [3, 4], распределение контактных усилий в подобных задачах принимается в соответствии с рис. 3: здесь q– распределенное по площади контактное давление постоянной интенсивности, Q1 и Q2 – усилия, распределенные вдоль границ зон контакта.
. Обычно [3, 4], распределение контактных усилий в подобных задачах принимается в соответствии с рис. 3: здесь q– распределенное по площади контактное давление постоянной интенсивности, Q1 и Q2 – усилия, распределенные вдоль границ зон контакта.
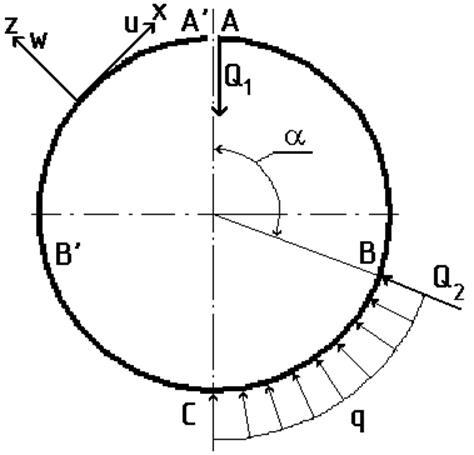
Рис. 3
Допустимость принятой силовой схемы должна быть подтверждена в ходе решения. При этом, как отмечалось в [7], принимаемое в подобных задачах распределение сил, противоречит предположению о плотном прилегании пластины к поверхности цилиндра на участке BC. Здесь пластина должна находиться в условиях чистого изгиба и при использовании теории пластин Кирхгофа-Клебша поперечная нагрузка ![]() должна быть равна нулю, а нагрузка должна быть представлена изгибающими моментами, приложенными к наружному контуру пластины. При принятой схеме нагрузок, должны каким-то образом, проявится противоречия при решении уравнений в перемещениях и удовлетворении граничным условиям. Как будет показано ниже, предположение о плотном прилегании на участке BC выполняется с некоторой погрешностью. Здесь будут перемещения, но они оказываются существенно меньше, чем в зоне отслоения AB.
должна быть равна нулю, а нагрузка должна быть представлена изгибающими моментами, приложенными к наружному контуру пластины. При принятой схеме нагрузок, должны каким-то образом, проявится противоречия при решении уравнений в перемещениях и удовлетворении граничным условиям. Как будет показано ниже, предположение о плотном прилегании на участке BC выполняется с некоторой погрешностью. Здесь будут перемещения, но они оказываются существенно меньше, чем в зоне отслоения AB.
Так как в направлении образующей цилиндра, в силу принятых допущений, пластина не изгибается, внутренние силовые факторы могут быть найдены из условий равновесия методом сечений. Силовые факторы действующие на отслоенном участке АВ показаны на рисунке 4.

Рис. 4
Записывая уравнения равновесия, получим:
 (1)
(1)
Здесь ![]() - погонная продольная сила,
- погонная продольная сила, ![]() - погонная поперечная сила,
- погонная поперечная сила, ![]() - погонный изгибающий момент,
- погонный изгибающий момент, ![]() - некоторый текущий угол. Принятые положительные направления силовых факторов, показаны на рис. 4.
- некоторый текущий угол. Принятые положительные направления силовых факторов, показаны на рис. 4.
Для прилегающего участка силовые факторы показаны на рис. 5:
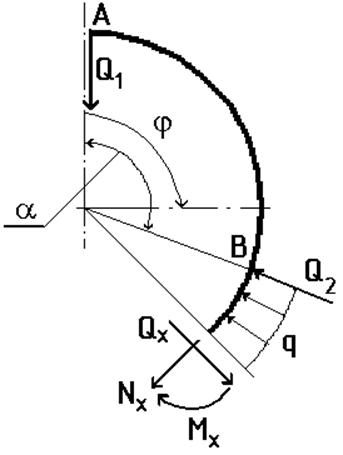
Рис. 5
Уравнения равновесия для участка ВС:
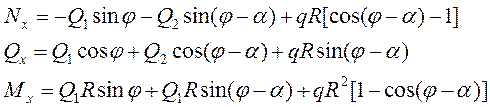 (2)
(2)
![]() - угол, характеризующий размер зоны отслоения.
- угол, характеризующий размер зоны отслоения.
Определение контактных сил и давления
На участке BC пластина в силу плотного прилегания к цилиндру находится в условиях чистого изгиба и момент на этом участке постоянный, чтобы на участке ВС выполнялось условие ![]() , из третьего уравнения системы (2) получим
, из третьего уравнения системы (2) получим
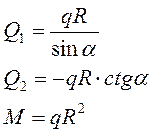 (3)
(3)
При чистом изгибе изгибающий момент связан с кривизной соотношением
. (4)
(4)
Где  цилиндрическая жесткость,
цилиндрическая жесткость, ![]() модуль упругости материала,
модуль упругости материала, ![]() коэффициент Пуассона. Из (4) следует
коэффициент Пуассона. Из (4) следует
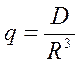 (5)
(5)
Таким образом, оказываются определенными значения всех контактных усилий.
Определение перемещений на отслоенном участке и размера зоны отслоения
Для определения неизвестного угла ![]() потребуется рассмотрение деформаций отслоенного участка АВ пластины. Как и при записи уравнений равновесия, будем считать, что срединная поверхность изогнутой пластины мало отличатся от поверхности кругового цилиндра радиуса
потребуется рассмотрение деформаций отслоенного участка АВ пластины. Как и при записи уравнений равновесия, будем считать, что срединная поверхность изогнутой пластины мало отличатся от поверхности кругового цилиндра радиуса ![]() и используем геометрические и физические уравнения цилиндрической оболочки[8]. В случае изгиба в одном направлении продольное усилие
и используем геометрические и физические уравнения цилиндрической оболочки[8]. В случае изгиба в одном направлении продольное усилие ![]() и изгибающий момент
и изгибающий момент ![]() связаны с компонентами перемещения
связаны с компонентами перемещения ![]() и
и ![]() соотношениями:
соотношениями:
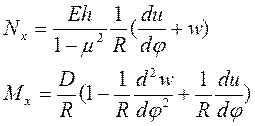 (6)
(6)
Первое слагаемое ![]() в формуле для момента
в формуле для момента ![]() учитывает момент, возникающий при сворачивании пластины в цилиндр. Положительные направления перемещений
учитывает момент, возникающий при сворачивании пластины в цилиндр. Положительные направления перемещений ![]() и
и ![]() показаны на рис. 3.
показаны на рис. 3.
Используя уравнения равновесия для зоны отслоения (1) и найденные значения силовых факторов (3) перепишем (6) в виде:
 (7)
(7)
После преобразований приходим к системе из двух дифференциальных уравнений для определения неизвестных перемещений ![]() и
и ![]() в зоне отслоения:
в зоне отслоения:
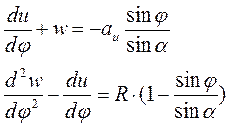 (8)
(8)
где 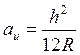 . Из системы (8) получим дифференциальное уравнение для определения
. Из системы (8) получим дифференциальное уравнение для определения ![]() :
:
 (9)
(9)
Общее решение уравнения (9):
 (10)
(10)
Неизвестные константы ![]() и
и ![]() , а так же угол отслоения
, а так же угол отслоения ![]() определяются из граничных условий. Потребуем выполнения на концах участка АВ равенства нулю поперечных перемещений, а в зоне сопряжения с прилегающим участком BC равенства нулю угла поворота:
определяются из граничных условий. Потребуем выполнения на концах участка АВ равенства нулю поперечных перемещений, а в зоне сопряжения с прилегающим участком BC равенства нулю угла поворота:
![]()
 (11)
(11)
Удовлетворяя граничным условиям, получим значения констант:
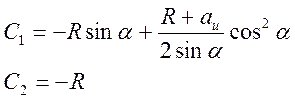 (12)
(12)
и трансцендентное уравнение для определения угла ![]() :
:
 (13)
(13)
Ввиду малости толщины пластины ![]() , коэффициент
, коэффициент ![]() , поэтому (13) можно приближенно переписать в виде:
, поэтому (13) можно приближенно переписать в виде:
 (14)
(14)
Уравнение (14) совпадает с полученным в [4] аналогичным уравнением в контактной задаче о посадке упругого кольца на вал. Значение угла ![]() , удовлетворяющее (14) будет таким же, как и в (4):
, удовлетворяющее (14) будет таким же, как и в (4): ![]() . При малых значениях
. При малых значениях ![]() решения (13) и (14) отличаются незначительно, так при
решения (13) и (14) отличаются незначительно, так при ![]() мм и
мм и ![]() мм, значения угла
мм, значения угла ![]() . Значения внутренних силовых факторов могут быть найдены по уравнению (6), а поперечного перемещения
. Значения внутренних силовых факторов могут быть найдены по уравнению (6), а поперечного перемещения ![]() по уравнению (10) с учетом значений констант (12). При вычислениях можно пренебречь
по уравнению (10) с учетом значений констант (12). При вычислениях можно пренебречь ![]() по сравнению с радиусом цилиндрической полости
по сравнению с радиусом цилиндрической полости ![]() . Максимальное значение поперечного смещения в относительных единицах составляет приблизительно:
. Максимальное значение поперечного смещения в относительных единицах составляет приблизительно: 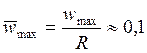 , максимальное значение изгибающего момента
, максимальное значение изгибающего момента  . Хотя значения перемещений велики, они, так же как и размер зоны отслоения получаются близкими к найденным в работе [5], где применялся численный метод для нелинейных задач. Поэтому данное решение может быть использовано в качестве первого приближения.
. Хотя значения перемещений велики, они, так же как и размер зоны отслоения получаются близкими к найденным в работе [5], где применялся численный метод для нелинейных задач. Поэтому данное решение может быть использовано в качестве первого приближения.
Перемещения на прилегающем участке
Оценим так же величину продольного смещения ![]() на свободных кромках свернутой в цилиндр пластины. Используя первое уравнение из системы (8) и решение (10) уравнения (9) запишем:
на свободных кромках свернутой в цилиндр пластины. Используя первое уравнение из системы (8) и решение (10) уравнения (9) запишем:
 (15)
(15)
Где константы ![]() и
и ![]() определяются формулами (12). При интегрировании уравнения (15) появляется еще одна константа
определяются формулами (12). При интегрировании уравнения (15) появляется еще одна константа ![]() , которая должна быть определена из граничных условий на отслоенном участке. Учитывая, что наше решение является приближенным, пренебрежем продольным перемещением на прилегающем участке BC и примем в качестве граничного условия
, которая должна быть определена из граничных условий на отслоенном участке. Учитывая, что наше решение является приближенным, пренебрежем продольным перемещением на прилегающем участке BC и примем в качестве граничного условия ![]() . После интегрирования и удовлетворения граничному условию получим
. После интегрирования и удовлетворения граничному условию получим ![]() :
:
 (16)
(16)
Подставим в (16) значения констант ![]() ,
, ![]() и упростим конечное выражение при
и упростим конечное выражение при ![]() , полагая
, полагая ![]() :
:
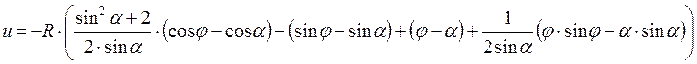 (17)
(17)
На свободной кромке пластины для значения угла отслоения ![]() получаем
получаем
 (18)
(18)
При таких перемещениях свободные кромки пластины будут наползать друг на друга (что фактически имеет место при сворачивании конвейерной ленты), если рассмотреть не пластину, а тонкую проволоку, сворачиваемую в кольцо, то будет наблюдаться перехлест концов проволоки. Условия, при которых реализуется решение данной задачи, можно выполнить, если взять ширину пластины ![]() , учитывая (18),
, учитывая (18), ![]() .
.
Оценим теперь величины перемещений на прилегающем участке BC. Здесь продольная сила и изгибающий момент (2) после подстановки контактных сил (3) будут:
 (19)
(19)
Подставляя в уравнения (6), связывающие усилия и перемещения при изгибе цилиндрической оболочки в одном направлении получим систему из двух дифференциальных уравнений для перемещений в зоне прилегания, аналогичную системе (8) для зоны отслоения:
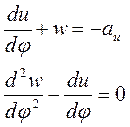 (20)
(20)
Система содержит очевидное противоречие с исходным предпосылками, принятыми при решении задачи. В силу прилегания пластины к поверхности цилиндра на участке BC должно быть ![]() и, как отмечалось выше, в рамках классической теории изгиба при чистом изгибе
и, как отмечалось выше, в рамках классической теории изгиба при чистом изгибе ![]() . Ясно, что для правомерности приведенного выше решения, перемещения, полученные из (20) должны быть малыми. Решая систему уравнений в той же последовательности, что и (8), при граничных условиях
. Ясно, что для правомерности приведенного выше решения, перемещения, полученные из (20) должны быть малыми. Решая систему уравнений в той же последовательности, что и (8), при граничных условиях
![]() ,
,  ,
, ![]() (21)
(21)
получим значения перемещений в зоне прилегания
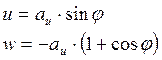 (22)
(22)
Таким образом, в зоне прилегания перемещения оказываются малыми порядка ![]() , в то время как, на отслоенном участке большими – порядка
, в то время как, на отслоенном участке большими – порядка ![]() . Видно, что предположение о плотном прилегании на участке BC выполняется приближенно.
. Видно, что предположение о плотном прилегании на участке BC выполняется приближенно.
Выводы
1. В статье получено решение контактной задачи о пластине, свернутой в цилиндр и помещенной в цилиндрическую полость, причем в отличие от известных решений [1,2] размер зоны прилегания заранее неизвестен и определяется в ходе решения.
2. Известно [7], что обычно принимаемое в подобных задачах распределение сил [3], противоречит (при использовании классической теории изгиба) предположению о чистом изгибе части пластины, плотно прилегающей к поверхности цилиндра. В данной статье показано, что это противоречие дает перемещения в зоне прилегания порядка 0,1 от толщины пластины.
3. Распространение полученного решения, учитывающего наличие зоны отслоения, на ортотропные пластины [1,2] не представляет сложности и требует только коррекции параметров в уравнениях (6), связывающих перемещения с внутренними силовыми факторами.
Список литературы
1. Черненко В.Д. Изгиб ортотропной цилиндрической пластины в цилиндрическую оболочку // Прикладная механика. 1972. Т. 15, № 4. С. 49-53.
2. Черненко В.Д. Расчет средств непрерывного транспорта. СПб.: Политехника, 2008. 386 с.
3. Моссаковский В.И., Гудрамович В.С., Макеев Е.М. Контактные задачи теории пластин и оболочек. М.: Машиностроение, 1978. 248 с.
4. Бидерман В.Л., Бояршинов С.В. Расчет храпового механизма пружинного типа // Труды кафедры сопротивления материалов МВТУ им. Н.Э. Баумана, 1947. C. 127-142.
5. Дмитриев С.Н., Солодовникова С.Ю. Нелинейная контактная задача об изгибе тонкой пластины, помещенной в цилиндрическую полость // Ракетно-космическая техника: фундаментальные и прикладные проблемы : труды 2-й Междунар. науч. конф. (Москва, 18-21 ноября 2003 г.) : в 4 ч. 2005. Ч. 2. С. 56.
6. Дмитриев С.Н., Солодовникова С.Ю. Контактная задача о равновесии пластины, свернутой в цилиндр // Аэрокосмические технологии, 2004-2007 : сб. тр. М.: Изд. МГТУ им. Н.Э. Баумана, 2008. С. 348-351.
7. Феодосьев В.И. Избранные вопросы и задачи по сопротивлению материалов. М.: Наука, 1967. 376 с.
8. Погорелов В.И. Строительная механика тонкостенных конструкций. СПб.: БХВ-Петербург, 2007. 528 с.
Публикации с ключевыми словами: изгиб, пластина, оболочка, деформации
Публикации со словами: изгиб, пластина, оболочка, деформации
Смотри также:
- 77-30569/240531 Экспериментальные исследования эксплуатационных свойств различных типов порошковой проволоки
- Разработка конечно-элементных моделей автомобильных кресел с пассивными подголовниками, отвечающих требованиям пассивной безопасности
- 77-30569/240203 Способ редуцирования металлургической порошковой проволоки
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



