научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#5 Май 2005
В. В. Павлов, д-р техн. наук проф., МГТУ "Станкин"
Полихроматические графы в теории систем
Одним из основных аспектов моделирования сложных систем является отображение различных связей между элементами этих систем, для чего используется аппарат теории графов [1]. Однако традиционный математический аппарат теории графов [2] не содержит средств одновременного описания и состава и разнообразных свойств вершин и ребер графа, что сужает возможности моделирования реальных систем. Такие средства содержит аппарат полихроматических ПS-множеств и ПS-графов. Более детальные исследования структуры и операций над ПS-множествами [З, 4, 5] позволяют существенно расширить представления о свойствах ПG-графов и возможностях их использования при моделировании систем.
Состав IIG-графа
Обычным графом называется пара G = (А, С), состоящая из множества A вершин и множества C ребер, связанных отношением инцидентности [2]. Полихроматическим назовем граф ПG с унитарной раскраской F(G), вершины и/или ребра которого являются полихроматическими множествами
![]() (1)
(1)
![]() (2)
(2)
где A, С — множества вершин и ребер, рассматриваемых без
учета их раскраски; F(a),
F(c) — множества
различных персональных цветов всех вершин и ребер; F(A), F(C)
— множество унитарных цветов — унитарные раскраски ПSА
и ПSC; ![]() — булевы матрицы
персональных раскрасок отдельных вершин и ребер;
— булевы матрицы
персональных раскрасок отдельных вершин и ребер; ![]() — булевы матрицы персональных
цветов вершин и ребер, одноименных с унитарными цветами F(A), F(C);
— булевы матрицы персональных
цветов вершин и ребер, одноименных с унитарными цветами F(A), F(C);
![]() —
булевы матрицы вариантов тел, обеспечивающих существование унитарных цветов F(A), F(C). Унитарная раскраска F(G) ПG-графа
определяется раскрасками его вершин и ребер.
—
булевы матрицы вариантов тел, обеспечивающих существование унитарных цветов F(A), F(C). Унитарная раскраска F(G) ПG-графа
определяется раскрасками его вершин и ребер.
Обычное множество А можно принять как полихроматическое, но с пустым составом унитарных цветов и пустыми составами персональных цветов элементов:
![]() (3)
(3)
аналогично можно представить множество С в виде
![]() (4)
(4)
Поэтому любой ПG-граф представляется тройкой
![]()
Состав ПSА вершин в ПG - графе может соответствовать (1) или (3), а состав ПSC ребер может соответствовать (2) или (4). Поэтому ПG-граф может относиться к одному из следующих видов:
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Из (1)—(7) следует, что в любом ПG-графе существуют множества А и С, определяющие обычный граф G = (A, C), вершины и ребра которого бесцветны; этот граф называется бесцветным каркасом ПG-графа. Например, на рис. 1 приведены компоненты ПG-графа вида (5). Множество ПSA вершин этого ПG- графа представляет собой элементы производственной системы, а множество ПSC дуг характеризует возможные пути перемещения обрабатываемых деталей на производственном участке. Бесцветный каркас ПG-графа показан в виде обычного графа G = (A, C). Состав унитарных цветов, характеризующих виды обрабатываемых поверхностей и другие свойства заготовок и деталей,
F(G) = (F1, F2, F3, F4, F5, F6, F7, F8, F9, Fl0, F11, F12)
является объединением унитарных цветов вершин F(A) и дуг F(C).
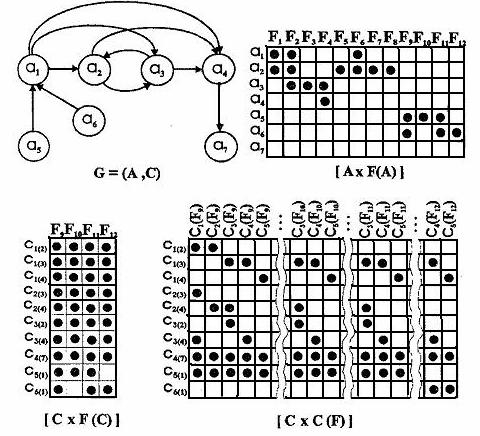
Рис. 1. ПG-граф структурной модели производственного участка:
Вершины ПG-графа: a1 — горизонтально-фрезерный станок; a2 — вертикально-фрезерный станок; a3 — токарный станок; а4 — сверлильный станок; а5 — рабочий; a6 — промышленный робот; а7 — склад деталей.
Цвета ПG-графа — свойства заготовок и деталей: F1 — плоская поверхность; F2 — торец; F3 — наружная поверхность вращения; F4 — круглое отверстие; F5 — фасонная поверхность; F6 — паз прямолинейный сквозной; F7 — паз прямолинейный глухой; F8 — паз криволинейный; F9 — перемещение заготовки (детали); F10 — нежесткая деталь; F11 — масса заготовки Р ≤ 15кг; F12 — масса заготовки 15 < Р ≤ 50кг; • — элемент булевой матрицы cp(q) = 1
Унитарная раскраска ПG-графа
Унитарная раскраска ПG-графа зависит как от раскрасок вершин и ребер, так и от взаимосвязи цветов вершин и ребер по условиям их существования. Возможны два вида такой взаимосвязи:
· условия существования унитарных цветов вершин не зависят от цветов ребер и, наоборот, условия существования унитарных цветов ребер на зависят от цветов вершин;
· условия существования унитарных цветов вершин зависят от цветов ребер и/или условия существования унитарных цветов ребер зависят от цветов вершин.
В реальных системах первому случаю соответствует ситуация, когда элементы системы — вершины ПG-графа — являются функционально самостоятельными объектами, свойства которых не зависят от других объектов и связей между ними. Примером является структурная модель производственного участка (см. рис. 1). Второму случаю соответствует, например, структурная модель конструкции сборного изделия, в которой свойства сопряжений — ребер ПG-графа — зависят от свойств сопрягаемых деталей — вершин ПG-графа.
При первом виде взаимосвязи F(A), F(C) и F(G) унитарные цвета вершин F(A) и ребер F(C) определяются независимо друг от друга в множествах ПSA и ПSC. Методика определения унитарных цветов ПS-множества в зависимости от состава его элементов и их персональных цветов приведена в [3]. Взаимосвязь всех персональных цветов F(ai) элементов А и унитарных цветов F(A) множества ПSA по условиям их существования описывается булевой матрицей
![]() (8)
(8)
состав персональных цветов F(ai), непосредственно влияющих на существование унитарных цветов F(A), удобно представить в блочной булевой матрице
 (9)
(9)
Блок ![]() описывает
зависимость существования каждого унитарного цвета Fj(A) от существования других унитарных цветов; блок вида
описывает
зависимость существования каждого унитарного цвета Fj(A) от существования других унитарных цветов; блок вида ![]() описывает
зависимость существования каждого унитарного цвета от существования
определенных персональных цветов элемента ai ПSA-множества.
Зависимость существования Fj(A) от персональных цветов элементов ПSA-множества описывается логическим уравнением
дизъюнктивной нормальной формы
описывает
зависимость существования каждого унитарного цвета от существования
определенных персональных цветов элемента ai ПSA-множества.
Зависимость существования Fj(A) от персональных цветов элементов ПSA-множества описывается логическим уравнением
дизъюнктивной нормальной формы
 (10)
(10)
Персональному цвету Fjk(aik) элемента aik, влияющему на существование Fj(A), соответствует равный единице элемент j-го столбца булевой матрицы (9), расположенный в jk-й строке, принадлежащей персональным цветам F(aik). Если существование Fj(A) зависит только от персональных цветов, входящих в (10), условие существования имеет вид
 (11)
(11)
Состав персональных цветов ребер, влияющих на существование унитарных цветов F(C), описывается аналогичной (9) булевой матрицей
![]() (12)
(12)
а зависимость существования Fj(C) от персональных цветов ребер описывается аналогичным (10) уравнением
![]() (13)
(13)
С помощью булевой матрицы (9) и вычисления условий вида (11) определяется состав F(A) унитарных цветов вершин ПSA. Аналогично и независимо от F(A) определяется состав F(C) унитарных цветов ребер ПS. Унитарная раскраска ПG-графа в этом случае определяется с помощью операций над F(A) и F(C), например,
![]() (14)
(14)
![]() (15)
(15)
и других. В логической форме, при представлении всех цветов в едином булевом векторном пространстве [3], соотношения (9), (10) имеют вид
![]() (16)
(16)
![]() (17)
(17)
Известно, что взаимосвязь персональных и унитарных цветов ПS-множества может иметь дизъюнктивную или конъюнктивную форму [3]; соответственно множества (1) и (2) могут быть дизъюнктивными или конъюнктивными. При описании ПSA и ПSC составы их компонент могут быть представлены как полными наборами (1), (2), так и сокращенными наборами [4]; минимальными наборами компонент дизъюнктивных множеств будут
![]() (18)
(18)
![]() (19)
(19)
а минимальными наборами компонент конъюнктивных множеств будут
![]() (20)
(20)
![]() (21)
(21)
Состав (5), (6) или (7) ПG-графа с учетом форм взаимосвязи персональных и унитарных цветов вершин и ребер, а также отношений (16), (17) определяется по схеме
 (22)
(22)
При втором виде взаимосвязи F(A), F(C)
и F(G), когда
унитарные цвета вершин и ребер взаимозависимы по условиям существования, состав
F(A) унитарных
цветов ПSA-множества вершин
определяется в зависимости от персональных цветов и вершин и ребер, инцидентных
этим вершинам. Поэтому булева матрица (9) дополняется блоками вида ![]() , описывающими
зависимость существования унитарных цветов F(A) от персональных цветов ребра ci ПSA-множества,
и матрица принимает вид
, описывающими
зависимость существования унитарных цветов F(A) от персональных цветов ребра ci ПSA-множества,
и матрица принимает вид
![]() (23)
(23)
Операции над ПG-графами
При выполнении операций над ПG-графами возникает проблема идентификации вершин и ребер в целях выявления их эквивалентности, поскольку эквивалентные элементы, в силу закона идемпотентности [6], при теоретико-множественных и логических операциях поглощаются друг другом. Эквивалентность элементов ПS-множеств рассмотрена в [5]. В операциях над ПS-графами проблема эквивалентности должна решаться и для вершин, и для ребер. При моделировании реальных систем эквивалентность вершин и ребер будет относительным понятием, зависящим от их влияния на определенные свойства системы, описываемые унитарными цветами ПG-графа. Условия эквивалентности вершин ai, aj, как элементов ПSA-множества [5], устанавливаются достаточно строгими:
 (28)
(28)
или менее строгими:
![]() (29)
(29)
Иногда условия эквивалентности устанавливаются с учетом не всего состава
цветов F(ai),
F(cj),
а лишь определенной группы цветов ![]() :
:
![]() (30)
(30)
Эквивалентность ребер сi, cj ПG-графов может определяться аналогичными условиями:
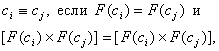 (31)
(31)
или
![]() (32)
(32)
или
![]() (33)
(33)
Если раскраски вершин и ребер взаимно независимы по условиях их существования, то условия эквивалентности вершин и ребер могут быть различными.
Наиболее простыми являются операции изменения состава исходного ПG-графа за счет исключения отдельных вершин и ребер.
Исключая вершину aj из ПSA, исключают ее из A,
а также исключают соответствующую строку из матриц ![]() и
и ![]() ; при этом могут
измениться составы цветов F(a),
F(A) и тел A(F). Если в исходном
графе существовало ребро cij, то это
ребро исключается из состава ПSC,
так как оно лишается второй инцидентной вершины. Аналогично поступают при
исключении ребра из ПSC,,
однако вершину, оставшуюся без инцидентного ребра, удаляют из ПSA только в случае, если это специально
оговорено в условиях задачи.
; при этом могут
измениться составы цветов F(a),
F(A) и тел A(F). Если в исходном
графе существовало ребро cij, то это
ребро исключается из состава ПSC,
так как оно лишается второй инцидентной вершины. Аналогично поступают при
исключении ребра из ПSC,,
однако вершину, оставшуюся без инцидентного ребра, удаляют из ПSA только в случае, если это специально
оговорено в условиях задачи.
Зависимость существования унитарного цвета Fj(A) от персональных цветов вершин и ребер описывается в этом случае не (10), а логическим уравнением
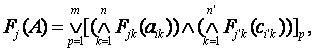 (24)
(24)
где n' — число ребер, персональные цвета которых влияют на существование Fj(A).
Аналогичным способом определяется состав унитарных цветов F(C) ПSC-множества
ребер в зависимости от персональных цветов и ребер и вершин, инцидентных этим
ребрам. Для этого булева матрица (12) дополняется блоками вида ![]() , описывающими
зависимость существования унитарных цветов F(C) ребер от персональных цветов вершин ai ПSA-множества:
, описывающими
зависимость существования унитарных цветов F(C) ребер от персональных цветов вершин ai ПSA-множества:
![]() (25)
(25)
Зависимость существования Fj(C) от персональных цветов и вершин и ребер описывается логическим уравнением (13), дополненным конъюнкцией персональных цветов Fj’k(ai’k) вершин, влияющих на существование Fj(C):
 (26)
(26)
Несмотря на внешнее сходство формул (24) и (26), их содержание может быть различным, поскольку они относятся к принципиально разным объектам системы — ее элементам и связям между элементами.
После определения унитарных цветов Fj(A) по матрице (9), а унитарных цветов Fj(C) — по матрице (25) унитарная раскраска F(G) ПG-графа в некоторых случаях может определяться так же, как в первом случае, по формулам вида (16), (17), и состав ПG-графа определяется по схеме (22). Следует иметь в виду, что использование формул (16), (17) предполагает определенную независимость унитарных цветов вершин и ребер по их влиянию на унитарную раскраску ПG-графа. Более общим является случай, когда такая независимость отсутствует и унитарная раскраска F(G) определяется по булевой матрице

![]() (27)
(27)
отражающей все формы взаимосвязи унитарных цветов вершин, ребер и ПG-графа в целом по условиям их существования. В этом случае матрица (27) должна входить в состав компонентов ПG-графа.
При добавлении новой вершины ak
вначале проверяется условие ее эквивалентности другим вершинам ПSA: если существует aj
= ak, то добавление ak не имеет смысла, так как в силу закона
идемпотентности она будет поглощена aj,
и состав ПSA не изменится.
Поэтому следует брать вершину, не эквивалентную ни одной из вершин в ПSA. Однако при моделировании реальных систем в
некоторых случаях необходимо иметь эквивалентные по своим свойствам элементы —
например, с целью резервирования или дублирования для повышения надежности
системы. В таких случаях эквивалентному элементу ak
формально присваивается новое свойство Fq
— быть "резервным", "дублирующим" и т. п., и это свойство
включается как новый цвет в F(ak), после чего ak
уже не будет эквивалентным aj по
условию (29) или (28). После добавления ak
в матрицах ![]() и
и
![]() добавляется
новая строка, соответствующая ak.
Если при этом
добавляется
новая строка, соответствующая ak.
Если при этом ![]() , то изменится состав F(a) за счет добавления
новых персональных цветов и, возможно, появятся новые тела в A(F) и новые унитарные
цвета в F(A).
Введение ak в ПSA требует также решения вопроса о появлении
новых связей между элементами исходного множества вершин и ak,
т. е. о добавлении нового ребра или нескольких ребер. Добавление нового ребра cjk в состав ребер исходного ПG-графа осуществляют по методике, аналогичной добавлению
новой вершины; однако следует иметь в виду, что добавить ребро cjk можно только в случае, если в ПSA существуют вершины aj,
ak, которые будут инцидентными
вершинам этого ребра.
, то изменится состав F(a) за счет добавления
новых персональных цветов и, возможно, появятся новые тела в A(F) и новые унитарные
цвета в F(A).
Введение ak в ПSA требует также решения вопроса о появлении
новых связей между элементами исходного множества вершин и ak,
т. е. о добавлении нового ребра или нескольких ребер. Добавление нового ребра cjk в состав ребер исходного ПG-графа осуществляют по методике, аналогичной добавлению
новой вершины; однако следует иметь в виду, что добавить ребро cjk можно только в случае, если в ПSA существуют вершины aj,
ak, которые будут инцидентными
вершинам этого ребра.
Обосновать возможность добавления новой вершины или ребра в исходный ПG-граф чисто формальными средствами можно только в случае, если это следует из известного состава и условий существования унитарных цветов и персональных цветов всех вершин и ребер. В остальных случаях эта проблема решается методами искусственного интеллекта и поиска новых решений.
Простой является операция выделения части ПG-графа,
так как в ней участвуют вершины и ребра только одного, исходного ПG-графа. Известно [2], что частью обычного графа G = (А, С) называется граф Gi
= (Ai, Ci)
такой, что ![]() и
для каждого ребра
и
для каждого ребра ![]() в составе Ai
имеются обе инцидентные этому ребру вершины aj,
ak. Частью ПG-графа будет граф
в составе Ai
имеются обе инцидентные этому ребру вершины aj,
ak. Частью ПG-графа будет граф ![]() , бесцветный каркас Gi = (Ai,
Ci) которого является частью
каркаса G = (А, С) исходного ПG-графа. В выделяемой части ПGi
составы унитарных цветов
, бесцветный каркас Gi = (Ai,
Ci) которого является частью
каркаса G = (А, С) исходного ПG-графа. В выделяемой части ПGi
составы унитарных цветов
![]()
и условия
существования унитарных цветов в F(Gi), F(Ai), F(Ci) соответствуют условиям существования этих
цветов в исходном ПG-графе. Выделение ![]() осуществляется
по-разному в зависимости от условий задачи. Если в состав исходных данных
входят вершины или ребра искомой части ПG-графа,
то задача решается двумя путями.
осуществляется
по-разному в зависимости от условий задачи. Если в состав исходных данных
входят вершины или ребра искомой части ПG-графа,
то задача решается двумя путями.
1. Задается исходный ПG-граф и
состав ![]() вершин
искомого ПG-графа, а затем определяется
состав
вершин
искомого ПG-графа, а затем определяется
состав ![]() ребер,
инцидентные вершины которых входят в Аi,
и определяются унитарные цвета F(Ai), F(Ci), F(Gi). Способ определения унитарных цветов
зависит от условий их существования: если унитарные цвета вершин и ребер
существуют независимо друг от друга, то используются булевы матрицы вида (9),
(12) и формулы (10), (13); если унитарные цвета взаимозависимы по условиям их
существования, то используются булевы матрицы (23), (25) и, возможно, (27), а
также формулы (24), (26). В этом случае в ПGi
могут существовать изолированные вершины.
ребер,
инцидентные вершины которых входят в Аi,
и определяются унитарные цвета F(Ai), F(Ci), F(Gi). Способ определения унитарных цветов
зависит от условий их существования: если унитарные цвета вершин и ребер
существуют независимо друг от друга, то используются булевы матрицы вида (9),
(12) и формулы (10), (13); если унитарные цвета взаимозависимы по условиям их
существования, то используются булевы матрицы (23), (25) и, возможно, (27), а
также формулы (24), (26). В этом случае в ПGi
могут существовать изолированные вершины.
2. Задается исходный ПG-граф и
состав ![]() ребер
искомого ПG-графа, а затем определяется
состав
ребер
искомого ПG-графа, а затем определяется
состав ![]() вершин,
инцидентных заданным ребрам. Унитарные цвета F(Ai), F(Ci), F(Gi) определяются аналогично п. 1. В этом
случае в ПGi не будут
существовать изолированные вершины.
вершин,
инцидентных заданным ребрам. Унитарные цвета F(Ai), F(Ci), F(Gi) определяются аналогично п. 1. В этом
случае в ПGi не будут
существовать изолированные вершины.
Если в составе исходных данных указывается только унитарная раскраска F(Gi)
выделяемой части ![]() , то задача будет определенной,
только если в исходном ПG-графе
взаимосвязь между унитарными цветами соответствует (17), ибо в этом случае
имеет место
, то задача будет определенной,
только если в исходном ПG-графе
взаимосвязь между унитарными цветами соответствует (17), ибо в этом случае
имеет место ![]() , и условию задачи удовлетворяют
значения F(Ai)
= F(Ci)
= F(Gi).
Для определения состава вершин Ai
используются столбцы матрицы [А х F(A)], соответствующие унитарным цветам F(Ai); для
определения минимального набора вершин Ai
используется матрица [А х A(F)] вариантов тел, обеспечивающих существование унитарных
цветов F(Ai).
Состав ребер Ci выделяемой части ПG-графа определяется аналогично определению состава
вершин.
, и условию задачи удовлетворяют
значения F(Ai)
= F(Ci)
= F(Gi).
Для определения состава вершин Ai
используются столбцы матрицы [А х F(A)], соответствующие унитарным цветам F(Ai); для
определения минимального набора вершин Ai
используется матрица [А х A(F)] вариантов тел, обеспечивающих существование унитарных
цветов F(Ai).
Состав ребер Ci выделяемой части ПG-графа определяется аналогично определению состава
вершин.
Если взаимосвязь между унитарными цветами в исходном ПG-графе соответствует (16), то при задании в исходных данных требуемого состава F(Gi) унитарных цветов выделяемой части ПGi необходимо дополнительно указать либо желаемый состав F(Ai), либо F(Ci), после чего задача решается изложенными выше способами.
К операциям выделения части ПG-графа относится, например, построение маршрутов — цепей, циклов и т. п. Для этих частей обычного графа характерной является упорядоченная последовательность вершин и ребер, образующих маршрут [2]. Так, в графе G = (А, С) простой элементарный путь μi можно описать тремя способами:
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
Полагая, что G = (А, С) — бесцветный каркас ПG-графа, получим
![]() (37)
(37)
Рассмотрим построение путей в ПG-графе (см. рис. 1). В соответствии со схемой (22) этот граф имеет вид
![]()
Унитарная раскраска вершин F(A), дуг F(C) и пути в целом F(G) определяется так же, как при выделении части ПG-графа с независимыми условиями существования унитарных цветов вершин и ребер. Так, для пути

получим:
поскольку ![]() —
дизъюнктивное множество, то по матрице [А х F(A)] получим
—
дизъюнктивное множество, то по матрице [А х F(A)] получим
![]()
поскольку ![]() —
конъюнктивное множество, то по матрице [С x F(C)]
получим
—
конъюнктивное множество, то по матрице [С x F(C)]
получим
![]()
и по матрице [С x C(F)] определим состав тел, реализующих эти цвета:
C4(F9)=C4(F10)=C4(F11)=(c5(1), c1(3), c3(4), c4(7)).
Таким образом, унитарная раскраска части ПG-графа (см. рис. 1), соответствующей пути μi вычисляемая по формуле (16), равна
![]()
В отличие от операции выделения части ПG-графа, при вычислении разности, пересечения и объединения участвуют разные ПG-графы; кроме того, эти операции могут выполняться раздельно над множеством вершин и ребер исходных ПG-графов. Рассмотрим, например, исходные графы
![]()
Возможны следующие сочетания операций объединения, пересечения и разности множеств вершин и ребер этих ПG-графов:
 (38)
(38)
Таким образом, если операции объединения ПGiи ПGj соответствует
![]() (39)
(39)
операции пересечения соответствует
![]() (40)
(40)
операции разности соответствует
![]() (41)
(41)
то
![]() (42)
(42)
![]() (43)
(43)
и т. д. При выполнении операций над разными ПG-графами необходимо учитывать условия эквивалентности их вершин и ребер.
Если раскраски вершин и ребер в ПG-графах взаимно независимы по условиям их существования, то все виды операций из (38) над ПGi и ПGj выполняются раздельно над их множествами вершин и множествами ребер, как это, например, описывается в (39)—(43) и т. п. При этом следует иметь в виду, что операция над множествами ПSCi, ПSCj ребер должна выполняться после операции над множествами ПSAi, ПSAj вершин, и в состав ребер искомого ПG-графа включаются только те ребра, для которых имеются обе инцидентные вершины. Методы выполнения операций объединения, пересечения и разности ПS-множеств приведены в [5]. После операции над ПS-множествами вершин и ребер по формулам (14), (15) или (16), (17) определяется унитарная раскраска F(G) ПG-графа. Операции пересечения и разности графов ПGi и ПGj не вызывают особых трудностей, поскольку результатом их выполнения являются части исходных ПGi-графов. Действительно, при выполнении операции пересечения (40) получается часть исходного ПGi-графа, вершины и ребра которой эквивалентны вершинам и ребрам ПGj-графа; при выполнении операции разности (41) получается часть исходного ПGi-графа, вершины и ребра которой не эквивалентны вершинам и ребрам ПGj -графа. В обоих случаях на полученную часть вершин и ребер распространяются условия существования раскрасок исходного ПGi-графа. Рассмотрим, например, операции над ПG-графами (рис. 2, а, б):

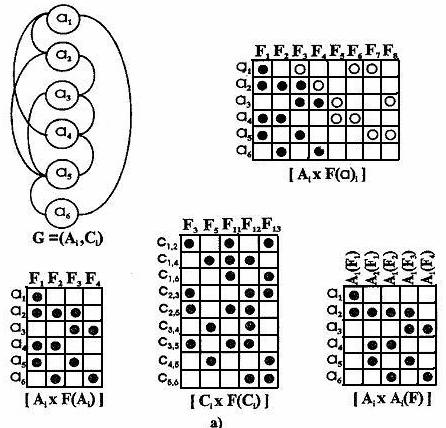

Рис. 2. Полихроматические графы ПGi(a) и ПGj(б):
• - cp(q) = 1 и ap входит в составы тел унитарного цвета Fq;
○ – cp(q) = 1, но ap не входят в сотавы тел унитарного цвета Fq
При
пересечении ![]() получается
часть ПGi’ с
составами вершин и ребер
получается
часть ПGi’ с
составами вершин и ребер
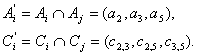
Исключая из булевых матриц (рис. 2, а) строки, соответствующие не вошедшим в пересечения вершинам и ребрам, получим новые матрицы и раскраски:

следовательно, унитарная раскраска части ПGi’, вычисляемая по формуле (14), равна
![]()
При разности ПGi \ ПGj получается часть ПGi” , в которой состав вершин равен
![]()
Состав ребер Сi”, вычисляемый как разность множеств Ci и Cj равен
![]()
однако только ребра c1,4 и c1,6 имеют обе инцидентные вершины — (a1, a4) и (a1, a6), поэтому
![]()
Раскраски компонентов ПGj” равны

поскольку в
матрице ![]() на
рис. 2, а нет ни одного тела, реализующего унитарные цвета F(Ai) при Ai”
= (a1, a4,
a6). Поэтому унитарная раскраска ПGi” равна
на
рис. 2, а нет ни одного тела, реализующего унитарные цвета F(Ai) при Ai”
= (a1, a4,
a6). Поэтому унитарная раскраска ПGi” равна
![]()
При разности ПGj\ПGi получается часть ПGj’ с составом вершин и ребер
![]()
ребра c2,8, c3,7 и c5,7 не входят в Cj’ из-за отсутствия второй инцидентной вершины. Раскраска этой части ПGj-графа (рис. 2, б) равны

Таким образом, при вьщелении части ПG-гpaфа, при вычислении пересечения или разности
ПGi ПGj в составах унитарных цветов вершин, ребер и
ПG-графа в целом не могут появиться новые
унитарные цвета, не существовавшие ранее в исходных составах F(A), F(C) и F(G). В отличие от этих операций, объединение ![]() ,
соответствующее (39), связано с возможностью появления новых унитарных цветов
из-за увеличения составов ПSA
и ПSС за счет новых вершин и
ребер. Примером объединения ПGi,
ПGj, показанных на рис. 2,
является ПG-граф (рис. 3). Булева матрица
,
соответствующее (39), связано с возможностью появления новых унитарных цветов
из-за увеличения составов ПSA
и ПSС за счет новых вершин и
ребер. Примером объединения ПGi,
ПGj, показанных на рис. 2,
является ПG-граф (рис. 3). Булева матрица
![]() этого
графа являются объединениями соответствующих матриц исходных графов (см. рис.
2). Из матрицы [А х A(F)] ПG-графа (рис.
3) следует, что здесь не только сохранились все тела унитарных цветов F(Ai) и F(Aj), но
дополнительно появились новые тела A1(F6) и A3(F3); кроме того, появились тела A1(F6),
A2(F6)
унитарного цвета F6(A), не существовавшего ранее в F(Ai) и F(Aj).
этого
графа являются объединениями соответствующих матриц исходных графов (см. рис.
2). Из матрицы [А х A(F)] ПG-графа (рис.
3) следует, что здесь не только сохранились все тела унитарных цветов F(Ai) и F(Aj), но
дополнительно появились новые тела A1(F6) и A3(F3); кроме того, появились тела A1(F6),
A2(F6)
унитарного цвета F6(A), не существовавшего ранее в F(Ai) и F(Aj).

Рис. 3. ПG-граф обьединения ПGi и ПGj:
• - cp(q) = 1 и ap входит в составы тел унитарного цвета Fq;
○ – cp(q) = 1, но ap не входят в сотавы тел унитарного цвета Fq
Из рассмотренных примеров следует, что при выполнении операций объединения, пересечения и разности графов ПGi, ПGj с независимыми условиями существования унитарных цветов вершин и ребер определение раскрасок F(A) и F(С) искомого ПG-графа осуществляется раздельно. Аналогично определяются раскраски вершин и ребер при выполнении комбинированных операций вида (42), (43) и т. п. Если условия существования унитарных цветов вершин и ребер исходных графов ПGi, ПGj взаимозависимы, то определение унитарных раскрасок F(A) и F(C) несколько усложняется, поскольку приходится использовать булевы матрицы (23), (26), однако это не вносит принципиальных трудностей. Аппарат полихроматических графов открывает широкие возможности структурного моделирования сложных систем и унификации математического обеспечения компьютерных технологий проектирования [7].
Список литературы
1. Технология системного моделирования /Е. Ф. Аврамчук, А. А, Вавилов, С. В. Емельянов и др.; Под общ. ред С. В. Емельянова и др. М.: Машиностроение; Берлин: Техник, 1988, 520 с.
2. Зыков А. А. Основы теории графов. М.: Наука, 1987. 384 с.
3. Павлов В. В. Полихроматические множества в теории систем. Структура ПS-множеств / Информационные технологии. 1997. № 7. С. 11-16.
4. Павлов В. В. Полихроматические множества в теории систем. Изменение состава ПS-множеств / Информационные технологии. 1998. № 1. С. 4—8.
5. Павлов В. В. Полихроматические множества в теории систем. Операции над ПS-множествами / Информационные технологии. 1998. № 3. С. 8—13.
6. Куратовский К., Мостовский А. Теория множеств. М.: Мир, 1970. 416 с.
7. САПР. Типовые математические модели объектов проектирования в машиностроении / Методические указания РД50—464—84. М.: Изд-во Стандартов, 1985, 202 с.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И СТРУКТУРНЫЙ СИНТЕЗ
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 6, 1998
Ключевые слова: Теория систем, моделирование, полихроматические графы, раскраска графа, операции над полихроматическими графами, логические матрицы.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



