научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2013
DOI: 10.7463/0113.0513571
УДК 61:004.62
Россия, МГТУ им. Н.Э. Баумана
Одним из проявлений целостности организма человека является синхронизация работы и взаимовлияние его отдельных подсистем. Поэтому всестороннее изучение феномена биосинхронизации представляется весьма актуальным и перспективным направлением, которое требует не только соответствующей технической оснащенности, но и математических методов обработки сигналов, моделирования органов и систем организма. Ниже предложен подход к исследованию взаимосвязей в сердечно-сосудистой системе.
1. Актуальность задачи исследования взаимосвязей в сложных биосистемах
Принцип синхронизации в рассматриваемом случае означает то, что все подсистемы организма, составляя единое целое, влияют на состояние друг друга посредством существующих взаимосвязей. Изменение характеристик взаимосвязей обусловливается адаптационными реакциями организма и является, по мнению многих авторов, одним из наиболее ранних признаков нарушения устойчивости организма.
С количественной точки зрения синхронное взаимодействие можно оценить различными параметрами, например, коэффициентами связи, оценками степени организации (упорядоченности) взаимодействующих подсистем и др., которые могут быть определены из анализа биосигналов. Однако наиболее информативным представляется анализ взаимосвязей на основе математических моделей исследуемых подсистем.
Биосистемы имеют сложную, пространственно распределенную структуру. Классические методы идентификации таких систем, основанные на детальном анализе каждой составляющей, приводят к громоздким математическим моделям, которые трудно интерпретировать. Однако есть случаи, когда система, которая выглядит очень сложной на микроскопическом уровне, адекватно описывается простыми уравнениями с сосредоточенными параметрами на макроскопическом уровне, который отражает коллективное поведение всех составляющих исследуемой системы [1-3]. В этом отношении представляет наибольший интерес теоретическая возможность идентификации или реконструкции уравнений динамики подсистем организма на макроуровне по характеристикам отдельных биологических сигналов или их совокупности.
Известны методы подобной реконструкции, основанные на работах Р. Такенса, С. Осовского и других [4, 5]. Методы вложения Такенса и нейроидентификации отличаются универсальностью и позволяют строить информационные модели динамических систем. Однако эти модели, описывая «вход-выход», не отражают структуру исследуемой системы, не содержат физиологически обусловленных параметров.
Перспективным представляется метод идентификации сложных систем, основанный на концепции модельных уравнений [6-8]. В основе концепции лежит положение о том, что небольшое число сравнительно простых математических моделей дает ключ к пониманию и исследованию огромного количества различных явлений. Суть заключается в том, что априори предполагается, что, во-первых, имеются характерные типы движения, свойственные системам различной физической природы. Во-вторых, все физическое многообразие может быть представлено в форме достаточно простых модельных уравнений. Например, широко распространенное колебательное движение различных систем может быть описано уравнением Ван-дер-Поля. Такие базовые модели в отдельности хорошо изучены, их параметры имеют физическую интерпретацию, что позволяет строить на их основе модели сложных систем различной физической природы [8].
В данной работе на примере исследования сердечно-сосудистой системы, предлагается метод идентификации, основанный на сочетании базовых и информационных моделей.
2. Разработка модели пульсовой активности
Впервые принципы синергетики при описании сердечно-сосудистой системы были использованы А. Стефановской [2, 9]. В указанных работах исходили из того, что организм человека, как любая сложная система естественного происхождения, имеет очень много степеней свободы. В процессе естественной эволюции выделяются несколько главных степеней, к которым подстраиваются все остальные. Динамика ограниченного числа параметров, представленная дифференциальными уравнениями второго порядка, в форме отражает основные свойства исследуемой биосистемы.
Однако предложенные однотипные модели динамики сердца, легких и сосудов носят информационный характер и не содержат физиологически обусловленных параметров, что затрудняет их использование в диагностических целях. Кроме того, в предложенных моделях взаимосвязи представлены в простейшей форме пропорциональной зависимости.
Основываясь на концепции базовых моделей, построим модель пульсового механизма по результатам изменения перемещения стенок артериального сосуда. Полученное модельное уравнение может быть использовано для моделирования взаимосвязанных подсистем, например, сердца и сосудистой системы, с целью установления новых причинно-следственных связей. Для успешного проведения процесса реконструкции необходимо максимально использовать априорную информацию об исследуемой системе с целью задания структуры модели и выбора вида нелинейной функции. Одна из особенностей функционирования исследуемой системы заключается в том, что она функционирует в режиме устойчивых колебаний. Другая особенность обусловлена инерционными свойствами колеблющихся материальных объектов. Известно, что с ростом частоты амплитуда колебаний падает. Предположим, что для рассматриваемой задачи идентификации пульсового механизма априорных знаний об особенностях функционирования исследуемой системы достаточно. В более сложных случаях необходимо учитывать и другие особенности.
В качестве модельного уравнения, описывающего предельные циклы, выберем нелинейное уравнение, слагаемые которого в рассматриваемой задаче имеют наглядный физический смысл:
![]() (1)
(1)
В уравнении (1) обозначено: ![]() – ускорение стенки артерии,
– ускорение стенки артерии, ![]() – ее скорость,
– ее скорость,
![]() - перемещение,
- перемещение, ![]() - частота основного гармонического колебания, F(X) – коэффициент затухания осциллятора, где X – вектор возможных аргументов функции. В рассматриваемом случае F(X) зависит от состояния сосудистой системы (упругости стенок, вязкости крови и др. факторов).
- частота основного гармонического колебания, F(X) – коэффициент затухания осциллятора, где X – вектор возможных аргументов функции. В рассматриваемом случае F(X) зависит от состояния сосудистой системы (упругости стенок, вязкости крови и др. факторов).
Из этого уравнения, задав соответствующий вид функции F(X) можно получить различные модельные уравнения, например Ван-дер-Поля или Релея.
Выбор нелинейной функции F(X) – задача не тривиальная. Здесь возможны разные подходы. Например, функцию F(X) можно аппроксимировать с помощью методов искусственного интеллекта, например, с использованием нейросетевых методов. Такой подход применяется, если неизвестны или известны не полностью законы функционирования системы. В данной работе рассмотрим аппроксимацию функции F(X) исходя из законов и особенностей функционирования системы и методов реализации этих особенностей в модельных уравнениях.
Известно несколько уравнений, позволяющих математически описать предельные циклы. Наиболее часто используется уравнение Ван-дер-Поля. Это уравнение содержит одну переменную ![]() , которая в нашем случае определяет перемещение стенки кровеносного сосуда. Оно имеет следующий вид:
, которая в нашем случае определяет перемещение стенки кровеносного сосуда. Оно имеет следующий вид:
![]() (2)
(2)
Уравнение (2) в принципе позволяет получить режим предельного цикла. Однако из теории нелинейных колебаний известно, что при данном виде среднего члена амплитуда колебаний не зависит от частоты. Такой вывод противоречит физике рассматриваемого процесса, поскольку инерционность стенки обязательно будет приводить к уменьшению амплитуды с ростом частоты.
Для устранения этого несоответствия рассмотрим уравнение Релея, которое имеет вид:
![]() (3)
(3)
В данном случае амплитуда убывает с возрастанием частоты ![]() .
.
Исходя из анализа уравнений (2) и (3), представим нелинейную функцию F(X) уравнения (1) в виде комбинации членов, описывающих затухание в уравнениях Ван-дер-Поля и Релея:
![]()
Полученное уравнение не учитывает влияния сердечной подсистемы, так как взаимодействие подсистем традиционно описывается правыми частями модельных уравнений. Поэтому, поскольку стенки сосуда перемещаются под действием давления тока крови, то это давление в первом приближении можно представить функцией ![]() . Несмотря на простой вид, такая модель описывает изменение давления под действием прямой и отраженной волн тока крови.
. Несмотря на простой вид, такая модель описывает изменение давления под действием прямой и отраженной волн тока крови.
Окончательно модельное уравнение имеет вид:
![]() (4)
(4)
Исходной информацией для определения неизвестных параметров управления является временной ряд пульсаций стенки сосуда (пульсограмма). Данные временного ряда предварительно обрабатываются с целью удаления тренда, стабилизации частоты, уменьшения шума.
Учитывая, что система функционирует в режиме предельного цикла, неизвестные параметры ω0 и r уравнения (4) находятся из экспериментальных данных. После их определения, используя измерительные значения ![]() и вычисленные значения
и вычисленные значения ![]() и
и ![]() , методом наименьших квадратов находятся значения P,
, методом наименьших квадратов находятся значения P, ![]() , ε1, и ε1. Здесь i=1, …, N, и N – длина временного ряда.
, ε1, и ε1. Здесь i=1, …, N, и N – длина временного ряда.
Пример реализации пульсового сигнала исследуемой системы приведен на рис. 1.

Рис. 1. Пульсовой сигнал
Для получения временных рядов ускорения и скорости перемещения стенки сосуда можно применить численное дифференцирование исходного временного ряда (перемещение стенки сосуда) на основе полиноминальной аппроксимации. Однако в данном случае использование преобразования Фурье позволило аналитически рассчитать производные для пульсового сигнала. Графики первой и второй производной сигнала показаны соответственно на рис. 2 и рис. 3.

Рис. 2. График первой производной

Рис. 3. График второй производной
Используя временные реализации на рис. 1-3, были получены следующие параметры модели: ω0=6.125 и r=0.065, P=29.5, ![]() =36.15, ε1=-0.3 и ε2=-3.37·105.
=36.15, ε1=-0.3 и ε2=-3.37·105.
Выходные сигналы объекта и модели приведены на рис. 4, а их фазовые портреты на рис. 5.
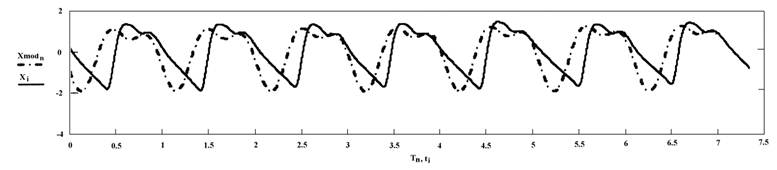
Рис. 4. Результаты моделирования
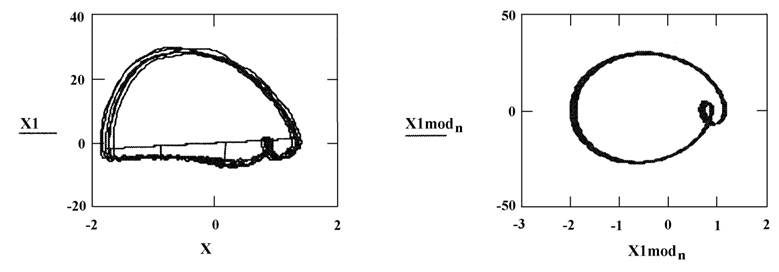
Рис. 5. Фазовые портреты
3. Выбор и исследование функций связи «сердце-сосуды»
Система кровоснабжения человека представляет собой сложный механизм, оценить состояние которого мы попытаемся, наблюдая ограниченное число сигналов в форме временного ряда. В абсолютном большинстве случаев в качестве переменного ряда для такой оценки используются электрокардиограмма (ЭКГ) или фонограмма (ФГ). Отметим, что ЭКГ отражает только электрическую активность сердечной мышцы, в то время как гораздо важнее оценить функциональную способность сердца в качестве насоса. Оценка этих способностей производится по ЭКГ косвенными способами. Напротив, фонограмма больше несет информации о механике сердечной мышцы.
Другим доступным для измерения сигналом является сигнал пульсовой волны (СПВ). Этот сигнал отражает, прежде всего, механические свойства сосудистой системы. Используемые в настоящее время методы обработки ЭКГ, ФГ и СПВ основаны на стандартных алгоритмах анализа временных рядов и экспертных методах обработки образов. Следует подчеркнуть, что сигналы обрабатываются совершенно независимо друг от друга. Вместе с тем представляется весьма актуальной и многообещающей задача совместной обработки этих сигналов, поскольку каждый из них описывает разные свойства взаимосвязанных подсистем сердечно-сосудистой системы.
В общем случае модель взаимосвязи двух подсистем включает модели самих подсистем и функционалы, описывающие их взаимосвязи:
![]()
![]()
Функционалы I12 и I21, стоящие в правых частях системы, описывают механизмы взаимодействия подсистем, ![]() - вектор фазовых переменных. При определении вида функционалов I12 и I21 будем исходить из ранее сформулированной гипотезы: несмотря на то, что взаимосвязи в биосистемах весьма разнотипные и многоуровневые, имеются основные, которые и задают параметры синхронного поведения. Эти взаимосвязи могут быть описаны простыми моделями.
- вектор фазовых переменных. При определении вида функционалов I12 и I21 будем исходить из ранее сформулированной гипотезы: несмотря на то, что взаимосвязи в биосистемах весьма разнотипные и многоуровневые, имеются основные, которые и задают параметры синхронного поведения. Эти взаимосвязи могут быть описаны простыми моделями.
Рассмотрим простой случай, когда подсистема сердца представлена не структурно-функциональной моделью, а ее выходным сигналом e(t), сигналом ЭКГ. Тогда модель взаимодействия двух подсистем можно представить в виде:
![]() (5)
(5)
Проведем исследование разных подходов к формированию функций взаимосвязи с использованием синхронно зарегистрированных сигналов. В частности, исследуем подход на основе физических представлений о взаимодействии двух связанных колебательных систем, в соответствии с которым функция взаимосвязи представляется в виде следующего выражения:
![]() (6)
(6)
Где ![]() - перемещение стенки кровеносного сосуда, е – электрокардиосинал (электрическая активность сердца). Неизвестные параметры α и β определяются методом наименьших квадратов на этапе параметрической идентификации модели подсистемы.
- перемещение стенки кровеносного сосуда, е – электрокардиосинал (электрическая активность сердца). Неизвестные параметры α и β определяются методом наименьших квадратов на этапе параметрической идентификации модели подсистемы.
Учет функции взаимосвязи в виде выражения (6) приводит к результатам моделирования пульсовой активности, приведенных на рис. 6 и 7.

Рис. 6. Учет воздействия сердечной подсистемы на пульсовую подсистему

Рис. 7. Фазовые портреты исходной системы и модельной системы
Из анализа рисунков видно, что такой подход к описанию функции взаимодействия является упрощенным. Для описания взаимодействия связанных подсистем со сложной реакцией на выходе необходимо использовать аппроксимации функции связи с большим количеством коэффициентов. Это в свою очередь обеспечит большие адаптационные возможности уравнений связи.
4. Идентификация связи на нейронной сети Вольтерра
Идентификацию связи между исследуемыми подсистемами проведем, используя информационные модели в форме нейронной сети Вольтерра. Эта динамическая сеть позволяет производить нелинейную обработку последовательности сигналов e(t), задержанных относительно друг друга. Исследуем нейросетевую аппроксимацию неизвестной функции взаимосвязи с помощью сети Вольтерра ![]() , где yn– выходной сигнал сети Вольтерра в момент tn.
, где yn– выходной сигнал сети Вольтерра в момент tn.
Возбуждением для сети в момент tn служит входной вектор
![]() , где L – количество единичных задержек, а (L+1) означает длину вектора. Сеть генерирует в соответствии с выражением
, где L – количество единичных задержек, а (L+1) означает длину вектора. Сеть генерирует в соответствии с выражением
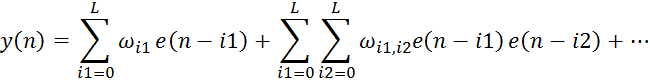
![]() , (7)
, (7)
где веса ωi, ωij, ωijk и т.д., называемые ядрами Вольтерра [5], соответствуют реакциям высших порядков. Нелинейная функциональная зависимость выходного сигнала сети ynот входного сигнала е является естественным полиномиальным обобщением описания линейного фильтра.
При адаптации реакции системы Вольтерра к заданной последовательности значений определим целевую функцию как
![]() .
.
Легко показать, что при ограничении в разложении K=3 значения межнейронных связей определяются из решения дифференциальных уравнений

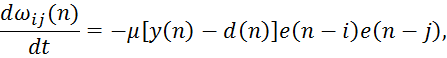

для i, j, l=1,2,…, L.
Для упрощения структуры сети (7) и уменьшения ее вычислительной сложности разложение Вольтерра можно представить в следующей форме:
![]() , (8)
, (8)
где используются обозначения yn=y(n), en=e(n-i) и т.д. Выражение (8) описывает динамическую нейронную сеть с полиномиальной нелинейностью. Подбор весов с помощью алгоритма обратного распространения ошибки производится последовательно слой за слоем.
Применим сеть Вольтерра для аппроксимации неизвестной функции взаимосвязи в уравнении
![]() ,
,
где ![]() – сигнал пульсовой волны; Fсвязи – функция взаимосвязи, описывающая воздействие сердца на сосуды.
– сигнал пульсовой волны; Fсвязи – функция взаимосвязи, описывающая воздействие сердца на сосуды.
В экспериментальных исследованиях используется принцип естественной симметрии ядер Вольтерра, вследствие которой все веса ωi1, ωi2,…,iK имеют одни и те же значения для каждой комбинации индексов i1, i2,…, iK. Тогда, например, для L=2 и K=3 можно записать следующее дифференциальное уравнение, описывающее функционирование сети Вольтерра:
![]()
![]() , (9)
, (9)
где е – сигнал электрической активности сердца, зарегистрированный синхронно с сигналом пульсовой волны.
Неизвестные параметры ![]() , определяемые в процессе обучения сети с использованием известных значений электрической активности сердца и требуемого значения выхода сети, соответствуют следующим ядрам Вольтерра:
, определяемые в процессе обучения сети с использованием известных значений электрической активности сердца и требуемого значения выхода сети, соответствуют следующим ядрам Вольтерра:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
В процессе обучения для нейронной сети Вольтерра, описываемой выражением (9), были получены следующие значения коэффициентов:
ω0=-7.832;
ω1=43.584;
ω01= ω10=564.5;
ω00=53.144;
ω11=5.222·10-2;188222·10-3;
ω001= ω100= ω010=3.324.
Полученная модель сердечно-сосудистой системы является комбинацией модельного уравнения Ван-дер-Поля - Релея и информационной модели в форме сети Вольтерра. Модельное уравнение содержит физиологически обусловленные параметры, а информационная модель адекватно представляет сложные нелинейные связи между рассматриваемыми подсистемами. Параметры полученной комбинированной модели могут служить характеристическими признаками при решении задач диагностики.
Список литературы
1. Haken H. Cooperative phenomena in systems far from thermal equilibrium and in nonphysical systems // Rev. Mod. Phys. – 1975. - Vol. 47, no. 1. - P. 67-121.
2. Reversible transitions between synchronization states of the cardiorespiratory system / A. Stefanovska, H. Haken, M. Hozic, et al. // Phys. Rev. Lett. – 2000. - Vol. 85, no. 22. - P. 4831-4834.
3. Mette S., Olufsen Ali Nadim. On deriving lumped models for blood flow and pressure in the systemic arteries // Mathematical biosciences and engineering. - 2004. - Vol. 1, no. 1. - P.61-80.
4. Анищенко В.С., Вадивасова Т.Е., Астахов В.В. Нелинейная динамика хаотических и стохастических систем. Фундаментальные основы и избранные проблемы. - Саратов: Изд-во СГУ, 1999. - 368 с.
5. Осовский С. Нейронные сети для обработки информации / Пер. с польского И.Д. Рудинского. - М.: Финансы и статистика, 2007. - 344 с.
6. Малинецкий Г.Г. Хаос. Структуры. Вычислительный эксперимент: Введение в нелинейную динамику. - М.: Эдиториал УРСС, 2006. - 256 с.
7. Капица С.П., Курдюмов С.П., Малинецкий Г.Г. Синергетика и прогнозы будущего. - М.: Эдиториал УРСС, 2001. - 288 с.
8. Хакен Г. Принципы работы головного мозга: Синергетический подход к активности мозга, поведению и когнитивной деятельности : пер. с англ. - М.: ПЕР СЭ, 2001. - 351 с. [Haken Н. Principles of Brain Functioning. A Synergetic Approach to Brain Activity, Behavior and Cognition.- Berlin: Springer, 1996.].
9. Stefanovska A., Luchinsky D. G., McClintock P. V. E. Modelling couplings among the oscillators of the cardiovascular system // Physiol. Meas. - 2001. - Vol. 22, no. 3. - P. 551-564.
Публикации с ключевыми словами: математическая модель, сердечно-сосудистая система, пульсовой механизм, нейронная сеть Вольтерра
Публикации со словами: математическая модель, сердечно-сосудистая система, пульсовой механизм, нейронная сеть Вольтерра
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



