научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#5 Май 2005
ИНТЕЛЛЕКТУАЛЬНЫЕ СИСТЕМЫ
В. И. Левин, д-р техн. наук, проф., Пензенский технологический институт
Интервальная математика и изучение неопределенных систем
Изложены основные положения базового раздела современной интервальной математики — интервальной алгебры. Показано ее сходство и отличие от алгебры вещественных чисел. Приведены простейшие примеры применения интервальной математики к изучению неопределенных систем.
Введение
На протяжении большей части своей истории человечество занималось интеллектуальной деятельностью, существенно используя понятие числа [1]. Это понятие совместно с хорошо известными действиями над числами — сложением, вычитанием, умножением, делением и сравнением — позволяли решать разнообразные задачи по изучению различных систем, возникающие в естественных, технических и гуманитарных науках. Однако задачи, решаемые современной наукой и современными технологиями, значительно усложнились, и одной из главных причин этого является неопределенность изучаемых систем. Поэтому для успешного решения новых сложных задач базовое математическое понятие числа, являющееся полностью определенным объектом, пришлось пересмотреть. В результате появилось понятие неопределенного числа. К настоящему времени известно три типа неопределенных чисел: случайные, нечеткие и интервальные. Случайные числа задаются некоторыми вероятностными распределениями их возможных значений; такие числа изучаются в теории вероятностей [2]. Нечеткие числа задаются лингвистически сформулированными распределениями их возможных значений; они изучаются в теории нечетких множеств [3]. Наконец, интервальные числа задаются интервалами их возможных значений без указания какого-либо распределения возможных значений числа внутри заданного интервала; они изучаются в интервальной математике [4]. Очевидно, что интервальные числа содержат минимальную информацию о неопределенном числе, которую проще всего получить. Отсюда — большой интерес, который представляют эти числа для различных приложений. Предлагаемая статья рассматривает некоторые основные вопросы теории интервальных чисел, образующие интервальную алгебру.
Интервальная алгебра дает средства для решения простейших задач изучения неопределенных систем. Кроме того, она лежит в основе других методов интервальной математики, позволяющих решать более сложные задачи изучения неопределенных систем.
1. Недетерминированные числа и недетерминированные функции
Пусть υ = f(x, у, ..., z) — обычная
вещественная функция от вещественных детерминированных аргументов. На практике,
когда информация об изучаемом объекте не полностью определена, аналогом функции
f становится соответствующая недетерминированная
функция F, вводимая следующим образом [5]. Пусть
аргументы х, у, ..., z функции f определены не полностью, а с
точностью до множеств возможных значений: ![]() . Тогда значение и функции f также окажется определенным не
полностью, а в виде соответствующего множества значений:
. Тогда значение и функции f также окажется определенным не
полностью, а в виде соответствующего множества значений: ![]() . При этом зависимость
множества V значений функции f от множеств X, Y, .., Z значений
ее аргументов и есть функция F, которая, таким
образом, может быть определена с помощью теоретико-множественной конструкции
. При этом зависимость
множества V значений функции f от множеств X, Y, .., Z значений
ее аргументов и есть функция F, которая, таким
образом, может быть определена с помощью теоретико-множественной конструкции
![]() (1)
(1)
Другими словами, значение V функции F при значениях ее аргументов X, Y, .., Z есть множество значений исходной функции f, когда ее аргументы х, у, ..., z пробегают множество значений соответственно X, Y,..., Z. Переход от f к F согласно (1) естественно назвать раздетерминизацией функции f. Положив в правой части (1) множество X, Y, ..., Z одноэлементным, превратим недетерминированную функцию F обычную f. Этот переход естественно назвать детерминизацией функции F. Функция F вида (1) преобразует множественные значения аргументов в множественное значение самой функции. В связи с этим функцию F можно назвать недетерминированной, а принимаемые ею самой и ее аргументами значения — недетерминированными числами.
Используя общее определение (1), можно ввести конкретные недетерминированные алгебраические функции:
сложение и вычитание
![]() (2)
(2)
умножение постоянной на переменную
![]() (3)
(3)
умножение переменных
![]() (4)
(4)
деление переменных
![]() (5)
(5)
возведение в степень
![]() (6)
(6)
и т. д. Многоместные недетерминированные функции сложения и умножения определяются аналогично двухместным функциям (2), (4).
Перейдем к логическим функциям. Пусть С = [А, В] — некоторый отрезок на вещественной оси. Его середина — точка М = (А + В)/2. Используя бинарные операции max, min, +, можно ввести на С следующие логические функции:
![]() (7)
(7)
![]()
Эти функции называются соответственно дизъюнкцией, конъюнкцией и отрицанием непрерывной логики (НЛ) [6]. Аналогично двухместным дизъюнкции и конъюнкции (7) вводятся их многоместные обобщения. Логические функции (7) раздетерминизируются подобно алгебраическим (6). При этом получаем недетерминированные логические функции
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
называемые соответственно недетерминированными дизъюнкцией, конъюнкцией и отрицанием НЛ.
Основной задачей в недетерминистской алгебре и логике является множественное вычисление функций, т. е. нахождение множественных значений V недетерминированных функций F вида (1) по заданным множественным значениям X, Y, ..., Z их аргументов. Заметим, что если раздетерминизируются числовые функции f, то получаются недетерминированные функции F с числовыми множествами значений аргументов X, Y, ..., Z и числовыми множествами значений функции V. Такие множества в общем случае имеют вид объединений непересекающихся вещественных интервалов.
2. Интервальные числа и интервальные функции
В частном случае, когда множества X, Y, ..., Z
в (1) — числовые, имеющие вид замкнутых интервалов, а функция f — непрерывная, множество V
также оказывается числовым в виде замкнутого интервала. Таким образом, в этом
конкретном случае недетерминированная функция F в (1) преобразует интервальные значения аргументов в
интервальное значение самой функции. В связи с этим функция F в данном случае может быть названа интервальной, а
принимаемые ею самой и ее аргументами значения — интервальными числами. Любое
интервальное число, таким образом, может быть записано в виде некоторого
замкнутого вещественного интервала ![]() . В итоге произвольная
интервальная функция может быть определена формально следующей
теоретико-множественной конструкцией — частным случаем конструкции (1):
. В итоге произвольная
интервальная функция может быть определена формально следующей
теоретико-множественной конструкцией — частным случаем конструкции (1):
![]() (11)
(11)
здесь и ниже
обозначено ![]() .
.
Используя общее определение (11), можно ввести конкретные интервальные алгебраические функции:
сложение и вычитание
![]() (12)
(12)
умножение постоянной на переменную
![]() (13)
(13)
умножение переменных
![]() (14)
(14)
деление переменных
![]() (15)
(15)
возведение в степень
![]() (16)
(16)
и т. д. Многоместные интервальные функции сложения и умножения определяются аналогично двухместным (12), (14). Подобно алгебраическим вводятся интервальные логические функции
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
называемые соответственно интервальными дизъюнкцией, конъюнкцией и отрицанием НЛ.
Основной задачей в интервальной алгебре и логике является вычисление
произвольной заданной интервальной функции, т. е. нахождение интервальных
значений ![]() интервальных
функций F вида (11) по заданным интервальным
значениям
интервальных
функций F вида (11) по заданным интервальным
значениям ![]() их
аргументов. Но произвольная интервальная функция может быть представлена в виде
суперпозиции некоторых элементарных интервальных функций вида (12)—(19).
Поэтому решение задачи вычисления произвольной интервальной функции всегда
может быть сведено к вычислению элементарных интервальных функций, выполняемому
по соответствующим простым правилам. Эти правила для элементарных
алгебраических функций таковы:
их
аргументов. Но произвольная интервальная функция может быть представлена в виде
суперпозиции некоторых элементарных интервальных функций вида (12)—(19).
Поэтому решение задачи вычисления произвольной интервальной функции всегда
может быть сведено к вычислению элементарных интервальных функций, выполняемому
по соответствующим простым правилам. Эти правила для элементарных
алгебраических функций таковы:
![]() (20)
(20)
![]() (21)
(21)
 (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
Обоснуем, например, правило (20). Складывая нижние (верхние) границы двух интервальных чисел, мы получаем наименьшее (наибольшее) значение их суммы. Известно, что вещественные числа обладают свойством полноты. В нашем случае это значит, что первое (второе) интервальное число может принять любое вещественное значение, лежащее между его границами. Но тогда сумма двух интервальных чисел может принять любое вещественное значение, лежащее между суммой нижних границ этих чисел и суммой их верхних границ. Последнее утверждение и есть правило (20). Аналогично обосновываются правила (21) - (24).
Правила, подобные правилам (20) — (24), можно получить и для вычисления элементарных логических функций:
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
Заметим, что правила (23), (24) для конкретных частных случаев упрощаются, принимая следующие формы:
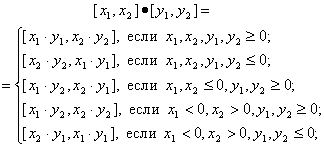 (28)
(28)
3. Алгебра интервальных чисел
Множество всех интервальных чисел совместно с определенными на нем элементарными операциями (функциями) (12) — (16) образует алгебру интервальных чисел. Эта алгебра частично похожа на всем известную алгебру вещественных чисел А, поскольку в ней выполняются следующие законы, аналогичные соответствующим в А:
![]() (коммутативность); (29)
(коммутативность); (29)
![]() (ассоциативность); (30)
(ассоциативность); (30)
![]() (
(![]() - единственный
нейтральный
- единственный
нейтральный
элемент сложения) (31)
![]() (
(![]() - единственный
нейтральный
- единственный
нейтральный
элемент умножения) (32)
![]() влечет
влечет ![]() или
или ![]() и обратно; (33)
и обратно; (33)
![]() (дистрибутивность
умножения на вещественное
(дистрибутивность
умножения на вещественное
число к относительно сложения интервальных чисел). (34)
Доказательства законов (29) — (34) просты и базируются непосредственно на определении входящих в них операций. Так, доказательство закона коммутативности сложения интервальных чисел (29) получается, если записать его левую часть согласно определению сложения (12), после чего на основании коммутативности сложения вещественных чисел поменять местами слагаемые x и y. В результате левая часть превратится в правую часть. Так же доказывается закон коммутативности умножения интервальных чисел (29). Для доказательства закона ассоциативности сложения интервальных чисел (30) запишем его левую часть по определению сложения (12) и преобразуем с учетом (12) и ассоциативности сложения вещественных чисел. Получим

что и
требовалось доказать. Так же доказывается закон ассоциативности умножения
интервальных чисел (30). Тождества (31), (32) с участием нейтрального элемента
сложения ![]() и
нейтрального элемента умножения
и
нейтрального элемента умножения ![]() следуют непосредственно из
определений сложения (12) и умножения (14) интервальных чисел. Причем если
предположить, например, существование двух элементов
следуют непосредственно из
определений сложения (12) и умножения (14) интервальных чисел. Причем если
предположить, например, существование двух элементов ![]() :
: ![]() и
и ![]() , то получим
, то получим ![]() , что
показывает
, что
показывает ![]() ,
т. е. единственность элемента
,
т. е. единственность элемента ![]() . Единственность элемента
. Единственность элемента ![]() доказывается
аналогично. Справедливость закона (33) следует из того, что:
доказывается
аналогично. Справедливость закона (33) следует из того, что:
1) если перемножаемые интервальные числа оба не равны ![]() , то их произведение,
согласно формуле (23), тоже не равно
, то их произведение,
согласно формуле (23), тоже не равно ![]() ;
;
2) если хотя бы одно интервальное число равно ![]() , то и произведение,
согласно (23), равно
, то и произведение,
согласно (23), равно ![]() .
.
Справедливость дистрибутивного закона (34) определяется следующим:

Заметим, что согласно (31), интервальное число ![]() (нуль-интервал) играет
в алгебре интервальных чисел ту же роль, что и число 0 в алгебре вещественных
чисел. Аналогично, согласно (32), интервальное число
(нуль-интервал) играет
в алгебре интервальных чисел ту же роль, что и число 0 в алгебре вещественных
чисел. Аналогично, согласно (32), интервальное число ![]() (единица-интервал)
имеет в алгебре интервальных чисел тот же смысл, что и число 1 в алгебре
вещественных чисел.
(единица-интервал)
имеет в алгебре интервальных чисел тот же смысл, что и число 1 в алгебре
вещественных чисел.
В алгебре интервальных чисел действительны также некоторые законы, отличающиеся от соответствующих в алгебре вещественных чисел, а именно:
♦ ![]() то
то ![]() и обратно, (35)
и обратно, (35)
т. е. в общем
случае разность равных интервальных чисел ![]() не равна нулю, а лишь включает
его. Эта разность равна нуль-интервалу
не равна нулю, а лишь включает
его. Эта разность равна нуль-интервалу ![]() , только если
, только если ![]() — вырожденное
интервальное число (интервал с совпадающим началом и концом);
— вырожденное
интервальное число (интервал с совпадающим началом и концом);
♦ ![]() то
то ![]() и обратно (36)
и обратно (36)
т. е. в общем
случае частное от деления равных интервальных чисел ![]() не равно единице, а
лишь включает ее. Это частное равно единице-интервалу
не равно единице, а
лишь включает ее. Это частное равно единице-интервалу ![]() , только если
, только если ![]() — вырожденное
интервальное число;
— вырожденное
интервальное число;
♦ если ![]() то
то ![]() и обратно (37)
и обратно (37)
т. е в общем случае невырожденное интервальное число (интервал с несовпадающими началом и концом) не имеет обратного интервального числа по сложению — его имеет только вырожденное интервальное число;
♦ если ![]() то
то ![]() и обратно, (38)
и обратно, (38)
т. е. в общем случае невырожденное интервальное число не имеет обратного интервального числа по умножению — его имеет только вырожденное интервальное число;
♦ ![]() (субдистрибутивность
общего случая умножения
(субдистрибутивность
общего случая умножения
на интервальное число относительно сложения таких чисел); (39)
♦ ![]() если
если ![]() для всех
для всех![]() (субдистрибутивность
частного
(субдистрибутивность
частного
случая умножения на интервальное число относительно сложения таких чисел). (40)
Доказательства законов (35) — (40) основаны на определении
соответствующих операций и правилах их выполнения. Так, доказательство закона (35)
следует из равенства ![]() , полученного по правилу (21).
, полученного по правилу (21).
Это равенство
показывает, что разность ![]() есть интервал, левая часть
которого не больше 0, а правая — не меньше 0, так что 0 — элемент этого интервала.
Также видим, что
есть интервал, левая часть
которого не больше 0, а правая — не меньше 0, так что 0 — элемент этого интервала.
Также видим, что ![]() только при x1
= x2 = x,
т. е при
только при x1
= x2 = x,
т. е при ![]() .
.
Аналогично доказательство закона (36) следует из равенства
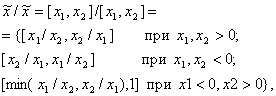
полученного
по правилам (23), (24). Это равенство показывает, что частное ![]() есть интервал,
левая часть которого не больше 1, а правая — не меньше 1, так что 1 — элемент
этого интервала.
есть интервал,
левая часть которого не больше 1, а правая — не меньше 1, так что 1 — элемент
этого интервала.
Кроме того,
видно, что ![]() =
1, только если реализуются первые два случая выписанного равенства, причем x1 = x2
= x, так что
=
1, только если реализуются первые два случая выписанного равенства, причем x1 = x2
= x, так что ![]() .
.
Доказательство закона (37) следует из того, что условие ![]() , согласно
правилу (20), дает x1 + y1 = x2
+ y2 = 0, откуда y1
= -x1, y2
= -x2. Но верхняя граница интервала
всегда не меньше нижней. Таким образом, имеем систему неравенств
, согласно
правилу (20), дает x1 + y1 = x2
+ y2 = 0, откуда y1
= -x1, y2
= -x2. Но верхняя граница интервала
всегда не меньше нижней. Таким образом, имеем систему неравенств ![]() единственное решение
которой x1 = x2
= x. Отсюда
единственное решение
которой x1 = x2
= x. Отсюда ![]() ,
, ![]() .
.
Доказательство закона (38) следует из того, что условие ![]() в соответствии
с правилом (23) означает следующее: а) все попарные произведения границ
интервалов
в соответствии
с правилом (23) означает следующее: а) все попарные произведения границ
интервалов ![]() и
и
![]() равны
между собой; б) эти произведения равны 1.
равны
между собой; б) эти произведения равны 1.
Записав утверждения а) и б) в виде ![]() . найдем x1
= x2 = x,
y1 = y2
= y, т. е.
. найдем x1
= x2 = x,
y1 = y2
= y, т. е. ![]() , y
= [1/x, 1/x].
, y
= [1/x, 1/x].
Доказательство закона (39) следует из цепочки равенств

в которой
знак включения ![]() , а не равенства (=), стоит
потому, что переменные x и x',
являясь независимыми переменными, могут принимать любые, в том числе неравные,
значения из множества
, а не равенства (=), стоит
потому, что переменные x и x',
являясь независимыми переменными, могут принимать любые, в том числе неравные,
значения из множества ![]() . Поэтому равенство в общем случае
не выполняется. Например, в случае
. Поэтому равенство в общем случае
не выполняется. Например, в случае ![]() имеем
имеем ![]() .
.
Доказательство закона (40) получим, считая в интервалах ![]() нижние границы
нижние границы
![]() (другой
возможный случай
(другой
возможный случай ![]() рассматривается аналогично). При
рассматривается аналогично). При ![]() с нижней
границей x1 ≥ 0 имеем по
правилам (20), (23):
с нижней
границей x1 ≥ 0 имеем по
правилам (20), (23):

т. е. в этом
случае утверждение (40) справедливо. При ![]() с верхней границей х2
≤ 0 рассмотрение сводим к предыдущему случаю заменой
с верхней границей х2
≤ 0 рассмотрение сводим к предыдущему случаю заменой ![]() на
на ![]() . Наконец, при x1 < 0, х2 > 0 имеем:
. Наконец, при x1 < 0, х2 > 0 имеем:
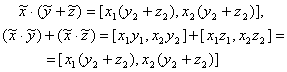
и опять утверждение (40) справедливо.
Наконец, в алгебре интервальных чисел действительны некоторые законы, которые вообще не имеют аналогов в алгебре вещественных чисел. Наиболее характерен из них закон монотонности включения:
![]() (41)
(41)
В формуле (41) F - любая одноместная интервальная функция, определяемая в виде
![]() (42)
(42)
с непрерывной функцией f, или двухместная интервальная функция “-“, “:” или n-местная при n ≥ 2 (в частности двухместная) интервальная функция “+”, “•”.
Доказательство закона (41) получается с помощью определения (11) интервальной функции. Например, для двухместной функции с использованием (11) получаем
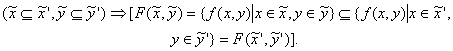
4. Некоторые особенности интервальных чисел и действий над ними
Согласно п. 2., всякое интервальное число ![]() характеризуется двумя параметрами
- нижней x1 и верхней x2 границами или, что эквивалентно, средним
значениям
характеризуется двумя параметрами
- нижней x1 и верхней x2 границами или, что эквивалентно, средним
значениям ![]() и
шириной
и
шириной ![]() .
Эта ситуация отлична от ситуации с вещественными числами, где каждое число
характеризуется одним параметром — значением этого числа. Далее, согласно п. 3,
законы действий над интервальными числами во многом отличаются от законов
действий над вещественными числами. Так, вычитание из интервального числа
равного ему в общем случае не приводит к нуль-интервалу [см. формулу (35)], как
и деление интервального числа на равное ему не дает единицы интервала [см.
формулу (36)]. Интервальные числа не имеют в общем случае обратных чисел ни по
сложению [формула (37)], ни по умножению [формула (38)]. Наконец, интервальные
числа в общем случае не обладают свойством дистрибутивности умножения
относительно сложения [формула (39)].
.
Эта ситуация отлична от ситуации с вещественными числами, где каждое число
характеризуется одним параметром — значением этого числа. Далее, согласно п. 3,
законы действий над интервальными числами во многом отличаются от законов
действий над вещественными числами. Так, вычитание из интервального числа
равного ему в общем случае не приводит к нуль-интервалу [см. формулу (35)], как
и деление интервального числа на равное ему не дает единицы интервала [см.
формулу (36)]. Интервальные числа не имеют в общем случае обратных чисел ни по
сложению [формула (37)], ни по умножению [формула (38)]. Наконец, интервальные
числа в общем случае не обладают свойством дистрибутивности умножения
относительно сложения [формула (39)].
Перечисленные особенности интервальных чисел приводят к значительной
специфике их использования на практике, где типичной задачей обычно является
оценка множества решений некоторой проблемы при интервально заданных
параметрах. Такова, например, задача оценивания диапазона wf
изменения вещественной функции f(x1,…, xn;
a1,…, am),
аргументы xi- и коэффициенты ai которой заданы интервалами ![]() и
и ![]() их возможных
значений, причем xi ai считаются независимыми. Оценочная функция в
этом случае берется в виде
их возможных
значений, причем xi ai считаются независимыми. Оценочная функция в
этом случае берется в виде ![]() , получаемом из исходной
вещественной функции заменой точечных операндов xi,
ai и операций над ними соответствующими
интервальными операндами
, получаемом из исходной
вещественной функции заменой точечных операндов xi,
ai и операций над ними соответствующими
интервальными операндами ![]() и операциями. На основании закона
(41) имеем соотношение
и операциями. На основании закона
(41) имеем соотношение
![]() (43)
(43)
которое служит средством получения искомой оценки. Для этого вычисляется интервальная функция F от интервальных параметров в правой части (43) с использованием правил, описанных в п. 2. Полученное в результате интервальное число — значение функции F и будет, согласно (43), оценкой сверху диапазона wf изменения вещественной функции f.
В процессе вычисления интервальной оценочной функции F ширина интервала-величины F может в некоторых случаях достигать больших значений, многократно превышающих ширину величин ее аргументов. Этот эффект можно трактовать как возрастание неопределенности оценки вещественной функции по отношению к неопределенностям оценок ее аргументов. Такое возрастание может приводить к тому, что интервальные оценки некоторых вещественных функций становятся практически бесполезными.
Другой эффект, связанный с получением интервальных оценок диапазона изменения вещественной функции f, заключается в зависимости ширины получаемой оценки от выбранного аналитического выражения для f. Это обстоятельство побуждает выбирать для f лишь те аналитические выражения, которые ведут к минимальной ширине оценки. Оба указанных эффекта отсутствуют при работе с вещественными (неинтервальными) функциями, где аналогом рассмотренной задачи является обычное вычисление функции.
Пример 1. Оценим полную поверхность S
прямоугольного параллелепипеда со сторонами a, b, c, заданными неточно: ![]() . Полная
поверхность прямоугольного параллелепипеда, как известно, определяется по
формуле
. Полная
поверхность прямоугольного параллелепипеда, как известно, определяется по
формуле
S = 2(ab + bc + сa).
Заменив в этой формуле точные значения a, b, c заданными приближенными, представленными в
интервальной форме , получим, согласно (43), следующую оценку диапазона ws изменения величины S:
![]()
После вычисления интервальных произведений и сумм согласно (20), (22), (28) получим нужную оценку:
![]() или
1080≤S≤1540.
или
1080≤S≤1540.
Оценки для S можно найти и на основе других формул определения S, полученных из приведенной формулы путем эквивалентных преобразований (вынесения за скобки a, b или c). Эти оценки либо совпадают с полученной, либо хуже нее (границы для S шире).
Пример 2. Оценим площадь S прямоугольника, сумма соседних сторон которого равна 1, а сама сторона может принять любое значение от 0 до 1. Обозначим одну из соседних сторон а. Тогда другая сторона равна 1 - a. Площадь прямоугольника определится по формуле
S = a(l - a).
Заменив в ней точное значение а заданным приближенным, представленным в интервальной
форме ![]() = [0, 1],
получим согласно (43) оценку диапазона wS
изменения S:
= [0, 1],
получим согласно (43) оценку диапазона wS
изменения S:
![]()
После интервальных вычислений согласно (21), (28) получим:
![]() или 0 ≤
S ≤ 1.
или 0 ≤
S ≤ 1.
Беря для определения S другие формулы, получаемые из приведенной формулы путем эквивалентных преобразований, найдем другие оценки:
·
при ![]() или -1 ≤ S ≤ 1, откуда, учитывая, что всегда S ≥ 0, имеем 0 ≤ S ≤ 1;
или -1 ≤ S ≤ 1, откуда, учитывая, что всегда S ≥ 0, имеем 0 ≤ S ≤ 1;
·
при ![]() или
0 ≤ S ≤ ½;
или
0 ≤ S ≤ ½;
·
при ![]() или 0 ≤ S ≤ ¼.
или 0 ≤ S ≤ ¼.
Хорошо видно, что качество оценки сильно зависит от вида формулы для определения S. Лучшая (самая узкая) из полученных оценок подчеркнута. Легко убедиться (например, решив задачу max a(1 - a) при 0 ≤ a ≤ 1), что эта оценка уже не улучшаема.
* * *
В статье представлены лишь начальные сведения по алгебре интервальных чисел, связанные с простейшими задачами изучения систем в условиях интервальной неопределенности, сводящимися к вычислению функций с интервальными аргументами и коэффициентами.
Примерами подобных задач могут служить: получение оценок характеристик систем, параметры которых известны с точностью до интервала; автоматический контроль погрешности округлений при вычислениях на компьютере; планирование и автоматизация научных экспериментов и ряд других. Более сложные применения интервальных чисел, связанные с задачами оптимизации, управления, контроля, принятия решений и т. д. упираются в необходимость сравнения указанных чисел. Эти вопросы будут рассмотрены отдельно.
Список литературы
1. Фрид Э., Пастор И., Рейман И. и др. Малая математическая энциклопедия. Будапешт: Изд-во АН Венгрия, 1976. 695 с.
2. Феллер В. Введение в теорию вероятностей и ее приложения. М.: Мир. Т. 1. 1964. 500 с; Т. 2. 1967. 752 с.
3. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. М.: Мир, 1976. 168 с.
4. Алефельд Г. Херцбергер Ю. Введение в интервальные вычисления. М.: Мир, 1987. 360 с.
5. Левин В. И. Расчет динамических процессов в дискретных автоматах с неопределенными параметрами с помощью недетерминистской бесконечнозначной логики // Кибернетика и системный анализ, 1992. № 3. С. 15—30.
6. Левин В. И. Непрерывная логика и ее применение // Информационные технологии. 1997. № 1. С. 17—21.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 6, 1998
ИНТЕЛЛЕКТУАЛЬНЫЕ СИСТЕМЫ
Ключевые слова: Интервальная математика, недетерминированные функции, алгебра интервальных чисел, неопределённые системы.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



