научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#5 Май 2005
А. К. Азов, канд. техн. наук, А. А. Ожиганов, д-р техн. наук, М. В. Тарасюк, Санкт-Петербургский государственный институт точной механики и оптики (технический университет)
Рекурсивные кодовые шкалы
Рассмотрены теоретические аспекты построения однодорожечных кодовых шкал для преобразователей угловых перемещений. Даны анализ предлагаемых шкал, а также их классификация по типу используемой рекурсивной последовательности. Приведены примеры рекурсивных шкал.
Введение
Внедрение управляющих систем с использованием ЭВМ в различные отрасли промышленности обеспечивает решение разнообразных задач управления технологическими процессами и обработки информации, представляемой в цифровой форме.
Высокие показатели современных ЭВМ по быстродействию, точности, объему памяти запоминающих устройств и возможности организовать работу управляющего комплекса по любому желаемому алгоритму — вот те основные технические факторы, которые неуклонно стимулируют дальнейшее развитие систем управления на основе управляющих ЭВМ.
При проектировании систем управления приходится решать задачу связи ЭВМ с управляемым объектом, поскольку информация, поступающая от объекта, и информация, используемая в ЭВМ, представляются в различных формах.
Учитывая, что информация от объекта имеет в основном непрерывный характер, а информация, с которой оперирует цифровая ЭВМ, всегда дискретного характера, эта задача сводится к выполнению аналого-цифрового и цифроаналогового преобразования.
Распространенными устройствами для выполнения аналого-цифрового преобразования являются преобразователи углового перемещения в код. В настоящее время существует большое число различных типов преобразователей перемещения, наиболее перспективными из которых считаются преобразователи, построенные по методу параллельного считывания (абсолютного отсчета). Основной элемент таких преобразователей — кодовая шкала (КШ). Она имеет число информационных кодовых дорожек (КД), как правило, равное разрядности устройства и поэтому, в основном, определяет сложность изготовления всего преобразователя [1].
В работе [2] был предложен метод построения кодовых шкал на основе двоичных линейных рекурсивных последовательностей, более технологичных в изготовлении по сравнению с классическим КШ. Такие шкалы содержат одну информационную дорожку, маска (кодовый рисунок) которой выполняется в соответствии с псевдослучайным законом. Варианты построения рекурсивных кодовых шкал (РКШ) — псевдослучайных (ПСКШ) и композиционных (ККШ) — рассмотрены в работах [2, 3].
Теоретические аспекты построения рекурсивных кодовых шкал
Псевдослучайные КШ содержат одну информационную КД, выполненную в соответствии с символами псевдослучайной двоичной последовательности максимальной длины (М-последовательности) {aj}, j = 0, 1,…, L - 1, и n считывающих элементов. Элементы размещаются вдоль дорожки с возможностью получения с них при полном перемещении шкалы L = 2n - 1 различных n-разрядных кодовых комбинаций, что обеспечивает получение разрешающей способности шкалы δ = 360o/L.
Для построения М-последовательности длины L используется примитивный неприводимый полином h(x) степени n с коэффициентом из поля Галуа (GF(2)), т. е.
![]() (1)
(1)
где h0 = hn = 1, а hi = {0, 1} при 0 < i < n.
Символы an+j М-последовательности удовлетворяют рекурсивному соотношению
![]() (2)
(2)
где знак ![]() означает
суммирование по модулю два. Начальные значения символов последовательности a0 a1
… an - 1 выбираются произвольно, за
исключением нулевой комбинации.
означает
суммирование по модулю два. Начальные значения символов последовательности a0 a1
… an - 1 выбираются произвольно, за
исключением нулевой комбинации.
Дальнейшим развитием псевдослучайных кодовых шкал явились композиционные кодовые шкалы. Они, так же как и псевдослучайные шкалы, имеют одну информационную КД, но выполненную уже в соответствии с символами двоичной последовательности {Aj},j = 0, 1, 2, ..., R - 1, названной композиционной (Кр - последовательность). Считывающие элементы, число которых равно N, размещаются вдоль дорожки с возможностью получения при полном перемещении шкалы R различных N-разрядных кодовых комбинаций, что обеспечивает получение разрешающей способности шкалы δ = 360o/R.
Для получения Кр - последовательности используется полином H(x) степени N с коэффициентами GF(2), т. е.
![]() (3)
(3)
где hk(x) определяется в соответствии с (1); p = 1, 2,...,
![]() (4)
(4)
Символы AN + j Кр - последовательности удовлетворяют рекурсивному соотношению
![]() (5)
(5)
Начальные значения символов Кр - последовательности A0, A1,..., AN - 1 выбираются так, что наибольший общий делитель (НОД)
[Tj(x), H(x)] = 1,
где
![]() (6)
(6)
Для практических применений достаточно взять Tj(x) = 1, т. е. A0 = A1 = ... = AN - 2 = 0, AN - 1 = 1.
Период R Кр - последовательности зависит от степени полиномов hk(x) и полинома начальных значений символов Кр - последовательности Tj(x). Если все nk представляют собой взаимно простые числа, а НОД [Tj(x), H(x)] = 1, то
![]() (7)
(7)
где ![]() .
.
Отметим, что при p = 1 композиционная последовательность (3) превращается в классическую М-последовательность.
Наряду с рекурсивными КШ, построенными с использованием линейных последовательностей, известны кодовые шкалы, построенные на основе нелинейных рекурсивных последовательностей — нелинейные рекурсивные кодовые шкалы (НКШ) [4, 5].
Кодовая дорожка НКШ выполняется в соответствии с символами нелинейной рекурсивной последовательности (НП) {bj},j = 0, 1, ..., B - 1. Считывающие элементы, число которых равно n, размещаются вдоль дорожки с возможностью получения при полном перемещении шкалы В = 2n различных n-разрядных кодовых комбинаций, что обеспечивает получение разрешающей способности шкалы δ = 360o/B.
Символы bn + j НП удовлетворяют рекурсивному соотношению
![]() (8)
(8)
где hi — коэффициенты, зависящие от вида примитивного неприводимого полинома (1),
 (9)
(9)
а индексы при символах последовательности берутся по модулю В. Начальные значения символов b0 b1 … bn - 1 последовательности выбираются произвольно.
Первое слагаемое в (8) определяет правило получения М-последовательностей согласно (2), а второе — указывает на операцию умножения значений n — 1 кодовых символов.
При построении РКШ символы М-последовательности a0 a1 … aL - 1, Кр - последовательности А0 А1 ... AR - 1 и НП b0 b1 ... bB - 1 отображаются на информационной КД шкалы, причем символам 1 последовательностей соответствуют активные, а символам 0 пассивные элементарные участки информационной дорожки, равные δ. Для обеспечения разрешающей способности δ необходимо решить задачу размещения считывающих элементов (СЭ), так как не любой вариант расположения СЭ позволяет получить при полном обороте шкалы все различные кодовые комбинации.
Линейные рекурсивные последовательности (ЛРП) — псевдослучайные и Кр - последовательности — могут задаваться порождающим полиномом вида
G(x) = (xR + 1)/H(x), (10)
где R = L, N = n и H(x) = h(x) при p = 1.
Для каждой ЛРП длиной R существует ровно R различных циклических сдвигов, которые могут быть получены путем умножения порождающего полинома G(x) на xI, где I = 0, 1, ..., R - 1.
Поскольку РКШ на основе псевдослучайных и композиционных
последовательностей строятся в соответствии с символами ЛРП, то можно путем
циклических сдвигов задать порядок размещения на шкале N считывающих
элементов, т. е. m-му СЭ, m
= 1, 2, ..., N, ставится в соответствие Im-й циклический сдвиг ![]() последовательности.
Тогда полином, определяющий порядок размещения N СЭ на шкале, имеет вид
последовательности.
Тогда полином, определяющий порядок размещения N СЭ на шкале, имеет вид
 (11)
(11)
где ![]() . Положив I1 = 0, из (11) однозначно определяется
положение второго, третьего,..., N-го СЭ,
смещаемых относительно первого СЭ на I2,
I3,…, IN
элементарных участков δ информационной дорожки шкалы
соответственно.
. Положив I1 = 0, из (11) однозначно определяется
положение второго, третьего,..., N-го СЭ,
смещаемых относительно первого СЭ на I2,
I3,…, IN
элементарных участков δ информационной дорожки шкалы
соответственно.
Так как псевдослучайные и композиционные последовательности линейны по отношению к оператору суммирования по модулю два, алгоритм размещения N СЭ на РКШ сводится к нахождению подходящего линейно независимого множества из N циклических сдвигов ЛРП [б, 7, 8].
Рекурсивные КШ на основе нелинейных последовательностей требуют размещения на шкале n СЭ в соответствии с полиномом размещения
![]() (12)
(12)
Исследования показали, что рекурсивные кодовые шкалы на основе линейных последовательностей обладают хорошими корректирующими свойствами (позволяют формировать с единственной информационной дорожкой коды с необходимым минимальным кодовым расстоянием); нелинейные кодовые шкалы такими возможностями не обладают. Еще одним недостатком НКШ является необходимость размещения СЭ с шагом, соответствующим размеру элементарного участка шкалы δ.
Проведем анализ рекурсивных кодовых шкал, положив в основу следующие признаки:
· число наносимых границ смены рисунка кодовой маски шкалы;
· число кодовых дорожек;
· число считывающих элементов;
· разрешающая способность;
· однопеременность кода, используемого для получения кодовой маски шкалы;
· регулярность структуры рисунка кодовой маски шкалы;
· возможность формирования корректирующих кодов без использования дополнительных кодовых дорожек;
· необходимость преобразования кода, получаемого со шкалы, в обыкновенный двоичный (ОДК).
Как отмечалось выше, ПСКШ строятся на основе М-последовательностей с периодом L. В периоде L из общего числа 2n - 1 серий следующих друг за другом одинаковых символов серии из одного символа (0 или 1) встречаются 2n – 2 раз, из двух символов (00 или 11) — 2n - 3 раз, из трех символов (000 или 111) — 2n - 4 раз и т. д., серии из n - 1 нулей и n единиц встречаются по одному разу.
Очевидно, что число границ смены кода (7) для ПСКШ равно числу серий следующих друг за другом одинаковых символов, т. е.
TПС = 2n - 2(13)
где n — разрядность шкалы и число СЭ. ПСКШ содержат всего одну информационную кодовую дорожку и имеют разрешающую способность
δПС= 360o/(2n - 1).
Опуская математические выкладки, учитывающие свойства М- и Кр - последовательностей, приведем конечную формулу для расчета числа границ смены кода ККШ, которая имеет вид
 (14)
(14)
где ![]() ; p — порядок Кр - последовательности; R
определяется в соответствии с (7). Композиционные КШ, так же как и ПСКШ, имеют
всего одну КД с числом N считывающих элементов, которое рассчитывается из (4).
Разрешающая способность ККШ δККШ = 360°/R.
; p — порядок Кр - последовательности; R
определяется в соответствии с (7). Композиционные КШ, так же как и ПСКШ, имеют
всего одну КД с числом N считывающих элементов, которое рассчитывается из (4).
Разрешающая способность ККШ δККШ = 360°/R.
Псевдослучайные и композиционные КШ позволяют формировать корректирующие коды только за счет введения избыточности по числу СЭ без использования дополнительных КД; кодовые шкалы на основе нелинейных последовательностей такими корректирующими возможностями не обладают.
Для НКШ число наносимых границ смены кода и число считывающих элементов равны соответствующим параметрам ПСКШ, а разрешающая способность равна разрешающей способности классических КШ, выполненных в ОДК или в коде Грея.
Кодовые маски всех РКШ имеют нерегулярный рисунок КД и однопеременностью не обладают. Для преобразования рекурсивного кода в ОДК необходима пересчетная или комбинационная схема.
Классификация рекурсивных кодовых шкал
Рассмотрим классификацию РКШ (рис. 1) по типу используемой для получения маски кодовой дорожки шкалы рекурсивной последовательности (РП).
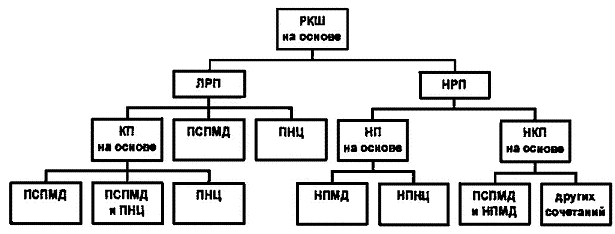
Рис. 1
В качестве первого классификационного признака используется свойство линейности РП по отношению к оператору суммирования по модулю два. По этому признаку РКШ делятся на две группы: КШ на основе линейных РП (ЛРП) и КШ на основе нелинейных РП (НРП).
В свою очередь, КШ на основе линейных РП подразделяются на три группы: КШ на основе псевдослучайных последовательностей максимальной длины (ПСПМД), КШ с использованием последовательностей неполных циклов (ПНЦ) и КШ на основе композиционных последовательностей (КП).
Принципы построения КШ на основе ПСПМД (М-последовательностей) рассмотрены в работе [2]. При получении рекурсивного соотношения, используемого для генерации символов М-последовательности, берутся только примитивные полиномы. Кодовые шкалы на основе ПСПМД получили название ПСКШ.
Кодовые шкалы на основе ПНЦ строятся аналогично ПСКШ. Последовательности
неполных циклов синтезируются с использованием неприводимых (над GF(2)) полиномов. Примером такого полинома может быть
полином четвертой степени h(x)
= x4 + x3
+ x2 + x+
1, а соответствующее ему рекурсивное соотношение имеет вид ![]() . При ненулевых начальных
условиях это соотношение позволяет генерировать линейную рекурсивную
последовательность длиной пять (00011). Если эту РП использовать для получения
кодовой маски шкалы, то при размещении вдоль нее четырех СЭ, например, с шагом,
равным одному элементарному участку, можно получить пять различных
четырехразрядных кодовых комбинаций. Однако такие КШ будут иметь меньшую, по
сравнению с ПСКШ, разрешающую способность.
. При ненулевых начальных
условиях это соотношение позволяет генерировать линейную рекурсивную
последовательность длиной пять (00011). Если эту РП использовать для получения
кодовой маски шкалы, то при размещении вдоль нее четырех СЭ, например, с шагом,
равным одному элементарному участку, можно получить пять различных
четырехразрядных кодовых комбинаций. Однако такие КШ будут иметь меньшую, по
сравнению с ПСКШ, разрешающую способность.
Кодовые шкалы на основе композиционных последовательностей могут быть разделены на три группы: КШ на основе композиционных последовательностей, когда КП получаются из различных сочетаний М-последовательностей; КШ на основе композиционных последовательностей, где КП получаются из сочетаний М-последовательностей и ПНЦ; КШ на основе композиционных последовательностей, где КП получаются из различных сочетаний ПНЦ.
Принципы построения КШ на основе КП, получаемых из различных сочетаний М-последовательностей, рассмотрены в работе [3]. Именно такие шкалы названы ККШ. Шкалы второй и третьей групп строятся аналогично ККШ. Наименьшей разрешающей способностью обладают КШ на основе РП третьей группы, наибольшей — ККШ, а КШ второй группы занимают по этому параметру промежуточное положение.
Кодовые шкалы на основе нелинейных РП подразделяются на две группы: КШ на основе нелинейных последовательностей (НП) и КШ с использованием нелинейных КП (НКП).
В свою очередь, шкалы, в основу которых положены НП, также делятся на две группы: КШ с использованием НП максимальной длины (НПМД) и КШ на основе НП неполных циклов (НПНЦ).
Принципы построения КШ с использованием НПМД рассмотрены в работе [5]. При получении рекурсивного соотношения, определяющего порядок получения символов НПМД, берутся примитивные полиномы с введением в рекурсивное соотношение дополнительного слагаемого. Такие шкалы получили название НКШ.
Шкалы на основе НПНЦ строятся аналогично НКШ. Получение НПНЦ подробно рассмотрено в работе [9]. Последовательности неполных циклов также позволяют строить КШ, однако их разрешающая способность будет заведомо меньше, чем разрешающая способность КШ на основе НПМД.
Кодовые шкалы на основе НКП могут быть разделены на две группы: КШ на основе НКП, где НКП получаются из сочетаний М-последовательностей и НПМД, и КШ на основе НКП, когда НКП получаются из различных сочетаний линейных и нелинейных последовательностей как максимальных, так и неполных циклов.
Принципы построения КШ на основе НКП аналогичны принципам построения любых рассмотренных выше рекурсивных шкал. Наилучшей разрешающей способностью будут обладать КШ, где НКП получаются из сочетаний М-последовательностей и НПМД, а шкалы, когда НКП получаются из других сочетаний линейных и нелинейных последовательностей, обладают, по сравнению с первыми, меньшей разрешающей способностью.
Примеры рекурсивных кодовых шкал
На рис. 2 приведена линейная развертка круговой четырехразрядной ПСКШ с установкой четырех СЭ.

Рис.2
Информационная КД выполнена в соответствии с символами
М-последовательности {aj} = a0 a1…a14 = 000100110101111 длиной L = 15, для построения которой использован примитивный
неприводимый полином h{x}
= х4 + x + 1, а символы a4 + j
последовательности при начальных значениях а0 = а1
= а2 = 0, а3 = 1 удовлетворяют рекурсивному
соотношению ![]() .
.
Порядок размещения четырех информационных СЭ вдоль дорожки ПСКШ определяется полиномом r(x) = 1 + х3 + х6 + х9, где второй, третий и четвертый СЭ смещены относительно первого СЭ (I1 = 0) (на рис. 2 слева направо) на I2 = 3, I3 = 6, I4 = 9 элементарных участков δ = 360°/15 КД шкалы соответственно.
При перемещении ПСКШ на выходах считывающих элементов последовательно формируются кодовые комбинации сигналов 0111, 0010, 0001, 1111, 0101, 0011, 1110, 1010, 0110, 1101, 0100, 1100, 1011, 1001, 1000, соответствующие пятнадцати угловым положениям.
На рис. 3 приведена линейная развертка круговой пятиразрядной ККШ с установкой пяти СЭ.

Рис. 3
Информационная дорожка шкалы выполнена в соответствии с символами K2-последовательности {Аj} = A0 A1 ... А20 =
000011111010100110001 длиной R = 21, для построения
которой использован полином H(x) = h1(x) h2(x) = (х2 + х + l)(x3 + х + 1) = х5 + х4
+ 1 (по mod 2), а символы А5 + j- K2-последовательности
при начальных значениях A0 = А1
= А2 = А3 = 0, А4 = 1
удовлетворяют рекурсивному соотношению ![]() . Порядок размещения пяти СЭ вдоль
дорожки ККШ определяется полиномом r(х) =
1 + х4 + х8 + х12 + х16.
. Порядок размещения пяти СЭ вдоль
дорожки ККШ определяется полиномом r(х) =
1 + х4 + х8 + х12 + х16.
При перемещении ККШ на выходах считывающих элементов последовательно формируются сигналы, образующие кодовые комбинации 01111, 01000, 01100, 01010, 11111, 10000, 11000, 10100, 11110, 00001, 10001, 01001, 11101, 00011, 00010, 10011, 11010, 00111, 00100, 00110, 10101, которые соответствуют двадцати одному угловому положению шкалы.
На рис. 4 приведена линейная развертка круговой четырехразрядной НКШ с установкой четырех СЭ.

Рис. 4
Информационная дорожка шкалы выполнена в соответствии с символами
нелинейной последовательности {bj} = b0 b1
... bl5 =
0000100110101111 длиной В = 2n
= 24 = 16, для построения которой использован примитивный неприводимый полином h(x) = х4
+ х + 1, а символы b4 + j последовательности {bj}
при начальных значениях b0 = b1 = b2
= b3 = 0 удовлетворяют рекурсивному
соотношению ![]() .
В примере размещение четырех СЭ вдоль кодовой дорожки определяется полиномом r(х) = 1 + х + х2 + х3.
.
В примере размещение четырех СЭ вдоль кодовой дорожки определяется полиномом r(х) = 1 + х + х2 + х3.
При перемещении шкалы на выходах СЭ могут быть зафиксированы шестнадцать четырехразрядных кодовых комбинаций 0000, 0001, 0010, 0100, 1001, 0011, 0110, 1101, 1010, 0101, 1011, 0111, 1111, 1110, 1100, 1000.
Список литературы
1. Домрачев В. Г. Мейко Б. С. Цифровые преобразователи угла: принципы построения, теория точности, методы контроля. М.: Энергоатомиздат, 1984. 328 с.
2. Ожиганов А. А. Псевдослучайные кодовые шкалы // Приборостроение, 1987. Т. 30. № 2. С. 40—43.
3. Ожиганов А. А., Тарасюк М. В. Композиционные кодовые шкалы // Приборостроение, 1994. Т. 37. № 5—6. С. 26—29.
4. Petriu E. Absolute-type pseudorandom shaft encoder with any desired resolution // "El. lette", 1985. № 5. P. 215—216.
5. Ожиганов А. А. Метод построения кодовых шкал на основе нелинейных двоичных последовательностей // Деп. в ВИНИТИ, 1995. № 1541-В95, 4 с.
6. Ожиганов А. А. Алгоритм размещения считывающих элементов на псевдослучайной кодовой шкале // Приборостроение, 1994. Т. 37. С. 22—27.
7. Ожиганов А. А., Тарасюк М. В. Размещение с постоянным шагом считывающих элементов на псевдослучайной кодовой шкале // Приборостроение, 1994. Т. 37. № 11—12. С. 23-26.
8. Ожиганов А. А., Тарасюк М. В. Размещение считывающих элементов на композиционной кодовой шкале // Приборостроение, 1997. Т. 40. № 1. С. 42—47.
9. Агульник А. Р., Мусаелян С. С. Построение нелинейных двоичных последовательностей // Радиоэлектроника. 1983. № 4. С. 19-28.
ПРИКЛАДНЫЕ ИНФОРМАЦИОННЫЕ СИСТЕМЫ
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 6, 1998
Ключевые слова: Аналого-цифровые преобразования, кодовая шкала, рекурсивные последовательности, классификация кодовых шкал.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



