научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2013
DOI: 10.7463/0113.0508634
УДК 629.7.018.7
Россия, МГТУ им. Н.Э. Баумана
ГНМЦ МО РФ
marmotto@rambler.ru
mp.gnmc@mail.ru
Введение
Высокая точность бортовых измерений параметров полета, правильная оценка возникающих при этом погрешностей играют существенную роль в летных испытаниях, в обеспечении безопасности полетов, на других этапах жизненного цикла летательного аппарата. Существующие средства бортовых измерений и регистрации в основном удовлетворяют заданным требованиям, что подтверждается наземными и летными испытаниями, а также практикой эксплуатации воздушных судов. С другой стороны, погрешности бортовых средств измерений, содержащиеся в перечне их технических характеристик, оцениваются автономно и во многих случаях только для установившихся значений входных сигналов, то есть без учета динамических погрешностей [1].
Между тем, точность измерений таких важнейших параметров полета, как углы атаки и скольжения, перегрузки, высота и скорость полета (статическое и динамическое давление) существенно зависит от координат установки датчиков, положения центра масс самолета, длины трубопроводов давления и других технических особенностей бортовых систем, а также от режима полета и вида маневра. Современные цифровые системы регистрации, в свою очередь, вносят дополнительные погрешности, среди которых наиболее значительными обычно являются сдвиги по времени, возникающие вследствие неточной синхронизации разнородных информационных потоков, а также из-за отсутствия учета последовательности опроса датчиков в пределах информационного кадра. В последние годы разработан ряд методов комплексного оценивания погрешностей бортовых измерений, прежде всего, на основе использования спутниковых навигационных систем [2-5].
Рассматриваемые погрешности являются динамическими и связаны с движением самолета. Их учет приобретает особую актуальность, например, в задачах послеполетного контроля пилотирования вблизи эксплуатационных ограничений, при расследовании летных происшествий. Выявление и коррекция указанных погрешностей имеет существенное значение также при использовании современных алгоритмов цифровой обработки полетных данных, например, в целях идентификации аэродинамических коэффициентов летательных аппаратов [6-11].
Предлагаемый алгоритм является развитием методов контроля правильности бортовых измерений, основанных на использовании известных из динамики полета уравнений движения летательных аппаратов [6-8], от которых он отличается выбором идентифицируемых параметров системы измерений. Это позволяет эффективно выявлять динамические погрешности бортовых измерений. Кроме того, предлагаемый алгоритм реализован в виде программы для ЭВМ с развитым графическим интерфейсом, что позволяет рекомендовать его для использования инженерным составом, не владеющим методами теории идентификации систем, и тем самым определяет его практическую значимость. Представленные в статье результаты апробации алгоритма по данным летных испытаний наглядно раскрывают возможности предлагаемого подхода и основные методические приемы выявления с его помощью погрешностей бортовых измерений.
1 Алгоритм контроля правильности бортовых измерений параметров полета
Поскольку погрешности носят ярко выраженный системный характер, для их оценивания целесообразно применить системный подход. В настоящей работе для этой цели используются соотношения между параметрами полета, определяемые уравнениями пространственного движения самолета.
Из общей модели пространственного движения самолета [12] выделяются следующие уравнения:
 ,
,
 ,
,
 , (1)
, (1)
 ,
,
 .
.
Здесь ![]() – углы атаки и скольжения, рад;
– углы атаки и скольжения, рад;
![]() – угловые скорости относительно связанных осей, рад/с;
– угловые скорости относительно связанных осей, рад/с;
![]() – углы тангажа, крена, рыскания, рад;
– углы тангажа, крена, рыскания, рад;
![]() – истинная воздушная скорость, м/с;
– истинная воздушная скорость, м/с;
![]() - ускорения вдоль связанных осей, определяемые формулами
- ускорения вдоль связанных осей, определяемые формулами
![]() ,
,
![]() , (2)
, (2)
![]() ,
,
где ![]() - перегрузки вдоль связанных осей.
- перегрузки вдоль связанных осей.
Главная особенность этих уравнений заключается в том, что они не зависят от аэродинамических коэффициентов самолета, поскольку входящие в правые части ускорения можно вычислить через измеряемые в полете значения перегрузок.
Уравнения (1), (2) в векторной форме имеют вид
![]() , (3)
, (3)
где ![]() - векторы выходных и входных сигналов,
- векторы выходных и входных сигналов,
![]() - вектор параметров.
- вектор параметров.
В данном случае вектор ![]() состоит из сигналов
состоит из сигналов ![]()
![]() . В вектор входных сигналов входят измеренные в полете значения угловых скоростей
. В вектор входных сигналов входят измеренные в полете значения угловых скоростей ![]() и перегрузок
и перегрузок ![]() .
.
Начальные условия ![]() задаются по результатам измерений параметров
задаются по результатам измерений параметров ![]()
![]() в момент начала участка обработки.
в момент начала участка обработки.
Непосредственное численное интегрирование системы дифференциальных уравнений (1) с учетом (2) в общем случае не дает положительных результатов, поскольку постоянные составляющие погрешностей измерений входных сигналов ![]() и
и ![]() приводят к появлению погрешности типа линейного тренда, что не позволяет сравнивать выходные сигналы модели и объекта. Для устранения этого эффекта введем вектор неизвестных параметров
приводят к появлению погрешности типа линейного тренда, что не позволяет сравнивать выходные сигналы модели и объекта. Для устранения этого эффекта введем вектор неизвестных параметров ![]() , состоящий из постоянных составляющих погрешностей измерений сигналов
, состоящий из постоянных составляющих погрешностей измерений сигналов ![]() и
и ![]() :
:
![]() . (4)
. (4)
Для нахождения оценок параметров (4) применим, например, алгоритм идентификации по максимуму правдоподобия. Модель наблюдений в векторной форме имеет вид
![]() , (5)
, (5)
где ![]() - шум наблюдений, представляющий собой векторную нормальную случайную последовательность типа белого шума с нулевым математическим ожиданием и постоянной дисперсионной матрицей
- шум наблюдений, представляющий собой векторную нормальную случайную последовательность типа белого шума с нулевым математическим ожиданием и постоянной дисперсионной матрицей ![]() . В вектор наблюдений включаются сигналы, производные которых стоят в левой части (1):
. В вектор наблюдений включаются сигналы, производные которых стоят в левой части (1):
![]() . (6)
. (6)
Минимизируемый функционал принимает вид
 , (7)
, (7)
где ![]() - выходной сигнал модели объекта;
- выходной сигнал модели объекта; ![]() - число измерений на участке обработки. Алгоритм численной оптимизации, используемый для нахождения оценок параметров, является модификацией классического метода Ньютона [13]. Детальное описание используемого алгоритма идентификации дано в [14].
- число измерений на участке обработки. Алгоритм численной оптимизации, используемый для нахождения оценок параметров, является модификацией классического метода Ньютона [13]. Детальное описание используемого алгоритма идентификации дано в [14].
Рассмотренный алгоритм обеспечивает нахождение постоянных погрешностей измерений угловых скоростей и перегрузок.
В случае правильно функционирующей бортовой системы измерений и регистрации степень соответствия измеренных в полете и вычисленных в модели сигналов является весьма высокой даже на режимах интенсивного маневрирования.
Рассматриваемый подход позволяет при послеполетной обработке оценивать разнообразные погрешности измерения ряда основных параметров движения.
Сравнение полетных данных и смоделированных параметров полета позволяет выявить систематические погрешности различных типов: аддитивные постоянные, мультипликативные, нелинейность градуировочной характеристики. Опыт применения алгоритма показывает, что весьма эффективно выявляется наличие динамических погрешностей, в особенности сдвига по времени. Практическая значимость полученных результатов заключается в том, что указанные погрешности не обнаруживаются при простом визуальном анализе. В то же время, они могут приводить к разнообразным ошибкам при анализе полетных данных, например, при расследовании летных происшествий или при идентификации аэродинамических коэффициентов по данным летного эксперимента.
2 Программа контроля правильности бортовых измерений параметров полета
Для эффективного выявления погрешностей бортовых измерений при помощи предлагаемого алгоритма разработана специальная программа «Графический интерфейс для проверки согласованности бортовой регистрации», обеспечивающая анализ данных, формируемых алгоритмом моделирования и идентификации. Внешний вид главного окна программы представлен на рисунке 1.
При написании программы использовалась среда программирования С++ Builder 6 с компонентом TeeChartPro. В итоге системные требования к разработанной программе минимальны. Программа работает под управлением всех версий операционной системы Windows, начиная с Windows 98.
На трех вкладках «Графического интерфейса…» имеется возможность вывода ряда основных параметров полета, таких как углы тангажа, крена, атаки, скольжения, истинная воздушная скорость, угловые скорости крена, рыскания, тангажа, барометрическая высота, перегрузки и др.
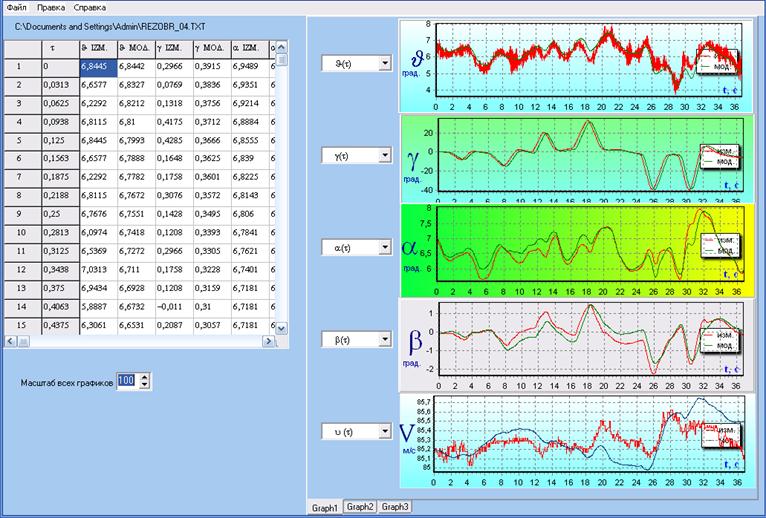
Рисунок 1 – Главное окно программы
«Графический интерфейс…» предоставляет пользователю ряд возможностей:
- отображение файла данных в виде таблицы в окне графического интерфейса;
- развертка каждого графика по отдельности на весь экран;
- изменение масштаба графиков;
- совместное отображение измеренных в полете и вычисленных в модели углов тангажа, крена, атаки, скольжения, истинной воздушной скорости в зависимости от времени и в виде графика «параметр по параметру»;
- редактирование параметров графиков (цвет и тип линии, цвет фона, параметры координатной сетки и др.);
- вывод графиков в файл и на печать;
- изменение цветовой гаммы интерфейса самой программы.
Некоторые из возможностей показаны на рисунке 2.

Рисунок 2 – Возможности «Графического интерфейса…»
3 Примеры анализа данных летных испытаний
В работе представлены результаты анализа конкретных наборов экспериментальных данных и обнаружения погрешностей различных типов.
Рассмотрим выявление погрешности типа сдвиг по времени. На рисунке 3 представлены две пары графиков, полученных с помощью программы «Графический интерфейс…» до и после коррекции с помощью рассматриваемого алгоритма.
На рисунках 3.а, 3.в представлены зависимости угла крена от времени, на рисунках 3.б, 3.г – зависимость параметр по параметру.
После коррекции наблюдается значительное улучшение сходимости измеренных и смоделированных углов крена от времени, а также стремление зависимости параметр по параметру к прямой линии. Оставшиеся флюктуации характеризуют уровень неисключенных погрешностей эксперимента.
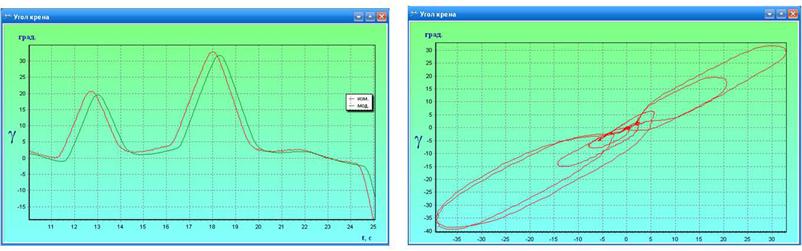
а) б)
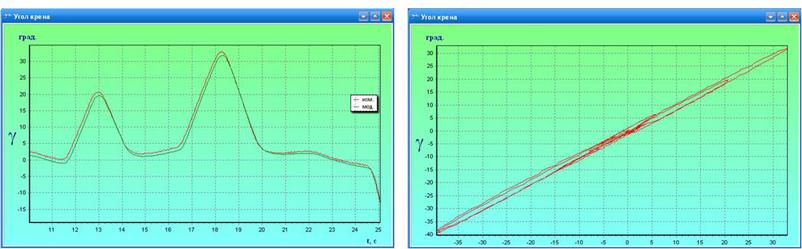
в) г)
Рисунок 3 – Выявление погрешности сдвиг по времени:
а) угол крена в зависимости от времени до ведения коррекции;
б) зависимость параметр по параметру до ведения коррекции;
в) угол крена в зависимости от времени после ведения коррекции;
г) зависимость параметр по параметру после ведения коррекции
Рассмотрим еще один пример обработки участка полета современного самолета.
Выполнялся достаточно сложный маневр типа нисходящий косой переворот, при значительном увеличении угла атаки и нормальной перегрузки. На участке возникло нештатное увеличение угла скольжения, что и определило потребность в проверке правильности системы измерений и регистрации.
На рисунке 4 представлены результаты выполнения моделирования до и после идентификации постоянных погрешностей измерений угловых скоростей и перегрузок.
В первом случае хорошо заметно, что выходные сигналы модели, вычисленные путем интегрирования уравнений движения, при увеличении времени все больше отклоняются от измеренных сигналов, что соответствует накоплению ошибок интегрирования.
Во втором случае выполнение идентификации привело к значительной коррекции погрешностей интегрирования и, соответственно, рассогласований между измерениями и сигналами модели. Однако из графиков видно, что остаются неучтенные погрешности, особенно в каналах измерений углов атаки и скольжения.

а) б)
Рисунок 4 – Результаты обработки алгоритмом моделирования:
а) до идентификации постоянных погрешностей измерений угловых скоростей и перегрузок;
б) после идентификации постоянных погрешностей измерений угловых скоростей и перегрузок
Учитывая ранее полученный опыт по оцениванию погрешностей расчета истинных углов атаки и скольжения по местным углам, измеряемым датчиками аэродинамических углов [14], была внесена нелинейная коррекция в измерения угла атаки и скорректирован масштабный коэффициент по углу скольжения.
Результаты коррекции показаны на рисунке 5. Графики показывают значительное улучшение сходимости по углам атаки и скольжения. Графики по каналам тангажа и воздушной скорости показывают, что коррекция погрешностей измерений углов атаки и скольжения улучшила сходимость и по этим сигналам.

Рисунок 5 – Результаты коррекции
Заключение
Таким образом, в результате проведенной работы:
- отработан алгоритм контроля правильности бортовых измерений основных параметров движения летательного аппарата;
- разработана программа «Графический интерфейс для проверки согласованности бортовой регистрации»;
- проведено сравнение полетных данных и смоделированных параметров полета;
- выявлены систематические погрешности различных типов: аддитивные постоянные, мультипликативные, нелинейность градуировочной характеристики;
Следует также отметить целесообразность продолжения работы по контролю правильности бортовых измерений параметров движения летательного аппарата.
Работа выполнена при поддержке Российского Фонда фундаментальных исследований (РФФИ), проект 12-08-00682.
Список литературы
1. Клюев Г.И., Макаров Н.Н., Солдаткин В.М., Ефимов И.П. Измерители аэродинамических параметров летательных аппаратов. Ульяновск: УлГТУ, 2005. 509 с.
2. Lievens K.P.A., Mulder J.A., Chu P. Single GPS Antenna Attitude Determination of a Fixed Wing Aircraft Aided with Aircraft Aerodynamics // AIAA Guidance, Navigation and Control Conference and Exhibit. San-Francisco: AIAA, 2005. P. 72-78. DOI: 10.2514/6.2005-6056
3. Пушков С.Г., Харин Е.Г., Кожурин В.Р., Ловицкий Л.Л. Технология определения аэродинамических погрешностей ПВД и воздушных параметров в летных испытаниях ЛА с использованием спутниковых средств траекторных измерений // Проблемы безопасности полетов. 2006. № 7. C. 12-19.
4. Корсун О.Н., Зиновьев А.В., Лысюк О.П., Багнюк Е.С. Алгоритм оценивания постоянной составляющей погрешности измерения воздушной скорости при учете скорости ветра // Вестник компьютерных и информационных технологий. 2008. № 9. C. 2-6.
5. Корсун О.Н., Зиновьев А.В., Лысюк О.П., Гребнев О.Н. Оценивание погрешностей измерения скорости и высоты спутниковой навигационной системой при маневрировании самолета // Проблемы безопасности полетов. 2008. № 10. C. 49-58.
6. Создание и применение математических моделей самолетов / Под ред. С.М. Белоцерковского. М.: Наука, 1984. 284 с.
7. Klein V. Estimation of Aircraft Aerodynamic Parameters from Flight Data // Progress in Aerospace Sciences. 1989. Vol. 26. P. 1-77.
8. Корсун О.Н., Лысюк О.П. Комплексная оценка погрешностей бортовых измерений в целях обеспечения задач безопасности полетов // Проблемы безопасности полетов. 2007. № 2. C. 31-41.
9. Васильченко К.К., Кочетков Ю.А., Леонов В.А. и др. Структурная идентификация математической модели движения самолета. М.: Машиностроение, 1993. 350 с.
10. Корсун О.Н. Алгоритм идентификации динамических систем с функционалом в частотной области // Автоматика и телемеханика. 2003. № 5. С. 111-121.
11. Klein V., Morelli E. Aircraft System Identification. Theory and Practice. Reston: AIAA, 2006. 484 p.
12. Аэродинамика, устойчивость и управляемость сверхзвуковых самолетов / Под ред. Г.С. Бюшгенса. М.: Наука, 1998. 811 с.
13. Maine R.E., Iliff K.W. Identification of Dynamic System. Theory and Formulation. New York: NASA, RP 1138, 1985. 138 p.
14. Корсун О.Н., Поплавский Б.К. Метод оценивания систематических погрешностей бортовых измерений углов атаки и скольжения на основе данных спутниковой навигационной системы и идентификации скорости ветра // Известия Российской академии наук. Теория и системы управления. 2011. № 1. С. 133-146.
Публикации с ключевыми словами: динамические погрешности, бортовые средства измерений, параметры полета, коррекция погрешностей измерений
Публикации со словами: динамические погрешности, бортовые средства измерений, параметры полета, коррекция погрешностей измерений
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



