научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2012
DOI: 10.7463/1112.0506146
УДК.519.24
Россия, МГТУ им. Н.Э. Баумана
Россия, МАДГТУ (МАДИ)
Введение
Адаптивный алгоритм тестового контроля предполагает, что сложность задания увеличивается в случае верного ответа, и уменьшается в случае неверного. Если предположить, что сложность может быть задана некоторым числовым значением, то в результате возможна формализация процесса тестирования в виде марковской цепи, в которой вероятности переходов по сложностям определяются на основании логистической кривой.
1 Адаптивный алгоритм тестового контроля с постоянным шагом приращения сложности
Реализация поискового алгоритма сводится к последовательному анализу локальной окрестности функционала Y, оценки градиента или направления роста и последующего перехода в другую область. Если при вычислении оценки градиента создаются помехи, то нельзя говорить о сходимости алгоритма в обычном смысле. В обычном смысле он сходиться вообще не будет, а будет “блуждать” вокруг области экстремума.
Аналогично можно поступить в случае моделирования тестового контроля. Если ответ правильный, то уровень подготовки студента выше сложности предъявленной задачи, т.е. он способен решать задачи заданной сложности. Если ответ неправильный, то - неспособен. Это подобно оценки градиента некоторой гипотетической функции регрессии, в которой градиент сам является случайной величиной.
Предлагается использовать следующий алгоритм, который весьма просто можно реализовать на практике. Обучаемый, решая задание, сталкивается с определенными трудностями. Если он решил задание, то появляется желание решить более трудное задание. Если нет - то, вернее всего, будет сделана еще одна попытка решения аналогичного по трудности задания. Если оно также не решено, то идет “откат” назад, т.е. необходимо решение задач пониженной сложности. Если сразу не решено менее сложное задание, то решается еще легче и т.д. Аналогично падению уровня сложности предъявляются задачи повышенной сложности. Если задание решено, то решается задание повышенной трудности (Рис.1).
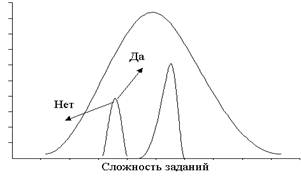
Рисунок 1 – Реализация поискового алгоритма
Таким образом, функция «уровень знаний» является преобразованием функции «сложность» задачи через «способность решения задач» определенной «сложности».
2 Марковская цепь процедуры адаптивного тестового контроля
Для формализованного представления модели тестирования будем использовать марковские цепи. Предполагается, что ответы на задания - независимые величины. Поэтому можно использовать однородную марковскую цепь, где состояниями цепи являются меры сложности заданий.
Пусть ξ=(С, P, P), где C - множество состояний марковской цепи (уровни сложности заданий); P - матрица переходных вероятностей P=||pij||; P - вектор-строка начального распределения сложностей P=||pi||. Диаграмма переходов приведена на рисунке 2.

Рисунок 2 – Диаграмма переходов марковской цепи
Каждому состоянию Ci соответствует уровень сложности βi. Переходные вероятности определяются естественным образом на основании логистической кривой:
Для данной цепи существует единственное, не зависящее от начального состояния, стационарное распределение. Обозначим стационарные вероятности состояний Ci за πi. При этих обозначениях вектор-строка стационарных вероятностей определяется равенством:
| (3) |
Эти вероятности являются решением системы уравнений:
| (4) |
Решение этой системы уравнений методом индукции дает результат:
| (5) |
которое после соответствующих преобразований приводится к соотношению:
Это стационарное распределение получено на основании введения некоторой дискретизации в пространстве «сложности».
3 Сходимость стационарных вероятностей при увеличении дискретизации шкалы уровня сложности
В работе поставлена задача увеличения дискретизации уровня сложности на той же шкале. Предполагается, что существует некоторая гипотетическая функция уровня знаний, положение которой мы должны найти. ΔX - приращение сложности (в бальной шкале). ∇Y - градиент «знаний» в некотором универсальном множестве, в качестве оценки которого используется приращение функционала Y в локальной окрестности (∆Y).
Показано, что для дискретного распределения π(Ci) может быть использовано приближение:
где a - нормирующий множитель.
В итоге получено общее выражение для вычисления стационарного распределения значений управляемого параметра. В практике моделирования наиболее часто оценки имеют либо постоянную дисперсию, либо постоянный коэффициент вариации. Поэтому рассмотрены частные случаи.
4 Постоянная дисперсия оценки
Предположим, что для всех значений управляемого параметра дисперсия оценки имеет вид ∀C∈CCC σ(C)=σ=Const. Тогда:
В этом случае выражение для плотности вероятности может быть представлено в следующем виде:
| (9) |
Вводя обозначение, независящее от X, перепишем формулу в виде:
| (10) |
Так как экспоненциальная функция монотонно возрастающая, то большим значениям целевой функции соответствуют большие значения плотности распределения Ws(x). Соответственно максимум плотности приходится на максимум целевой функции.
В таблице 1 приведены значения плотности распределения Ws(x) при различных s для целевой функции:
Чем меньше дисперсия, тем более выражено значение максимума. Так, например, для σ=0.1 модель будет пребывать 90 % всего времени в интервале (3.0, 7.0), содержащем значение максимума.
Таблица 1 – Значения плотности распределения
X | W(x)/W(x*) | Y(x) | |||
σ=0.1 | σ=0.25 | σ=0.5 | σ=1.0 | ||
5.0 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
6.0 | 0.666 | 0.850 | 0.922 | 0.960 | 0.964 |
7.0 | 0.197 | 0.522 | 0.725 | 0.850 | 0.856 |
8.0 | 0.020 | 0.232 | 0.481 | 0.696 | 0.676 |
9.0 | 0.002 | 0.074 | 0.273 | 0.522 | 0.424 |
10.0 | 4×10-5 | 0.017 | 0.131 | 0.362 | 0.100 |
5 Оценка с постоянным коэффициентом вариации
Предположим, что для всех значений:
| (12) |
Значение интеграла в формуле (7) для плотности вероятности в данном случае приводится к виду:
| (13) |
Отсюда получим следующее выражение:
В данном случае целевая функция может быть только положительной величиной. При γ=1 функция плотности вероятности с точностью до постоянного множителя на всем пространстве X совпадает с математическим ожиданием оценки функционала. Чем меньше коэффициент вариации, тем более выражен максимум плотности вероятности.
6 Оценка эффективности алгоритма с постоянным шагом
При постоянной длине шага исследовались характеристики блуждания в окрестности экстремума управляемого параметра. С целью исключения влияния начального этапа процесса управления, отбрасывалось 10 начальных значений. Получены статистики блуждания на оси сложности заданий (Рис. 3).
Таким образом, алгоритм управления с постоянным шагом выводит нас в окрестность истинного значения корня стохастического уравнения для определения истинного уровня.
Проведен сравнительный анализ предложенного алгоритма с алгоритмом статического предъявления. В таблице 2 приведена матрица классификации, полученная на основе имитационного эксперимента, для теста семиуровневой сложности по пять заданий на каждом уровне сложности.
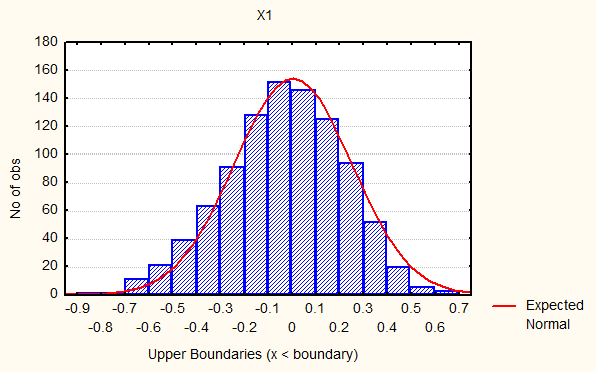
Рисунок 3 – Распределение сложности при постоянной длине шага
Таблица 2 – Статический план теста по 5 задач каждой сложности
Класс | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
1 | 0,822 | 0,155 | 0,002 | 0,000 | 0,000 | 0,000 | 0,000 |
2 | 0,176 | 0,700 | 0,125 | 0,000 | 0,000 | 0,000 | 0,000 |
3 | 0,002 | 0,145 | 0,775 | 0,185 | 0,002 | 0,000 | 0,000 |
4 | 0,000 | 0,000 | 0,097 | 0,636 | 0,100 | 0,000 | 0,000 |
5 | 0,000 | 0,000 | 0,001 | 0,179 | 0,757 | 0,152 | 0,002 |
6 | 0,000 | 0,000 | 0,000 | 0,000 | 0,139 | 0,686 | 0,169 |
7 | 0,000 | 0,000 | 0,000 | 0,000 | 0,002 | 0,162 | 0,829 |
Для адаптивного алгоритма при том же общем количестве заданий (35) на основе той же модели получены результаты, приведенные в таблице 3.
Анализ таблиц позволяет сделать вывод, что классификация на основе адаптивного алгоритма дает лучшие результаты для всех уровней подготовленности испытуемых. В девяти уровневой модели знаний адаптивный алгоритм дает еще больший выигрыш по классификации. Однако при малом количестве уровней выигрыш становится незначительным.
Таблица 3 – Адаптивный план теста при NT=35
Класс | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
1 | 0,906 | 0,085 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
2 | 0,094 | 0,821 | 0,090 | 0,000 | 0,000 | 0,000 | 0,000 |
3 | 0,000 | 0,094 | 0,818 | 0,098 | 0,000 | 0,000 | 0,000 |
4 | 0,000 | 0,000 | 0,092 | 0,803 | 0,090 | 0,000 | 0,000 |
5 | 0,000 | 0,000 | 0,000 | 0,099 | 0,813 | 0,102 | 0,000 |
6 | 0,000 | 0,000 | 0,000 | 0,000 | 0,097 | 0,804 | 0,090 |
7 | 0,000 | 0,000 | 0,000 | 0,000 | ,002 | ,0904 | ,910 |
Заключение
Таким образом, предлагаются механизмы формирования адаптивных тестов с возможностью оценки их эффективности с точки зрения вероятностей ошибочных классификаций. Сформированы общие принципы разработки адаптивных механизмов предъявления тестовых заданий и формирования моделей их поведения. Построена формализованная модель процедуры адаптивного тестового контроля в виде марковской цепи. На основе имитационных экспериментов проведен сравнительный анализ сходимости алгоритмов оценивания, получены количественные оценки и показана эффективность разработанных алгоритмов. Проведенные имитационные эксперименты подтвердили высокую эффективность разработанных адаптивных алгоритмов.
Список литературы
1. Соловов А.В. Электронное обучение: проблематика, дидактика, технология. Самара: «Новая техника», 2006. 464 с.
2. Норенков И.П., Зимин А.М. Информационные технологии в образовании. М.: Изд-во МГТУ им. Н.Э.Баумана, 2004. 352 с.
3. Норенков И.П. Технологии разделяемых единиц контента для создания и сопровождения информационно-образовательных сред // Информационные технологии. 2003. № 8. С. 34-40.
4. Оганесян А.Г. Опыт компьютерного контроля знаний // Дистанционное образование. 1999. № 6. С. 30-35.
5. Челышкова М.Б. Теория и практика конструирования педагогических тестов: учеб. пособие. М.: Логос, 2002. 432 с.
6. Booch G.., Jacobson I., Rumbaugh J. The Unified Modeling Language for Object-Oriented Development. Documentation Set Version 1.1. September 1997.
Публикации с ключевыми словами: тестовый контроль, эффективность, марковские цепи, адаптивность, сложность задания, сходимость алгоритма
Публикации со словами: тестовый контроль, эффективность, марковские цепи, адаптивность, сложность задания, сходимость алгоритма
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||
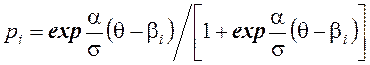 ,
,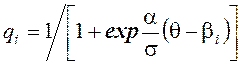 ,
, .
. ,
,  ,
, .
.

 .
.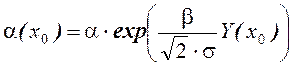 .
. .
.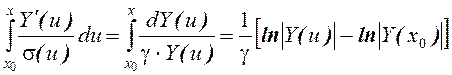 .
.



