научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2012
DOI: 10.7463/1212.0506112
УДК 621.31
Россия, МГТУ им. Н.Э. Баумана
sa_vasyukov@mail.ru
Пространственное положение оси вращения разбалансированного ротора ЭСГ относительно положительного направления трех осей чувствительности емкостных датчиков устанавливается тремя углами![]() , связанными между собой системой трех уравнений вида [1]:
, связанными между собой системой трех уравнений вида [1]:
 (1)
(1)
Эта система, в принципе, позволяет при известных значениях углов ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() определить неизвестные три угла
определить неизвестные три угла ![]() ,
, ![]() ,
,![]() , составляемых осью вращения ротора с тремя осями чувствительности O1, O2, O3.
, составляемых осью вращения ротора с тремя осями чувствительности O1, O2, O3.
Для однозначного определения произвольной угловой ориентации оси вращения ротора в диапазоне 0-360° система уравнений функциональной связи [1] должна обеспечивать однозначную функциональную связь входящих в нее геометрических углов ![]() ,
, ![]() ,
,![]() . В то же время при выводе основных уравнений связи на область допустимых значений углов
. В то же время при выводе основных уравнений связи на область допустимых значений углов ![]() , фиксирующих угловую ориентацию оси вращения ротора, было наложено ограничение (1.8), устанавливающее, что ось вращения не совпадает и не перпендикулярна ни одной из осей чувствительности ротор-электродных пар. Очевидно, что при угловых перемещениях оси вращения в широком диапазоне углов возможны и такие ее положения, когда наложенное ограничение не удовлетворяется, во всяком случае, для одной из осей чувствительности.
, фиксирующих угловую ориентацию оси вращения ротора, было наложено ограничение (1.8), устанавливающее, что ось вращения не совпадает и не перпендикулярна ни одной из осей чувствительности ротор-электродных пар. Очевидно, что при угловых перемещениях оси вращения в широком диапазоне углов возможны и такие ее положения, когда наложенное ограничение не удовлетворяется, во всяком случае, для одной из осей чувствительности.
От указанного недостатка свободна октантная система электродов подвеса [12], в которой оси чувствительности ротор-электродных пар совпадают с диагоналями куба с вершинами в центрах электродов подвеса (рис. 1).
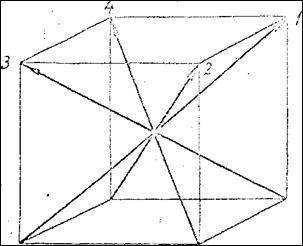
Рисунок 1.
В результате очевидных тригонометрических вычислений можно показать, что для октантной системы электродов подвеса взаимное расположение положительных направлений осей чувствительности ротор-электродных пар характеризуется следующими количественными соотношениями:

Тогда система уравнений функциональной связи вида (1) относительно углов, составляемых осью вращения ротора, например с положительными направлениями осей 1, 2 и 3, будет иметь следующий вид:
 (2)
(2)
Обозначив ![]() , перепишем систему (2) в виде:
, перепишем систему (2) в виде:
 (3)
(3)
Разрешив уравнения системы (3) относительно D2, D3, D1соответственно, получим следующие алгебраические выражения:
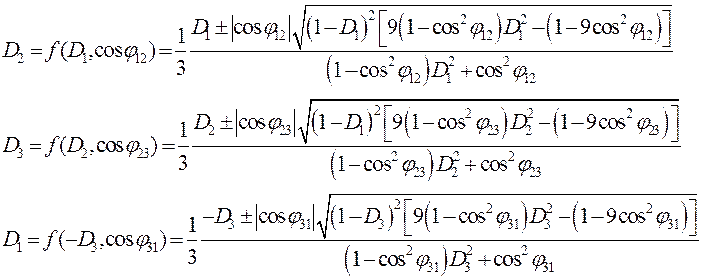 (4)
(4)
Рассматривая первое из полученных алгебраических выражений при ![]() и выполнив его дифференцирование по аргументу, а затем, приравняв получившееся выражение поочередно нулю и бесконечности, найдем координаты характерных точек функции
и выполнив его дифференцирование по аргументу, а затем, приравняв получившееся выражение поочередно нулю и бесконечности, найдем координаты характерных точек функции![]() рис. 2
рис. 2
 (5)
(5)
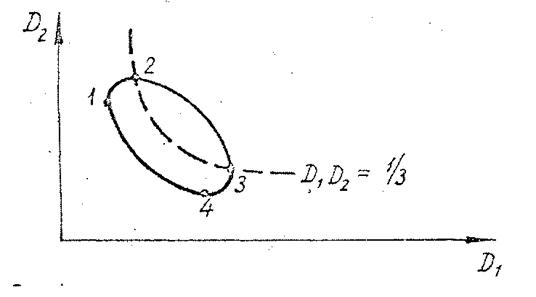
Рисунок 2.
Возвращаясь к первому уравнению системы (2), можно отметить, что в случае, если ![]() имеет место D1D2≥1/3 и, следовательно, точка решения
имеет место D1D2≥1/3 и, следовательно, точка решения ![]() лежит на участке 2-3 (рис. 2), в противном случае — на участке 2-1 — 4-3. Выполнив соответствующие алгебраические преобразования и при
лежит на участке 2-3 (рис. 2), в противном случае — на участке 2-1 — 4-3. Выполнив соответствующие алгебраические преобразования и при![]() , также получим координаты характерных точек функции
, также получим координаты характерных точек функции![]() , рис. 3
, рис. 3
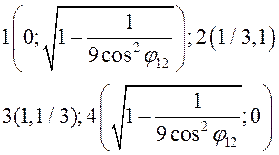
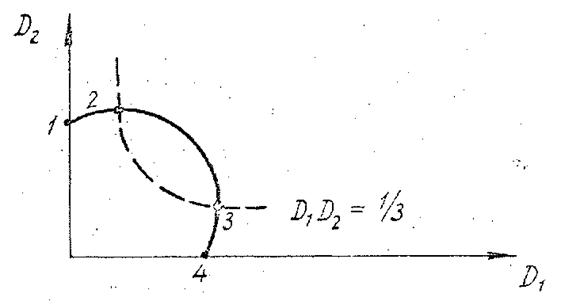
Рисунок 3.

Рисунок 4.
В этом случае также справедливо утверждение, что при![]() точка решения лежит на участке 2-3, в противном случае — на участках 1-2 или 3-4. Поскольку функция
точка решения лежит на участке 2-3, в противном случае — на участках 1-2 или 3-4. Поскольку функция ![]() идентична функции
идентична функции ![]() вычисление координат ее характерных точек приводит к аналогичным выражениям с теми же замечаниями к области нахождения точки решения
вычисление координат ее характерных точек приводит к аналогичным выражениям с теми же замечаниями к области нахождения точки решения ![]() .
.
Рассматривая третье уравнение системы (2), можно отметить, что вследствие имеющего место неравенства D3D1 ≥ 0, для того, чтобы это уравнение могло обратиться в тождество, должно иметь место![]() , а, следовательно, график функции
, а, следовательно, график функции ![]() аналогичен графику функции
аналогичен графику функции ![]() (рис. 3) в области отрицательного аргумента (-D3)с соответствующими алгебраическими выражениями для координат характерных точек кривой
(рис. 3) в области отрицательного аргумента (-D3)с соответствующими алгебраическими выражениями для координат характерных точек кривой![]() .
.
Таким образом, анализ функциональных зависимостей системы (4) показал, что соответствующие функции являются непрерывными и монотонными на участках их изменения, вследствие чего функциональное уравнение вида х = F(x), где х и F(x), в частности, могут быть равны соответственно D и ![]() имеет решение и притом единственное, которое может быть найдено с необходимой точностью одним из численных итерационных методов решения функциональных уравнений вида х = F(x). В результате численного решения функционального уравнения определяются две из трех необходимых точек решения (в частности
имеет решение и притом единственное, которое может быть найдено с необходимой точностью одним из численных итерационных методов решения функциональных уравнений вида х = F(x). В результате численного решения функционального уравнения определяются две из трех необходимых точек решения (в частности ![]() и
и ![]() ), а после преобразования в одной из двух оставшихся координатных плоскостей находится и последняя точка решения
), а после преобразования в одной из двух оставшихся координатных плоскостей находится и последняя точка решения ![]() .
.
При перемещениях оси вращения ротора в широком диапазоне углов возможно ее совпадение с одной из осей чувствительности (для определенности будем считать, что ось вращения совпала с положительным направлением 1-ой оси чувствительности). В этом случае для определения трех углов ![]() , фиксирующих пространственную ориентацию оси вращения ротора, уравнения связи можно составить для углов, образуемых осью вращения ротора с положительными направлениями 2 и 4 осей чувствительности и отрицательным направлением 3-ей оси. Соответствующая этому случаю, система уравнений связи будет иметь вид:
, фиксирующих пространственную ориентацию оси вращения ротора, уравнения связи можно составить для углов, образуемых осью вращения ротора с положительными направлениями 2 и 4 осей чувствительности и отрицательным направлением 3-ей оси. Соответствующая этому случаю, система уравнений связи будет иметь вид:
 (5)
(5)
Под![]() в данном случае понимается угол, составляемый осью вращения ротора с отрицательным направлением 3-ей оси чувствительности. Система уравнений (5) в результате аналогичных, выполненных выше, преобразований может быть приведена к совокупности алгебраических выражений вида
в данном случае понимается угол, составляемый осью вращения ротора с отрицательным направлением 3-ей оси чувствительности. Система уравнений (5) в результате аналогичных, выполненных выше, преобразований может быть приведена к совокупности алгебраических выражений вида
![]() (6)
(6)
где ![]()
Примерный вид каждой из зависимостей (6), построенной с учетом того, что в данном случае![]() , приведен на рис. 4, где координаты точек 1 и 2 соответствуют координатам точек 1 и 4 на рис. 3. Анализируя зависимости (6), можно также утверждать, что функции f в рассматриваемом случае непрерывны и монотонны в интервалах их изменения, а поэтому так же функциональное уравнение х = F(x), соответствующее любой из функциональных зависимостей системы (6), имеет единственное решение, которое может быть найдено одним из сходящихся итерационных методов решения функционального уравнения х = F(x).
, приведен на рис. 4, где координаты точек 1 и 2 соответствуют координатам точек 1 и 4 на рис. 3. Анализируя зависимости (6), можно также утверждать, что функции f в рассматриваемом случае непрерывны и монотонны в интервалах их изменения, а поэтому так же функциональное уравнение х = F(x), соответствующее любой из функциональных зависимостей системы (6), имеет единственное решение, которое может быть найдено одним из сходящихся итерационных методов решения функционального уравнения х = F(x).
Таким образом, при любой угловой ориентации оси вращения ротора относительно осей чувствительности четырехосной (октантной) системы электродов подвеса, три угла ![]() , могут быть однозначно определены в результате численного решения соответствующей системы трех трансцендентных уравнений функциональной связи. Очевидно, что для решения такой системы уравнений должны быть также известны значения всех других углов, входящих в систему, а именно: углов совокупности
, могут быть однозначно определены в результате численного решения соответствующей системы трех трансцендентных уравнений функциональной связи. Очевидно, что для решения такой системы уравнений должны быть также известны значения всех других углов, входящих в систему, а именно: углов совокупности ![]() и
и ![]() . Как уже отмечалось, совокупность геометрических углов
. Как уже отмечалось, совокупность геометрических углов ![]() определяется исключительно конструкцией прибора (взаимным расположением осей симметрии ротор — электродных пар) и является постоянной, не зависящей от угловой ориентации оси вращения ротора, а элементы этой совокупности углов войдут в соответствующую систему уравнений связи в качестве постоянных. В то же время совокупность углов
определяется исключительно конструкцией прибора (взаимным расположением осей симметрии ротор — электродных пар) и является постоянной, не зависящей от угловой ориентации оси вращения ротора, а элементы этой совокупности углов войдут в соответствующую систему уравнений связи в качестве постоянных. В то же время совокупность углов ![]() не является постоянной, а трансформируется в зависимости от положения экваториальной плоскости ротора и, соответственно, оси вращения ротора, Таким образом в данном случае для определения мгновенного углового положения оси вращения ротора в косоугольной системе координат (мгновенных значений, по крайней мере, трех углов
не является постоянной, а трансформируется в зависимости от положения экваториальной плоскости ротора и, соответственно, оси вращения ротора, Таким образом в данном случае для определения мгновенного углового положения оси вращения ротора в косоугольной системе координат (мгновенных значений, по крайней мере, трех углов ![]() ) необходимо измерить функционально связанные с ним три угла
) необходимо измерить функционально связанные с ним три угла ![]() .
.
Естественно принять, что система измерения этих углов должна органически вписываться в конструкцию ЭСГ и, что особенно важно, осуществлять измерение с помощью бесконтактных датчиков. В [1] изложен принцип кодирования угловых перемещений оси вращения ротора посредством эффекта модуляции зазора электрод — ротор, вызванного вращением разбалансированного ротора, поэтому логично было использовать бесконтактный емкостной датчик линейных перемещений, уже нашедший применение в конструкции ЭСГ в системе подвеса ротора. В новых условиях на его выходе появится напряжение биения на частоте вращения ротора, параметры которого будут содержать информацию об его угловых перемещениях (формула 1.4). Там же указано, что измерение геометрических углов ![]() - между проекциями каких-либо двух осей чувствительности Oi, и Oj, электродных пар на экваториальную плоскость ротора может быть осуществлено посредством измерения временных интервалов между экстремумами линейных перемещений ротора в направлении этих осей (формула 1.3). Таким образом окончательно можно сделать вывод о том, что геометрический угол
- между проекциями каких-либо двух осей чувствительности Oi, и Oj, электродных пар на экваториальную плоскость ротора может быть осуществлено посредством измерения временных интервалов между экстремумами линейных перемещений ротора в направлении этих осей (формула 1.3). Таким образом окончательно можно сделать вывод о том, что геометрический угол ![]() численно равен разности фаз между напряжениями биений на выходе соответствующих датчиков линейных перемещений ротора, то есть
численно равен разности фаз между напряжениями биений на выходе соответствующих датчиков линейных перемещений ротора, то есть
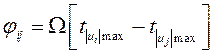 (7)
(7)
где ![]() — моменты времени, в которые напряжения биений на выходе датчиков линейных перемещений ротора по i-ой и j-ой осям чувствительности соответственно достигают своих экстремальных значений.
— моменты времени, в которые напряжения биений на выходе датчиков линейных перемещений ротора по i-ой и j-ой осям чувствительности соответственно достигают своих экстремальных значений.
Выводы: Анализ уравнений функциональной связи в ЭСГ указывает на возможность вычисления неизвестных углов, составляемых осью вращения ротора с осями чувствительности в пространственно-фазовом методе при ограничении, что ось вращения не совпадает и не перпендикулярна ни одной из осей чувствительности. Для однозначного определения произвольной ориентации оси вращения ротора в диапазоне 0÷360°, когда такая ситуация может быть, необходимо перейти к четырехосной (октантной) системе осей чувствительности.
Список литературы:
1. Дробышев Г.Ф. Принцип кодирования угловых перемещений в системах с несбалансированным ротором // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2011. Спец. вып. «Электротехника и электроника». С. 95-101.
2. Avionics. Light Compact Navigator // Aviation Week & Space Technology. 1970. No 9. P. 51-55.
Публикации с ключевыми словами: электростатический подвес, электростатический гироскоп (ЭСГ), разбалансированный ротор, уравнения функциональной связи, октантная система координат
Публикации со словами: электростатический подвес, электростатический гироскоп (ЭСГ), разбалансированный ротор, уравнения функциональной связи, октантная система координат
Смотри также:
- О влиянии законов управления потенциалами на силовые характеристики сферического электростатического подвеса
- Об одном способе повышения стабильности центрирования ротора электростатического подвеса
- Об одном способе улучшения статической и динамической равножесткости в трехосном электростатическом подвесе
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



