научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2012
DOI: 10.7463/1112.0500490
УДК 778.35:629.7
Россия, МГТУ имени Н.Э. Баумана
Россия, ОАО «Камов»
Россия, ВУНЦ ВВС «Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина»
vesel_foto@mail.ru
Введение
Эффективность применения современных беспилотных летательных аппаратов (БЛА) против террористических, контрабандных, наркотических и других угроз, связанных с несанкционированным проникновением на охраняемые территории во многом зависит от качества систем наблюдения, сбора и обработки информации, управления и контроля, а также систем принятия решений. В качестве одной из основных систем сбора и обработки информации на борту БЛА используется оптико-электронная система (ОЭС). Проектирование ОЭС БЛА должно исходить из требований, предъявляемых условиями применения БЛА, комплексом алгоритмов, подлежащих реализации на борту БЛА, точностью представления входной и выходной информации, а также динамикой управления БЛА. Задача распознавания изображений наземных объектов в БЛА является ключевой для приближения БЛА к возможностям пилотируемой авиации. Эффективное решение указанной задачи повышает вероятность обнаружения наземных объектов с использованием ОЭС.
Успешность выполнения задачи распознавания сложных трехмерных объектов по их двумерному изображению, формируемому ОЭС, характеризуется показателями эффективности. В большинстве систем технического зрения в качестве показателей используются вероятность правильного распознавания (классификации) или достоверность распознавания. Очевидно, что показатели эффективности зависят от дальности, маскировки, метеоусловий и целого ряда случайных факторов. Поскольку при измерениях сигнала от регистрирующего датчика (тепловизора, телекамеры или фотокамеры) возникают шумы, измеряемые величины носят случайный характер. Случайные факторы можно в зависимости от причин их возникновения разделить на группы. Первая группа факторов определяется самим излучающим или отражающим объектом: характером отражения и рассеивания сигнала от его поверхности. Ввиду структурной сложности изображений наземного объекта, многовариантности его ракурсов, окрасок, наконец, внешнего оборудования и средств маскировки эта группа имеет детерминированную и случайную составляющие. Вторая группа связана с воздействием среды на формирование изображения и описывается характером рассеивания (поглощения) оптического излучения в атмосфере. Оно зависит от метеоусловий, наличия турбулентности и тепловых потоков в атмосфере на участке луча “БЛА - объект”. Третья группа случайных факторов связана с приемником изображения ОЭС. Здесь происходит оцифровка изображения - квантование по уровню яркости сигнала и квантование в пространстве. В процессе квантования вносятся погрешности, обусловленные чувствительностью элементов матрицы приемника оптического излучения и конечными размерами каждого элемента. К этой же группе относятся помехи: естественные (ракурс солнца, зеленые насаждения, блики от водных поверхностей, стекла, крыш и других поверхностей) и искусственные (ослепление лазерами и другими мощными источниками).
Особенностями ОЭС БЛА, отличающими их от других систем технического зрения, являются: устойчивость к высокому уровню помех, обусловленных нестационарными условиями экспозиции сцены; работа в условиях реального времени; ограничения на вычислительные ресурсы и ресурсы энергоснабжения. Особо следует выделить возможность адаптации ОЭС к новым объектам, хотя обычно ОЭС работают по образцу. В этой связи, работу системы технического зрения можно рассматривать на 2 этапах:
− проектирование и первичное обучение,
− эксплуатация и дообучение с целью распознавания новых объектов.
Рассмотрим некоторые принципы построения систем технического зрения БЛА, которые закладываются на первом этапе и определяют потенциальные возможности по распознаванию наземных объектов. Общая схема решения задачи распознавания приведена на рисунке 1.
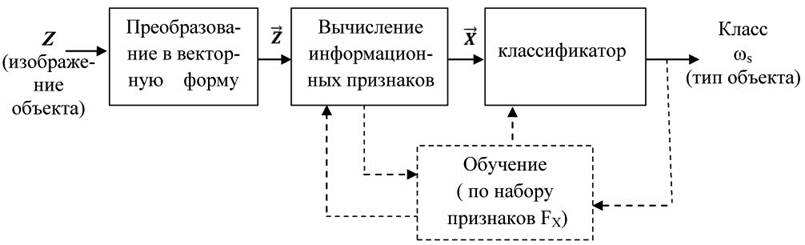
Рисунок 1 – Схема решения задачи распознавания
Изображение цели, сформированное в фокальной плоскости оптическим каналом и оцифрованное матричным приемником ОЭС, будем обозначать Z. По-существу, Z представляет собой двумерную матрицу размером N´M (размер фотоприемника в пикселях). Последовательно считывая строки матрицы Z, преобразуем её в вектор ![]() размерности M´N. Вектор
размерности M´N. Вектор ![]() будем называть образом наблюдаемого объекта Z. Будем считать, что образ объекта может принадлежать к классу ωs множества классов целей 𝛀={ωs, s=1…K}. Множество 𝛀 счетно. Каждый класс определяется конкретной моделью объекта. Алгоритм соотнесения образа объекта к одному из классов wsбудем называть классификатором. Образу
будем называть образом наблюдаемого объекта Z. Будем считать, что образ объекта может принадлежать к классу ωs множества классов целей 𝛀={ωs, s=1…K}. Множество 𝛀 счетно. Каждый класс определяется конкретной моделью объекта. Алгоритм соотнесения образа объекта к одному из классов wsбудем называть классификатором. Образу ![]() в L-мерном метрическом пространстве признаков соответствует вектор
в L-мерном метрическом пространстве признаков соответствует вектор ![]() Из рисунка 1 видно, что выбор информационных признаков перед первичным обучением системы технического зрения, после обучения имеет определяющее влияние на эффективность процесса распознавания наземного объекта.
Из рисунка 1 видно, что выбор информационных признаков перед первичным обучением системы технического зрения, после обучения имеет определяющее влияние на эффективность процесса распознавания наземного объекта.
В качестве признаков, как правило, выбирают следующие признаки изображения:
− геометрические (отрезки прямых, дуги – обобщенный метод Хафа, детекторы углов –Харриса, Томаши, контуры и другие особенности изображения);
− спектральные (спектральные характеристики на основе Фурье или вейвлет преобразования);
− структурные (на основе морфологического анализа и других методов);
− энергетические или яркостные;
− статистические (на основе анализа распределений и статистик).
Без ограничения общности могут быть использованы любые признаки и их комбинации для обучения системы технического зрения. Будем предполагать, что при фиксированном выборе векторного пространства признаков классификатор обеспечивает оптимальное решение по распознаванию.
Постановка задачи.
Выбор наиболее информативных признаков, описывающих множество классов объектов Ω={𝜔j, j=1…K}, является ключевым моментом в задаче распознавания сложных по форме, спектру и другими признакам объектов. Требуется сформулировать принципы отбора информационных признаков образов, обеспечивающих решение задачи распознавания образов из K классов по критерию максимума вероятности распознавания ![]() заданным набором
заданным набором ![]() любого объекта из K классов. Классы wj и wi являются не пересекающимися: если
любого объекта из K классов. Классы wj и wi являются не пересекающимися: если ![]() и
и ![]() , то следует
, то следует ![]() .
.
Допущения:
1 в кадре присутствует информация только об одном нормализованном образе;
2 векторы признаков ![]() для всех классов имеют одинаковый закон распределения.
для всех классов имеют одинаковый закон распределения.
Разделимость классов с точки зрения теории информации
Для оценки информативности признаков воспользуемся положениями теории информации - используем понятия объем информации ![]() и энтропия
и энтропия ![]() . Ральф Хартли в работе [1] предложил объем информации
. Ральф Хартли в работе [1] предложил объем информации ![]() , содержащийся в образе и связанный с реализацией события
, содержащийся в образе и связанный с реализацией события ![]() с вероятностью pk, определять как логарифмическую функцию:
с вероятностью pk, определять как логарифмическую функцию:
![]() (1)
(1)
где основание логарифма, как правило, равно 2 (единица информации - bit) или e (единица информации - nat). Для определенности в работе выбрана единица e. Ввиду того, что разрешение приемника ОЭС определено – M´N, тогда множество реализаций события ![]() – счетно и ограничивается условием:
– счетно и ограничивается условием:
![]() .
.
Здесь предполагается, что минимальный объем информации соответствует достоверному событию (![]() , а максимальный соответствует событию с наибольшей неопределенностью - реализация образа в виде 1 точки
, а максимальный соответствует событию с наибольшей неопределенностью - реализация образа в виде 1 точки![]() .
.
В работе Клода Шеннона [2] введено среднее значение объема информации![]() при всех возможных реализациях образа называемое энтропией
при всех возможных реализациях образа называемое энтропией ![]() :
:
![]() (2)
(2)
Считая, что 0×log0=0 для энтропии ![]() получим диапазон:
получим диапазон:
![]() .
.
Прежде чем приступить к решению задачи по выбору наиболее информативных признаков ответим на вопрос: какой из двух наборов признаков FX и GYс распределениями ![]() ,
, ![]() несет больший объем информации об образе? Здесь
несет больший объем информации об образе? Здесь ![]() - гауссово L-мерное распределение случайного вектора признаков
- гауссово L-мерное распределение случайного вектора признаков![]() ,
, ![]() – отличное от гауссового L-мерное распределение случайного вектора признаков
– отличное от гауссового L-мерное распределение случайного вектора признаков ![]() . Распределения
. Распределения ![]() ,
, ![]() имеют одинаковые значения первого и второго статистических моментов.
имеют одинаковые значения первого и второго статистических моментов.
В работе [3] был сформулирован принцип максимальной энтропии: “Если выводы основываются на неполной информации, она должна выбираться из распределения вероятности, максимизирующего энтропию при заданных ограничениях на распределение”. В [4] доказано, что принцип максимальной энтропии корректен и существует только одно распределение, обеспечивающее максимум энтропии, которое можно выбрать с помощью "аксиом согласованности":
− уникальность (результат должен быть единственным);
− инвариантность (выбор системы координат не должен влиять на результат);
− независимость системы (не должно иметь значения, будет ли независимая информация о независимых системах браться в расчет как в терминах различных плотностей раздельно, так и вместе, в терминах совместной плотности);
− независимость подмножеств (не должно иметь значения, будет ли независимое множество состояний системы рассматриваться в терминах условной плотности или полной плотности системы).
Для случая многомерного гауссового распределения ![]() центрированного вектора признаков
центрированного вектора признаков ![]() известно выражение[7]:
известно выражение[7]:

Тогда доопределим энтропию для непрерывного вектора признаков ![]() следующим выражением [7]:
следующим выражением [7]:
![]() . (2б)
. (2б)
Последняя величина получается из (2) как предельный переход по количеству состояний для вектора признаков ![]() и в литературе носит название дифференциальной энтропии. Поскольку на практике, как правило, используется квантованная оценка признаков и выборочные оценки вектора математического ожидания и матрицы ковариации, то нас будет интересовать только вывод некоторых выражений для оценки энтропии с переходом к дискретному представлению. Подставляя выражение (2а) в интеграл (2б), для многомерного гауссового распределения
и в литературе носит название дифференциальной энтропии. Поскольку на практике, как правило, используется квантованная оценка признаков и выборочные оценки вектора математического ожидания и матрицы ковариации, то нас будет интересовать только вывод некоторых выражений для оценки энтропии с переходом к дискретному представлению. Подставляя выражение (2а) в интеграл (2б), для многомерного гауссового распределения ![]() получено выражение для энтропии
получено выражение для энтропии ![]() :
:
![]() , (3)
, (3)
где L - размерность вектора признаков ![]() - матрица ковариации случайного вектора признаков
- матрица ковариации случайного вектора признаков ![]() ,
, ![]() - определитель матрицы
- определитель матрицы![]() . Из (3) вытекает 2 вывода.
. Из (3) вытекает 2 вывода.
1. Если вектор признаков ![]() описывается гауссовой статистикой, то энтропия ее имеет наибольшее значение среди прочих векторов признаков
описывается гауссовой статистикой, то энтропия ее имеет наибольшее значение среди прочих векторов признаков ![]() , описываемых иной статистикой с таким же вектором средних значений, при этом выполняется неравенство:
, описываемых иной статистикой с таким же вектором средних значений, при этом выполняется неравенство: ![]() , причем равенство достигается только при совпадении распределений
, причем равенство достигается только при совпадении распределений ![]() и
и ![]() .
.
2. Энтропия ![]() гауссового случайного вектора признаков
гауссового случайного вектора признаков ![]() однозначно определяется его ковариационной матрицей
однозначно определяется его ковариационной матрицей ![]() и не зависит от среднего значения вектора признаков
и не зависит от среднего значения вектора признаков ![]() .
.
На основании сделанных выводов может быть сформулирован первый принцип: в соответствии с принципом максимальной энтропии считаем, что вектор признаков ![]() описывается гауссовой статистикой.
описывается гауссовой статистикой.
Поскольку энтропия ![]() для наиболее информативного набора признаков
для наиболее информативного набора признаков ![]() образа определяется его ковариационной матрицей
образа определяется его ковариационной матрицей ![]() , то учитывая ее симметричный характер можно использовать разложение Карунена-Лоева [5]:
, то учитывая ее симметричный характер можно использовать разложение Карунена-Лоева [5]:
![]() (4)
(4)
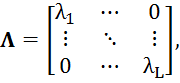
где ![]() - диагональная матрица состоящая из собственных значений
- диагональная матрица состоящая из собственных значений ![]() , а
, а![]() - матрица составленная из столбцов – собственных векторов, соответствующих
- матрица составленная из столбцов – собственных векторов, соответствующих ![]() . Заметим что ранг матрицы
. Заметим что ранг матрицы![]() т.е.
т.е. ![]() определяет количество линейно независимых векторов признаков, отвечающих за классификацию
определяет количество линейно независимых векторов признаков, отвечающих за классификацию ![]() . Выполняя процедуру нормализации для собственных значений и собственных векторов
. Выполняя процедуру нормализации для собственных значений и собственных векторов![]() , получим нормализованные собственные значения
, получим нормализованные собственные значения ![]() :
:

Учитывая тот факт, что ![]() соответствует ортогональному преобразованию, т.е.
соответствует ортогональному преобразованию, т.е. ![]() , для
, для ![]() получим:
получим:

Подставляя выражение (5) в (3), получим:
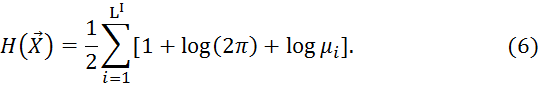
В работе [5] показано, что максимальная погрешность разложения (4) определяется выражением:
![]()
В (7) предполагается, что все собственные значения и их собственные вектора упорядочены в порядке убывания, так как значимость каждого компонента вектора признаков ![]() определяется его собственным значением:
определяется его собственным значением:
![]()
![]() . (7а)
. (7а)
Сформулируем второй принцип: собственные значения разложения Карунена-Лоева (7а), упорядоченные в порядке убывания, определяют информационную значимость соответствующей компоненты вектора признаков ![]() .
.
Рассмотрим ортогональное преобразование исходного вектора признаков![]() :
:
![]() ,
, ![]()
![]() ,
, ![]() , (8)
, (8)
т.е. матрица![]() состоит из LI линейно независимых векторов-столбцов (
состоит из LI линейно независимых векторов-столбцов (![]() и эти столбцы ортонормированны:
и эти столбцы ортонормированны:
 .
.
Тогда для матрицы ковариации ![]() получим:
получим:
![]() =
=![]() =
=
![]()
На основании выражения (9) и с учетом (4) получим:
![]() . (10)
. (10)
Можно сделать вывод о том, что ортогональное преобразование пространства признаков не меняет энтропии (3) для вектора ![]() . Из свойств ортогонального преобразования вытекает, что оно не изменяет расстояний в пространстве признаков и эквивалентно повороту относительно центра рассеивания. Рассеивание, в нашем случае, описывается матрицей ковариации вектора признаков
. Из свойств ортогонального преобразования вытекает, что оно не изменяет расстояний в пространстве признаков и эквивалентно повороту относительно центра рассеивания. Рассеивание, в нашем случае, описывается матрицей ковариации вектора признаков ![]() . Для многомерного гауссового распределения
. Для многомерного гауссового распределения ![]() из (2а) видно, что поверхность постоянной плотности вероятности вектора признаков
из (2а) видно, что поверхность постоянной плотности вероятности вектора признаков ![]() является поверхность второго порядка. Учитывая симметричный характер гауссового распределения относительно вектора математического ожидания
является поверхность второго порядка. Учитывая симметричный характер гауссового распределения относительно вектора математического ожидания ![]() , установлено, что эта поверхность - L-мерный эллипсоид рассеивания [7]. Поскольку в результате выполнения ортогонального преобразования матрица ковариации вектора признаков
, установлено, что эта поверхность - L-мерный эллипсоид рассеивания [7]. Поскольку в результате выполнения ортогонального преобразования матрица ковариации вектора признаков ![]() приведена к диагональному виду (4), то это означает, что полуоси эллипсоида указывают направления максимального рассеивания в L-мерном пространстве признаков. Смысл ортогонального преобразования
приведена к диагональному виду (4), то это означает, что полуоси эллипсоида указывают направления максимального рассеивания в L-мерном пространстве признаков. Смысл ортогонального преобразования ![]() заключается в повороте системы координат относительно центра рассеивания
заключается в повороте системы координат относительно центра рассеивания ![]() до совмещения координатных осей
до совмещения координатных осей ![]() с главными полуосями рассеивания в L-мерном пространстве признаков. Так как каждый
с главными полуосями рассеивания в L-мерном пространстве признаков. Так как каждый ![]() -й класс образов имеет свой эллипсоид рассеивания, то задача выбора набора признаков, обеспечивающих решение задачи распознавания с максимальным уровнем вероятности распознавания
-й класс образов имеет свой эллипсоид рассеивания, то задача выбора набора признаков, обеспечивающих решение задачи распознавания с максимальным уровнем вероятности распознавания ![]() сводится к рассмотрению геометрической задаче с K эллипсоидами постоянной плотности вероятности.
сводится к рассмотрению геометрической задаче с K эллипсоидами постоянной плотности вероятности.
Геометрический подход к задаче разделимости классов
Для определенности будем рассматривать эллипсоиды постоянной плотности вероятности с полуосями равными ![]() , где
, где![]() - собственные значения выборочной ковариационной матрицы (4). Заметим, что эту цифру (3) далее в статье мы уточним! Тогда при условии независимости компонент вектора признаков
- собственные значения выборочной ковариационной матрицы (4). Заметим, что эту цифру (3) далее в статье мы уточним! Тогда при условии независимости компонент вектора признаков ![]() (соответствует диагональному виду
(соответствует диагональному виду ![]() ), на основании правила «3-х СКО» для гауссового закона распределения 99,7% всех реализаций вектора признаков для соответствующего класса образов будет находиться внутри эллипсоида рассеивания. При этом правильность выбора вектора признаков
), на основании правила «3-х СКО» для гауссового закона распределения 99,7% всех реализаций вектора признаков для соответствующего класса образов будет находиться внутри эллипсоида рассеивания. При этом правильность выбора вектора признаков ![]() будет интерпретироваться как отсутствие пересечений эллипсоидов рассеивания различных классов.
будет интерпретироваться как отсутствие пересечений эллипсоидов рассеивания различных классов.
На основании приведенных выше рассуждений сформулируем третий принцип: описание каждого класса в L-мерном пространстве признаков определяется его эллипсоидом рассеивания с центром ![]() и полуосями равными
и полуосями равными ![]() , где
, где![]() - собственные значения выборочной ковариационной матрицы вектора признаков по обучающей выборке класса.
- собственные значения выборочной ковариационной матрицы вектора признаков по обучающей выборке класса.
В работе [8] приведена теорема.
Теорема 1. Пусть ![]() и
и ![]() – квадрики в RL, причем первая является эллипсоидом. Квадрики не пересекаются тогда и только тогда, когда матрица
– квадрики в RL, причем первая является эллипсоидом. Квадрики не пересекаются тогда и только тогда, когда матрица ![]() является знакоопределенной.
является знакоопределенной.
Данная теорема может быть использована для матриц ![]() и
и ![]() . Применяя критерий Сильвестра[9] для матрицы
. Применяя критерий Сильвестра[9] для матрицы ![]() , необходимо проверить, что все главные миноры матрицы
, необходимо проверить, что все главные миноры матрицы ![]() положительны, либо все главные миноры отрицательны.
положительны, либо все главные миноры отрицательны.
Непересечение эллипсоидов рассеивания различных классов является необходимым условием при выборе эффективного набора признаков классификатора образов. В случае зашумления вектора признаков среднеквадратические отклонения ошибок (СКО) компонент вектора признаков, а, следовательно, и главные оси эллипсоидов рассевания будут расти, что, в конце концов, приведет к их пересечению и возникновению состояния неопределенности. Для контроля выполнения необходимого критерия выбора признаков и оценки устойчивости классификатора к шумам можно использовать расстояние между близкими классами (эллипсоидами рассеивания). Для этого воспользуемся следующей теоремой [8].
Теорема 2. Если выполняется условие теоремы 1, то квадрат расстояния между эллипсоидом ![]() и квадрикой
и квадрикой ![]() совпадает с минимальным положительным корнем полинома
совпадает с минимальным положительным корнем полинома
![]()
в предположении, что этот корень не является кратным. Здесь ![]() — дискриминант полинома, рассматриваемого относительно переменной
— дискриминант полинома, рассматриваемого относительно переменной ![]() .
.
Таким образом, для каждой пары близких эллипсоидов рассеивания с матрицами ![]() и
и ![]() необходимо составить матрицу размерности L×L:
необходимо составить матрицу размерности L×L: ![]() . Далее, разложив детерминант
. Далее, разложив детерминант ![]() в виде характеристического многочлена по степеням
в виде характеристического многочлена по степеням ![]() , получим полином порядка n = L+2:
, получим полином порядка n = L+2: ![]() , где
, где ![]() . Отметим, что дискриминант полинома равен нулю тогда и только тогда, когда полином имеет кратные корни. Поскольку машинное определение выборочной оценки ковариационных матриц выполняется с точностью до погрешностей округления, то событие получения кратных корней практически является маловероятным. Выражение для дискриминанта имеет вид:
. Отметим, что дискриминант полинома равен нулю тогда и только тогда, когда полином имеет кратные корни. Поскольку машинное определение выборочной оценки ковариационных матриц выполняется с точностью до погрешностей округления, то событие получения кратных корней практически является маловероятным. Выражение для дискриминанта имеет вид:
![]()
где ![]() - результант полинома
- результант полинома ![]() и его производной
и его производной ![]()
![]() .
.
Результант![]() равен определителю следующей (2n-1)×(2n-1) матрицы:
равен определителю следующей (2n-1)×(2n-1) матрицы:
dn | dn-1 | dn-2 | . | . | . | d0 | 0 | . | . | 0 |
0 | dn | dn-1 | dn-2 | . | . | . | d0 | 0 | . | 0 |
. | . | . | . | . | . | . | . | . | . | . |
0 | 0 | 0 | 0 | 0 | dn | dn-1 | dn-2 | . | . | d0 |
ndn | (n-1)dn-1 | (n-2)dn-2 | . | . | d1 | 0 | 0 | . | . | 0 |
0 | ndn | (n-1)dn-1 | (n-2)dn-2 | . | . | d1 | 0 | 0 | . | 0 |
0 | 0 | ndn | (n-1)dn-1 | (n-2)dn-2 | . | . | d1 | 0 | . | 0 |
. | . | . | . | . | . | . | . | . | . | . |
0 | 0 | 0 | 0 | 0 | 0 | ndn-1 | (n-1)dn-2 | (n-2)dn-2 | . | d1 |
Тогда, выбирая минимальный положительный корень - ![]() полинома
полинома ![]() , получим евклидово расстояние между двумя эллипсоидами в L-мерном пространстве признаков:
, получим евклидово расстояние между двумя эллипсоидами в L-мерном пространстве признаков:
![]() .
.
Отметим, что указанная процедура оценки расстояний может быть рассчитана на этапе проектирования классификатора. Выполняя пропорциональное расширение (k-коэффициент пропорциональности) главных полуосей эллипсоида рассеивания
![]()
получим таблицу соответствий ![]() расстояний между классами jи s. Максимальное значение k при котором
расстояний между классами jи s. Максимальное значение k при котором ![]() , определит запас устойчивости выбранного набора Lпризнаков к воздействию шума.
, определит запас устойчивости выбранного набора Lпризнаков к воздействию шума.
На основании утверждений теоремы 1 и 2 сформулируем четвертый принцип: расстояния ![]() между классами jи sдля обучающих выборок этих классов определяет запас устойчивости
между классами jи sдля обучающих выборок этих классов определяет запас устойчивости  выбранной пары классов к воздействию шума.
выбранной пары классов к воздействию шума.
При некотором упрощении задачи может быть получена оценка вероятности распознавания. Выполняя процедуру нормализации и ранжирования (7а) собственных значений для выборочной ковариационной матрицы каждого класса, можно оставить только три значимых компоненты вектора признака:
![]() .
.
В работе [7] найдено аналитическое выражение для вероятности попадания случайного трехмерного вектора признаков с гауссовой плотностью вероятности в эллипсоид рассеивания:
 .
.
Здесь, как и при составлении таблицы расстояний между классами, полуоси эллипсоида (a,b,с) пропорциональны СКО компонент вектора признаков:
![]() (11)
(11)
В соответствии с выражением (2а) при L=3, выполняя замену
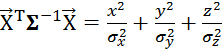 ,
,
получим выражение для вероятности попадания вектора признаков ![]() =(x,y,z)Tв эллипсоид Bk:
=(x,y,z)Tв эллипсоид Bk:
 .
.
Переходя к сферическим координатам и интегрируя по частям, получим:
 (12)
(12)
где  - функция Лапласа[7].
- функция Лапласа[7].
В [5] показано, что уровень значимости признаков, как правило, резко падает с увеличением ранжированного номера собственного значения выборочной матрицы ковариации и на основании (7) относительная ошибка представления вектора признаков для размерности L>3 составит единицы процента. Реализация вектора признаков ![]() =(x,y,z)Tпозволяет выразить отклонение от центра эллипсоида рассеивания
=(x,y,z)Tпозволяет выразить отклонение от центра эллипсоида рассеивания ![]() через расстояние, выраженное в среднеквадратических отклонениях, аналогично (11):
через расстояние, выраженное в среднеквадратических отклонениях, аналогично (11):
![]()
Значения СКО здесь получены на этапе первичного обучения, поэтому для вектора признака ![]() =(x,y,z)T могут быть найдены такие значения
=(x,y,z)T могут быть найдены такие значения ![]() , которые для заданного класса
, которые для заданного класса ![]() (с вектором
(с вектором ![]() матрицей
матрицей ![]() ) определяют расстояние до центра эллипсоида, выраженное в СКО. Подставляя
) определяют расстояние до центра эллипсоида, выраженное в СКО. Подставляя ![]() в (12), получим вероятность попадания в эллипсоид
в (12), получим вероятность попадания в эллипсоид ![]() . На рисунке 2 представлены 3 зависимости вероятности попадания
. На рисунке 2 представлены 3 зависимости вероятности попадания![]() , при этом
, при этом ![]() представляет собой двухмерный эллипс, трехмерный эллипсоид и трехмерный куб. Для трехмерного эллипсоида при
представляет собой двухмерный эллипс, трехмерный эллипсоид и трехмерный куб. Для трехмерного эллипсоида при ![]() в соответствии с (12) вычислено k=3.9, что превышает оценку для трехмерного куба k=3.4 (обобщенное «правило трех сигм» на пространство R3). Это факт свидетельствует о том, что не правомерно использовать аппроксимацию многомерного эллипсоида соответствующей размерности параллелепипедом, так как в этом случае получается завышенная оценка вероятности, а доверительные интервалы имеют заниженную оценку. Для эллипсоида рассеивания доверительный интервал составил ±3,9 СКО, что на 15 % больше, чем у куба.
в соответствии с (12) вычислено k=3.9, что превышает оценку для трехмерного куба k=3.4 (обобщенное «правило трех сигм» на пространство R3). Это факт свидетельствует о том, что не правомерно использовать аппроксимацию многомерного эллипсоида соответствующей размерности параллелепипедом, так как в этом случае получается завышенная оценка вероятности, а доверительные интервалы имеют заниженную оценку. Для эллипсоида рассеивания доверительный интервал составил ±3,9 СКО, что на 15 % больше, чем у куба.

Рисунок 2 – Зависимость ![]() от СКО, где
от СКО, где ![]() - эллипсоид, куб и эллипс
- эллипсоид, куб и эллипс
Cформулируем пятый принцип селекции информационных признаков образов: эллипсоиды рассеивания для всех K классов строятся на основе обучающих выборок этих классов, полуоси эллипсоидов определяются в соответствии с выражением (11), где k=3,9. При этом корректный набор признаков должен обеспечить высокий запас устойчивости:
![]()
Оценка вероятность распознавания образа каждого класса
Найдем теперь вероятность того, что реализация вектора признаков ![]() принадлежит классу
принадлежит классу ![]() из множества классов Ω = {𝜔j, j=1…K}. Эта вероятность является апостериорной, поскольку вычисляется на основе реализации вектора признаков
из множества классов Ω = {𝜔j, j=1…K}. Эта вероятность является апостериорной, поскольку вычисляется на основе реализации вектора признаков ![]() . Тогда в соответствии с формулой Байеса [5] получим:
. Тогда в соответствии с формулой Байеса [5] получим:
Вероятность того, что реализация вектора признаков ![]() принадлежит классу
принадлежит классу ![]() , определяется выражением:
, определяется выражением:
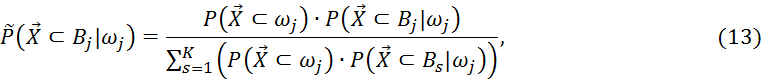
где ![]() - априорная вероятность принадлежности вектора
- априорная вероятность принадлежности вектора ![]() классу
классу ![]() ,
, ![]() -условная вероятность события
-условная вероятность события ![]() при условии, что произошло событие
при условии, что произошло событие ![]() . Если классификатор распознает 100 классов (К=100) и все события
. Если классификатор распознает 100 классов (К=100) и все события ![]() равновероятны, то
равновероятны, то ![]() и (13) упрощается:
и (13) упрощается:

Из постановки задачи следует, что совместная вероятность независимых событий определяется произведением их вероятностей. Тогда вероятность распознавания класса ![]() определяется принадлежностью
определяется принадлежностью ![]() к эллипсоиду
к эллипсоиду ![]() (
(![]() ) и непринадлежностью к другим эллипсоидам с вероятностью (
) и непринадлежностью к другим эллипсоидам с вероятностью (![]() ):
):

Подчеркнем тот факт, что выражение (15) позволяет оценивать максимальную вероятность распознавания объекта на множестве классов Ω, так как на этапе разработки (при обучении) системы учитываются СКО, обусловленные лишь ошибками квантования (оцифровки) сигнала изображения. В действительности СКО компонент вектора признаков всегда будет больше на реальном сигнале.
Таким образом, получена оценка вероятности распознавания для каждого класса ![]() . Найдем вероятность распознавания образа
. Найдем вероятность распознавания образа ![]() для заданного набора признаков
для заданного набора признаков ![]() , как минимальное значение вероятности
, как минимальное значение вероятности ![]() для всех Kклассов:
для всех Kклассов:
![]() (16)
(16)
В результате сформулированы ряд принципов и определен критерий выбора набора признаков по максимуму вероятности распознавания образов ![]() , обеспечивающих решение задачи распознавания с определенным уровнем вероятности распознавания (16). Это значение
, обеспечивающих решение задачи распознавания с определенным уровнем вероятности распознавания (16). Это значение ![]() соответствует минимальному искажению входного сигнала, так как учитывается только дискретная форма представления сигнала
соответствует минимальному искажению входного сигнала, так как учитывается только дискретная форма представления сигнала ![]() . При увеличении отношения сигнал/шум эллипсоид рассеивания расширяется (рост СКО). Последнее обстоятельство в соответствии с (12) приводит к увеличению k и снижению вероятностей
. При увеличении отношения сигнал/шум эллипсоид рассеивания расширяется (рост СКО). Последнее обстоятельство в соответствии с (12) приводит к увеличению k и снижению вероятностей ![]() . В случае аномального роста погрешностей признаков эллипсоиды рассеивания разных классов пересекаются и это еще более резко снижает
. В случае аномального роста погрешностей признаков эллипсоиды рассеивания разных классов пересекаются и это еще более резко снижает ![]() .
.
Существенная размерность пространства признаков классов
Сформулируем еще один принцип по выбору размерности набора признаков ![]() , обеспечивающих решение задачи распознавания с соответствующим ему максимальным уровнем вероятности распознавания.
, обеспечивающих решение задачи распознавания с соответствующим ему максимальным уровнем вероятности распознавания.
С одной стороны в соответствии с методом величина ![]() определяется максимальным рангом матриц ковариаций
определяется максимальным рангом матриц ковариаций ![]() то есть
то есть
![]()
Заметим, что выражение (17) скорее является верхней границей для выбора размерности пространства признаков. Как правило, назначая уровень значимости признаков, удается существенно понизить размерность этого пространства, например, используя упорядоченный набор собственных значений разложения Карунена-Лоева для ковариационной матрицы класса. Именно в этой связи был введен термин “существенная размерность” и на основании (15), (16) получим значение ![]() .
.
С другой стороны, минимальное возможное число признаков описывается степенями свободы физической системы. Например, движение твердого тела в пространстве описывается 6 фазовыми координатами (3- линейных , 3- угловых). Считая, что вдоль каждой фазовой координаты необходимо иметь хотя бы 1 координату вектора признаков, получим 6 компонент. Если движения объекта можно считать плоским, то получим 5 компонент (одно уравнение связи координат движения объекта, например y=0). Обобщая, приходим к выводу: если на движение объекта наложено mуравнений связи, то получим 6-mкомпонент вектора признаков. Тогда получим ![]() степеней свободы системы, значение
степеней свободы системы, значение ![]() определяет “истинную размерность” системы.
определяет “истинную размерность” системы.
Тогда для размерности пространства признаков можно записать:
![]() . (18)
. (18)
В этой связи может быть сформулирован принцип 6-существенной размерности пространства признаков: размерностью пространства признаков классификатора определяется выражением (18).
В заключении сформулируем выводы по работе.
1 Рассмотренные принципы построения классификаторов основываются на самых общих положениях статистической теории оценивания и теории информации и не используют конкретных методов и схем построения классификаторов.
2 Изложенные в статье принципы могут лечь в основу научно-обоснованного подхода к методике выбора наиболее информативных признаков классификаторов.
Работа поддержана Российским фондом фундаментальных исследований. Проект № 11-08-00292.
Список литературы
1. Hartley R.V.L. Transmission of Information // Bell System Technical Journal. July 1928. Vol. 7, no. 3. Р. 535-563.
2. Шеннон К. Работы по теории информации и кибернетике: пер. с англ. М.: Издательство иностранной литературы, 1963. 832 с.
3. Shore J.E., Johnson R.W. Axiomatic derivation of the principle of maximum entropy and the principle of minimum cross-entropy // IEEE Transactions on Information Theory. 1980. Vol. IT-26. Р. 26-37.
4. Jaynes E.T. On the rationale of maximum-entropy methods // Proceedings of the IEEE. 1982. Vol. 70. Р. 939-952.
5. Фукунага К. Введение в статистическую теорию распознавания образов : пер. с англ. М.: Наука, 1979. 366 с.
6. Хайкин С. Нейронные сети: полный курс: пер. с англ. 2-е изд. М.: Издательский дом "Вильямc", 2006. 1104 с.
7. Вентцель Е.С. Теория вероятностей : учебн. для вузов. 5-е изд., стер. М.: Высшая школа, 1998. 576 с.
8. Uteshev A.Yu., Yashina M.V. Distance computation from an ellipsoid to a linear or a Quadric Surface in Rn // Computer Algebra in Scientific Computing, Springer Berlin Heidelberg, 2007, pp. 392-401. (Lecture Notes in Computer Science, vol. 4770). DOI: 10.1007/978-3-540-75187-8_31
9. Гантмахер Ф.Р. Теория матриц. М.: Наука, 1966. 576 с.
Публикации с ключевыми словами: распознавание образов, теория информации, селекция признаков, системы технического зрения
Публикации со словами: распознавание образов, теория информации, селекция признаков, системы технического зрения
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



