научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#2 Февраль 2005
В.И. Левин, д-р техн. наук, проф., Пензенский технологический институт
Теория автоматов в задачах анализа сложных изображений
Излагается математический аппарат непрерывной логики в задаче анализа сложных изображений, эффективное решение которой может быть получено благодаря использованию автоматической модели.
♦ 1. В работе [1] изложен математический аппарат так называемой непрерывной логики (НЛ) и описаны простейшие случаи его применения, связанные с информатикой: геометрическое моделирование, принятие приближенных решений, оптимизация и др. Существует также много других задач из области информатики и информационных технологий, которые эффективно решаются с помощью аппарата НЛ или его обобщений [1]. В частности, когда объект исследования сложный (высокоразмерный), весьма эффективным оказывается применение аппарата логических определителей. Надо заметить, что при исследовании сложных объектов “наивное” моделирование простых объектов [1] в терминах НЛ не применимо и приходится искать специальные, достаточно мощные модели для получения адекватного непрерывно-логического описания объекта. Одной из наиболее результативных моделей такого рода является конечный динамический автомат [2-4].
В настоящей статье речь идет о проблеме анализа изображений, которая может быть эффективно решена именно благодаря использованию автоматной модели.
Суть этой проблемы состоит в том, чтобы по имеющемуся изображению в виде совокупности визуальных объектов в пространстве данной размерности формальным путем вычислить характеристики взаиморасположения объектов, по которым можно было бы анализировать указанное изображение для более полного понимания.
♦ 2. Рассмотрим произвольное N-мерное
евклидово пространство ЕN,
заполненное N-мерными объектами, с общим числом
объектов n. Объекты считаются “взаимопроникающими”
(пересекающимися), т.е. заполнение любым объектом любой области ![]() не препятствует
нахождению в
не препятствует
нахождению в ![]() другого
объекта. Положение каждого объекта в пространстве ЕN полностью определено. Очевидно, что изображение P, получающееся в результате взаимодействия всех
имеющихся объектов пространства ЕN,
можно представить в виде объединения изображений
другого
объекта. Положение каждого объекта в пространстве ЕN полностью определено. Очевидно, что изображение P, получающееся в результате взаимодействия всех
имеющихся объектов пространства ЕN,
можно представить в виде объединения изображений
![]() (1)
(1)
где ![]() - изображение
пересечений k различных объектов, включающее
изображения P(i1,
i2,… ik)
всех возможных конкретных комбинаций (i1,
i2,… ik)
k пересекающихся объектов, т.е.
- изображение
пересечений k различных объектов, включающее
изображения P(i1,
i2,… ik)
всех возможных конкретных комбинаций (i1,
i2,… ik)
k пересекающихся объектов, т.е.
 (2)
(2)
где P0 — псевдоизображение в некоторой области ![]() пространства EN, не содержащее ни одного объекта; P1 - изображение в другой области
пространства EN, не содержащее ни одного объекта; P1 - изображение в другой области ![]() пространства EN, в которой имеются только одиночные, не
пересекающиеся с другими объекты; P2
- изображение в третьей области
пространства EN, в которой имеются только одиночные, не
пересекающиеся с другими объекты; P2
- изображение в третьей области ![]() пространства ЕN, в которой имеются только попарно пересекающиеся
объекты, и т.д. и Рn -
изображение в области
пространства ЕN, в которой имеются только попарно пересекающиеся
объекты, и т.д. и Рn -
изображение в области ![]() пространства EN,
содержащей только пересечение всех n объектов.
пространства EN,
содержащей только пересечение всех n объектов.
Ясно, что
![]() (3)
(3)
В свою очередь,
![]() (4)
(4)
где ![]() - область пространства
EN, в которой имеется пересечение
только конкретного набора k объектов J=(i1,…, ik).
- область пространства
EN, в которой имеется пересечение
только конкретного набора k объектов J=(i1,…, ik).
Задача 1 состоит в том, чтобы найти области ![]() , соответствующие изображениям Рk в виде пересечений любого фиксированного числа k неконкретизированных объектов
, соответствующие изображениям Рk в виде пересечений любого фиксированного числа k неконкретизированных объектов ![]() . Задача 2 состоит в том, чтобы
найти области
. Задача 2 состоит в том, чтобы
найти области ![]() ,
соответствующие изображениям Pk(J) в виде пересечений J=(i1,…, ik)
любого числа к конкретных объектов
,
соответствующие изображениям Pk(J) в виде пересечений J=(i1,…, ik)
любого числа к конкретных объектов ![]() . Задача 2 является более детализированной,
из ее решения всегда можно получить решение задачи 1, используя формулу (4).
Задачи 1, 2 назовем задачами анализа изображения Р.
. Задача 2 является более детализированной,
из ее решения всегда можно получить решение задачи 1, используя формулу (4).
Задачи 1, 2 назовем задачами анализа изображения Р.
♦ 3. Сформулированные задачи для пространств EN различной размерности N можно интерпретировать следующим образом.
1) Пространство Е1, т.е. прямая. Для него объектами
являются заданные на прямой интервалы, причем допустимо пересечение интервалов
по 2, по 3 и т.д. вплоть до n (n - общее число интервалов). Требуется найти участки
прямой ![]() . на
которых пересекается ровно k любых интервалов,
. на
которых пересекается ровно k любых интервалов, ![]() (задача 1), либо найти
участки прямой
(задача 1), либо найти
участки прямой ![]() ,
на которых пересекается ровно k конкретных
интервалов
,
на которых пересекается ровно k конкретных
интервалов ![]() (задача
2).
(задача
2).
2) Пространство Е2, т.е. плоскость. Для него объектами
являются заданные на плоскости прямоугольники, стороны которых параллельны осям
координат, причем допустимо пересечение прямоугольников по 2, по 3,..., по n (n — общее число
прямоугольников). Выбор в качестве взаимодействующих объектов на плоскости
именно прямоугольников, очевидно, не ограничивает общности рассмотрения, так
как любую плоскую фигуру можно представить с любой степенью точности с помощью
вписанных в нее "плотно упакованных" прямоугольников. Требуется найти
области на плоскости ![]() ,
в которых пересекаются ровно k любых прямоугольников,
,
в которых пересекаются ровно k любых прямоугольников,
![]() (задача 1),
либо найти области на плоскости
(задача 1),
либо найти области на плоскости ![]() в которых пересекается k конкретных прямоугольников
в которых пересекается k конкретных прямоугольников ![]() (задача 2).
(задача 2).
3) Пространство Е3, т.е. трехмерное
пространство. Здесь объектами являются заданные в нем прямые параллелепипеды со
сторонами, параллельными осям координат. Допустимо пересечение параллелепипедов
по 2, по 3,..., по n (n
- общее число параллелепипедов). Выбор в качестве объектов в трехмерном
пространстве прямых параллелепипедов не ограничивает общности, поскольку любой
трехмерный объект можно представить с любой степенью точности посредством
вписанных в него "плотно упакованных" прямых параллелепипедов.
Требуется найти области ![]() в пространстве Е3, в
которых пересекается ровно k параллелепипедов,
безразлично каких,
в пространстве Е3, в
которых пересекается ровно k параллелепипедов,
безразлично каких, ![]() (задача
1), либо найти области
(задача
1), либо найти области ![]() в Е3, в которых
пересекается k конкретных
параллелепипедов
в Е3, в которых
пересекается k конкретных
параллелепипедов ![]() (задача
2).
(задача
2).
4) Пространства EN,
![]() , т.е.
четырехмерное и более высокоразмерные пространства. Для них задачи 1, 2
совершенно аналогичны задачам для пространств E1,
E2, E3
и имеют такой же содержательный смысл, но не имеют той же наглядной
геометрической интерпретации. При этом в качестве объектов берутся N-мерные прямые параллелепипеды со сторонами,
параллельными N осям координат.
, т.е.
четырехмерное и более высокоразмерные пространства. Для них задачи 1, 2
совершенно аналогичны задачам для пространств E1,
E2, E3
и имеют такой же содержательный смысл, но не имеют той же наглядной
геометрической интерпретации. При этом в качестве объектов берутся N-мерные прямые параллелепипеды со сторонами,
параллельными N осям координат.
♦ 4. Будем рассматривать общий случай задач 1, 2 анализа
изображения P в пространстве EN произвольной размерности N. Согласно
(1), произвольное изображение P складывается из
изображений пересечения ![]() ровно к любых различных объектов, причем
области
ровно к любых различных объектов, причем
области ![]() существования
пересечений Pk для различных k, согласно (3), не пересекаются. В соответствии с этим
введем систему двоичных функций
существования
пересечений Pk для различных k, согласно (3), не пересекаются. В соответствии с этим
введем систему двоичных функций ![]() , в пространстве EN:
, в пространстве EN:
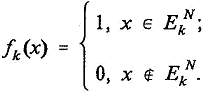 (5)
(5)
Как видно из (5), произвольная k-я функция
fk(x)
принимает значение 1 в области ![]() , где существует пересечение Pk, и значение 0 в других областях, где это
пересечение отсутствует. Поэтому функцию fk(x) естественно назвать k-й
обыкновенной спектральной функцией изображения P(1),
а совокупность всех таких функций f(x)={f0(x),…, fn(x)} - обыкновенным спектром указанного изображения.
Аналогично, согласно (2), произвольное пересечение Рk складывается из пересечений Pk(i1,…, ik)
ровно k различных, конкретно определенных
объектов i1,…, ik,
причем области
, где существует пересечение Pk, и значение 0 в других областях, где это
пересечение отсутствует. Поэтому функцию fk(x) естественно назвать k-й
обыкновенной спектральной функцией изображения P(1),
а совокупность всех таких функций f(x)={f0(x),…, fn(x)} - обыкновенным спектром указанного изображения.
Аналогично, согласно (2), произвольное пересечение Рk складывается из пересечений Pk(i1,…, ik)
ровно k различных, конкретно определенных
объектов i1,…, ik,
причем области ![]() существования
пересечений Pk(i1,…,
ik) для различных комбинаций объектов
(i1,..., ik),
согласно (4), не пересекаются. В соответствии с этим введем систему двоичных
функций
существования
пересечений Pk(i1,…,
ik) для различных комбинаций объектов
(i1,..., ik),
согласно (4), не пересекаются. В соответствии с этим введем систему двоичных
функций ![]() , в
пространстве EN, определяемых в виде
, в
пространстве EN, определяемых в виде
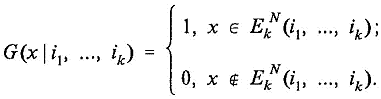 (6)
(6)
Из (6) видим, что произвольная k-я функция
![]() равна 1 в
области
равна 1 в
области ![]() , где
существует пересечение Pk(i1,..., ik),
и равна 0 в других областях, где это пересечение отсутствует. В соответствии с
этим данную функцию назовем k-й маркированной
спектральной функцией изображения Р [точнее, k-й
спектральной функцией, маркированной конкретной k-местной
комбинацией изображаемых объектов (i1,...,
ik)]. Совокупность всех таких функций
для всевозможных комбинаций объектов по 1, по 2,..., по n
назовем маркированным спектром изображения P и
обозначим G(x).
Таким образом, в отличие от обыкновенного спектра, отдельные спектральные
функции которого выделяют области пространства с изображением пересечения того
или иного числа объектов (безотносительно к составу пересекающихся объектов), в
маркированном спектре отдельные спектральные функции выделяют области
пространства, где изображено пересечение конкретных комбинаций объектов. Однако
и те и другие обладают свойством индикации областей со всеми возможными
типовыми фрагментами заданного изображения. Это подсказывает идею решения задач
1 и 2 анализа изображения, рассматриваемую в следующем пункте.
, где
существует пересечение Pk(i1,..., ik),
и равна 0 в других областях, где это пересечение отсутствует. В соответствии с
этим данную функцию назовем k-й маркированной
спектральной функцией изображения Р [точнее, k-й
спектральной функцией, маркированной конкретной k-местной
комбинацией изображаемых объектов (i1,...,
ik)]. Совокупность всех таких функций
для всевозможных комбинаций объектов по 1, по 2,..., по n
назовем маркированным спектром изображения P и
обозначим G(x).
Таким образом, в отличие от обыкновенного спектра, отдельные спектральные
функции которого выделяют области пространства с изображением пересечения того
или иного числа объектов (безотносительно к составу пересекающихся объектов), в
маркированном спектре отдельные спектральные функции выделяют области
пространства, где изображено пересечение конкретных комбинаций объектов. Однако
и те и другие обладают свойством индикации областей со всеми возможными
типовыми фрагментами заданного изображения. Это подсказывает идею решения задач
1 и 2 анализа изображения, рассматриваемую в следующем пункте.
♦ 5. Так как все объекты в пространстве EN
есть N-мерные прямые параллелепипеды в EN со сторонами, параллельными N осям
координат, то пересечение любого числа k
объектов ![]() также
является N-мерным прямым параллелепипедом в EN со сторонами, параллельными N осям
координат. Поэтому любое неконкретизированное Рk
либо конкретизированное Pk{i1,..., ik)
по составу пересечение k объектов можно спроектировать
на все оси координат х1,..., xN:
также
является N-мерным прямым параллелепипедом в EN со сторонами, параллельными N осям
координат. Поэтому любое неконкретизированное Рk
либо конкретизированное Pk{i1,..., ik)
по составу пересечение k объектов можно спроектировать
на все оси координат х1,..., xN:
![]() (7)
(7)
 (8)
(8)
где Pk(x) -
проекция пересечения объектов Рk
на ось xi, a ![]() —
проекция пересечения объектов Рk(i1,.., ik)
на ту же ось. Различие между этими проекциями то же, что и в исходных
пересечениях: в проекции Рk(хi) указывается только число k
объектов в исходном пересечении, а в проекции
—
проекция пересечения объектов Рk(i1,.., ik)
на ту же ось. Различие между этими проекциями то же, что и в исходных
пересечениях: в проекции Рk(хi) указывается только число k
объектов в исходном пересечении, а в проекции ![]() дается еще конкретный перечень (i1,..., ik)
объектов в пересечении. Любое пересечение Рk,
согласно (2), состоит в общем случае из
дается еще конкретный перечень (i1,..., ik)
объектов в пересечении. Любое пересечение Рk,
согласно (2), состоит в общем случае из ![]() разнесенных в пространстве пересечений Рk(i1,.., ik) конкретных объектов (i1,..,
ik),
разнесенных в пространстве пересечений Рk(i1,.., ik) конкретных объектов (i1,..,
ik), ![]() . Поэтому проекция пересечения Рk на любую ось также состоит в общем случае из
. Поэтому проекция пересечения Рk на любую ось также состоит в общем случае из ![]() разнесенных вдоль этой
оси проекций на нее пересечений Рk(i1,.., ik)
(которые тоже делимы):
разнесенных вдоль этой
оси проекций на нее пересечений Рk(i1,.., ik)
(которые тоже делимы):
![]()
В этом второе различие между проекциями (7) и (8). Сходство между ними в следующем: имеется однозначное соответствие любого пересечения объектов Рk(i1,.., ik) и его проекций и однозначное соответствие любого пересечения объектов Рk и его проекций при отсутствии в общем случае однозначного обратного соответствия. Однако в случае N=1 (т.е. в одномерном пространстве) имеется взаимооднозначное соответствие между пересечениями объектов и их проекциями на единственную в этом случае ось.
Введенные проекции пересечений N-мерных
объектов - обыкновенные Рk(хr) и маркированные ![]() - являются уже одномерными объектами, с
которыми значительно проще работать. Для них общие N-мерные
спектральные функции - обыкновенные (5) и маркированные (6) — переходят в
соответствующие спектральные функции от одной переменной:
- являются уже одномерными объектами, с
которыми значительно проще работать. Для них общие N-мерные
спектральные функции - обыкновенные (5) и маркированные (6) — переходят в
соответствующие спектральные функции от одной переменной:
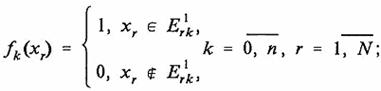 (9)
(9)
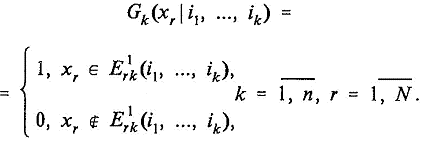 (10)
(10)
Согласно (9), k-я функция fk(хr)
принимает значение 1 в той части ![]() оси xr
где существует проекция Рk(хr) пересечения Рk,
и значение 0 в других частях, где эта проекция отсутствует. Поэтому функцию fk(хr)
можно назвать k-й обыкновенной одномерной
спектральной функцией проекции Рk(хr) пересечения Рk
на ось хr. Аналогично,
согласно (10), k-я функция
оси xr
где существует проекция Рk(хr) пересечения Рk,
и значение 0 в других частях, где эта проекция отсутствует. Поэтому функцию fk(хr)
можно назвать k-й обыкновенной одномерной
спектральной функцией проекции Рk(хr) пересечения Рk
на ось хr. Аналогично,
согласно (10), k-я функция ![]() равна 1 в той части
равна 1 в той части ![]() оси хr где существует проекция
оси хr где существует проекция ![]() пересечения Рk(i1,.., ik), и равна 0 в других частях, где эта
проекция отсутствует. Поэтому функцию
пересечения Рk(i1,.., ik), и равна 0 в других частях, где эта
проекция отсутствует. Поэтому функцию ![]() можно назвать k-й
маркированной одномерной спектральной функцией проекций
можно назвать k-й
маркированной одномерной спектральной функцией проекций ![]() пересечения Рk(i1,.., ik) на ось хr.
пересечения Рk(i1,.., ik) на ось хr.
Совокупность всех функций ![]() назовем обыкновенным одномерным
спектром изображения Р (1) вдоль оси хr N-мерного пространства
назовем обыкновенным одномерным
спектром изображения Р (1) вдоль оси хr N-мерного пространства ![]() . Аналогично
совокупность всех функций
. Аналогично
совокупность всех функций ![]() ,
, ![]() назовем маркированным одномерным спектром
изображения Р (1) вдоль оси хr N-мерного пространства
назовем маркированным одномерным спектром
изображения Р (1) вдоль оси хr N-мерного пространства ![]() .
.
Введенные одномерные спектры обладают свойством индикации участков соответствующих осей N-мерного пространства, на которых имеется проекция рассматриваемого пересечения объектов в этом пространстве. Отсюда следует, что задачи 1 и 2 анализа изображения в N-мерном пространстве целесообразно пытаться решить путем их сведения либо к анализу одномерных спектров проекций этого изображения на все N осей пространства, либо просто к вычислению одномерных спектров вдоль параллельных прямых, пересекающих изображение.
♦ 6. Реализацию идеи, высказанной в п. 5, начнем с задач
анализа изображений в одномерном пространстве, т.е. на прямой. Задача 1 в этом
случае состоит в следующем. На оси x задано
изображение P в виде совокупности n одномерных объектов - замкнутых интервалов ![]() (рис. 1).
(рис. 1).
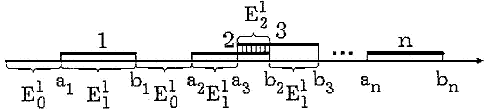
Рис. 1.
Эти интервалы
могут взаимодействовать между собой, образуя различные пересечения. В
результате изображение P распадается, согласно
(1), на изображения: P0 в области ![]() на оси x, не
на оси x, не
содержащее ни
одного интервала; Р1, в области ![]() содержащее только любые одиночные,
непересекающиеся с другими интервалы; Р2 в области
содержащее только любые одиночные,
непересекающиеся с другими интервалы; Р2 в области ![]() , содержащее только
попарно пересекающиеся интервалы, ..., Рn
в области
, содержащее только
попарно пересекающиеся интервалы, ..., Рn
в области ![]() ,
содержащей только пересечение всех n интервалов.
Задача заключается в нахождении областей
,
содержащей только пересечение всех n интервалов.
Задача заключается в нахождении областей ![]() , на оси x, содержащих изображения Рk,
, на оси x, содержащих изображения Рk, ![]() , в виде пересечения любого фиксированного
числа k неконкретизированных (т.е. любых)
интервалов.
, в виде пересечения любого фиксированного
числа k неконкретизированных (т.е. любых)
интервалов.
Будем
интерпретировать точки оси x как моменты времени.
Тогда задаче 1 с заданной системой интервалов можно поставить в соответствие
математическую модель в виде конечного автомата без памяти (рис. 2) с n двоичными входами ![]() , на которые подаются единичные импульсы 1(ai, bi)
(по одному на каждый вход), существующие во временных интервалах (ai, bi),
соответствующих заданным интервалам
, на которые подаются единичные импульсы 1(ai, bi)
(по одному на каждый вход), существующие во временных интервалах (ai, bi),
соответствующих заданным интервалам ![]() .
.

Рис. 2.
Этот автомат
имеет один двоичный выходу, ![]() , на котором реализуется фундаментальная
симметрическая булева функция
, на котором реализуется фундаментальная
симметрическая булева функция ![]() индекса
индекса ![]() n входных
переменных x1,…, xn.
Таким образом, выходная переменная автомата выражается через его входные
переменные в виде
n входных
переменных x1,…, xn.
Таким образом, выходная переменная автомата выражается через его входные
переменные в виде
![]()
Как известно [4], фундаментальная симметрическая булева функция ![]() =1 только тогда, когда p любых ее аргументов равны 1, и
=1 только тогда, когда p любых ее аргументов равны 1, и ![]() =0 в остальных случаях. Таким
образом, выходная переменная автомата-модели y=1
только тогда, когда p любых его входных
переменных x, равны 1. Это означает, что на
выходе этого автомата единичные импульсы вырабатываются в тех временных
интервалах, в которых на его входах действует одновременно (пересекается) p входных единичных импульсов. Таким образом [см.
определения (5), (9)], автомат-модель (см. рис. 2) с реализуемой булевой
функцией
=0 в остальных случаях. Таким
образом, выходная переменная автомата-модели y=1
только тогда, когда p любых его входных
переменных x, равны 1. Это означает, что на
выходе этого автомата единичные импульсы вырабатываются в тех временных
интервалах, в которых на его входах действует одновременно (пересекается) p входных единичных импульсов. Таким образом [см.
определения (5), (9)], автомат-модель (см. рис. 2) с реализуемой булевой
функцией ![]() вырабатывает
на выходе обыкновенную одномерную спектральную функцию fp(x) одной переменной x,
отмечающую своими единичными значениями те области оси x,
в которых пересекается p из
и заданных интервалов
вырабатывает
на выходе обыкновенную одномерную спектральную функцию fp(x) одной переменной x,
отмечающую своими единичными значениями те области оси x,
в которых пересекается p из
и заданных интервалов ![]() . Варьируя значение индекса p функции
. Варьируя значение индекса p функции ![]() автомата-модели от 0 до n, получим обыкновенный одномерный спектр f(x)={f0(x), f1(x),…, fn(x)}, составляющие которого есть функции, отмечающие
области оси x, в которых пересекается любое
возможное число
автомата-модели от 0 до n, получим обыкновенный одномерный спектр f(x)={f0(x), f1(x),…, fn(x)}, составляющие которого есть функции, отмечающие
области оси x, в которых пересекается любое
возможное число ![]() заданных
интервалов [ai, bi].
Это и есть решение задачи 1 анализа изображения в одномерном пространстве. В
соответствии с изложенным алгоритм решения этой задачи таков.
заданных
интервалов [ai, bi].
Это и есть решение задачи 1 анализа изображения в одномерном пространстве. В
соответствии с изложенным алгоритм решения этой задачи таков.
Шаг 1. Построение математической модели задачи 1 с заданной
системой интервалов ![]() виде
конечного автомата без памяти с двоичными входами x1,...,
xn и выходом y
и реализуемой на выходе фундаментальной симметрической булевой функцией входов
виде
конечного автомата без памяти с двоичными входами x1,...,
xn и выходом y
и реализуемой на выходе фундаментальной симметрической булевой функцией входов ![]() с переменным индексом
с переменным индексом ![]() с воздействиями на
входах i в виде единичных импульсов xi(t)=1[ai, bi],
действующих во временных интервалах (ai, bi), соответствующих интервалам, заданным по
условию задачи (см. рис. 2).
с воздействиями на
входах i в виде единичных импульсов xi(t)=1[ai, bi],
действующих во временных интервалах (ai, bi), соответствующих интервалам, заданным по
условию задачи (см. рис. 2).
Шаг 2. Вычисление динамических процессов ![]() на выходе построенного
автомата-модели, соответствующих всем возможным значениям индекса p реализуемой автоматом функции
на выходе построенного
автомата-модели, соответствующих всем возможным значениям индекса p реализуемой автоматом функции ![]() . Это вычисление
ведется по следующей формуле теории динамических автоматов [4]:
. Это вычисление
ведется по следующей формуле теории динамических автоматов [4]:
 (11)
(11)
где ![]() - булево отрицание
дизъюнкции, а
- булево отрицание
дизъюнкции, а ![]() -
конъюнкция и дизъюнкция НЛ, т.е. операции min и max [1]. Здесь А' и В' - следующие логические
определители ранга r, составленные
соответственно из моментов аi,
изменений сигналов 0 → 1 и моментов bi
изменений сигналов 1 → 0 во входных воздействиях автомата-модели:
-
конъюнкция и дизъюнкция НЛ, т.е. операции min и max [1]. Здесь А' и В' - следующие логические
определители ранга r, составленные
соответственно из моментов аi,
изменений сигналов 0 → 1 и моментов bi
изменений сигналов 1 → 0 во входных воздействиях автомата-модели:

раскрываемые по формуле (34) [1]. В формуле (11) 1 (А, В) означают единичные импульсы в интервалах (А, В), а 0 (-,-) - нулевые паузы в промежуточных интервалах.
Шаг3. Интерпретация динамических процессов ![]() , на выходе автомата-модели как
обыкновенных спектральных функций
, на выходе автомата-модели как
обыкновенных спектральных функций ![]() с соответствующими
значениями индекса p. Каждая функция fp(x) есть
функция одной переменной x, отмечающая своими единичными
значениями те области
с соответствующими
значениями индекса p. Каждая функция fp(x) есть
функция одной переменной x, отмечающая своими единичными
значениями те области ![]() , оси x,
где пересекается p из n
заданных интервалов
, оси x,
где пересекается p из n
заданных интервалов ![]() .
Таким образом, получаем решение задачи 1 в виде
.
Таким образом, получаем решение задачи 1 в виде
 (12)
(12)
♦ 7. Перейдем к задаче 2 анализа изображения в одномерном
пространстве. Ее формулировка такова. На оси x
задано то же изображение Р в виде системы n интервалов ![]() , что и в задаче 1 (см. рис. 1).
Изображение Р, согласно п. 6, распадается на изображения Рk с
ровно k пересекающимися интервалами (любыми),
, что и в задаче 1 (см. рис. 1).
Изображение Р, согласно п. 6, распадается на изображения Рk с
ровно k пересекающимися интервалами (любыми), ![]() . В свою очередь, Рk, согласно (2), распадаются на изображения Pk(i1,…,
ik) возможных конкретных комбинаций (i1,…, ik)
k пересекающихся интервалов
. В свою очередь, Рk, согласно (2), распадаются на изображения Pk(i1,…,
ik) возможных конкретных комбинаций (i1,…, ik)
k пересекающихся интервалов
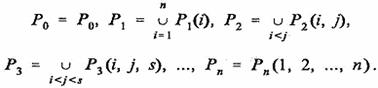 (13)
(13)
Задача состоит в нахождении областей ![]() ,
, ![]() на оси x,
содержащих изображения,
на оси x,
содержащих изображения,
![]() в виде пересечения k конкретных интервалов (i1,…,
ik). Как и при решении задачи 1 (см.
п. 6), интерпретируем ось x как временную ось, а
заданную систему интервалов — как систему единичных импульсов 1(ai, bi)
в соответствующих временных интервалах. Тогда задаче 2 с заданной системой
интервалов можно поставить в соответствие математическую модель в виде
конечного автомата без памяти (рис. 3), имеющего ту же структуру, что и
автомат-модель для задачи 1 (см. рис. 2): n
двоичных входов
в виде пересечения k конкретных интервалов (i1,…,
ik). Как и при решении задачи 1 (см.
п. 6), интерпретируем ось x как временную ось, а
заданную систему интервалов — как систему единичных импульсов 1(ai, bi)
в соответствующих временных интервалах. Тогда задаче 2 с заданной системой
интервалов можно поставить в соответствие математическую модель в виде
конечного автомата без памяти (рис. 3), имеющего ту же структуру, что и
автомат-модель для задачи 1 (см. рис. 2): n
двоичных входов ![]() на
которые подаются указанные единичные импульсы 1(ai,
bi) (по одному на каждый вход), и
один двоичный выход y,
на
которые подаются указанные единичные импульсы 1(ai,
bi) (по одному на каждый вход), и
один двоичный выход y, ![]() , но другую реализуемую на
выходе функцию входов
, но другую реализуемую на
выходе функцию входов
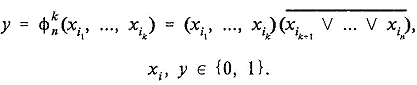 (14)
(14)

Рис. 3.
Первая скобка в формуле (14) есть булева конъюнкция, вторая — отрицание
булевой дизъюнкции. Функция ![]() равна 1 только тогда, когда
равна 1 только тогда, когда ![]() и равна 0 в остальных
случаях. Таким образом, выходная переменная автомата-модели y = 1 только тогда, когда ровно k
его конкретных входных переменных
и равна 0 в остальных
случаях. Таким образом, выходная переменная автомата-модели y = 1 только тогда, когда ровно k
его конкретных входных переменных ![]() равны 1.Это означает, что на выходе
данного автомата единичные импульсы вырабатываются только в тех временных
интервалах, в которых на его входах действуют одновременно (пересекаются) k конкретных входных единичных импульсов
равны 1.Это означает, что на выходе
данного автомата единичные импульсы вырабатываются только в тех временных
интервалах, в которых на его входах действуют одновременно (пересекаются) k конкретных входных единичных импульсов ![]()
![]() . Таким образом, в соответствии
с определениями (6), (10) автомат-модель, представленный на рис. 3, с
реализуемой булевой функцией
. Таким образом, в соответствии
с определениями (6), (10) автомат-модель, представленный на рис. 3, с
реализуемой булевой функцией ![]() вырабатывает на выходе одномерную
маркированную спектральную функцию
вырабатывает на выходе одномерную
маркированную спектральную функцию ![]() одной переменной x,
отмечающую своими единичными значениями ту область оси x,
в которой пересекается к конкретных интервалов
одной переменной x,
отмечающую своими единичными значениями ту область оси x,
в которой пересекается к конкретных интервалов ![]() из n
заданных интервалов
из n
заданных интервалов ![]() .
.
Варьируя
конкретный состав ![]() переменных
функции
переменных
функции ![]() автомата-модели
и их число
автомата-модели
и их число ![]() ,
получим одномерный маркированный спектр
,
получим одномерный маркированный спектр ![]() , составляющие которого — это функции,
отмечающие области оси x, в которых пересекается
конкретный по составу и числу набор из заданных интервалов [ai, bi].
Это и есть решение задачи 2 анализа изображения в одномерном пространстве.
Алгоритм решения этой задачи, согласно изложенному, следующий.
, составляющие которого — это функции,
отмечающие области оси x, в которых пересекается
конкретный по составу и числу набор из заданных интервалов [ai, bi].
Это и есть решение задачи 2 анализа изображения в одномерном пространстве.
Алгоритм решения этой задачи, согласно изложенному, следующий.
Шаг 1. Построение математической модели задачи 2 с заданной
системой интервалов ![]() , в виде конечного автомата без
памяти с двоичными входами x1,…, xn и выходом y
и реализуемой на выходе булевой функцией
, в виде конечного автомата без
памяти с двоичными входами x1,…, xn и выходом y
и реализуемой на выходе булевой функцией ![]() вида (14), с воздействием на входах i в виде единичных импульсов xi(t)=1(ai, bi), действующих во временных интервалах (ai, bi)
соответствующих интервалам, заданным по условию задачи (рис. 3). С учетом
явного выражения (14) реализуемой в автомате-модели булевой функции блок-схема
этого автомата (см. рис. 3) может быть конкретизирована и представлена как
структурная схема, показанная на рис. 4.
вида (14), с воздействием на входах i в виде единичных импульсов xi(t)=1(ai, bi), действующих во временных интервалах (ai, bi)
соответствующих интервалам, заданным по условию задачи (рис. 3). С учетом
явного выражения (14) реализуемой в автомате-модели булевой функции блок-схема
этого автомата (см. рис. 3) может быть конкретизирована и представлена как
структурная схема, показанная на рис. 4.
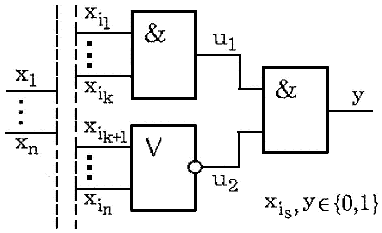
Рис. 4.
Шаг 2. Вычисление динамических процессов ![]() на выходе построенного автомата-модели,
соответствующих всем возможным значениям индекса k реализуемой автоматом функции
на выходе построенного автомата-модели,
соответствующих всем возможным значениям индекса k реализуемой автоматом функции ![]() ,
, ![]() , и всем возможным наборам входных
переменных
, и всем возможным наборам входных
переменных ![]() по
k. Это вычисление ведется по формулам теории
динамических автоматов с использованием метода последовательных подстановок
[4]:
по
k. Это вычисление ведется по формулам теории
динамических автоматов с использованием метода последовательных подстановок
[4]:
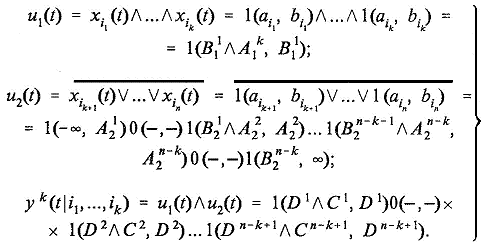
Здесь ![]() — логические
определители (ЛО) ранга r, составленные из
моментов ai, изменений сигнала 0 →
1 и моментов bi изменений
сигнала 1 → 0, во входных воздействиях автомата модели:
— логические
определители (ЛО) ранга r, составленные из
моментов ai, изменений сигнала 0 →
1 и моментов bi изменений
сигнала 1 → 0, во входных воздействиях автомата модели:
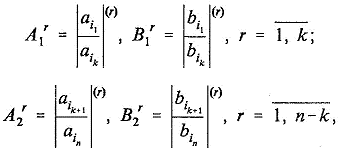 (15)
(15)
раскрываемые
по формуле (34) [1], а ![]() — сложные ЛО (т.е. ЛО от ЛО) ранга r.
— сложные ЛО (т.е. ЛО от ЛО) ранга r.
 (16)
(16)
раскрываемые по той же формуле.
Шаг З. Интерпретация процессов ![]() , на выходе автомата-модели как
маркированных спектральных функций
, на выходе автомата-модели как
маркированных спектральных функций ![]() , с соответствующими значениями индекса k и наборами переменных
, с соответствующими значениями индекса k и наборами переменных ![]() по k.
Каждая функция
по k.
Каждая функция ![]() есть
функция одной переменной x, отмечающая своими
единичными значениями те области
есть
функция одной переменной x, отмечающая своими
единичными значениями те области ![]() оси x, где
пересекается ровно k конкретных интервалов из n заданных интервалов
оси x, где
пересекается ровно k конкретных интервалов из n заданных интервалов ![]() , а именно
, а именно ![]() . Таким образом, при решении задачи 2 для ЛО
. Таким образом, при решении задачи 2 для ЛО
![]() в
соответствии с (16), вычисляемых по формуле (34) [1] и при конкретизации ЛО,
согласно (15), получим: при k=1
в
соответствии с (16), вычисляемых по формуле (34) [1] и при конкретизации ЛО,
согласно (15), получим: при k=1
![]()

При k=2
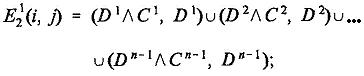

при k=3


……………………………………………………..
при заданном k
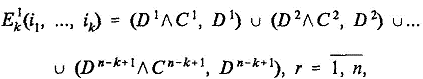

♦ 8. Теперь рассмотрим задачи анализа изображений в двумерном пространстве, т.е. на плоскости. Задачи 1, 2 в этом случае формулируются следующим образом. На плоскости в декартовой системе координат (x, y) задано изображение Р в виде совокупности n плоских объектов — прямоугольников со сторонами, параллельными осям координата x, y (рис. 5). Каждый i-й прямоугольник задается четырьмя параметрами (ai, bi, ci, di), где [ai, bi] — интервал, являющийся проекцией прямоугольника на ось x; [ci, di] — интервал, являющийся его проекцией на ось y. Прямоугольники, в соответствии с их заданными границами, могут взаимодействовать друг с другом, образуя различные пересечения.

Рис. 5.
В итоге изображение Р, согласно (1), распадается на изображения: P0 области ![]() на плоскости, не содержащее ни одного
прямоугольника; Р1, в области
на плоскости, не содержащее ни одного
прямоугольника; Р1, в области ![]() , содержащее только одиночные, не
пересекающиеся с другими прямоугольники (любые); Р2 в области
, содержащее только одиночные, не
пересекающиеся с другими прямоугольники (любые); Р2 в области
![]() , содержащее
только попарно пересекающиеся прямоугольники (любые); ... Рn в области
, содержащее
только попарно пересекающиеся прямоугольники (любые); ... Рn в области ![]() , содержащее только пересечение всех n прямоугольников. Задача 1 состоит в нахождении областей
, содержащее только пересечение всех n прямоугольников. Задача 1 состоит в нахождении областей
![]() , и, на
плоскости, содержащих изображения
, и, на
плоскости, содержащих изображения ![]() , в виде пересечения любого фиксированного
числа k неконкретизированных (т.е. любых)
прямоугольников. Изображения Рk
можно разбить в соответствии с (13) на изображения Pk(ii,..., ik)
возможных конкретных комбинаций (ii,...,
ik) к пересекающихся прямоугольников.
Тогда задача 2 сводится к нахождению областей
, в виде пересечения любого фиксированного
числа k неконкретизированных (т.е. любых)
прямоугольников. Изображения Рk
можно разбить в соответствии с (13) на изображения Pk(ii,..., ik)
возможных конкретных комбинаций (ii,...,
ik) к пересекающихся прямоугольников.
Тогда задача 2 сводится к нахождению областей ![]() , и, на плоскости, содержащей изображения
, и, на плоскости, содержащей изображения ![]() , в виде пересечения k конкретных прямоугольников ii,...,
ik.
, в виде пересечения k конкретных прямоугольников ii,...,
ik.
Для решения обеих задач применим метод сечений. Проведем некоторое число
сечений изображения (см. рис. 5) прямыми, параллельными одной из осей, например
оси х. Каждое такое сечение j вдоль
соответствующей прямой xj содержит
полную информацию о характере изображения вдоль этой прямой, конкретно о
прямоугольниках ![]() (и
их взаимодействии между собой), которые пересекаются с этой прямой, и о пустых
областях между прямоугольниками. Эта информация представляется совокупностью
всех интервалов [ai, bi] — проекций на ось x
всех пересекаемых прямой xj
прямоугольников i. Например, на рис. 5 сечение у
пересекает прямоугольники 1 и 2, которые не взаимодействуют между собой (не
пересекаются), поэтому вся информация об этих прямоугольниках, содержащаяся в
данном сечении, — это пара непересекающихся интервалов на оси x: интервал [a1,
b1] — проекция на ось x прямоугольника 1 и интервал [a2,
b2] — проекция на ось x прямоугольника 2. Аналогично сечение j - 1 пересекает прямоугольники
1, 2, 3, причем 2 и 3 взаимодействуют (пересекаются); вся информация об этих
прямоугольниках в данном сечении — три интервала на оси x:
изолированный [a1, b1] — проекция прямоугольника 1 и пара
пересекающихся [a2, b2] и [a3,
b3] - проекции пересекающихся
прямоугольников 2, 3. Далее, сечение j+2 не
пересекается ни с одним прямоугольником и поэтому содержит информацию только о
пустых областях, не заполненных прямоугольниками, и т.д.
(и
их взаимодействии между собой), которые пересекаются с этой прямой, и о пустых
областях между прямоугольниками. Эта информация представляется совокупностью
всех интервалов [ai, bi] — проекций на ось x
всех пересекаемых прямой xj
прямоугольников i. Например, на рис. 5 сечение у
пересекает прямоугольники 1 и 2, которые не взаимодействуют между собой (не
пересекаются), поэтому вся информация об этих прямоугольниках, содержащаяся в
данном сечении, — это пара непересекающихся интервалов на оси x: интервал [a1,
b1] — проекция на ось x прямоугольника 1 и интервал [a2,
b2] — проекция на ось x прямоугольника 2. Аналогично сечение j - 1 пересекает прямоугольники
1, 2, 3, причем 2 и 3 взаимодействуют (пересекаются); вся информация об этих
прямоугольниках в данном сечении — три интервала на оси x:
изолированный [a1, b1] — проекция прямоугольника 1 и пара
пересекающихся [a2, b2] и [a3,
b3] - проекции пересекающихся
прямоугольников 2, 3. Далее, сечение j+2 не
пересекается ни с одним прямоугольником и поэтому содержит информацию только о
пустых областях, не заполненных прямоугольниками, и т.д.
Выделим некоторое сечение j плоского изображения, проведенное вдоль прямой xj (см. рис. 5). Так как это сечение есть одномерное изображение, его анализ можно выполнить методами, изложенными в пп. 6, 7. В результате получим обыкновенный одномерный спектр плоского изображения Р вдоль секущей прямой xj.
![]()
где fk(xj)
— k-я обыкновенная спектральная функция
изображения Р вдоль прямой хj
принимающая значение 1 в той области ![]() прямой xj,
где есть проекция пересечения Рk
ровно k прямоугольников (любых) и 0 в других областях.
Аналогично получим маркированный одномерный спектр плоского изображения Р
вдоль секущей прямой xj
прямой xj,
где есть проекция пересечения Рk
ровно k прямоугольников (любых) и 0 в других областях.
Аналогично получим маркированный одномерный спектр плоского изображения Р
вдоль секущей прямой xj

где ![]() - k-я
маркированная одномерная спектральная функция изображения Р вдоль прямой
xj, принимающая значение 1 в той
области
- k-я
маркированная одномерная спектральная функция изображения Р вдоль прямой
xj, принимающая значение 1 в той
области ![]() прямой
xj, где есть проекция пересечения Pk(ii,...,
ik) ровно k
конкретных прямоугольников (i1-го,...,
ik-го) и значение 0 в других
областях. Объединив одномерные спектры вдоль всех секущих прямых хj получим соответствующие полные двумерные спектры:
прямой
xj, где есть проекция пересечения Pk(ii,...,
ik) ровно k
конкретных прямоугольников (i1-го,...,
ik-го) и значение 0 в других
областях. Объединив одномерные спектры вдоль всех секущих прямых хj получим соответствующие полные двумерные спектры:
![]() (17)
(17)
![]() (18)
(18)
Вычислив по формуле (17) обыкновенный спектр f(x, y) плоского изображения Р, найдем тем самым решение задачи 1. Аналогично, вычислив по формуле (18) маркированный спектр G(x, у) изображения Р, найдем решение задачи 2. Заметим, что в общем случае формулы (17), (18) и получаемые по ним решения задач 1, 2 являются приближенными, так как при большом расстоянии между секущими прямыми xj, часть информации о двумерных изображениях при объединении их одномерных составляющих теряется. Чтобы этого не произошло и решение было точным, достаточно провести по одной секущей на каждом участке, на котором изображение неизменно. Такие участки расположены между соседними точками появления новых или исчезновения старых прямоугольников, т.е. точками с ординатами
![]()
где ![]() — упорядоченные по
возрастанию ординаты с1..., сn,
d1,,..., dn
горизонтальных границ всех n прямоугольников
изображения.
— упорядоченные по
возрастанию ординаты с1..., сn,
d1,,..., dn
горизонтальных границ всех n прямоугольников
изображения.
Отсюда следует, что для получения точного решения задач 1 и 2 достаточно провести не более М=2n+1 секущих прямых.
♦ 9. Задачи 1 и 2 анализа изображения в трехмерном пространстве формулируются и решаются аналогично соответствующим плоским задачам. При этом за объекты в трехмерном изображении принимают прямые параллелепипеды со сторонами, параллельными осям координат x, у, z. Решение задач получаем методом сечения, в качестве секущих выбираем плоскости, параллельные какой-либо одной координатной плоскости: x—у, x—z или у—z. В результате трехмерная задача сводится к набору соответствующих плоских задач, решаемых по методике, которая приведена в п. 8, и затем объединяемых по формулам типа (17), (18), что дает решение исходной задачи. Аналогично, т.е. понижением размерности пространства с помощью метода сечений, решаются задачи 1 и 2 анализа изображения в пространствах произвольной размерности N.
* * *
Представленные задачи анализа изображении в пространствах различной размерности, эффективно решаемые с помощью автоматного моделирования в сочетании с аппаратом НЛ, свидетельствуют о пользе применения данного метода при решении многих других задач передачи и переработки информации, таких, как распознавание образов, анализ сцен, синхронизация параллельно работающих объектов и т.д.
Список литературы
1. Левин В.И. Непрерывная логика и ее применение // Информационные технологии, 1997. №1. С. 17—22.
2. Левин В.И. Введение в динамическую теорию конечных автоматов. Рига: Зинатне, 1975. 376 с.
3. Левин В.И. Динамика логических устройств и систем. М. Энергия, 1980. 224 с.
4. Левин В.И. Теория динамических автоматов. Пенза: Изд-во Пен7з. гос. техн. ун-та, 1995. 408 с.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ №8. 1997
ИНТЕЛЛЕКТУАЛЬНЫЕ СИТЕМЫ
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



