научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2012
DOI: 10.7463/1112.0496367
УДК 539.3
Россия, Саратов, СГУ им. Н.Г. Чернышевского
Россия, МГТУ им. Н.Э. Баумана
Введение
Исследование динамики покрытий является актуальной задачей, имеющей многочисленные приложения в современной науке и технике [1, 2]. Несмотря на то, что аналитическое решение может быть сравнительно легко записано, его дальнейший анализ существенно затруднен, оставляя возможность лишь для численного исследования. В этой связи одним из основных подходов к задаче остается получение приближенных граничных условий на границе основы и покрытия, в результате чего исследование сводится к более простой задаче для упругого полупространства, с приведенными граничными условиями, учитывающими свойства материала покрытия.
В классической работе [3] приведенные граничные условия были получены на основе физических гипотез. Более строго они могут быть выведены на основе метода прямого асимптотического интегрирования, разработанного А.Л. Гольденвейзером, см. [4-7]. Следует также отметить, что отсутствие должной математической строгости может привести к неточностям, см. например, [8], которые отразились и в последующих работах [9], [10]. В то же время в [11] показано, что слагаемые, за счет которых «уточняются» граничные условия [3], относятся к более высокому порядку малости, чем порядок предлагаемой в [8] приближенной теории.
Целью настоящей работы является вывод на основе метода асимптотического интегрирования приведенных граничных условий на поверхности контакта упругой полуплоскости и вязкоупругого покрытия. Следует отметить, что метод асимптотического интегрирования успешно применялся ранее для вязкоупругих тонкостенных конструкций [12, 13]. В данной работе получено длинноволновое приближение для неоднородных граничных условий на поверхности покрытия. Это позволит в дальнейшем не только использовать их для построения эффективного приближения дисперсионного соотношения, но и построить на их базе асимптотическую модель для волны Рэлея, расширяя подход, ориентированный на выделение вклада поверхностных волн в общую динамическую картину [11, 14, 15], на случай упругого полупространства с вязкоупругим покрытием.
1. Постановка задачи
Рассмотрим упругую изотропную полуплоскость с тонким вязкоупругим покрытием постоянной толщины ![]() . Введем прямоугольную декартову систему координат следующим образом: предположим, что ось
. Введем прямоугольную декартову систему координат следующим образом: предположим, что ось ![]() лежит на поверхности покрытия, а ось
лежит на поверхности покрытия, а ось ![]() направлена вниз, так, что граница раздела между основанием и покрытием задается уравнением
направлена вниз, так, что граница раздела между основанием и покрытием задается уравнением ![]() .
.
Уравнения движения в выбранной системе координат имеют вид:
 ,
,  , (1.1)
, (1.1)
где ![]() - компоненты вектора перемещения,
- компоненты вектора перемещения, ![]() - компоненты тензора напряжений,
- компоненты тензора напряжений, ![]() - плотность материала. Уравнения состояния для упругой полуплоскости примем в виде:
- плотность материала. Уравнения состояния для упругой полуплоскости примем в виде:
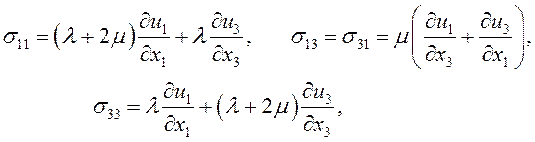 (1.2)
(1.2)
где ![]() и
и ![]() - постоянные Ламе. Скорости волн расширения и сдвига определяются выражениями
- постоянные Ламе. Скорости волн расширения и сдвига определяются выражениями
 и
и  . (1.3)
. (1.3)
Уравнения состояния для вязкоупругого изотропного материала возьмем в интегрально-операторной форме
 (1.4)
(1.4)
где ![]() и
и ![]() - интегральные операторы, задаваемые формулами
- интегральные операторы, задаваемые формулами
 , (1.5)
, (1.5)
 .
.
Здесь ![]() и
и ![]() - постоянные материала покрытия,
- постоянные материала покрытия, ![]() и
и ![]() - ядра релаксации.
- ядра релаксации.
Предположим, что на поверхности ![]() действует нормальная нагрузка
действует нормальная нагрузка ![]() , тогда граничные условия запишутся следующим образом:
, тогда граничные условия запишутся следующим образом:
![]() ,
, ![]() при
при ![]() . (1.6)
. (1.6)
Кроме того, мы будем принимать во внимание условие непрерывности перемещений и напряжений при ![]() .
.
2. Приведенные граничные условия
Рассмотрим задачу для вязкоупругого покрытия, задавая на границе ![]() условия:
условия:
![]() , (2.1)
, (2.1)
где ![]() - заданные перемещения,
- заданные перемещения, ![]() .
.
Применим к задаче (1.1), (1.2), (1.4) стандартную схему асимптотического интегрирования, см. например, [4-7, 11]. В случае покрытия ![]() , все параметры материала обозначим индексом '0'. Введем малый геометрический параметр
, все параметры материала обозначим индексом '0'. Введем малый геометрический параметр
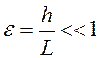 , (2.2)
, (2.2)
соответствующий предположению о длинноволновом приближении, где ![]() - характерная длина волны. Введем безразмерные переменные
- характерная длина волны. Введем безразмерные переменные
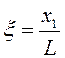 ,
,  ,
, 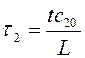 , (2.3)
, (2.3)
где  ,
, ![]() - плотность материала покрытия. Также введем безразмерные величины
- плотность материала покрытия. Также введем безразмерные величины
 ,
, 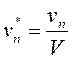 ,
,  ,
,  ,
,  , (2.4)
, (2.4)
где ![]() - максимальная амплитуда перемещений и предполагается, что величины со звездочкой одного асимптотического порядка.
- максимальная амплитуда перемещений и предполагается, что величины со звездочкой одного асимптотического порядка.
Уравнения движения и состояния в безразмерных переменных принимают вид
 ,
,
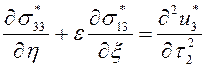 ,
,
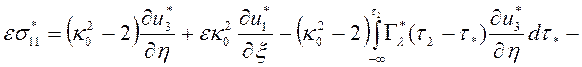
 , (2.5)
, (2.5)
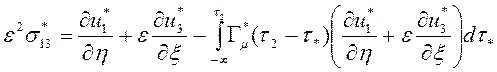 ,
,
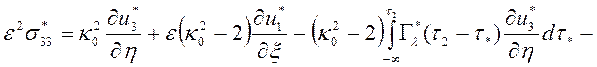
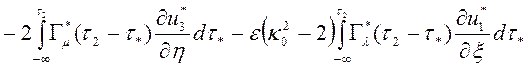 ,
,
где 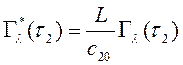 ,
, 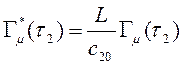 ,
, 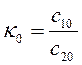 ,
,  .
.
Граничные условия в безразмерной форме имеют вид:
![]() ,
, ![]() при
при ![]() ,
, ![]() при
при ![]() . (2.6)
. (2.6)
Разложим перемещения и напряжения в ряды по малому параметру ![]() :
:
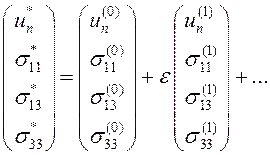 . (2.7)
. (2.7)
Подставляя эти ряды в уравнения (2.5) и граничные условия (2.6), и приравнивая коэффициенты при ![]() , получаем систему для определения компонент ведущего порядка
, получаем систему для определения компонент ведущего порядка
 ,
,
 ,
,
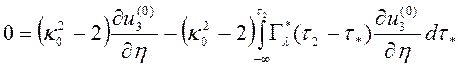 , (2.8)
, (2.8)
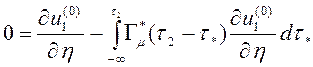 ,
,
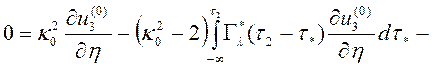
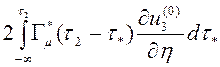 ,
,
![]() при
при ![]() ,
,
![]() при
при ![]() ,
,
![]() при
при ![]() .
.
Интегрируя уравнения (2.8)4 и (2.8)5 совместно с граничными условиями (2.8)6, а также уравнение (2.8)2 совместно с граничным условием (2.8)7, найдем
![]() ,
, 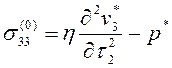 (2.9)
(2.9)
Последняя формула дает главный член искомого значения нормального напряжения ![]() .
.
Из уравнения (2.5)4 получим:
 , (2.10)
, (2.10)
откуда,
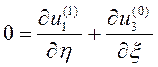 . (2.11)
. (2.11)
Из граничных условий (2.6) имеем
![]() при
при ![]() , (2.12)
, (2.12)
следовательно,
 . (2.13)
. (2.13)
Аналогично, из (2.5)5, с учетом граничного условия (2.12)
 , (2.14)
, (2.14)
где I– тождественный оператор и
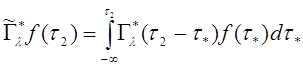 ,
, 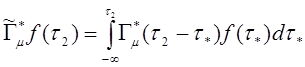 . (2.15)
. (2.15)
Используя формулы (2.5)3, (2.9) и (2.14), находим
 (2.16)
(2.16)
Подставляя (2.16) в (2.8)1, учитывая (2.8)8, получим выражение для ![]() – главного члена в разложении
– главного члена в разложении ![]() :
:
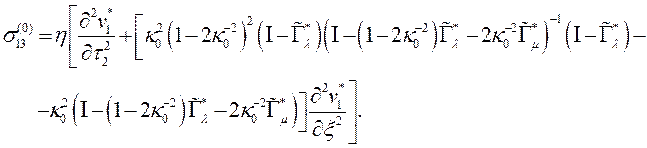 (2.17)
(2.17)
Возвращаясь к исходным переменным, запишем приведенные граничные условия на поверхности контакта ![]() :
:
 (2.18)
(2.18)
где
 .
.
Заключение
В данной работе в рамках длинноволнового приближения получены эффективные граничные условия для системы «упругая основа – вязкоупругое покрытие» для случая заданных на поверхности покрытия нормальных усилий. В дальнейшем результаты (2.18) могут быть использованы для анализа поля волны Рэлея в случае заданного типа нагрузки на поверхности, см. [11], а также исследования распространения поверхностной волны в зависимости от параметров материала вязкоупругого покрытия. При этом возможность рассмотрения динамической задачи обеспечивается тонкостью покрытия.
Авторы выражают свою искреннюю благодарность д.ф.-м.н., проф. Каплунову Ю.Д. за плодотворные обсуждения. Исследования Анофриковой Н.С. поддержаны грантом РФФИ № 11-01-00545-a. Исследования Приказчикова Д.А. выполнены при поддержке РФФИ, грант № 12-01-33049.
Список литературы
1. Shuvalov A.L., Every A.G. On the long-wave onset of dispersion of the surface-wave velocity in coated solids // Wave Motion. 2008. Vol. 45, no. 6. P. 857-863. DOI: http://dx.doi.org/10.1016/j.wavemoti.2007.12.002
2. Захаров Д.Д. Эффективные аппроксимации высокого порядка для слоистых покрытий и прослоек из анизотропных упругих, вязкоупругих и нематических материалов // Прикладная математика и механика. 2010. Т. 74, № 3. С. 403-418.
3. Tiersten H.F. Elastic surface waves guided by thin films // J. Appl. Phys. 1969. Vol. 40. P. 770-789.
4. Гольденвейзер А. Л. Построение приближенной теории изгиба пластинки методом асимптотического интегрирования уравнений теории упругости // Прикладная математика и механика. 1962. Т. 26, № 4. С. 662-686.
5. Гольденвейзер А.Л. Теория упругих тонких оболочек. М.: Наука, 1976. 510 с.
6. Goldenveiser A.L., Kaplunov J.D., Nolde E.V. On Timoshenko-Reissner type theories of plates and shells // Int. J. Solids Struct. 1993. Vol. 30. P. 675-694.
7. Kaplunov J.D., Kossovich L.Yu., Nolde E.V. Dynamics of Thin Walled Elastic Bodies. N.-Y.: Academic Press, 1998. 226 p.
8. Bovik P. A comparison between the Tiersten model and O(h) boundary conditions for elastic surface waves guided by thin layers // ASME J. Appl.Mech. 1996. Vol. 63. P. 162-167.
9. Niklasson J., Datta S.K., Dunn M.L. On approximating guided waves in plates with thin anisotropic coating by means of effective boundary conditions // J. Acoust. Soc. Am. 2000. Vol. 108. P. 924-933.
10. Vinha P.C., Linhb N.T.K. An approximate secular equation of Rayleigh waves propagating in an orthotropic elastic half-space coated by a thin orthotropic elastic layer // Wave Motion. 2012. Vol. 49, № 7. P. 681-689. DOI: http://dx.doi.org/10.1016/j.wavemoti.2012.04.005
11. Dai H.-H., Kaplunov J., Prikazchikov D.A. A long-wave model for the surface elastic wave in a coated half-space // Proc. Roy. Soc. A. 2010. Vol. 466. P. 3097-3116.
12. Anofrikova N.S., Kossovich L.Yu., Kirillova I.V., Shevtsova Yu.V. Non-stationary waves in thin walled bodies at shock loading: asymptotic approach // Topical Problems in Solid and Fluid Mechanics. Elite Publishing House Ltd., 2011. P. 318-330. ISBN 81-88901-43-1.
13. Бажанова Н.С., Коссович Л.Ю., Сухоловская М.С. Нестационарные волны в вязкоупругих оболочках: модель Максвелла // Изв. ВУЗов Сев.-Кавк. региона. Естественные науки. 2000. № 2. С. 17-24.
14. Kaplunov J., Zakharov A., Prikazchikov D.A. Explicit models for elastic and piezoelastic surface waves // IMA J. Appl. Math. 2006. Vol. 71. P. 768-782.
15. Приказчиков Д.А. Развитие асимптотических моделей для поверхностных и интерфейсных волн // Вестник НГУ им. Н.И. Лобачевского. 2011. Т. 4, № 4. С. 1713-1715.
Публикации с ключевыми словами: приведенные граничные условия, асимптотическое интегрирование, вязкоупругое покрытие
Публикации со словами: приведенные граничные условия, асимптотическое интегрирование, вязкоупругое покрытие
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



