научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2012
DOI: 10.7463/1112.0496336
УДК 539.3
Россия, МГТУ им. Н.Э. Баумана
Введение. Современные композиционные материалы, как правило, обладают явно выраженной многомасштабной иерархической структурой, в которой каждый последующий структурный уровень, содержит предыдущий уровень. Особенно четко такая структура реализуется в композитах на основе армирующих волокон различного переплетения: тканевого, намоточного, пространственного, у которых сами волокна представляют собой пучки большого числа моноволокон [1]. Традиционные методы расчета [2-3] прочностных характеристик таких композитов основаны на приближенно-аналитических подходах, которые, как правило, приводят к приемлемым результатам при расчете прочности в направлении армирования, но обладают значительной погрешностью при расчете прочностных характеристик в поперечных направлениях и при сдвиге.
Значительный успех в проблеме расчета характеристик композитов был достигнут после создания метода гомогенизации или осреднения и разработки эффективных вычислительных алгоритмов решения локальных задач, возникающих в этом методе [4-7]. В работах [8-10] разработаны вычислительные технологии решения локальных задач на ячайках периодичности, которые возникают в этом методе. Решение данных задач методом конечных элементов является достаточно ресурсоемким и потребовало создания высокопроизводительной распределенной программной системы, которая бы обеспечила информационно-вычислительную поддержку процессов совместного проектирования новых композиционных материалов и конструкций на их основе. Теоретические основы метода гомогенизации применительно к различным микроструктурам упругих композитов изложены в [11]. Целью настоящей работы являлось применение метода микроструктурного конечно-элементного анализа для расчета поверхностей прочности композитов, экспериментальное определение которых, как правило, представляет собой сложную техническую проблему.
Метод расчета поверхностей прочности композитов. Для расчета поверхностей прочности композитов (КМ) предлагается следующий метод, состоящий из 4-х основных этапов.
1. Согласно методу гомогенизации [7, 11] осуществляется решение серии так называемых локальных задач ![]() теории упругости на 1/8 ячейке периодичности композита
теории упругости на 1/8 ячейке периодичности композита ![]() ,
,
 (1)
(1)
где ![]() - поверхности контакта компонентов композита,
- поверхности контакта компонентов композита, ![]() - координатные плоскости,
- координатные плоскости, ![]() ,
, ![]() - торцовые поверхности.
- торцовые поверхности. ![]() ,
, ![]() ,
, ![]() - перемещения, напряжения и деформации в компонентах композита
- перемещения, напряжения и деформации в компонентах композита ![]() ,
, ![]() ;
; ![]() - тензоры модулей упругости компонентов,
- тензоры модулей упругости компонентов, ![]() - локальные координаты,
- локальные координаты, ![]() - производные по локальным координатам. Функции
- производные по локальным координатам. Функции ![]() удовлетворяют следующим граничным условиям на
удовлетворяют следующим граничным условиям на ![]() :
:
- при
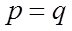 ,
,
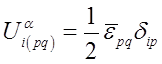 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (2)
(2)
- при
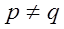 ,
,
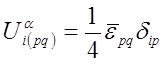 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; (3)
; (3)
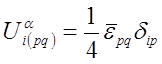 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
где ![]() - средние значения деформации композита (заданы). Решение задач (1)-(3) ищется с помощью метода конечного элемента [12].
- средние значения деформации композита (заданы). Решение задач (1)-(3) ищется с помощью метода конечного элемента [12].
2. После решения серии задач ![]() для всех
для всех ![]() ,
, ![]() вычисляются эффективные упругие модули композита по следующим формулам:
вычисляются эффективные упругие модули композита по следующим формулам:
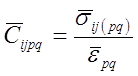 ,
, 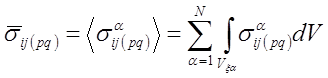 ,
, 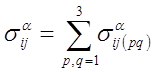 (4)
(4)
3. Далее вычисляется тензор эффективных упругих податливостей ![]() и по его компонентам - технические константы:
и по его компонентам - технические константы: ![]() - модули Юнга,
- модули Юнга, ![]() - коэффициенты Пуассона,
- коэффициенты Пуассона, ![]() - модули сдвига (здесь по
- модули сдвига (здесь по ![]() ,
, ![]() суммирования нет). Затем вычисляем компоненты тензора концентрации напряжений:
суммирования нет). Затем вычисляем компоненты тензора концентрации напряжений: ![]() , связывающие напряжения в компонентах композита с осредненными напряжениями:
, связывающие напряжения в компонентах композита с осредненными напряжениями: ![]() . Это соотношение удобно переписать в матричном виде, введя следующие обозначения для групп индексов:
. Это соотношение удобно переписать в матричном виде, введя следующие обозначения для групп индексов: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() :
:
![]() , (5)
, (5)
4. Одним из наиболее широко применяемых на практике способов моделирования поверхностей прочности анизотропных материалов является использование квадратичного критерия прочности Малмейстера-Ву. Положим, что разрушение в точке ![]() компонента композита наступает, если в этой точке выполняется критерий Малмейстера –Ву:
компонента композита наступает, если в этой точке выполняется критерий Малмейстера –Ву:
 ,
, ![]() , (6)
, (6)
где![]() - матрицы и векторы констант прочности
- матрицы и векторы констант прочности ![]() -й компоненты композита (заданы), они имеют по 9 и 3 независимых компонент соответственно.
-й компоненты композита (заданы), они имеют по 9 и 3 независимых компонент соответственно.
Подставляя (5) в (6), получим
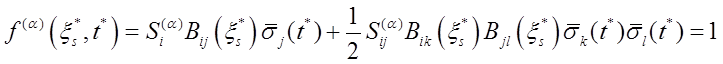 (7)
(7)
где ![]() - момент времени разрушения компоненты композита в точке
- момент времени разрушения компоненты композита в точке ![]()
5. Зададим теперь серию из M законов изменения компонент средних напряжений ![]() в виде линейной функции от времени нагружения t:
в виде линейной функции от времени нагружения t: ![]() ,
, ![]() . Для каждого
. Для каждого ![]() элемента серии осуществляется нагружение композита с заданным вектором
элемента серии осуществляется нагружение композита с заданным вектором ![]() при изменяющемся t от 0 до
при изменяющемся t от 0 до ![]() . Осуществляется итерационное приращение аргумента t и на каждом шаге итерации проверяется выполнение условия
. Осуществляется итерационное приращение аргумента t и на каждом шаге итерации проверяется выполнение условия ![]() . Как только при некотором
. Как только при некотором ![]() впервые выполняется условие
впервые выполняется условие ![]() , происходит разрушение компонента композита. Полагается, что это разрушение и есть разрушение композита в целом. В результате в численном эксперименте находятся значения
, происходит разрушение компонента композита. Полагается, что это разрушение и есть разрушение композита в целом. В результате в численном эксперименте находятся значения ![]() и
и ![]() .
.
5) Будем далее аппроксимировать поверхность прочности композита с помощью того же квадратичного критерия прочности Малмейстера-Ву, но с заранее неизвестными константами ![]()
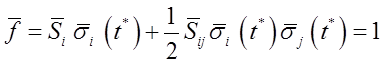 , (8)
, (8)
Осуществляя далее всю серию из M нагружений с различными значениями ![]() в каждом нагружении, на основе (8) можно составить систему уравнений
в каждом нагружении, на основе (8) можно составить систему уравнений
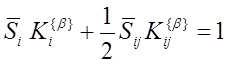 ,
,![]() (9)
(9)
где ![]() - найденные к данному этапу величины. Полагая М=12, систему (9) можно рассматривать как систему линейных алгебраических уравнений относительно 12 констант
- найденные к данному этапу величины. Полагая М=12, систему (9) можно рассматривать как систему линейных алгебраических уравнений относительно 12 констант ![]() . Решая эту СЛАУ, находим константы прочности композита в целом.
. Решая эту СЛАУ, находим константы прочности композита в целом.
Применялся также другой способ нахождения констант прочности ![]() - из условия наилучшей аппроксимации экспериментально получаемой поверхности прочности композита в 6-мерном пространстве осредненных компонент тензора напряжений
- из условия наилучшей аппроксимации экспериментально получаемой поверхности прочности композита в 6-мерном пространстве осредненных компонент тензора напряжений ![]() .
.
Результаты численного моделирования. Численные расчеты проводились для дисперсно-армированного КМ, структура которого представлена на рисунке 1. Исходные данные: матрица изотропная (алюминиевый сплав)- ![]() ГПа,
ГПа, ![]() , пределы прочности при растяжении, сжатии и сдвиге
, пределы прочности при растяжении, сжатии и сдвиге ![]()
![]() ,
, ![]() ; армирующий наполнитель – в виде сферических частиц с константами упругости (карбид кремния)
; армирующий наполнитель – в виде сферических частиц с константами упругости (карбид кремния) ![]() ГПа,
ГПа, ![]() и пределами прочности
и пределами прочности ![]()
![]() ,
, ![]() . По пределам прочности вычислялись значения констант прочности
. По пределам прочности вычислялись значения констант прочности![]() .
.
Были получены следующие значения эффективных упругих констант композита: ![]() ГПа,
ГПа, ![]() ,
, ![]() ГПа. Число конечных элементов, на которые разбивалась ЯП, равно 4773. На рис. 1-2 показаны распределения напряжений
ГПа. Число конечных элементов, на которые разбивалась ЯП, равно 4773. На рис. 1-2 показаны распределения напряжений ![]() в ЯП как результат решения локальных задач
в ЯП как результат решения локальных задач ![]() .
.
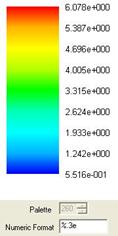
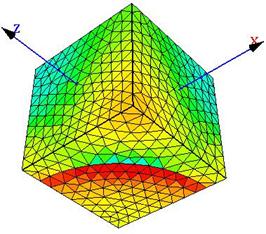
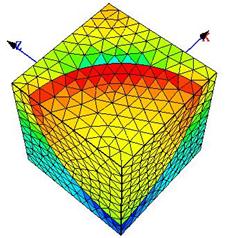
Рис. 1. – Сдвиговые напряжения ![]() , Мпа
, Мпа
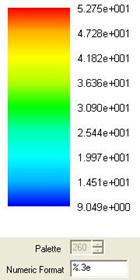
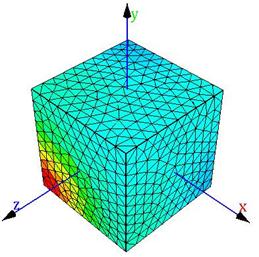
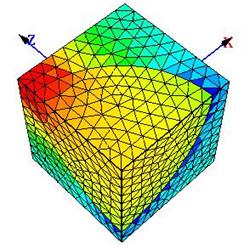
Рис. 2. – Нормальные напряжения ![]() в ЯП, МПа
в ЯП, МПа
С помощью изложенного выше алгоритма были получены прочностные характеристики исследуемого КМ: ![]() ,
, ![]() ,
, ![]() , а также следующая матрица прочности композита:
, а также следующая матрица прочности композита:
 ,
,
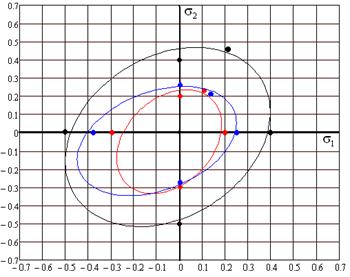
На рис. 3 показаны сечения поверхности прочности матрицы, армирующего наполнителя и композита. Точками показаны «точные» численные значения прочности, а линиями – аппроксимация с помощью критерия Малмейтера-Ву. Получено достаточно хорошее качество аппроксимации.
|
|
Рис. 3. – Сечение поверхностей прочности компонент композита и самого КМ, ГПа | Рис. 4. – Распределение компонент тензоров концентрации напряжений B1212 и B1111 для дисперсно-армированного КМ с учетом поверхности раздела |
Были также проведены численные расчеты для случая дисперсно-армированного композита, для которого учитывалась поверхность раздела матрицы и наполнителя. Для этой цели вводился дополнительный 3-й элемент в ЯП. Геометрическая структура такого композита показана на рис. 4, а некоторые результаты расчетов задачи Lpq - на рис. 5.
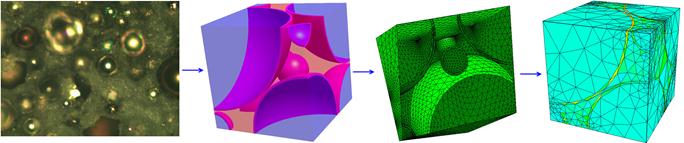
Рис. 5. – Реальная микроструктура дисперсно-армированного композита на основе эластомерной матрицы и стеклянных микросфер, компьютерная модель микроструктуры и конечно-элементная сетка композита, использованная в расчетах
Были также проведены расчеты для тканевых композиционных материалов с сатиновым типом переплетения (рис. 6 а, б).
|
|
Рис. 6 а) – Конечно-элементная аппроксимация расчетной области для тканевого КМ | Рис. 6 б) – Распределение поля компоненты |
На рис. 7 показаны результаты численного моделирования задачи о напряженно-деформированном состоянии для ячейки периодичности тканевого КМ с сатиновым типом переплетения.
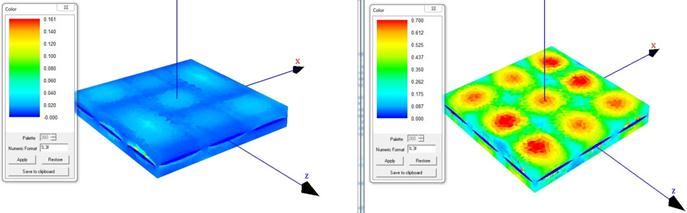
Рис. 7. – Поля функции повреждаемости в при решении задач: сдвига в плоскости XY (слева) и растяжения по оси Y (справа) для тканевого КМ
Выводы. Разработан математический метод и вычислительная технология расчета прочностных характеристик КМ, в основе которого лежит использование квадратичного критерия прочности Малмейстера-Ву. Показано, что предложенный метод является достаточно эффективным с вычислительной точки: он позволяет прогнозировать поверхность прочности композита, используя только одну итерацию решения локальных задач Lpq. В то же время, следует отметить, что описанный метод нуждается в модифицировании при расчете не начальной поверхности прочности композита, которая фактически и находится этим методом, а предельной поверхности прочности, когда нагружение осуществляется до полного разрушения композита. В этом случае необходимо многократное решение задач Lpq на каждом шаге цикла нагружения, учитывая при этом изменение зоны разрушения компонентов композита.
Благодарности. Работа проведена при финансовой поддержке Министерства образования и науки Российской Федерации по Соглашению о предоставлении гранта в форме субсидии №14.B37.21.1869 от "04" октября 2012 г. в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы.
Список литературы
1. Композиционные материалы: Справочник / Под ред. В.В. Васильева, Ю.М. Тарнопольского. М.: Машиностроение, 1989. 510 с.
2. Малмейстер А.К., Тамуж В.П., Тетерс Г.А.Сопротивление полимерных и композитных материалов. Рига: Зинатне, 1980. 572 с.
3. Тарнопольский Ю.М., Жигун И.Г., Поляков В.А. Пространственно-армированные композиционные материалы. М.: Машиностроение, 1987. 225 с.
4. Бахвалов Н.С., Панасенко Г.П. Осреднение процессов в периодических средах. М.: Наука, 1984. 352 c.
5. Победря Б.Е. Механика композиционных материалов. М.: МГУ, 1984. 336 с.
6. Санчес-Паленсия Э. Неоднородные среды и теория колебаний : пер. с англ. М.: Мир, 1984. 471 с.
7. Димитриенко Ю.И. Механика композиционных материалов при высоких температурах. М.:Машиностроение, 1997. 356 с.
8. Димитриенко Ю.И., Соколов А.П. Разработка автоматизированной технологии вычисления эффективных упругих характеристик композитов методом асимптотического осреднения // Вестник МГТУ им. Н.Э.Баумана. Сер. Естественные науки. 2008.№2. С. 57-67.
9. Димитриенко Ю.И., Соколов А.П. Автоматизация прогнозирования свойств композиционных материалов на основе метода асимптотического осреднения // Информационные технологии. 2008. № 8. С. 31-38.
10. Соколов А.П., Шпакова Ю.В., Першин А.Ю. Проектирование и разработка распределенной вычислительной системы инженерного анализа свойств композиционных материалов // Материалы IX Международной конференции по неравновесным процессам в соплах и струях (NPNJ’2012). Алушта, Украина: Московский Авиационный Институт, 2012. С. 518-521.
11. Димитриенко Ю.И., Соколов А.П. Об упругих свойствах композиционных материалов // Математическое моделирование. 2009. Т.21, №4. С. 96-110.
12. Димитриенко Ю.И., Кашкаров А.И. Конечно-элементный метод для вычисления эффективных характеристик пространственно-армированных композитов // Вестник МГТУ им. Н.Э.Баумана. Сер. Естественные науки. 2002. № 2. C. 95-108.
Публикации с ключевыми словами: метод конечных элементов, метод асимптотического осреднения, многомасштабные структуры, эффективные упруго-прочностные характеристики, поверхности прочности, тканевые композиционные материалы
Публикации со словами: метод конечных элементов, метод асимптотического осреднения, многомасштабные структуры, эффективные упруго-прочностные характеристики, поверхности прочности, тканевые композиционные материалы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||