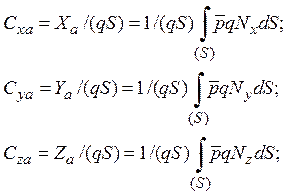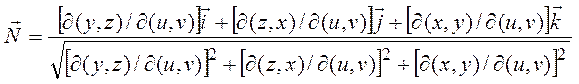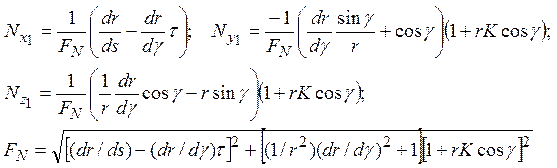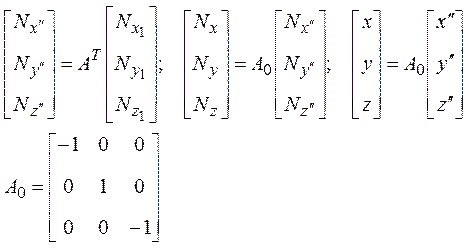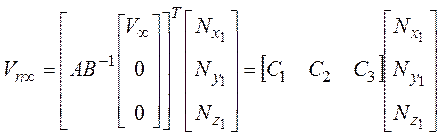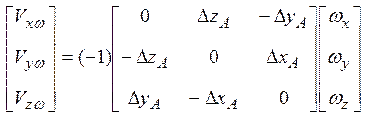научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2012
DOI: 10.7463/1112.0492155
УДК 623.5 (533.696.3)
Россия, МГТУ им. Н.Э. Баумана
Рассмотрим класс летательных аппаратов, с необратимыми деформациями корпуса в виде произвольно искривленной оси. Актуальной является задача разработки методики расчета аэродинамических коэффициентов таких тел.
Одной из главных компонент аэродинамических нагрузок является составляющая, обусловленная действием сил давления (см. [1]). Ряд приближенных методов ее определения, о которых говорилось в данной статье, оказался по тем или иным причинам непригодным для исследуемого класса тел - искривленных, с большими величинами деформаций. Так, форма исследуемого объекта не позволяет применять в полной мере методы касательных конусов, а точность метода течений разрежения - скачков уплотнения ухудшается с ростом углов атаки, ибо при этом начинает сказываться влияние вязкости, отрывных течений, а также ухудшение использования предположения о плоских течениях в каждой меридиональной плоскости.
В результате анализа существующих методов, проведенной в [1] за основу была взята гипотеза "ньютонова торможения". Она обычно применяется для приближенного расчета давления при больших скоростях обтекания. Согласно корпускулярной теории Ньютона частицы газа испытывают возмущения только при ударе о твердую стенку и полностью теряют нормальную к стенке составляющую количества движения. С физической точки зрения при обтекании тела с большой сверхзвуковой скоростью предположение Ньютона становится справедливым [2], так как в этом случае ударная волна располагается близко к поверхности тела и все струйки до ударной волны имеют одинаковые направления и величину скорости невозмущенного потока, а за ударной волной движутся в тонком слое между нею и телом и приобретают почти одинаковые скорости, параллельные его поверхности. Чем больше число Маха и тоньше тело, тем ближе к действительности теория Ньютона. Указанная причина объясняет достаточно хорошую сходимость расчета и реального распределения давления, увеличивающуюся по мере роста числа Маха и практический расчет дает во многих случаях удовлетворительные результаты, несмотря на то, что влияние вязкости в теории Ньютона не учитывается. Для повышения точности расчетов в общепринятую формулу, выражающую давление через квадрат синуса угла наклона тела без поправки на центробежные силы, вводится некоторый множитель, учитывающий точное значение давления торможения» Предложенная Лизом формула носит название ньютоновой модифицированной и носит эмпирический характер.
Пределы применения теории с учетом различных модификаций даже в случае исследования нестационарного обтекания (γ - коррекция) могут быть расширены до 2-3, причем, как показано в [1] (сравнение с теорией поперечного обтекания), теория может применяться и при больших отклонениях потока. Взятая за основную физическую гипотезу при разработке методики определения стационарных и нестационарных характеристик - составляющих от распределения сил давления гипотеза ньютонова торможения была в [1] проверена экспериментально для исследуемых искривленных тел путем сравнения с расчетными зависимостями значений коэффициентов давления на поверхности тела и суммарных аэродинамических и была подтверждена возможность ее применения.
В соответствии с указанной гипотезой распределение давления на теле определяется по формуле через коэффициент давления:
| (1) |
где η - угол между направлением набегающего потока и нормалью к поверхности тела, индекс ∞ относится к параметрам набегающего потока; V∞ - скорость набегающего потока (модуль), ρ – плотность, q∞ - скоростной напор.
Рассматриваются две составляющие вектора скорости набегающего потока: от поступательного движения ![]() и от вращательного движения вокруг центра масс со скоростью
и от вращательного движения вокруг центра масс со скоростью ![]() :
: ![]() . Тогда коэффициент давления будет состоять из двух членов, определяемых нормальными частями указанных составляющих, так что (1) запишется в виде:
. Тогда коэффициент давления будет состоять из двух членов, определяемых нормальными частями указанных составляющих, так что (1) запишется в виде:
| (2) |
где индекс "отн." определяет относительную скорость частицы газа, равную переносной скорости точки тела, в которой определяется давление, взятой с обратным знаком. Основной задачей, как следует из формул для коэффициента давления, является определение нормали к поверхности, тогда можно определить и составляющие нормальной скорости, а значит, и коэффициент ![]() .
.
Приведем общие соотношения для скоростей, давлений, сил и моментов.
Нормальные составляющие скоростей получаются скалярным перемножением вектора соответствующей скорости на вектор единичной нормали:
| (3) |
где Vxω, Vyω, Vzω- компоненты вектора поточной скорости в некоторой системе XYZ;
Nx, Ny, Nz-компоненты вектора единичной нормали к поверхности в той же системе.
Заметим, что в связанной обращенной системы координат (в дальнейшем обозначим X"Y"Z") для представления компонент вектора скорости набегающего потока через углы атаки αи скольжения βизвестные формулы:
| (4) |
где ![]() - единичные орты системы X"Y"Z".Угловая скорость вращательного движения:
- единичные орты системы X"Y"Z".Угловая скорость вращательного движения:
![]()
Добавочная скорость обращенного движения, индуцируемая в рассматриваемой точке А, равна векторному произведению:
| (5) |
Нормальная составляющая этой скорости определяется как скалярное произведение вектора (5) на вектор нормали:
![]()
где компоненты скорости получаются из раскрытия векторного произведения.
Заметим, что начало координат используемой системы может не совпадать с центром масс тела, относительно которого осуществляется вращение. Рассмотрим некоторую точку А, принадлежащую деформированному телу, с радиусом-вектором от начала координат до этой точки ![]() и точку центра масс тела с радиусом
и точку центра масс тела с радиусом ![]() . Тогда вектор, соединяющий точки А и центра масс и направленный к точке А, обозначим
. Тогда вектор, соединяющий точки А и центра масс и направленный к точке А, обозначим ![]() , и подставим в вышеприведенную формулу:
, и подставим в вышеприведенную формулу:
| (6) |
Для определения аэродинамических коэффициентов рассмотрим силу, действующую на элемент поверхности и порождаемую нормальным давлением:
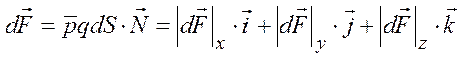
Выполняя интегрирование по поверхности для каждой из компонент и относя к характерной площади и скоростному напору согласно общим выражениям
![]()
имеем формулы для аэродинамических коэффициентов в некоторой системе координат XYZ:
| (7) |
где Nx, Ny, Nz- проекции нормали на оси координат x,y,z;
![]() - местный коэффициент давления, действующий на данную площадку dS и рассчитываемый по формуле (2);
- местный коэффициент давления, действующий на данную площадку dS и рассчитываемый по формуле (2);
q- скоростной напор.
Момент силы ![]() относительно центра O равен векторному произведению радиуса-вектора
относительно центра O равен векторному произведению радиуса-вектора ![]() , соединяющего этот центр с точкой приложения силы А на эту силу:
, соединяющего этот центр с точкой приложения силы А на эту силу:
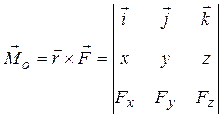
Рассматривая момент от элементарной силы dFи учитывая выражения компонент силы по осям координат5после раскрытия определителя формулы для Moимеем:
![]()
где ![]() .
.
Отсюда, используя формулы (3) имеем выражения для аэродинамических коэффициентов моментов:
| (8) |
Пределы интегрирования зависят в случае использования метода Ньютона от геометрии тела и параметров его движения. Чтобы установить их, надо исходить из особенностей обтекания тела "ньютоновым потоком": на его поверхности создается некоторая «затененная» зона, в которой не происходит удара частиц.
Граница этой области определяется кривой, на которой, как и всюду за ней, коэффициент давления равен нулю. Из выражения для коэффициента давления ясно, что уравнение границы:
| (9) |
откуда и определяют пределы интегрирования.
Очевидно, что важнейшей проблемой является оптимальное задание геометрии искривленного тела и определение основных геометрических соотношений и связи между используемыми системами координат.
Рассмотрим задачу в наиболее общей постановке. Пусть задано тело произвольной формы. Эту форму можно определить, задав некоторую ось тела, тогда в каждом сечении, перпендикулярном этой оси, точка поверхности определится с помощью угла и радиуса - переменного по оси тела и в общем случае зависящего от этого угла. Тем самым мы используем так называемую цилиндрическую систему координат.
Предположим, что в результате деформаций сечения тела остались плоскими с теми же переменными радиусами, а ось его приобрела некоторую криволинейную пространственную форму. Геометрию нового деформированного тела наиболее удобно задать в криволинейной системе координат, задание которой естественно связать с положением в пространстве искривленной оси тела (рис. 1).
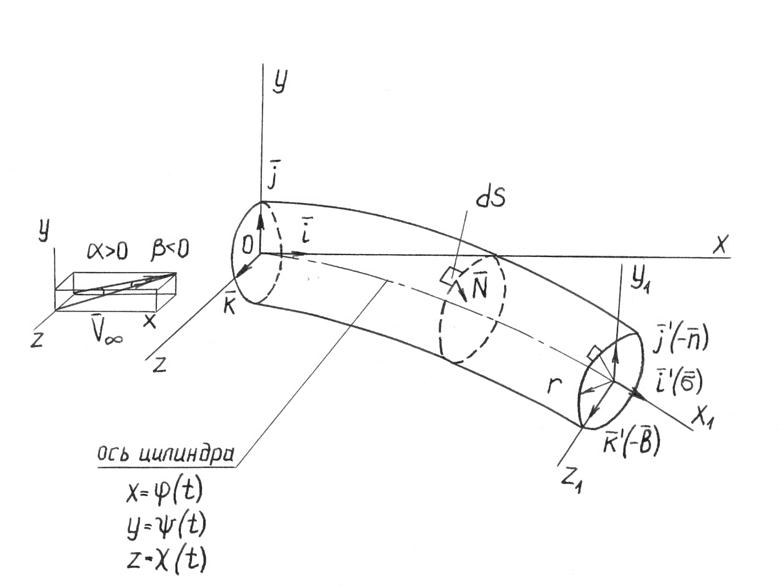
Рис. 1. Криволинейная система координат для искривленного тела
Уравнение линии в пространстве задается векторным уравнением:
![]()
где X,Y,Z - могут быть заданы как функции некоторого параметра t- например длины дуги s, так что
| (10) |
Известно, что пространственная кривая имеет ряд важных геометрических характеристик, таких как: положение касательной, нормали и бинормали в данной точке кривой.
При параметрическом задании пространственной кривой имеем:
1) касательная к кривой - единичный вектор:
| (11) |
2) единичный вектор главной нормали ![]() кривой с радиусом кривизны R и кривизной К = 1/R:
кривой с радиусом кривизны R и кривизной К = 1/R:
| (12) |
3) бинормаль для правой тройки орт
| (13) |
Эти вектора удобно брать в качестве орт криволинейной системы координат, направление которых в общем случае переменно по длине тела.
Перечислим системы координат, которыми будем далее пользоваться (рис. 2).
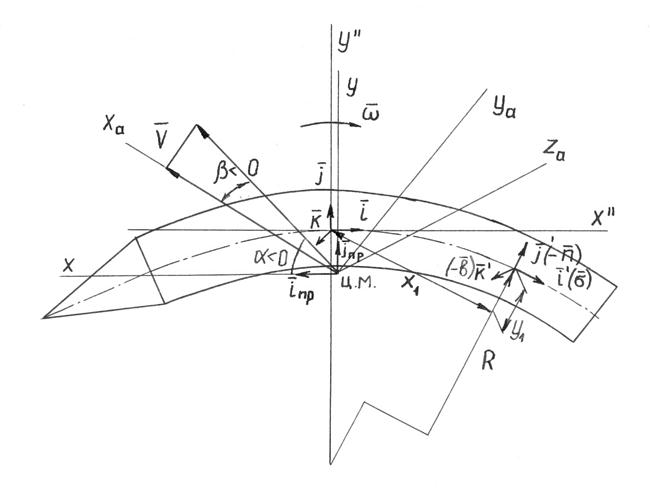
Рис. 2. Системы координат, используемые при выводе формул для искривленного тела.
Основная система координат OXYZ- связанная. Своим началом имеет действительный центр масс тела или какую-либо другую точку (в этом случае осуществляется пересчет получаемых соотношений). Ее орты ![]() ориентированы так, чтобы ось X была направлена к носку тела. Если тело имеет плоскость симметрии (в случае плоского искривления тела вращения), целесообразно в ней размещать оси OXOY. Используется также ряд вспомогательных систем координат. Система O"X"O"Y" имеет следующие свойства: начало координат расположено в произвольной точке, определяемой удобствами получения геометрических, инерционных и аэродинамических соотношений, например, в точке, где находился центр масс тела до деформации, или в сечении торцов. Орты этой системы
ориентированы так, чтобы ось X была направлена к носку тела. Если тело имеет плоскость симметрии (в случае плоского искривления тела вращения), целесообразно в ней размещать оси OXOY. Используется также ряд вспомогательных систем координат. Система O"X"O"Y" имеет следующие свойства: начало координат расположено в произвольной точке, определяемой удобствами получения геометрических, инерционных и аэродинамических соотношений, например, в точке, где находился центр масс тела до деформации, или в сечении торцов. Орты этой системы ![]() ориентированы так, что
ориентированы так, что ![]() . Система O1X1Y1Z1 является криволинейной. Ее начало - точка О1 - совпадает с точкой O". Направления орт
. Система O1X1Y1Z1 является криволинейной. Ее начало - точка О1 - совпадает с точкой O". Направления орт ![]() переменны по длине и выбраны:
переменны по длине и выбраны:
![]() - по касательной к искривленной оси в данной точке;
- по касательной к искривленной оси в данной точке;
![]() - против главной нормали в данной точке;
- против главной нормали в данной точке;
![]() - против бинормали (дополняет систему
- против бинормали (дополняет систему ![]() до правой)
до правой)
Тогда связь между ортами ![]() и
и ![]() соответственно исходной (O"X"O"Y") декартовой и криволинейной (O1X1Y1Z1) систем координат будет определяться соотношением:
соответственно исходной (O"X"O"Y") декартовой и криволинейной (O1X1Y1Z1) систем координат будет определяться соотношением:
| (14) |
где А - переходная матрица:
A(1,l) - первая строка матрицы - направляющие косинусы для касательной - коэффициенты при ортах ![]() в выражении для
в выражении для ![]() ;
;
A(2,l) - вторая строка матрицы - направляющие косинусы для противонормали - коэффициенты при ортах ![]() в выражении для
в выражении для ![]() ;
;
A(3,l) - третья строка матрицы - направляющие косинусы для противобинормали; l= 1,2,3.
При этом связь между компонентами в указанных системах координат ![]() (O"X"O"Y") и
(O"X"O"Y") и ![]() (O1X1Y1Z1) задается соотношением:
(O1X1Y1Z1) задается соотношением:
| (15) |
где А - ортогональная матрица, поэтому А-1 = АT .
Для описания геометрии тела и после деформации удобно использовать цилиндрическую систему координат, только она также будет криволинейной: s,r,γпричем теперь s- расстояние по дуге искривленной оси.
Поясним выбор этой системы координат. Выберем некоторую точку "С" на произвольно искривленной оси.
Ее радиус-вектор относительно исходной точки начала координат системы (O"X"O"Y") будет ![]() и имеет компоненты в системе O"X"O"Y":
и имеет компоненты в системе O"X"O"Y": ![]() . В системе O1X1Y1Z1- криволинейной, с тем же началом координат компоненты этого вектора
. В системе O1X1Y1Z1- криволинейной, с тем же началом координат компоненты этого вектора ![]() . Проведем через эту точку плоскость, перпендикулярную к касательной в этой точке оси. Так как положение касательной определяет положение орта
. Проведем через эту точку плоскость, перпендикулярную к касательной в этой точке оси. Так как положение касательной определяет положение орта ![]() системы O1X1Y1Z1, то в указанной плоскости сечения будут находиться орты
системы O1X1Y1Z1, то в указанной плоскости сечения будут находиться орты ![]() этой системы. Принимая гипотезу плоских сечений, получаем, что в рассматриваемой плоскости контур тела после искривления не изменится и определится зависимостью r=f(s,γ), где s - текущая координата по длине недеформированного тела или длина дуги искривленного тела, γ- текущий угол, характеризующий положение точки на контуре в рассматриваемом сечении; r - радиус точки, т.е. расстояние от оси до этой точки в рассматриваемой плоскости (перпендикулярной оси). Для тела вращения r=f(s)- радиус не зависит от угловой координаты; для цилиндра r=const. Орты
этой системы. Принимая гипотезу плоских сечений, получаем, что в рассматриваемой плоскости контур тела после искривления не изменится и определится зависимостью r=f(s,γ), где s - текущая координата по длине недеформированного тела или длина дуги искривленного тела, γ- текущий угол, характеризующий положение точки на контуре в рассматриваемом сечении; r - радиус точки, т.е. расстояние от оси до этой точки в рассматриваемой плоскости (перпендикулярной оси). Для тела вращения r=f(s)- радиус не зависит от угловой координаты; для цилиндра r=const. Орты ![]() могут быть приняты в качестве орт вспомогательной системы CY'1Z'1, расположенной в плоскости сечения, перпендикулярном оси в данной точке С и имеющей эту точку своим началом. При этом точка на контуре будет характеризоваться радиусом-вектором
могут быть приняты в качестве орт вспомогательной системы CY'1Z'1, расположенной в плоскости сечения, перпендикулярном оси в данной точке С и имеющей эту точку своим началом. При этом точка на контуре будет характеризоваться радиусом-вектором ![]() с модулем, определяемым по формуле, приведенной выше; начало его - точка С, компоненты y'1, z'1 - соответственно по ортам
с модулем, определяемым по формуле, приведенной выше; начало его - точка С, компоненты y'1, z'1 - соответственно по ортам ![]() .
.
Положение точки на контуре, принадлежащем поверхности искривленного тела относительно точки O будет характеризоваться радиусом - вектором ![]() , складывающимся из суммы двух векторов:
, складывающимся из суммы двух векторов:
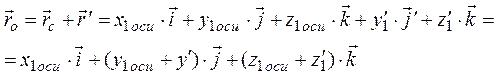
Отсюда, окончательно координаты точки на поверхности произвольного искривленного тела
![]()
причем ![]() , где r=f(s,γ). С учетом переходных формул (15):
, где r=f(s,γ). С учетом переходных формул (15):
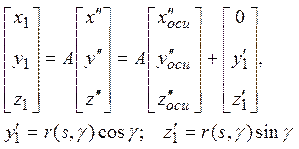
Заметим, что элементы матрицы А (см.14) всецело определяются формой искривленной оси и изменяются в зависимости от ![]() , зависящих, как следует из выражения для уравнения пространственной кривой (10), от параметра - дуги s, так что матрица А - также функция этого параметра А = А( s );
, зависящих, как следует из выражения для уравнения пространственной кривой (10), от параметра - дуги s, так что матрица А - также функция этого параметра А = А( s );
![]()
Компоненты точки поверхности, как известно, могут быть представлены в общем виде:
![]()
В нашем случае u=s - длина дуги; v= γ - угловая координата, т.к.:

Таким образом, задание искривленной поверхности сводится к заданию координат искривленной оси как функций параметра дуги и закону изменения радиуса точки в плоскостях, перпендикулярных оси.
Как следует из формул расчета аэродинамических характеристик (7) и (8), одной из главных задач является определение выражения для компонент единичного вектора нормали к поверхности. Известно соотношение
| (16) |
где ![]() …- функциональные определители:
…- функциональные определители:
![]()
Так как при описании поверхности пользуемся компонентами x",y",z" и неизвестными sи γ, необходимо получить производные типа ![]() .
.
Дифференцируя соотношения в матричном виде для x",y",z" (15) и переходя для удобства в систему X1Y1Z1, получим:
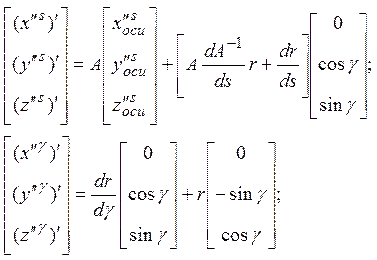
где индекс ' показывает, что величины представлены в системе X1Y1Z1.
Следует учесть, что dr/ds- это изменение радиуса тела по длине дуги s, то есть если r(s,γ)=r1(s)r2(γ), то dr/ds=r2(γ)dr1(s)/ds, причем для тела вращения r2(γ)=1 и r(s,γ)= r1(s)=r(s); для цилиндра r =const и dr/ds=0.
Из указанных формул следует, что главной задачей при определении производных является определение матрицы производных dA-1/ds=dAT/ds. Заметим, что проще рассмотреть выражение dA/ds: dA/ds=[daij/ds], тогда:
dAT/ds=[daTij/ds]=[ daij/ds]T
Рассмотрим указанное выражение с геометрической точки зрения. Так как А - матрица направляющих косинусов, определяющих положение криволинейной системы X1Y1Z1 относительно базовой (декартовой) X"Y"Z", которое изменяется вдоль дуги s, то dA/ds - это приращение (изменение) положения направляющих косинусов вдоль дуги при приращении последней на величину ds. Так как в качестве подвижных орт криволинейной системы координат были выбраны орты, связанные с касательной, нормалью и бинормалью для пространственной кривой оси (11)-(13), то для получения приращения dAможно воспользоваться известными формулами для изменения положения подвижного трехгранника, связанного с пространственной кривой (формулы Френе - Серре):
| (18) |
где K, τ- кривизна и кручение пространственной кривой;
![]() - единичные вектора касательной, нормали и бинормали.
- единичные вектора касательной, нормали и бинормали.
Gучетом определения матрицы А имеем:
| (19) |
Подставляя выражения для производных (18), получим

Следует подчеркнуть, что в указанном соотношении nx ... bz- компоненты нормали, касательной и бинормали в данной точке пространственной кривой - оси тела, выраженные в прямолинейной системе координат X"Y"Z". Итак, dА/ds выражается через компоненты матрицы А в данной точке оси, а также через значения кривизны ρk и кручения ρτ в данной точке, определяемые по формулам:

Для плоской кривой кручение τ=0, поэтому в случае выбора системы координат, ориентированной относительно плоскости изгиба, так что в последней лежат оси X"Y":
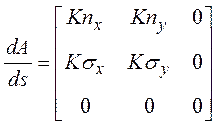
Транспонируя с учетом свойств ортогональности и разбивая на сумму двух матриц, получим окончательно для общего случая изгиба:
| (20) |
Заметим, что вектор первых членов при определении производных ![]() есть не что иное, как выражение компонент касательной к искривленной оси в рассматриваемой точке, так что с учетом обозначений:
есть не что иное, как выражение компонент касательной к искривленной оси в рассматриваемой точке, так что с учетом обозначений:
![]()
используя полученные выражения (19) и (20) для матриц А, иdА-1/dsчерез компоненты σx…nz, K, τ и проводя перемножения в соответствии со свойствами ортогональности ортонормированных базисных векторов, получим из (17)
![]()
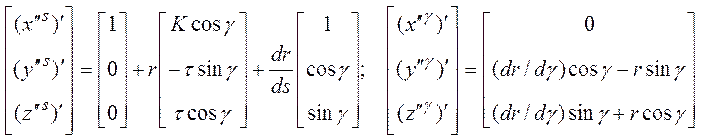
Подставляя полученные соотношения в выражения для вектора нормали (16), получим компоненты нормали к поверхности тела с произвольно искривленной осью. После перехода в систему X1Y1Z1:
| (21) |
В частном случае для цилиндра
| (22) |
Для элемента площади поверхности в точке (u,v ) известно соотношение:
![]()
В то же время для вектора нормали:
![]()
Сопоставляя, получим выражение для элементарной площади поверхности произвольного искривленного тела:
| (23) |
Для искривленного цилиндра с произвольной осью:
| (24) |
С учетом переходных формул и взаимной ориентации систем XYZ и X"Y"Z" имеем также:
| (25) |
Укажем некоторые соотношения для скоростей. Cучетом формул (3) имеем
| (26) |
где С1, С2, С3 - члены вектора С (компоненты скорости набегающего потока в местной системе координат), являющиеся функцией координаты x"или дуги s оси тела, так как А зависит от указанных величин» В этом выражении использовано представление скорости набегающего потока с помощью В - матрицы перехода от связанной к скорости системе координат
| (27) |
Компоненты вектора дополнительной скорости, возникающей при вращении тела, после раскрытия векторного произведения (5) и представления в матричной форме запишутся:
| (28) |
|
|
Последнее получено с учетом свойств транспонирования матриц.
Отметим некоторые особенности величин ΔxA, ΔyA, ΔzA. Как показали выше, координаты точки можно представить в виде суммы двух векторов. С учетом выражения для вектора относительного положения текущей точки (6) и центра вращения, компоненты которого рассматриваем, запишем
![]()
Тогда
![]()
В свою очередь вектор нормали можно представить в виде суммы двух векторов ![]() , где
, где ![]() лежит в плоскости (
лежит в плоскости (![]() ), перпендикулярной оси в данной точке по продолжению вектора
), перпендикулярной оси в данной точке по продолжению вектора ![]() ,
, ![]() направлен параллельно орту
направлен параллельно орту ![]() С учетом коллинеарности векторов
С учетом коллинеарности векторов ![]() и
и ![]() окончательно
окончательно
![]()
Для цилиндра вектор ![]() направлен по радиус-вектору
направлен по радиус-вектору ![]() , так что
, так что
![]()
Таким образом, можно рассматривать Vnωкак сумму двух составляющих - определяемой положением соответствующей точки С на оси относительно центра вращения и относительным положением точки C и точки на контуре. Компоненты вектора ![]() запишутся в виде:
запишутся в виде:
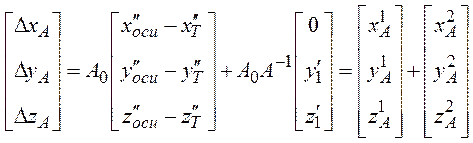
где ![]() относительные координаты оси;
относительные координаты оси; ![]() - координаты вектора
- координаты вектора ![]() , соединяющего точку на контуре и точку оси, представленные в системе XYZ.
, соединяющего точку на контуре и точку оси, представленные в системе XYZ.
Cучетом вышеизложенного
| (29) |
где D1 - вектор, определяемый исключительно положением соответствующей проекции рассматриваемой точки на ось -точки С;
D2- вектор, определяемый относительным положением точки на поверхности А и ее проекции C.
Рассмотрим первую часть - вектор D1. Перейдем от системы XYZ к системе X"Y"Z".
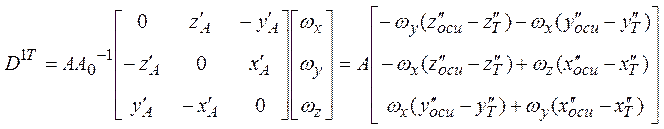
Для случая плоского искривления оси

где ε - угол наклона касательной к искривленной оси в данной точке:
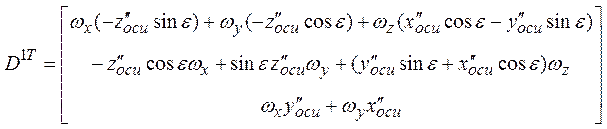
Раскрывая вторую часть, получили
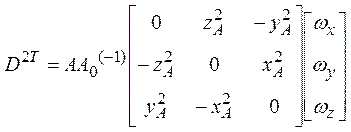
Вторую составляющую скорости можно также представить в виде:
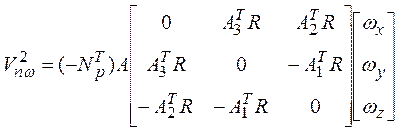
где Np - вектор-столбец компонент вектора ![]() ;
;
![]() ;
;
![]() - строки транспонированной матрицы А.
- строки транспонированной матрицы А.
Используя выражения для нормальных составляющих скоростей относительного движения Vn∞ (26) и Vnω (29), можно рассчитать в каждой точке поверхности коэффициент давления по (2). При этом предполагается, что полностью определено положение в пространстве искривленной оси: самое удобное - как функции дуги s , так что можно рассчитать члены переходной матрицы направляющих косинусов А(s), а также задано изменение радиуса тела r(s,γ).
Разбив поверхность тела на ряд элементов: например по дуге s: Δs и углу γ: Δγ, можно приближенно (численно) рассчитать интегралы (7), (8) - коэффициенты аэродинамических сил и моментов (в процессе интегрирования проверяются условия затенения и соответствующие участки либо не включаются в интеграл, либо давление в них принимается постоянным.
Выводы
Разработан эффективный матричный метод описания геометрии тел с произвольной искривленной осью, на основе которого создана общая методика расчета аэродинамических характеристик таких тел, использующая физическую гипотезу «ньютонова торможения». Указанный подход позволяет рассчитать не только аэродинамические, но и инерционные характеристики искривленных тел и может служить основой для формирования комбинированной методики деформированных тел с головной частью и оперением.
Список литературы
1. Романова И.К., Соловьев В.С. Исследование особенностей аэродинамики искривленных тел // // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2011. № 11. Режим доступа: http://technomag.edu.ru/doc/249741.html (дата обращения 14.11.2012).
2. Аэродинамика ракет. В 2 кн. / под ред. М. Хемша, Дж. Нилсена; пер. с англ. под ред. А.Д. Хонькина. М.: Мир, 1989.Кн. 1 : Введение в аэродинамику ракет. 426 с.; Кн. 2 : Методы аэродинамического расчёта. 512 с.
Публикации с ключевыми словами: пространственная кривая, искривленные тела, гипотеза «ньютонова торможения», аэродинамические характеристики, криволинейные системы координат
Публикации со словами: пространственная кривая, искривленные тела, гипотеза «ньютонова торможения», аэродинамические характеристики, криволинейные системы координат
Смотри также:
- Проектный, аэродинамический и термобаллистический анализ спускаемого аппарата класса «несущий корпус»
- Применение систем компьютерной инженерии при расчетах аэродинамических характеристик грузов, отделяемых от летательного аппарата
- Проектный анализ аэродинамических схем спускаемых аппаратов капсульной формы численным методом по ньютонианской теории обтекания
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||