научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2012
DOI: 10.7463/1212.0490457
УДК 681.3
Россия, Казанский национальный исследовательский технический университет им. А.Н. Туполева
akhatova_chulpan@mail.ru
kat_726@mail.ru
Введение
В последние десятилетия среди практических задач во многих предметных областях человеческой деятельности большое внимание стали уделять решению задач диагностики. Примерами подобных задач являются обнаружение неисправностей оборудования в технических системах, заболеваний живых организмов и всевозможных природных аномалий и т.д.
Для решения диагностических задач широкое применение получили экспертные системы, успешность применения которых основана на принципе воспроизведения знаний опытных специалистов – экспертов. Однако внесение знаний от экспертов в базу знаний представляет собой сложный процесс, тем самым, делая актуальным необходимость использования методов автоматического формирования баз знаний экспертных диагностических систем.
Некоторые исследователи, занимающиеся вопросами разработки экспертных систем, для формирования их баз знаний предлагают использовать нечеткие нейронные сети (ННС) [3, 4, 6]. Однако при их использовании возникает вопрос выбора алгоритма обучения.
В практике разработки интеллектуальных систем имеется тенденция использования гибридных моделей для решения различных практических задач. Так, применительно к обучению нечетких нейронных сетей некоторые авторы, наряду с традиционными методами оптимизации, используют генетический алгоритм [1, 2, 8]. Экспериментальные исследования, проведенные авторами, показывают, что использование данного подхода позволяет добиться лучших результатов по повышению скорости и точности решаемых задач.
Таким образом, применительно к проблеме формирования баз знаний экспертных диагностических систем актуальной задачей является разработка эффективного алгоритма обучения нечёткой нейронной сети на основе интеллектуальных методов и эффективных эвристических алгоритмов.
1 Постановка задачи исследования
Как известно, нечеткие нейронные сети представляют собой гибридные модели, сочетающие в себе достоинства нейронных сетей (возможность адаптивного самообучения) и нечетких систем (хорошая интерпретируемость получаемого с их помощью результата). При этом нечеткая нейронная сеть в результате обучения формирует систему правил, составляющих базу знаний экспертной системы.
Среди множества моделей представления знаний в настоящее время большое распространение получили правила продукций из-за их гибкости и простоты описания закономерностей предметной области. Однако большинство задач в различных областях человеческой деятельности приходится решать в условиях нечеткости, неполноты и недостоверности исходных данных. В рамках использования обычных продукционных правил решение многих задач становится затруднительным. Для их решения необходимо применять нечеткие продукции и системы нечеткого логического вывода.
Таким образом, задача настоящего исследования сводится к выбору гибкой нечетко-продукционной модели представления знаний и разработке нечеткой нейронной сети, позволяющей в результате обучения формировать базу знаний экспертной диагностической системы правилами, представленными в форме нечетких продукций.
2 Нечетко-продукционная модель представления знаний
В [5] на примере задачи планирования геолого-технических мероприятий на нефтяных месторождениях показано, что зависимость между значениями входных параметров (условиями) и назначаемым результатом может быть эффективно описана экспертом в виде следующей нечетко-продукционной модели представления знаний:
«ЕСЛИ ![]() есть
есть ![]() (
(![]() ) И
) И
![]() есть
есть ![]() (
(![]() ) И
) И
... И
![]() есть
есть ![]() (
(![]() )
)
ТО Возможно применение технологии ![]() » [
» [![]() ].
].
где ![]() – множество входных параметров правила,
– множество входных параметров правила, ![]() – множество нечетких ограничений на параметры
– множество нечетких ограничений на параметры ![]() ,
, ![]() – веса нечетких ограничений, определяющие их важность,
– веса нечетких ограничений, определяющие их важность, ![]() ∈[0, 1] – степень достоверности сформированного правила – степень уверенности эксперта в его универсальности,
∈[0, 1] – степень достоверности сформированного правила – степень уверенности эксперта в его универсальности, ![]() – технология, рекомендуемая к применению.
– технология, рекомендуемая к применению.
При этом существует алгоритм нечеткого логического вывода на правилах данной модели [5], на основе которого разработана нейронечеткая модель формирования баз знаний экспертных диагностических систем [6].
3 Нейронечеткая модель формирования баз знаний экспертных диагностических систем
Разработанная модель в виде ННС реализует алгоритм нечеткого логического вывода на нечетко-продукционной модели представления знаний [5], что определяет число слоев сети и их функциональность. Количество нейронов в слоях ННС зависит от числа входных, выходных параметров, а также числа градаций входных нейронов.
В качестве примера рассмотрим нечеткую нейронную сеть, имеющую один выход и два входа с тремя нечеткими градациями (см. рис. 1).
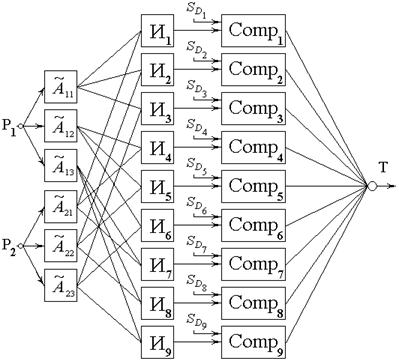
Рис. 1. Пример структуры нечеткой нейронной сети
В нулевом слое ННС содержится два Р-нейрона, выполняющих функцию распределения входных сигналов по нейронам первого слоя. В первом слое сети содержится 2*3=6 А-нейронов, которые моделируют нечеткие условия вида «Р есть ![]() ». Выход А-нейронов равен значениям функций принадлежности
». Выход А-нейронов равен значениям функций принадлежности ![]() (степень срабатывания условий) при соответствующих значениях входных нейронов. Второй слой содержит 32=9 И-нейронов, задающих нечеткие продукции в виде «ЕСЛИ
(степень срабатывания условий) при соответствующих значениях входных нейронов. Второй слой содержит 32=9 И-нейронов, задающих нечеткие продукции в виде «ЕСЛИ ![]() есть
есть ![]() И
И ![]() есть
есть ![]() ТО
ТО ![]() ». Выход И-нейронов определяет оценку срабатывания соответствующего правила
». Выход И-нейронов определяет оценку срабатывания соответствующего правила ![]() . Третий слой сети состоит из девяти Comp-нейронов, на выходе которых рассчитываются комплексные оценки срабатывания правил, равные произведению значений соответствующих оценок доверия к принятому решению
. Третий слой сети состоит из девяти Comp-нейронов, на выходе которых рассчитываются комплексные оценки срабатывания правил, равные произведению значений соответствующих оценок доверия к принятому решению ![]() на оценки
на оценки ![]() . Веса связи Comp-нейронов с выходом ННС определяют степени достоверности сформированных правил
. Веса связи Comp-нейронов с выходом ННС определяют степени достоверности сформированных правил ![]() . Произведения выходов Comp-нейронов на их веса образуют общий коэффициент достоверности решений. В четвертом слое содержится Т-нейрон, на выходе которого вычисляются взвешенные нормированные оценки достоверности принимаемого решения.
. Произведения выходов Comp-нейронов на их веса образуют общий коэффициент достоверности решений. В четвертом слое содержится Т-нейрон, на выходе которого вычисляются взвешенные нормированные оценки достоверности принимаемого решения.
Для получения системы правил, формирующих базу знаний экспертной диагностической системы, необходимо произвести обучение нечеткой нейронной сети, которое заключается в настройке значений соответствующих параметров ее функций принадлежности ![]() .
.
4 Гибридный алгоритм обучения нечеткой нейронной сети
Для обучения ННС разработан гибридный алгоритм, сочетающий в себе достоинства генетических алгоритмов с принципами градиентного метода обучения. Рассмотрим этапы работы гибридного алгоритма обучения ННС.
1. Задаются начальное значение адаптивного шага обучения 𝛼 (0 < 𝛼 < 1), желаемая ошибка выхода нейронной сети ![]() , а также минимальный порог изменения ошибки при обучении
, а также минимальный порог изменения ошибки при обучении ![]() .
.
2. На вход сети подаются i-е образы из обучающей выборки, для каждого из которых:
· производится фаза прямого распространения сигнала по нейронной сети, определяется взвешенная активность выходного нейрона (значение выхода ![]() );
);
· вычисляется среднеквадратичная ошибка выхода нейронной сети для i-го входного образа 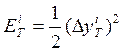 , где
, где ![]() – абсолютная ошибка выхода;
– абсолютная ошибка выхода; ![]() – требуемое значение выхода;
– требуемое значение выхода;
· для минимизации ошибки ![]() последовательно настраиваются выходы Comp-нейронов
последовательно настраиваются выходы Comp-нейронов ![]() на основе генетического алгоритма GAMT (GeneticAlgorithmforMinimizedT-error);
на основе генетического алгоритма GAMT (GeneticAlgorithmforMinimizedT-error);
· вычисляются требуемые значения выходов И-нейронов 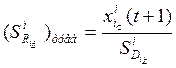 , где t – момент времени;
, где t – момент времени;
· рассчитываются среднеквадратичные ошибки выходов И-нейронов 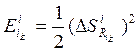 , где
, где ![]() – абсолютная ошибка выхода,
– абсолютная ошибка выхода, ![]() – требуемое значение выхода;
– требуемое значение выхода;
· для минимизации ошибки ![]() последовательно модифицируются параметры функций принадлежности соответствующих А-нейронов на основе генетического алгоритма GAMИ (GeneticAlgorithmforMinimized И-error).
последовательно модифицируются параметры функций принадлежности соответствующих А-нейронов на основе генетического алгоритма GAMИ (GeneticAlgorithmforMinimized И-error).
3. Вычисляется среднее значение ошибки выхода для всех входных образов: 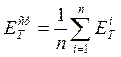 .
.
4. Рассчитывается изменение ошибки выхода: ![]() .
.
5. Если 0≤![]() ≤
≤![]() , то процесс обучения заканчивается.
, то процесс обучения заканчивается.
6. Если ![]() , то происходит переход к шагу 7 алгоритма, иначе процесс обучения нечеткой нейронной сети заканчивается.
, то происходит переход к шагу 7 алгоритма, иначе процесс обучения нечеткой нейронной сети заканчивается.
7. Проверяется условие не возрастания ошибки выхода нейронной сети: если ![]() <0, то уменьшается адаптивный шаг обучения и происходит переход ко 2-му шагу алгоритма.
<0, то уменьшается адаптивный шаг обучения и происходит переход ко 2-му шагу алгоритма.
На рисунке 2 представлена блок-схема данного алгоритма.
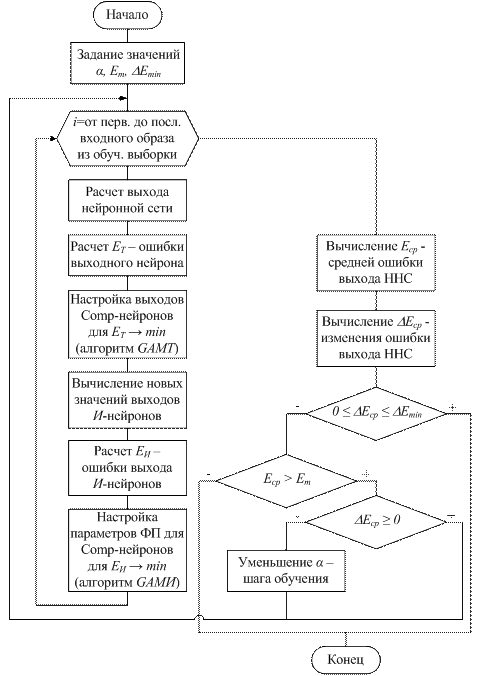
Рис. 2. Блок-схема алгоритма обучения нечеткой нейронной сети
Данный алгоритм функционирует до тех пор, пока средняя ошибка выхода нейронной сети не станет меньше заданной (![]() ) либо изменение ошибки выхода
) либо изменение ошибки выхода ![]() не будет превышать минимально допустимый уровень
не будет превышать минимально допустимый уровень ![]() .
.
В рамках соответствующих генетических алгоритмов происходит настройка выходов Comp-нейронов, а также искомых значений параметров соответствующих функций принадлежности А-нейронов. Рассмотрим этапы работы данных алгоритмов.
5 Этапы работы генетических алгоритмов
Общим в работе каждого из алгоритмов является то, что они соответствуют принципам работы классического генетического алгоритма [7]. Таким образом, для практического применения алгоритмов необходимо задать способ кодирования и декодирования параметров задачи, определить правило создания начальной популяции хромосом, ввести оценку приспособленности хромосом в популяции, разработать правила селекции хромосом, применения генетических операторов скрещивания и мутации, а также формирования новой популяции.
Кодирование и декодирование параметров задачи
Рассмотрим способ кодирования параметров задачи для генетического алгоритма GAMИ. Как было сказано выше, его работа заключается в настройке соответствующих параметров функций принадлежности ННС, которые задаются некоторой параметризованной функцией формы (треугольной, трапецеидальной, гауссовой и др.) с вектором параметров ![]() . Так, для треугольной функции принадлежности
. Так, для треугольной функции принадлежности ![]() , где
, где ![]() – левое основание,
– левое основание, ![]() – центр (мода),
– центр (мода), ![]() – правое основание.
– правое основание.
Настройка параметров ![]() функций принадлежности осуществляется в окрестности ∆=[
функций принадлежности осуществляется в окрестности ∆=[![]() ], ширина которой определяется индивидуально для каждого параметра и может составлять до 30 % ширины ее основания.
], ширина которой определяется индивидуально для каждого параметра и может составлять до 30 % ширины ее основания.
Разобьем данную окрестность на 2n интервалов, где n – целое число, например, 10. Тогда параметр ![]() сможет принимать одно из 210 значений, которые будут кодироваться хромосомой {
сможет принимать одно из 210 значений, которые будут кодироваться хромосомой {![]() } длиной 10 бит. При этом хромосома, состоящая из нулей, будет соответствовать значению параметра
} длиной 10 бит. При этом хромосома, состоящая из нулей, будет соответствовать значению параметра ![]() , а состоящая из единиц – значению
, а состоящая из единиц – значению ![]() . Таким образом, мощность хромосомного набора для каждого параметра
. Таким образом, мощность хромосомного набора для каждого параметра ![]() функции принадлежности равна числу 2n.
функции принадлежности равна числу 2n.
Во время работы алгоритма GAMT происходит настройка выходов Comp-нейронов ![]() , область значений которых постоянна и равна [0, 1]. Способ разбиения данного отрезка и кодирование значений выходов Comp-нейронов аналогичны алгоритму GAMИ. При этом мощность хромосомного набора для каждого параметра
, область значений которых постоянна и равна [0, 1]. Способ разбиения данного отрезка и кодирование значений выходов Comp-нейронов аналогичны алгоритму GAMИ. При этом мощность хромосомного набора для каждого параметра ![]() также равна числу 2n.
также равна числу 2n.
Во время обучения нечеткой нейронной сети возникает необходимость перехода от хромосомного набора к десятичным значениям параметров. Для этого необходимо выполнить процедуру декодирования, являющуюся инверсной по отношению к операции кодирования хромосом.
Создание начальной популяции хромосом
Функционирование генетических алгоритмов начинается с создания начальных популяций хромосом для всех параметров ННС, участвующих в обучении. При задании значения числа n мощность хромосомного набора для любого параметра постоянна и равна 2n, где n – длина хромосомы. Объем начальной популяции хромосом N рекомендуется выбирать на порядок меньше числа 2n. Однако при малых значениях n (n<10) данный объем должен быть сравним с числом ![]() . Так, например, при n=10 для создания начальной популяции случайным образом выбираются N=100 хромосом chi (i=1..N) из общего хромосомного набора мощностью 1024.
. Так, например, при n=10 для создания начальной популяции случайным образом выбираются N=100 хромосом chi (i=1..N) из общего хромосомного набора мощностью 1024.
Следует отметить, что значения n<10 выбирать не рекомендуется. Это приводит к малой вариабельности параметров, что в дальнейшем может негативно отразиться на результатах обучения нечеткой нейронной сети.
Оценка приспособленности хромосом в популяции
Когда соответствующие параметры ННС закодированы и сформированы начальные популяции хромосом, необходимо оценить приспособленность каждой хромосомы chi в популяции.
В генетическом алгоритме GAMT в роли функции приспособленности выступает среднеквадратичная ошибка выхода нейронной сети ![]() . Соответственно, в алгоритме GAMИ функцией приспособленности является ошибка выхода И-нейрона
. Соответственно, в алгоритме GAMИ функцией приспособленности является ошибка выхода И-нейрона ![]() .
.
Для оценки приспособленности хромосом chi производится расчет значений соответствующих функций приспособленности, на вход которых подаются декодированные значения хромосом. При этом каждой хромосоме chi из общего хромосомного набора ставится в соответствие величина ее приспособленности E(chi).
Селекция хромосом
Селекция хромосом заключается в выборе по рассчитанным значениям функции приспособленности тех хромосом, которые будут участвовать в создании особей следующего поколения. Такой выбор производится согласно принципу естественного отбора, по которому наибольшие шансы на участие в создании потомков имеют хромосомы с наименьшими значениями функции приспособленности (исходя из требования минимизации среднеквадратичной ошибки).
Оператор селекции реализуется на основе метода рулетки [9]. Для каждой хромосомы текущей популяции формируется сектор на колесе рулетки, площадь которого пропорциональна значению инверсной вероятности селекции данной хромосомы pi=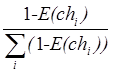 (см. рис. 3).
(см. рис. 3).
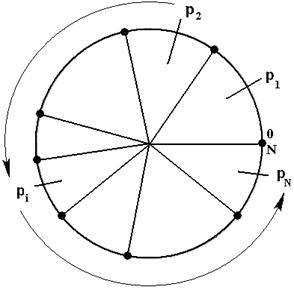
Рис. 3. Колесо рулетки для селекции хромосом
Розыгрыш с помощью колеса рулетки сводится к случайному выбору числа из интервала [0, N], указывающего на сектор колеса, которому соответствует конкретная хромосома. Таким способом из текущей популяции выбираются два кандидата-родителя, к которым в дальнейшем применяются генетические операторы для порождения потомков.
Применение генетических операторов
Основными операторами описываемых генетических алгоритмов являются операторы скрещивания и мутации, которые применяются к хромосомному набору соответствующих параметров нечеткой нейронной сети. Рассмотрим пример работы оператора скрещивания (см. табл. 1).
Табл. 1. Пример работы оператора скрещивания
Позиции генов Хромосомы | 1 | … | i | i+1 | … | n |
X | α1 | … | αi | αi+1 | … | αn |
Y | β1 | … | βi | βi+1 | … | βn |
|
|
| ↓ |
|
|
|
Z | α1 | … | αi | βi+1 | … | βn |
Q | β1 | … | βi | αi+1 | … | αn |
Здесь X и Y – исходные решения (родители), Z, Q – новые решения.
Как видно из таблицы, в исходных хромосомах случайным образом выбирается точка скрещивания (в данном случае в i-й позиции хромосом), после чего происходит обмен противоположными частями родителей. Так происходит рождение новых потомков. Отметим, что процесс скрещивания носит случайный характер и производится с вероятностью рс∈[0.5, 1].
Оператор мутации, применяемый к потомкам после скрещивания, также производится случайно с вероятностью рм∈[0, 0.05]. Сам процесс мутации заключается в инверсии одного из битов строки дочерних хромосом, выбираемого по равномерному закону.
Таким образом, в результате выполнения генетических операторов исходная популяция хромосом за счет порожденных новых потомков увеличилась на 2 члена. Однако размер следующего поколения хромосом должен оставаться постоянным. Рассмотрим, каким образом решается задача сокращения размерности хромосомного набора на этапе формирования новой популяции.
Формирование новой популяции
Для сокращения размера популяции до исходного числа особей применяется оператор редукции. Для этого оценивается приспособленность каждой хромосомы, после чего из популяции исключаются две хромосомы с максимальным значением целевой функции.
Таким образом, с каждым циклом работы генетических алгоритмов в популяциях остаются только наиболее приспособленные хромосомы, уменьшающие значение среднеквадратичной ошибки выхода нейронной сети. Это значит, что после останова работы алгоритмов получим обученную нечеткую нейронную сеть с функциями принадлежности и правилами, позволяющими с заданной точностью аппроксимировать данные из обучающей выборки.
6 Апробация нейронечеткой системы и анализ эффективности алгоритмов обучения нечеткой нейронной сети
На базе описанной модели формирования баз знаний экспертных диагностических систем реализована нейронечеткая система. В качестве примера ее практического использования рассмотрим процесс анализа медицинских данных. Пусть необходимо выявить зависимость между временными параметрами пациента и риском возникновения у него заболевания.
В качестве входов нейронной сети примем параметры «возраст пациента», «стаж заболевания» и «стаж физических нагрузок», а в качестве выхода – «протрузия межпозвонкового диска». В результате обучения нечеткой нейронной сети получим правила следующего вида:
ЕСЛИ «Возраст пациента»=«средний» (w=0,47) И
«Стаж заболевания»=«большой» (w=0,59) И
«Стаж физических нагрузок»=«большой» (w=0,61)
ТО «Возможно наличие протрузии диска» (CF=0,63).
Особенности формирования базы знаний с использованием нечеткой нейронной сети изучались при разработке экспертной системы диагностики клинических проявлений остеохондроза поясничного отдела позвоночника [9].
Для получения системы правил и их параметров измерено более 500000 значений признаков течения поясничного остеохондроза по 822 признакам. В результате применения нейронечеткой системы на более чем 100 обучающих выборках получено более 500 правил, значимость которых подтверждена экспертами – специалистами-вертеброневрологами.
Результаты проведенного исследования подтвердили возможность и эффективность применения нейронечеткой системы для диагностического процесса в вертеброневрологии.
Для анализа эффективности алгоритмов обучения ННС было произведено сравнение результатов применения гибридного алгоритма обучения ННС с результатами, полученными в предыдущих исследованиях на базе алгоритма обратного распространения ошибки [6] и генетического алгоритма [7]. Был проведен ряд численно-параметрических исследований сравнения эффективности работы алгоритмов по критериям «скорость обучения» и «точность аппроксимации» на множестве обучающих выборок (см. табл. 2).
Табл. 2. Результаты сравнения эффективности алгоритмов
Наименование алгоритма | Значение параметра | Оцениваемые параметры | ||||
Значение выхода | Ошибка выхода | Время обучения | Число эпох | |||
Обратного распространения ошибки | лучшее | 0,7 | 0,05 | 00:01:48 | 96247 | |
среднее | 0,63 | 0,07 | 00:02:11 | 114247 | ||
худшее | 0,3 | 0,25 | 00:10:27 | 547195 | ||
Генетический алгоритм | лучшее | 0,62 | 0,07 | 00:00:58 | 517 | |
среднее | 0,57 | 0,09 | 00:01:25 | 736 | ||
худшее | 0,43 | 0,16 | 00:02:46 | 1461 | ||
Гибридный алгоритм | лучшее | 0,83 | 0,01 | 00:00:16 | 93 | |
среднее | 0,75 | 0,03 | 00:00:42 | 248 | ||
худшее | 0,59 | 0,08 | 00:01:07 | 371 | ||
Как видно из таблицы, результаты работы гибридного алгоритма обучения нечёткой нейронной сети по всем критериям лучше соответствующих результатов работы других алгоритмов. В некоторых случаях эффективность гибридного алгоритма была сравнима с эффективностью простого генетического алгоритма. При этом эффективность алгоритма обратного распространения ошибки оказалось самой низкой.
Заключение
Практическое значение нейронечеткой модели заключается в возможности эффективного формирования баз знаний экспертных диагностических систем. Обученная нейронная сеть является адаптивной системой нечеткого логического вывода. Она может использоваться как инструмент эксперта в составе мягкой экспертной диагностической системы и позволяет заменить (или дополнить) эвристический процесс построения базы знаний на процесс автоматизированного ее формирования, извлекая продукционные закономерности из статистических выборок данных.
Таким образом, предложенная в работе нейронечеткая система с гибридным алгоритмом обучения вносит определенный вклад в развитие технологий интеллектуального анализа данных и формирования баз знаний экспертных диагностических систем.
Список литературы
1. Arotaritei D. Genetic Algorithm for Fuzzy Neural Networks using Locally Crossover // International Journal of Computers Communications & Control. 2011. Vol. 6, no. 1. P. 8-20.
2. Banakar Ahmad, Mohammad Fazle Azeem. Wavelet Neuro-Fuzzy Model With Hybrid Learning Algorithm Of Gradient Descent And Genetic Algorithm // International Journal of Wavelets Multiresolution And Information Processing. 2011. Vol. 9, no. 2. P. 333-359. DOI:10.1142/S021969131100402X
3. Klawonn F., Nauck D., Kruse R. Generation Rules from Data by Fuzzy and Neuro-Fuzzy Methods // Proc. of the Third German GI-Workshop “Fuzzy-Neuro-Systeme’95”, Darmstadt, Germany, 15-17 November, 1995.
4. Глова В.И., Аникин И.В., Катасёв А.С., Подольская М.А. Формирование базы знаний медицинской диагностической экспертной системы на основе нечеткой нейронной сети // Исследования по информатике. Вып. 12. Казань: Отечество, 2007. С. 31-46.
5. Глова В.И., Аникин И.В., Шагиахметов М.Р. Методы многокритериального принятия решений в условиях неопределённости в задачах нефтедобычи. Казань: Казан. гос. техн. ун-т, 2004. 31 с. (Препринт / КГТУ; № 04П2).
6. Катасёв А.С. Нейронечеткая модель и программный комплекс формирования баз знаний экспертных систем : автореф. дисс. … канд. техн. наук. Казань, 2006. 20 с.
7. Катасёв А.С. Ахатова Ч.Ф. Нейронечеткая модель формирования баз знаний экспертных систем с генетическим алгоритмом обучения // Проблемы управления и моделирования в сложных системах: труды XII Межд. конференции. Самара: Самарский научный центр РАН, 2010. С. 615-621.
8. Лавыгина А.В., Ходашинский И.А. Гибридный алгоритм настройки параметров нечетких моделей // Двенадцатая национальная конференция по искусственному интеллекту с международным участием КИИ-2010 (Россия, Тверь, 20-24 сентября 2010 г.) : труды. Т. 4. М.: Физматлит, 2010. С. 112-115.
9. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы : пер. с польск. И.Д. Рудинского. М.: Горячая линия – Телеком, 2006. 452 с.
Публикации с ключевыми словами: экспертная система, нечеткая нейронная сеть, база знаний, модель представления знаний, задача диагностики
Публикации со словами: экспертная система, нечеткая нейронная сеть, база знаний, модель представления знаний, задача диагностики
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



