научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2012
DOI: 10.7463/1112.0486675
УДК 629.113
Россия, МГТУ им. Н.Э. Баумана
zuzvalery@rambler.ru
Пассивная безопасность колесных машин в настоящее время представляет собой одну из наиболее важных задач, которую приходится решать при проектировании новых транспортных средств. И, в то же время, эта задача очень сложная и трудоемкая, поскольку связана с ударом и, как следствие, является сильно нелинейной с большими деформациями, напряжениями и ускорениями. Применительно к кузовам легковых автомобилей и кабинам грузовых автомобилей одним из наиболее сложных состояний является удар в передние стойки и бампер. При этом конструкция испытывает контакт, потерю устойчивости, смятие, изгиб, появление пластических шарниров и др. Решение таких задач ведется методом конечных элементов (МКЭ) и даже на современных ЭВМ может длиться много часов.
Известно, что основную долю энергии удара воспринимают элементы каркасного типа кабин и кузовов [1]. Кроме того, они представляют собой тонкостенные конструкции относительно малого поперечного сечения, нередко переменного по длине, и часто имеют изогнутую форму, могут иметь отверстия, накладки и соединяются обычно точечной сваркой (рис. 1, 9, 20). Моделирование таких конструкций при использовании генераторов сетки конечных элементов очень часто затруднено (из-за указанных особенностей конструкции, а также из-за малых радиусов скругления). Поэтому в этой статье основное внимание уделено разработке конечно-элементных моделей (КЭМ) именно каркасных элементов. Поскольку решаемые задачи сильно нелинейные, то нередко длятся несколько часов, поэтому актуальной проблемой является разработка рациональных КЭМ конструкций, которые позволят получать решения с приемлемой погрешностью и продолжительностью.
Целью данной работы является разработка рациональных КЭМ тонкостенных каркасных элементов кузовов и кабин автомобилей с учетом особенностей конструкции, исследование поведения их при ударе, осуществляемом в соответствии с существующими стандартами пассивной безопасности, оценка полученных результатов расчетов с позиций погрешностей и трудозатрат на разработку и решение с помощью программных комплексов, реализующих МКЭ (ANSYS и LS-DYNA).
В настоящее время каждый автомобиль должен соответствовать целому ряду стандартов пассивной безопасности, основными из которых являются правила единой экономической комиссии при Организации Объединенных Наций (ЕЭК ООН), а также правила Euro NCAP (для легковых автомобилей) и отечественные стандарты, действующие на территории России. Поэтому в качестве расчетных нагрузочных использовались режимы, соответствующие этим стандартам и, прежде всего, удар маятником по стойкам – как один из наиболее опасных. Для оценки погрешностей результатов расчетов использовалось сравнение с экспериментальными данными.
Исследование поведения передней стойки легкового автомобиля при ударе. В качестве объекта исследования была выбрана оригинальные передние стойки автомобиля Форд CD (рис. 1).

Рис. 1. Фрагмент стойки для испытаний

Рис. 2. Схема нагружения стойки при испытаниях по правилам EuroNCAP
Стойки имеют изогнутую форму, радиусы скруглений разной величины, на внутренней части многочисленные отверстия и выштамповки, они сварены точечной сваркой из восьми штампованных стальных листов толщиной в диапазоне 0,75-1,0 мм. Ударная нагрузка прикладывается к передней части стойки, ее скорость V= 15,56-17,78 м/с (56-64 км/ч), что соответствует правилам Euro NCAP.
Картины деформированных состояний экспериментальной модели стойки представлены на рис. 3 [2].



Рис. 3. Деформированное состояние стойки после удара (эксперимент)

Рис. 4. Оболочечные КЭМ стойки: а – «низший уровень»; б – «средний уровень»; в – «высший уровень»
На рис. 4 представлены разработанные оболочечные КЭМ стойки: а – «низший уровень» (число узлов 1487, число элементов 1412, размер элементов 35 мм); б – «средний уровень» (число узлов 6438, число элементов 6331, размер элементов 7 мм), в – «высший уровень» (число узлов 23942, число элементов 23655, размер элементов 3,5 мм). КЭМ разрабатывались с учетом решения большого числа модельных задач (в том числе [3, 4]), а также мирового опыта. Они несколько идеализированы, например, малые радиусы скруглений не моделировались.
На рис. 5 и 6 показаны картины деформированных состояний для КЭМ стойки разной сложности («низший», «средний» и «высший уровень») и характер изменения зоны пластических деформаций в зависимости от уровня сетки КЭМ.

Рис.5. Картина деформированного состояния (перемещения в мм) КЭМ «высшего уровня» стойки и зон пластических деформаций в ней

Рис.6. Картины деформированных состояний КЭМ стойки: а – «низший уровень»; б – «средний уровень»; в – «высший уровень»


На рис. 7, 8. показаны графики изменения ударной нагрузки Рр в зависимости от перемещений S при скорости 64-56 км/ч, полученные по результатам расчёта КЭМ разного уровня и экспериментально. Из графиков видно, что максимальное значение ударной нагрузки наблюдается в начальный момент пластической деформации, после чего происходит изменение геометрической формы сечения и снижение величины ударной нагрузки Рр.
Площадь под кривой Pp(S) представляет собой поглощенную энергию Ек конструкции:![]() .
.
Результаты расчетов и погрешности решения ударной задачи для стойки с использованием оболочечных КЭМ различного типа представлены в таблице 1.
Таблица 1.
Результаты решения ударной задачи для стойки с использованием
оболочечных КЭМ различного типа (LS DYNA)
Скорость [км/ч] | Модель | Число узлов | Число элеметов | Размер элементов [мм] | Поглощённая энергия | Погрешность | |
Экспериментальная | Расчетная (LS DYNA) | ||||||
64 | а- низший уровень | 1487 | 1412 | 35 | 8190,05 | 13351,64 | 63% |
б- средний уровень | 6438 | 6331 | 7 | 9422,32 | 15% | ||
в- высший уровень | 23942 | 23655 | 3,5 | 8436,76 | 3% | ||
56 | а- низший уровень | 1487 | 1412 | 35 | 12508,14 | 53% | |
б- средний уровень | 6438 | 6331 | 7 | 8858,1 | 8% | ||
в- высший уровень | 23942 | 23655 | 3,5 | 7985,71 | 2% | ||
Анализ полученных результатов позволяет сделать вывод, что оболочечная КЭМ высшего уровня (число узлов 23942, число элементов 23655, размер элементов 3,5 мм) обеспечивает получение минимальной погрешности результатов по сравнению с экспериментальными данными. Поэтому она будет использоваться как основная на последующих этапах, а модель среднего уровня может использоваться для предварительных и многовариантных расчетов.
Исследование поведения бампера легкового автомобиля при ударе. Бампер — энергопоглощающее устройство автомобиля (на случай лёгкого удара) в виде бруса, расположенного как спереди так и сзади. Эта задача представляет интерес в связи с тем, что согласно экспериментальным данным бампер при ударе может испытывать сложный нелинейный характер поведения, имеющего много общего с поведением каркасных элементов кабин и кузовов: потерю устойчивости, локальное смятие и образование пластических шарниров, а также продольное смятие труб крепления к кузову. При составлении КЭМ разного уровня также учитывались ранее проведенные исследования [7, 8]. В качестве объекта исследований был выбран бампер из алюминиевого сплава (рис. 9). Свойства материала представлены на рис. 10.



Рис. 9. Основные сечения и размеры бампера: (а) сечение бампера AA повёрнутое на 90 °; (б) сечение ВВ , (с) вид на крепление (фланец) детали

Рис. 10. Характеристики используемого алюминиевого сплава AA7003-T79: 1- полученные экспериментально; 2- расчётные (![]() -напряжение,
-напряжение, ![]() -деформация)
-деформация)
Схема ударного нагружения маятником и результаты эксперимента представлены на рис. 11 и 12 [5].

Рис. 11. Схема нагружения бампера



Рис. 12. Картины деформированных состояний бампера по времени удара
Моделировался фронтальный удар с частичным перекрытием (косо-фронтальный удар «маятник – бампер») в соответствии с требованиями ЕЭК ООН (начальная скорость V=10 м/с, соответствующая необходимой кинетической энергии в момент удара 39,7 кДж, рис. 9, 12).
Для оценки степени восприятия нагрузок каркасом бампера и картины распределения зон пластических деформаций были созданы КЭМ бампера разной степени сложности (рис. 13).

Рис. 13. Оболочечные КЭМ бампера: а – «низший уровень»; б – «средний уровень»; в – «высший уровень»
На рис. 13 показаны оболочечные КЭМ модели бампера: а – «низший уровень» (число узлов 2400, число конечных элементов 1883, размер элементов 40 мм); б – «средний уровень» (число узлов 13475, число элементов 11636, размер элементов 20 мм), в – «высший уровень» (число узлов 26593, число элементов 25071, размер элементов 7 мм).
Картины деформированных состояний, полученные экспериментально и расчетным путем для разных зон («а», «б», «в») показаны на рис. 14. Их сравнение свидетельствует о высокой степени адекватности.


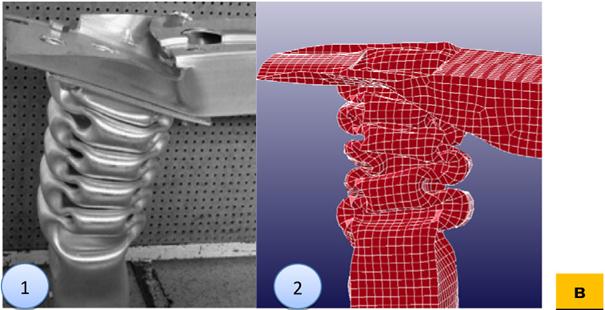
Рис. 14. Картина деформированного состояния бампера: 1-эксперимент; 2- расчёт
На рис. 15-19 представлены графики изменений параметров, полученные экспериментально и расчетным путем для КЭМ разного уровня.
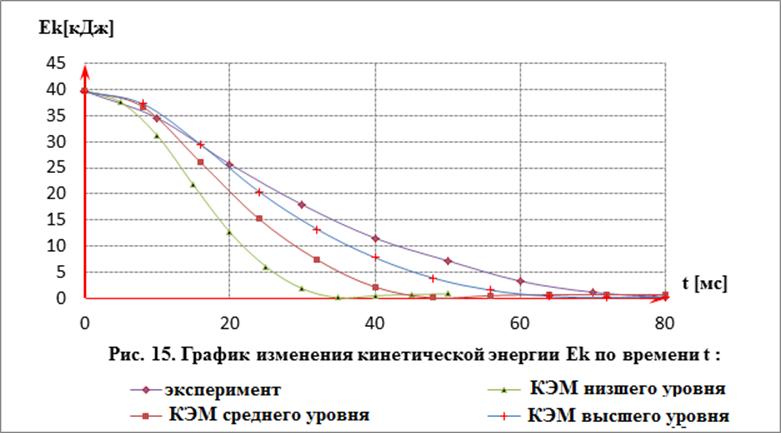


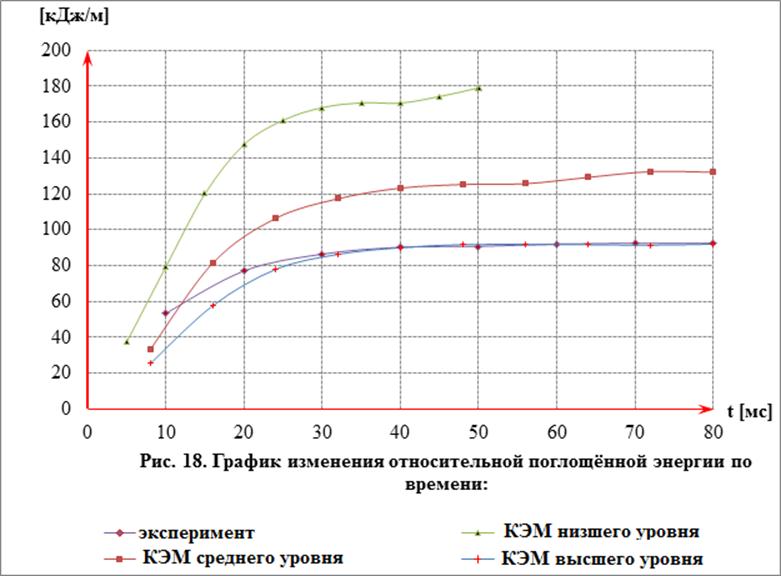

Погрешности решений и основные характеристики сетки КЭМ представлены в таблице 2.
Таблица 2.
Результаты решения ударной задачи для бампера с использованием оболочечных КЭМ различного типа (LS DYNA)
Модель | Число узлов | Число элементов | Размер элемента, мм | поглощённая энергия [кДж] | Относительная погрешность по поглощённой энергии% | перемещения S [мм] | Относительная погрешность по S, % | Относительная поглощённая энергия [кДж/м] | Относительная погрешность по относительной поглощенной энергии % | ||
Эксперимент | Расчет МКЭ (LSDYNA) | Эксперимент | Расчет МКЭ (LSDYNA) | ||||||||
а- КЭМ низшего уровня | 2400 | 1883 | 40 | 39,70 | 39,64 | 0,15 | 431,25 | 232,10 | 46,18 | 179,16 | 46,33 |
б- КЭМ среднего уровня | 13475 | 11636 | 20 | 39,70 | 39,69 | 0,03 | 431,25 | 317,00 | 26,49 | 132,07 | 26,52 |
в- КЭМ высшего уровня | 26593 | 25071 | 7 | 39,70 | 39,56 | 0,35 | 431,25 | 432,50 | 0,29 | 91,93 | 0,64 |
Исследование поведения каркаса грузового автомобиля при ударе. В качестве объекта была выбрана кабина грузового автомобиля Scania (рис. 20), имеющая достаточно типичную и распространённую компоновку и конструкцию, для которой также имеются результаты экспериментальных исследований.
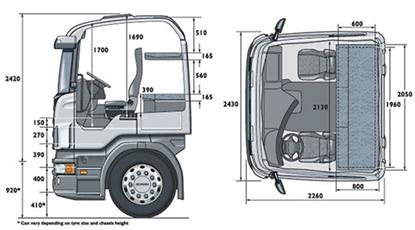
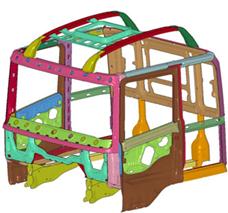
Рис. 20. Кабина ScaniaCR19 бескапотной компоновки с одним или двумя спальными местами
Моделируется процесс удара маятником по стойкам в передней части кабины по методике (правилам) Швеции VVFS 2003 № 29 методом конечных элементов в программном комплексе LS-DYNA (рис. 21).
Впроцессе моделирования динамического удара цилиндрическому маятнику задавалась начальная скорость V=7,668 м/с, соответствующая необходимой кинетической энергии в момент удара, равной 29,4 [кДж] (рис. 21) [6-8].
Для оценки погрешностей моделирования были созданы КЭМ каркаса разной степени сложности (рис. 22).

Рис. 21. Расчётная схема моделирования ударом маятника в угол крыши



Рис. 22. Оболочечные КЭМ каркаса кабины: а – «низший уровень»; б – «средний уровень»; в – «высший уровень»
На рис. 22 показаны оболочечные КЭМ каркаса кабины: а – «низший уровень» (число узлов 18313, число конечных элементов 18678, размер элементов 11 мм); б – «средний уровень» (число узлов 36972, число элементов 37352, размер элементов 6 мм), в – «высший уровень» (число узлов 100383, число элементов 100733, размер элементов 3 мм). Результаты расчётов модели каркаса кабины при ударе (Правила Швеции VVFS 2003 № 29) показаны на рис. 23-28. Продолжительность решений (5-ти ядерный процессор) – 5, 9 и 14 часов соответственно.

Рис. 23. Картина деформированного состояния КЭМ каркаса кабины

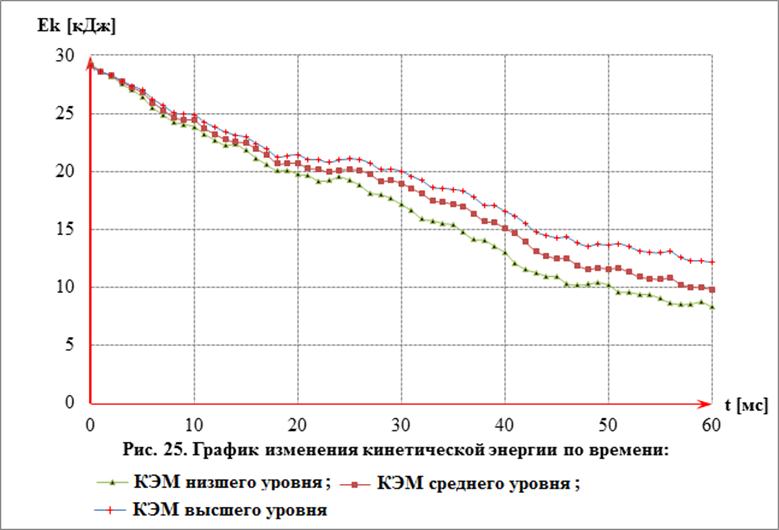


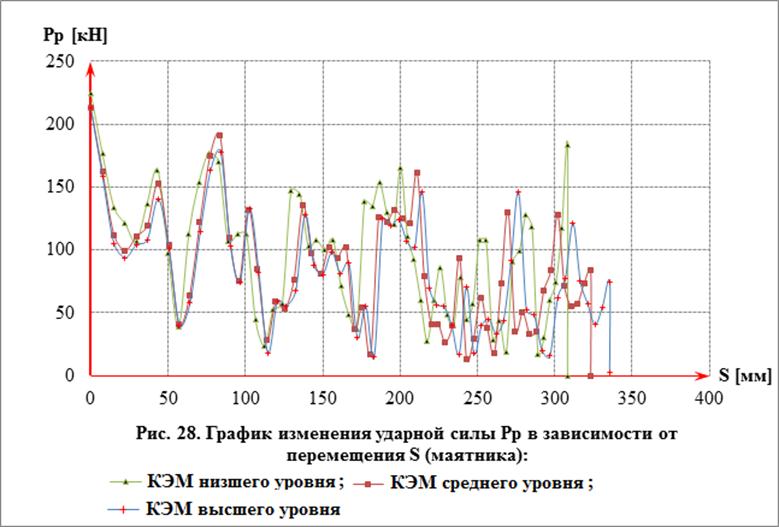
Произведенные расчёты каркаса кабины дали всю необходимую информацию о процессе аварийного нагружения, необходимого для оценки пассивной безопасности кабин грузовых автомобилей, а именно: о характере деформирования, о зонах пластических деформаций, о характере изменения скорости и перемещения ударного элемента и изменения ударной нагрузки, необходимых для определения относительной поглощённой энергии конструкции и др.
На основе проведённых исследований можно сделать следующее заключение:
1. Для анализа поведения тонкостенных каркасных элементов кузовов и кабин автомобилей при исследованиях пассивной безопасности необходимо использовать КЭМ оболочечного типа высшего уровня (размер элементов 3-5 мм, средняя погрешность 3-5% по сравнению с экспериментом).
2. Для предварительных и многовариантных расчётов можно использовать модели среднего уровня (размер элементов 6-10 мм, средняя погрешность 10-20% по сравнению с экспериментом). По значениям трудозатрат на ее создание и решение задачи и по погрешностям результатов такие модели можем считать рациональными.
СПИСОК ЛИТЕРАТУРЫ
1. Lönn D., Öman M., Nilsson L., Simonsson K. Finite element based robustness study of a truck cab subjected to impact loading. International Journal of Crashworthiness. 2009. Vol. 14, no. 2. P. 111–124. DOI:10.1080/13588260802412992
2. Hanssen G., Stöbener K., Rausch G., Langseth M., Keller H. Optimization of energy absorption of an A-pillar by metal foam insert, International Journal of Crashworthiness. 2006. Vol. 11, no. 3. P. 231-242. DOI:10.1533/ijcr.2005.0396
3. Зузов И.В. Моделирование продольного смятия передних лонжеронов кузова легкового автомобиля с учетом инициаторов деформаций // Известия высших учебных заведений. Машиностроение. 2011. № 1. С. 34-37.
4. Зузов И.В., Зузов В.Н. Моделирование продольного смятия передних лонжеронов кузова легкового автомобиля с учетом наполнителей и инициаторов деформаций // Известия высших учебных заведений. Машиностроение. 2012. № 2. С. 42-45.
5. Satyanarayana Kokkula. Bumper beam-longitudinal system subjected to offset impact loading an experimental and numerical study. PhD Thesis. Norwegian University of Science and Technology, 2005. 288 p.
6. Ulug C.D. Effect of strain history on simulation of crashworthiness of vehicles. Master Thesis. Department of Mechanical Engineering, 2009. 71 p.
7. Öman M., Nilsson L. Structural optimization of product families subjected to multiple crash load cases. Structural and Multidisciplinary Optimization. 2010. Vol. 41, no. 5. P. 797–81. DOI: 10.1007/s00158-009-0471-4
Публикации с ключевыми словами: стойки, изгиб, ударные нагрузки, МКЭ, пластические деформации, LS-DYNA, пассивная безопасность, бампер, кабина, кузов
Публикации со словами: стойки, изгиб, ударные нагрузки, МКЭ, пластические деформации, LS-DYNA, пассивная безопасность, бампер, кабина, кузов
Смотри также:
- Особенности построения конечно-элементных моделей кабин для исследования пассивной безопасности при ударе в соответствии с правилами ЕЭК ООН №29
- Разработка конечно-элементных моделей автомобильных кресел с пассивными подголовниками, отвечающих требованиям пассивной безопасности
- Решение проблемы создания конечно-элементных моделей для проектирования автомобильных кресел с активными подголовниками, отвечающими требованиям пассивной безопасности
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



