научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2012
DOI: 10.7463/1212.0482683
УДК 551.501
Россия, МГТУ им. Н.Э. Баумана
Введение.
В настоящее время одним из наиболее перспективных методов мониторинга состояния земной поверхности является авиационное зондирование. В оптическом диапазоне в большинстве случаев применяются локационные системы с пространственным сканированием и моноимпульсные системы без сканирования с импульсным излучением различной длительности (см., например, [1-6]).
В сканирующих лидарных системах продольная (вдоль направления полета) развертка обеспечивается за счет движения носителя, а поперечная - за счет углового сканирования лазерного луча. Для сокращения времени обзора (и упрощения аппаратурной реализации, особенно при большой скорости носителя) предпочтительно использовать моноимпульсные системы, основанные на излучении оптическим локатором импульса и приеме сигнала отраженного от зондируемой земной поверхности (в пределах сектора обзора приемной системы).
В работе [7] исследовались возможности моноимпульсного локационного лазерного метода обнаружения аномалий коэффициента отражения на земной поверхности. Показано, что использование метода регуляризации позволяет уверенно обнаруживать аномалии на фоне однородного (постоянного или слабо меняющегося) пространственного распределения коэффициента отражения в большом секторе обзора лазерного локатора даже в случае, когда пространственная протяженность импульса лазера в десятки раз превышает размер аномалии.
Не менее важной задачей является зондирование коэффициента отражения природных образований, которое позволяет проводить мониторинг состояния земной поверхности для различных прикладных задач (например, задач, связанных с контролем сезонных или климатических изменений).
Цель работы - исследование возможности использования моноимпульсного оптического локационного метода для измерения коэффициента отражения природных образований.
Постановка задачи.
Схема моноимпульсного зондирования показана на рисунке 1 (в плоскости XOZ, перпендикулярной направлению полета носителя).
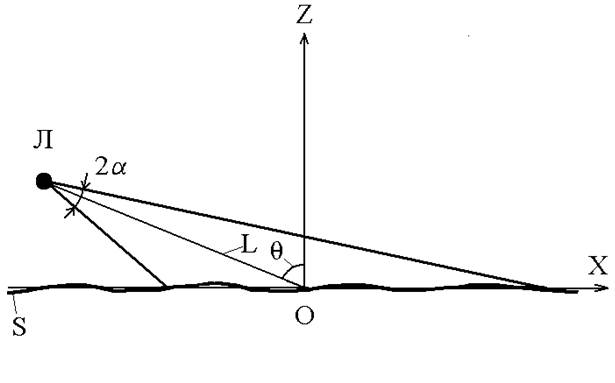
Рис. 1. Схема зондирования
На рисунке Л – локатор, расположенный на авиационном носителе; S – участок зондируемой земной поверхности (считаем его в среднем плоским); ![]() - наклонное расстояние от локатора до центра сектора обзора на поверхности;
- наклонное расстояние от локатора до центра сектора обзора на поверхности; ![]() - полный угол расходимости оптического пучка;
- полный угол расходимости оптического пучка; ![]() - угол между нормалью к плоскости z=0 и оптической осью локатора.
- угол между нормалью к плоскости z=0 и оптической осью локатора.
Здесь продольная развертка обеспечивается за счет движения авиационного носителя, а поперечная – за счет регистрации оптического импульса, отраженного от протяженного участка на земной поверхности (сектора обзора, ориентированного перпендикулярно направлению полета носителя).
При проведении энергетических расчетов для задач оптической локации в качестве модели земной поверхности в большинстве случаев (см., например, [5]) используется модель либо плоской ламбертовской поверхности, либо трехмерной случайно неровной локально-ламбертовской поверхности (с ламбертовской индикатрисой локальных участков). В [5] приведены интегральные выражения для принимаемой мощности оптического эхо-сигнала в общей схеме бистатической локации для модели земной поверхности в виде неровной локально-ламбертовской поверхности.
Будем считать поверхность слабо неровной, т.е. полагать, что ![]() ,
, ![]() , где
, где ![]() - высоты поверхности,
- высоты поверхности, ![]() - вектор наклонов поверхности. Тогда интегральное выражение для принимаемой мощности оптического эхо-сигнала
- вектор наклонов поверхности. Тогда интегральное выражение для принимаемой мощности оптического эхо-сигнала ![]() в случае коаксиальной моностатической наклонной локации (источник, приемник и их оптические оси совмещены и лежат в одной плоскости XOZ, перпендикулярной направлению полета носителя) имеет вид [5, 6]
в случае коаксиальной моностатической наклонной локации (источник, приемник и их оптические оси совмещены и лежат в одной плоскости XOZ, перпендикулярной направлению полета носителя) имеет вид [5, 6]
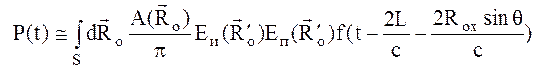 , (1)
, (1)
где
![]() - вектор в плоскости z=0;
- вектор в плоскости z=0; ![]() ;
;
![]() - пространственное распределение коэффициента отражения (альбедо) зондируемой поверхности;
- пространственное распределение коэффициента отражения (альбедо) зондируемой поверхности;
![]() ,
, ![]() - освещенности локального участка поверхности, создаваемые излучением, падающим от действительного и фиктивного (с параметрами приемника) источников [3];
- освещенности локального участка поверхности, создаваемые излучением, падающим от действительного и фиктивного (с параметрами приемника) источников [3];
![]() - форма импульса источника излучения.
- форма импульса источника излучения.
Аргумент функции 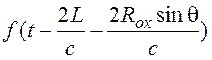 описывает задержку принимаемого оптического импульса на трассе «локатор - текущая точка на зондируемой поверхности - локатор».
описывает задержку принимаемого оптического импульса на трассе «локатор - текущая точка на зондируемой поверхности - локатор».
При зондировании земной поверхности моноимпульсным методом приемник регистрирует «протяженный» отраженный сигнал, представляющий собой последовательность элементарных сигналов, каждый из которых соответствует определенному участку местности. Анализ временной реализации ![]() отраженного сигнала потенциально позволяет определить пространственное распределение коэффициента отражения
отраженного сигнала потенциально позволяет определить пространственное распределение коэффициента отражения ![]() на земной поверхности.
на земной поверхности.
Моноимпульсный локационный метод зондирования природных образований.
Положим для простоты, что оптический пучок и поле зрения приемника имеют вид одинаковых конусов: ![]() в пределах освещенного пятна на поверхности S,
в пределах освещенного пятна на поверхности S, ![]() вне освещенного пятна;
вне освещенного пятна; ![]() в пределах поля зрения приемника на поверхности S,
в пределах поля зрения приемника на поверхности S, ![]() вне поля зрения приемника. Здесь
вне поля зрения приемника. Здесь ![]() и
и ![]() - освещенности от действительного и фиктивного (с параметрами приемника) источников и в плоскости перпендикулярной оптической оси локатора. Тогда формула (1) примет более простой вид
- освещенности от действительного и фиктивного (с параметрами приемника) источников и в плоскости перпендикулярной оптической оси локатора. Тогда формула (1) примет более простой вид
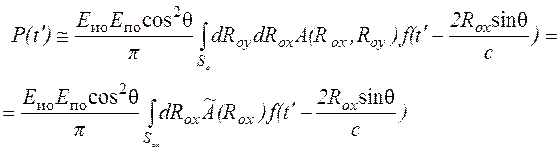 , (2)
, (2)
где  ;
;
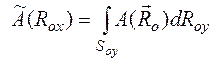 ;
;
![]() - часть поверхности S, освещенной источником.
- часть поверхности S, освещенной источником.
Если размер ![]() пятна подсвета вдоль оси OY небольшой (такой, что
пятна подсвета вдоль оси OY небольшой (такой, что ![]() практически не меняется в пределах
практически не меняется в пределах ![]() ), то выражение для
), то выражение для ![]() упрощается:
упрощается:![]() и после ряда преобразований из (2) получим:
и после ряда преобразований из (2) получим:
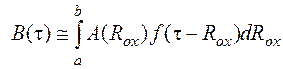 , (3)
, (3)
где
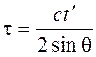 ;
;
![]() - приведенный измеренный сигнал;
- приведенный измеренный сигнал;
 ;
;
![]() - область интегрирования по
- область интегрирования по ![]() , соответствующая поверхности, освещенной источником;
, соответствующая поверхности, освещенной источником;
![]() - пространственное распределение коэффициента отражения (альбедо) зондируемой поверхности вдоль оси OX.
- пространственное распределение коэффициента отражения (альбедо) зондируемой поверхности вдоль оси OX.
Выражение (3) представляет собой интегральное уравнение первого рода типа свертки.
Для его решения может быть использован подход, основанный на переходе к дискретному аналогу интегрального уравнения первого рода [8]. Одним из вариантов такого перехода является замена интеграла на интегральную сумму по некоторой квадратурной формуле. В результате получается система линейных алгебраических уравнений
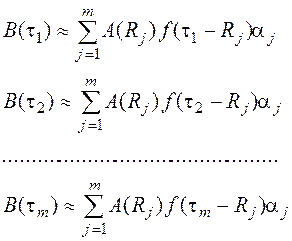 , (4)
, (4)
где
![]() - значение приведенного измеренного сигнала при
- значение приведенного измеренного сигнала при ![]() .
.
Значения коэффициентов ![]() зависят от используемой квадратурной формулы.
зависят от используемой квадратурной формулы.
В матричной форме система (4) имеет вид:
![]() , (5)
, (5)
где
![]() - искомый m-мерный вектор коэффициентов отражения с координатами
- искомый m-мерный вектор коэффициентов отражения с координатами ![]() ,
, ![]() ,
, ![]() ;
;
![]() - известный m-мерный вектор результатов измерений с координатами
- известный m-мерный вектор результатов измерений с координатами ![]() ,
, ![]()
![]() ;
;
![]() - квадратная матрица, содержащая m строк и m столбцов, с элементами
- квадратная матрица, содержащая m строк и m столбцов, с элементами ![]() :
:
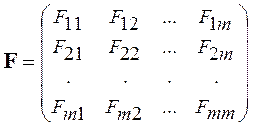 .
.
Решение уравнения (5) (если определитель матрицы ![]() отличен от нуля
отличен от нуля ![]() ) в матричной форме имеет вид
) в матричной форме имеет вид
![]() , (6)
, (6)
где
![]() - матрица обратная
- матрица обратная ![]() .
.
Математическое моделирование.
Для исследования возможностей моноимпульсного оптического локационного метода зондирования природных образований на земной поверхности проводилось математическое моделирование.
Для приближенного вычисления интеграла (3) в работе была взята формула Симпсона [9]
 , (7)
, (7)
где
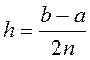 ;
; ![]() ;
; ![]() .
.
Рассматривался случай плавно меняющегося по ![]() коэффициента отражения и пространственное распределение
коэффициента отражения и пространственное распределение ![]() представлялось в виде полинома первой степени
представлялось в виде полинома первой степени
![]() .
.
Тогда, ограничиваясь в (4) и (7) всего пятью уравнениями и пятью членами квадратурной формулы, имеем
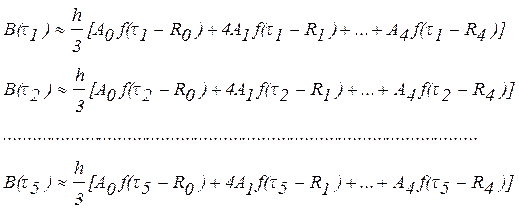 , (8)
, (8)
где  ;
; ![]() .
.
Система пяти уравнений (8) содержит пять неизвестных величин ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() и разрешима.
и разрешима.
На рисунке 2 представлены результаты восстановления величин ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() по формуле (6) без шумов и при наличии незначительного шума измерения.
по формуле (6) без шумов и при наличии незначительного шума измерения.
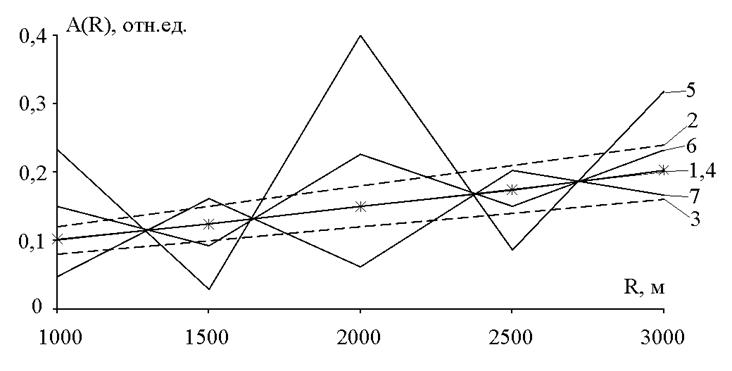
Рис. 2. Результат восстановления функции ![]() в отсутствии шумов измерения и для шумов измерения с
в отсутствии шумов измерения и для шумов измерения с ![]() =0,025 %
=0,025 %
Моделирование проводилось для пространственного распределения ![]() в виде полинома первой степени
в виде полинома первой степени ![]() +
+![]() (
(![]() =0,05 ,
=0,05 , ![]() =0,00005 м
=0,00005 м![]() ). Освещенный участок на поверхности (вдоль
). Освещенный участок на поверхности (вдоль ![]() ) задавался в пределах (1000 м, 3000 м) .
) задавался в пределах (1000 м, 3000 м) .
Форма импульса источника полагалась гауссовской
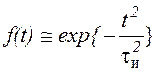 ,
,
где: ![]() - длительность импульса локатора. Тогда для функции
- длительность импульса локатора. Тогда для функции ![]() имеем
имеем
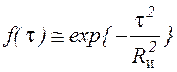 ,
,
где: ![]() - пространственная протяженность импульса локатора на зондируемой поверхности;
- пространственная протяженность импульса локатора на зондируемой поверхности; 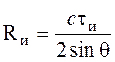 . При расчетах пространственная протяженность импульса
. При расчетах пространственная протяженность импульса ![]() полагалась равной
полагалась равной ![]() =1500 м.
=1500 м.
На рисунке 2 использованы следующие обозначения: 1 (сплошная линия) - заданное пространственное распределение коэффициента отражения ![]() ; 2, 3 (пунктирные линии) – 20 % отличие от заданного распределения; 4 (сплошная линия с маркером в виде звездочки) - восстановленное пространственные распределения в отсутствии шумов измерения; 5-7 (сплошные линии) – разные реализации восстановленных профилей пространственные распределения при относительном среднеквадратическом значении шума измерения
; 2, 3 (пунктирные линии) – 20 % отличие от заданного распределения; 4 (сплошная линия с маркером в виде звездочки) - восстановленное пространственные распределения в отсутствии шумов измерения; 5-7 (сплошные линии) – разные реализации восстановленных профилей пространственные распределения при относительном среднеквадратическом значении шума измерения ![]() = 0,025 %.
= 0,025 %.
Результаты моделирования, приведенные на рисунке 2, показывают, что в отсутствие шума измерения восстановленное пространственное распределение совпадает с заданным. Однако, даже в случае очень малых шумов измерения реализации восстановленных профилей пространственного распределения коэффициента отражения очень сильно отличаются от заданного и ведут себя как случайная функция координат.
Причиной искажения восстановленных профилей пространственного распределения коэффициента отражения является то, что компоненты вектора результатов измерений ![]() и элементы матрицы
и элементы матрицы ![]() известны только приближенно (из-за шумов измерения и ошибок процедуры дискретного интегрирования). Это приводит к неустойчивости полученного решения – малые вариации данных измерений в условиях существования ошибок (даже малых) процедуры дискретного интегрирования приводят к большим вариациям искомых коэффициентов отражения (которые могут существенно искажать действительное пространственное распределение коэффициента отражения).
известны только приближенно (из-за шумов измерения и ошибок процедуры дискретного интегрирования). Это приводит к неустойчивости полученного решения – малые вариации данных измерений в условиях существования ошибок (даже малых) процедуры дискретного интегрирования приводят к большим вариациям искомых коэффициентов отражения (которые могут существенно искажать действительное пространственное распределение коэффициента отражения).
Таким образом, задача определения пространственного распределения коэффициентов отражения ![]() природных образований по результатам измерения реализации
природных образований по результатам измерения реализации ![]() отраженного сигнала в общем случае является некорректной математической задачей и требует использования методов регуляризации [8].
отраженного сигнала в общем случае является некорректной математической задачей и требует использования методов регуляризации [8].
В работе вместо матричного уравнения (5) (эквивалентного системе уравнений (8)) было использовано близкое к нему уравнение (идея такой замены принадлежит М.М. Лаврентьеву [10])
![]() . (9)
. (9)
Соответственно, вместо уравнения (6) для нахождения неизвестных величин ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() использовалось регуляризированное решение
использовалось регуляризированное решение
![]() , (10)
, (10)
где
![]() - параметр регуляризации;
- параметр регуляризации; ![]() - единичная матрица.
- единичная матрица.
На рисунках 3 и 4 представлены результаты восстановления величин ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() по формуле (10).
по формуле (10).

Рис. 3. Результат восстановления функции ![]() с использованием метода регуляризации для пространственного распределения вида
с использованием метода регуляризации для пространственного распределения вида ![]() +
+ ![]()

Рис.4. Результат восстановления функции ![]() с использованием метода регуляризации для пространственного распределения вида
с использованием метода регуляризации для пространственного распределения вида ![]() -
- ![]()
Для рисунка 3 расчеты проводились для того же пространственного распределения и тех же параметров, что и на рисунке 2. Для рисунка 4 - для пространственного распределения ![]() в виде другого полинома первой степени
в виде другого полинома первой степени ![]() -
-![]() (
(![]() =0,25 ,
=0,25 , ![]() =0,00005 м
=0,00005 м![]() ). Параметр регуляризации находился методом невязки с учетом шума измерения и погрешности (из-за ошибок процедуры дискретного интегрирования) определения матрицы F[8].
). Параметр регуляризации находился методом невязки с учетом шума измерения и погрешности (из-за ошибок процедуры дискретного интегрирования) определения матрицы F[8].
На рисунках 3, 4 использованы следующие обозначения: 1 (сплошная тонкая линия) - заданное пространственное распределение коэффициента отражения ![]() ; 2, 3 (пунктирные линии) – 20 % отличие от заданного распределения; 4-6 (сплошные линии) – разные реализации восстановленных профилей пространственные распределения при относительном среднеквадратическом значении шума измерения
; 2, 3 (пунктирные линии) – 20 % отличие от заданного распределения; 4-6 (сплошные линии) – разные реализации восстановленных профилей пространственные распределения при относительном среднеквадратическом значении шума измерения ![]() =0,5 %.
=0,5 %.
Результаты расчетов, приведенные на рисунках 3, 4 показывают, что при наличии шума измерения восстановленное пространственное распределение удовлетворительно согласуется с заданным. Таким образом, метод регуляризации позволяет по временной реализации отраженного лазерного сигнала восстанавливать пространственное распределение коэффициента отражения для плавно меняющегося пространственного распределение коэффициента отражения. Восстановление моноимпульсным оптическим локационным методом пространственного распределения коэффициента отражения возможно в большом секторе обзора оптического локатора (размер сектора обзора при моделировании – 2 км).
В таблице 1 приведены статистические характеристики ошибок восстановления пространственного распределения коэффициента отражения - относительные (в процентах) средние по модулю (для 10![]() шумовых реализаций) погрешности определения значений
шумовых реализаций) погрешности определения значений ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() коэффициента отражения.
коэффициента отражения.
Таблица 1
Погрешности определения значений коэффициента отражения
Координата | Погрешности (в %) определения коэффициента отражения | ||
1 | 2 | 3 | |
R | 1,447 10 | 22.401 | 17.619 |
R | 872,834 | 10.231 | 5.11 |
R | 1,985 10 | 16.64 | 10.993 |
R | 623,060 | 9.543 | 6.217 |
R | 723,236 | 24.129 | 15.379 |
Здесь столбец 1 – результаты восстановления по формуле (6) для относительного среднеквадратического значения шума измерения ![]() =0,025 %; столбцы 2,3 - результаты восстановления по формуле (10) при среднеквадратическом значении шума измерения
=0,025 %; столбцы 2,3 - результаты восстановления по формуле (10) при среднеквадратическом значении шума измерения ![]() =0,5 % для параметров моделирования соответствующих рисунку 3 (столбец 2) и рисунку 4 (столбец 3).
=0,5 % для параметров моделирования соответствующих рисунку 3 (столбец 2) и рисунку 4 (столбец 3).
Результаты, приведенные на рисунках 3,4 и в таблице 1 показывают что, моноимпульсный оптический локационный метод зондирования природных образований позволяет удовлетворительно восстанавливать пространственное распределение коэффициента отражения в реальных условиях шумов измерения.
Заключение.
Таким образом, в статье предложен новый моноимпульсный оптический локационный метод зондирования природных образований. Показано, что моноимпульсный оптический локационный метод позволяет для плавно меняющегося коэффициента отражения восстанавливать его пространственное распределение в условиях шумов измерения в большом секторе обзора оптического локатора при использовании для обработки данных измерений квадратурных формул и метода регуляризации.
Список литературы
1. Сазонникова Н.А. Повышение эффективности обнаружения при лазерном зондировании поверхности // Вестник Самарского государственного аэрокосмического университета. 2009. N3 (19). С. 219-226.
2. Медведев Е.М., Данилин И.М., Мельников С.Р. Лазерная локация Земли и леса. Красноярск: Институт леса им. В.Н. Сукачева СО РАН, 2005. 182 с.
3. Матвеев И.Н., Протопопов В.В., Троицкий Н.Д., Устинов Н.Д. Лазерная локация. М.: Машиностроение, 1984. 271 c.
4. Козинцев В.И., Орлов В.М., Белов М.Л., Городничев В.А., Стрелков Б.В. Оптико-электронные системы экологического мониторинга природной среды. М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. 528 c.
5. Козинцев В.И., Белов М.Л., Орлов В.М., Городничев В.А., Стрелков Б.В. Основы импульсной лазерной локации. М.: Из-во МГТУ им. Н.Э. Баумана, 2006. 511 c.
6. . Козинцев В.И., Белов М.Л., Орлов В.М., Городничев В.А., Стрелков Б.В. Основы импульсной лазерной локации. 2-е изд., перераб. и доп. М.: Из-во МГТУ им. Н.Э. Баумана, 2010. 573 c.
7. Белов М.Л., Белов А.М., Козинцев В.И., Стрелков Б.В. Моноимпульсный локационный лазерный метод обнаружения аномалий на земной поверхности // Вестник МГТУ им. Н.Э. Баумана. Сер. Приборостроение. 2011. № 4. С. 17-24.
8. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979. 288 с.
9. Крылов В.И. Приближенное вычисление интегралов. М.: Наука, 1967. 500 с.
10. Лаврентьев М.М. О некоторых некорректных задачах математической физики. Новосибирск: Изд-воСОАНСССР, 1962. 92 с.
Публикации с ключевыми словами: оптическая локация, природные образования, коэффициент отражения, зондирование
Публикации со словами: оптическая локация, природные образования, коэффициент отражения, зондирование
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



