научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2012
DOI: 10.7463/1012.0479554
УДК 004.085; 004.33; 535.015; 535.512; 535.568; 681.7.06
Россия, г. Новосибирск, Институт автоматики и электрометрии СО РАН
Россия, МГТУ им. Н.Э. Баумана
1. Введение
Концепция микроголографической памяти, предложенная в работах [1, 2], получила значительное развитие в последние несколько лет [3-5]. Разработка многослойной оптической памяти является логическим развитием идей, заложенных в существующих дисковых системах. Такая система способна преодолеть фундаментальный предел плотности записи систем типа DVD и BlueRay, обусловленный поверхностным характером записи, обеспечив высокую плотность и емкость систем хранения данных. При таком подходе данные хранятся в виде микроголограмм, зарегистрированных в «виртуальных» слоях однородной объемной регистрирующей среды, а для записи и считывания используются сильно сфокусированные лазерные пучки. Следует отметить, что поскольку в этом случае весь объем материала является светочувствительным, то требование записи микроголограммы в произвольной точке объемной среды приводит к необходимости использования сред с нелинейным механизмом регистрации. Применение сред на основе линейного поглощения хотя и возможно, но динамический диапазон среды в этом случае расходуется неэффективно, поскольку наряду с экспонированием выбранного слоя, все остальные слои получают примерно ту же самую экспозицию. В результате полезный динамический диапазон среды составляет ~ 1/N от максимально возможного (N число слоев записи), а дифракционная эффективность микроголограмм падает в ~ N2 раз. Кроме того наличие линейного поглощения приводит к экспоненциальному затуханию интенсивности излучения, то есть запись происходит неоднородно по глубине. Поскольку фотоиндуцированное изменение свойств среды связано с поглощением света, то среди множества нелинейно-оптических эффектов можно выделить явление многофотонного поглощения. Двухфотонное поглощение наиболее сильный многофотонный процесс, но и его заметный вклад начинается при интенсивности света превышающей величину ~ 100 МВт/см2. Однако, учитывая квадратичную зависимость вероятности двухфотонного поглощения от интенсивности, и используя сильно сфокусированные световые пучки можно проводить запись локально – только в области близкой к фокусу. Следует отметить, что предельно малый размер формируемой микроголограммы (~ 2 мкм2) позволяет применять компактные импульсные лазеры с невысокой средней мощностью. Так, для получения в области записи интенсивности 1 ГВт/см2 требуется импульс излучения мощностью 20 Вт.
В этой статье мы описываем метод многослойной записи микроголограмм в фоторефрактивном кристалле нелегированного танталата лития (ТЛ) с использованием механизма двухфотонного поглощения. Метод основывается на использовании двух сфокусированных пучков света, которые пересекаются в адресуемом слое объемной среды, где и записывается микроголограмма. Компьютерно-управляемый пьезопозиционер используется для сканирования материала и записи микроголограмм в других слоях. Приводятся данные по записи матрицы микроголограмм в 20 слоях и распределению ошибок считывания по глубине.
2. Метод записи/считывания
Принцип метода многослойной записи микроголограмм представлен на рисунке 1. Для записи микроголограмм используются два когерентных сфокусированных пучка света: опорный 1 и гетеродинный 2 [6]. Эти пучки пространственно совмещаются в произвольном слое объемной регистрирующей среды 3, и в области их пересечения записывается голограмма 4. Голограммы в других слоях записываются путем перемещения зоны пересечения пучков по глубине объемной среды 3. В случае использования излучения с длиной волны λ = 0,53 мкм, фокусирующего объектива с числовой апертурой NA = 0,6 и среды с показателем преломления n = 2,18 (танталат лития) размеры голограммы по уровню ½ максимальной интенсивности составляют по осям X, Y и Z соответственно 1,4×1,4×12 мкм3. Голограмма имеет пространственную частоту ~ 1000 л/мм и содержит всего 2-3 штриха. Голограмму такого предельно малого размера будем далее называть микроголограммой.
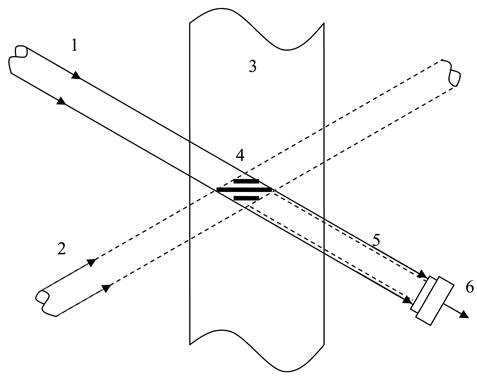
Рис. 1. Схема, иллюстрирующая метод многослойной оптической записи и коллинеарного гетеродинного считывания двоичной информации
Для селекции зоны считывания в объеме регистрирующего материала 3 используется метод коллинеарного гетеродинирования [7]. В этом случае частота света гетеродинного пучка 2 сдвигается на ωг = 2π×fг (fг = 88 МГц) относительно частоты опорного пучка 1 и бегущая интерференционная решетка, образовавшаяся в зоне пересечения пучков 1 и 2, совмещается с микроголограммой 4, записанной в адресуемом слое. Световой пучок 5 образующийся в результате дифракции пучка 2 на микроголограмме 4 вследствие точного совпадения пространственных частот бегущей и записанной интерференционных решеток будет распространяться по одному пути (коллинеарно) с пучком 1. В результате взаимодействия двух коллинеарных пучков с различными частотами света на выходе фотоприемника 6 появляется фототок с разностной частотой ωг, несущий информацию о микроголограмме и ее характеристиках. Важно отметить, что гетеродинное считывание происходит только в зоне пересечения опорного и гетеродинного пучков света. Вследствие этого метод обладает высокой помехозащищенность по отношению к шумам рассеяния оптических элементов, материала диска и всех неадресуемых информационных слоев.
Метод гетеродинного считывания обладает уникальной возможностью восстанавливать не только амплитуду, но и, что важно для информационных технологий, фазу микроголограммы. Это позволяет применять фазовый способ кодирования информации [8, 9]. Последний, как известно [10], обеспечивает более высокую помехозащищенность, чем амплитудное кодирование с пассивным нулем, когда логической единице соответствует наличие света, а логическому нулю – его отсутствие.
Информационным параметром в предлагаемом методе кодирования является разность фаз пространственных решеток двух следующих друг за другом микроголограмм. В процессе считывания определяется разность фаз ∆φ и по кодовой таблице находится соответствующее значение двоичного разряда. Применение четырехуровневого относительного фазового кодирования приводит к удвоению плотности и скорости записи. Принцип простейшего двухуровневого (противофазного) относительного фазового кодирования иллюстрируется рисунком 2. Здесь схематически показаны положения максимумов интенсивности в последовательности из трех микроголограмм. Фаза решетки каждой следующей микроголограммы изменяется на π радиан.
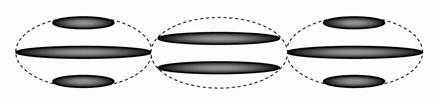
Рис. 2. Последовательность из трех микроголограмм, у которых фазы соседних решеток сдвинуты на π рад
Исследование процессов двухфотонной записи объемных микроголограмм и их последующего коллинеарного гетеродинного считывания проводилось на экспериментальной установке, оптическая схема которой приведена на рис. 3.
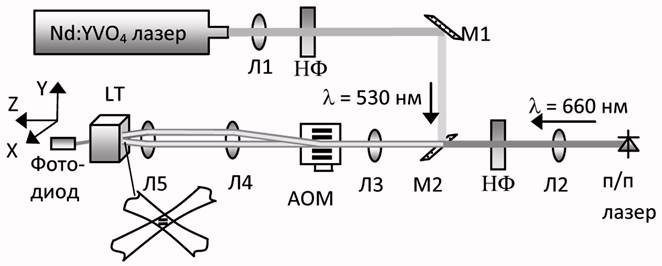
Рис. 3. Оптическая схема установки для многослойной двухфотонной записи и гетеродинного считывания микроголограмм
Для записи микроголограмм используется излучение второй гармоники твердотельного лазера на основе Nd:YVO4 с внутрирезонаторным электрооптическим модулятором (λ = 0,53 мкм, длительность импульса τp = 1,7 нс). Максимальная частота повторения импульсов – 10 кГц. Излучение коллимируется линзой Л1, а с помощью линзы Л3 формируется перетяжка в акустооптическом модуляторе (АОМ). Пучок, полученный в результате дифракции, и нулевой пучок с помощью телескопической системы (Л4, Л5) переносятся в заданный по глубине слой кристалла ТЛ. В этом слое в результате интерференции формируется микрорешетка. Ее поперечный размер составляет X × Y = 1,4 × 1,4 мкм2, а пространственная частота – 1090 л/мм. Максимальная интенсивность излучения в плоскости регистрации составляет I = 8 ГВт/см2. Для гетеродинного считывания микроголограмм использован полупроводниковый лазер с мощностью 8 мВт и длиной волны λ = 0,66 мкм. Излучение лазера коллимируется линзой Л2, затем проходит через ту же оптическую систему, что и записывающие пучки и формирует микрорешетку в том же самом месте и с той же пространственной частотой.
Дифракционная эффективность микроголограмм при коллинеарном гетеродинном считывании определяется следующим образом. Как уже упоминалось выше, на фотодиод попадает два коллинеарных световых пучка. Один из них – гетеродинный, продифрагировавший предварительно на АОМ (имеет сдвиг частоты) и далее на микроголограмме, второй пучок – опорный, прошедший АОМ без дифракции. Фотодиод производит гетеродинирование и на его выходе возникает переменный ток, частота которого равна сдвигу частоты света, а выражение для амплитуды iр может быть записано в следующем виде
iр = 2(iгiоп)1/2, (1)
где iг и iоп – фототоки полученные раздельно из гетеродинного и опорного пучков. Если дифракционная эффективность АОМ равна 50 %, и обозначая величину фототока при выключенном модуляторе i0 получим iг =ηi0/2, iоп = i0/2. Подставляя выражения для iг и iоп в (1) можно найти η = (iр/i0)2. Амплитуда изменения показателя преломления Δn может быть вычислена из формулы Когельника [11] для фазовых пропускающих голограмм. Для определения амплитуды изменения показателя преломления нужно также знать размер микроголограммы по глубине (вдоль оси Z). Этот размер был определен путем сканирования микроголограммы по оси Z. При записи в кристалле ТЛ он оказался равным Δz = 12 мкм. Этот размер очень важен, поскольку он определяет разрешение по глубине и, следовательно, предельное число слоев записи.
Для записи использовался конгруэнтный кристалл ТЛ. Концентрация железа в кристалле не превосходит величины 3×1017 см-3, поэтому его можно считать условно чистым. Ось C кристалла размером 12×8×2 мм располагалась параллельно как поверхности образца, так и плоскости падения интерферирующих пучков. Записывающие и считывающие пучки на длинах волн 0,53 мкм и 0,66 мкм соответственно имели необыкновенную поляризацию.
3. Экспериментальное исследование параметров многослойной записи
Исследование двухфотонной записи проводилось следующим образом: два остросфокусированных пучка с длиной волны 0,53 мкм пересекаются в заданном по глубине (в диапазоне 10 – 400 мкм) слое ТЛ. Несмотря на то, что ТЛ прозрачен для излучения на этой длине волны, одновременное поглощение двух фотонов приводит к фотоиндуцированному изменению его свойств и формированию объемной микроголограммы.
В работе [3] показано, что зависимость амплитуды модуляции показателя преломления от интенсивности записывающих пучков имеет квадратичный характер, что подтверждает двухфотонный характер записи. Насыщенное значение амплитуды модуляции показателя преломление для этого кристалла ТЛ составляет ∆ns = 10,8×10-4 и достигнуто при интенсивности излучения I = 4,1 ГВт/см2, при этом характерное время записи составляет величину τ = 32 нс. Для сравнения отметим, что в работе [12], при экспонировании легированного железом конгруэнтного ТЛ непрерывным лазером получены значения τ ~ 2 сек, а ∆ns = 1×10-5. В свою очередь в работе [13] при двухступенчатом возбуждении мощными импульсами лазера получены значения τ = 500 нс и ∆ns = 1,6×10-4.
Отсюда следует, что двухфотонное межзонное фотовозбуждение электрона приводит к значительно более быстрому отклику по сравнению с традиционным случаем, когда возбуждение происходит с примесного уровня.
Процесс записи микроголограмм проводится в старт-стопном режиме, в то время как процесс считывания – в режиме непрерывного сканирования. На рис. 4 приведен пример считывания последовательности из 4-х микроголограмм, расположенных вдоль оси Х на глубине 100 мкм. Расстояние между соседними микроголограммами составляет 2 мкм. Все голограммы записаны с одной и той же фазой. Запись проводилась последовательностью из 10 импульсов, а суммарная интенсивность записывающих пучков 7 ГВт/см2. На рис. 4а показано распределение амплитуд сигнала считывания, полученных на выходе фотодиода (рис. 3). Измерения размеров отклика на уровне ½ максимального значения амплитуды показали, что они равны 1,65 – 1,75 мкм. Учитывая, что результат считывания является сверткой записанной и считывающей микрорешеток, а размер считывающей микрорешетки составляет 0,8 мкм, получим, что размер микроголограммы по оси Х находится в области 1,45 – 1,5 мкм. Характер изменения фазы сигнала приведен на рис. 4б. В области вне зоны записи, где наблюдается лишь шумовой сигнал, фаза распределена случайным образом в диапазоне от -π до π. В тоже время в области, где записаны микроголограммы, фаза постоянна, что соответствует условию эксперимента.
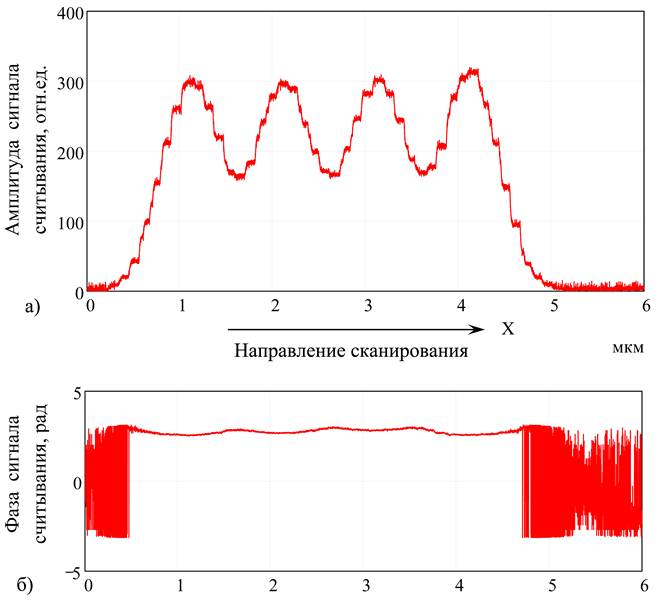
Рис. 4. Результаты считывания строки из четырех микроголограмм, зарегистрированных в нелегированном ТЛ: а) амплитуда сигнала считывания; б) фаза сигнала считывания
Характер изменения размера отклика по глубине среды представлен на рис. 5. На глубине среды от 50 мкм до 400 мкм была проведена запись последовательности из 10 микроголограмм, расстояние между которыми было равно 35 мкм. Ширина отклика по уровню ½ максимального значения амплитуды составляет 11,8 мкм в первом слое и плавно возрастает до 16,8 мкм по мере увеличения глубины до 385 мкм. Таким образом, в этом диапазоне глубин расстояние между слоями нельзя сделать меньше 17 мкм. Следует отметить, что при проведении записи/считывания не применялась коррекция сферической аберрации фокусирующего микрообъектива (Л5), связанная с изменением глубины слоя, в котором происходит запись микроголограмм.
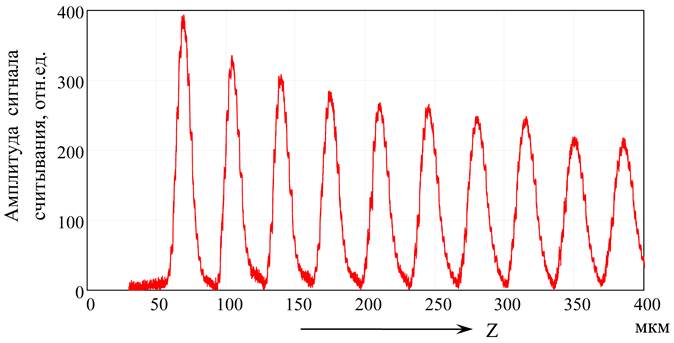
Рис. 5. Сигнал считывания при сканировании по глубине кристалла ТЛ, в котором
10 микроголограмм были зарегистрированы на различной глубине
4. Анализ аддитивных шумов
Все аддитивные шумы, действующие в системе записи/считывания, можно условно разделить на две большие группы: к первой относятся те шумы, отдельные реализации которых представляют функции времени; другие шумы обусловлены структурой голограммы и описываются функциями пространственных координат.
Первая группа включает тепловые и дробовые шумы электронных устройств, а также избыточный шум излучения полупроводникового лазера. Для уменьшения таких шумов необходимо сужать полосу пропускания устройства считывания, что, в конечном итоге, приводит к уменьшению скорости чтения информации.
Из второй группы наиболее существенными являются шумы рассеяния оптических элементов и регистрирующего материала. Уровень этих шумов зависит от полосы пространственных частот пропускания оптической схемы, сужение которой с целью снижения пространственных шумов приводит к уменьшение плотности записи – важнейшего параметра оптического ЗУ.
Найдем зависимость основных источников шумовот параметров элементов устройства записи/считывания, дадим оценку минимального их значения с целью сравнения с результатами экспериментального исследования.
Основными источниками шумов, распределенных во времени, являются:
дробовой шум iдр фототока Iф
iдр=(2eIф∆f )1/2= (2eγP∆f )1/2, (2)
где e – заряд электрона, P – постоянная составляющая мощности света на входе фотоприемника, γ= Iф /P – чувствительность фотодиода, ∆f – полоса частот;
шум интенсивности излучения полупроводникового лазера (избыточный шум)
iшл=Iф(𝛽∆f )1/2, (3)
где β имеет смысл спектральной плотности относительных флюктуаций интенсивности излучения лазера. Величина β зависит от спектрального состава продольных мод излучения, уровня обратного рассеяния, попадающего в резонатор лазера и др.
Нами проведено экспериментальное сравнение уровня шумов на выходе фотоприемника при освещении его когерентным светом лазерного диода DL – 6147 – 040 (λ = 0,658 мкм) с дробовым шумом фототока при некогерентном освещении. Из сравнения выражений (2) и (3) видно, что уровень iшл относительно iдр возрастает с увеличением Iф, поэтому измерения выполнялись при относительно больших значениях фототока Iф = 0,5 мА. Мощность излучения на выходе лазера составляла 20 мВт, в качестве коллиматора использовался микрообъектив ОМ – 27. Результаты серии измерений показали, что избыточные шумы излучения полупроводникового лазера на частоте 80 МГц превышают уровень дробового шума максимум на 5 %, что находится в пределах ошибки эксперимента. Таким образом, в системе считывания информации можно не учитывать избыточные шумы современных одночастотных полупроводниковых лазеров.
Шумовой ток фотоприемника iш,ф зависит от трех источников: генератора напряжения теплового шума фотодиода и приведенных ко входу усилителя генераторов шумового тока и напряжения. Обозначим Sш,ф интегральную спектральную плотность шумов фотоприемника на базе p-i-n фотодиода. Тогда значение шумового тока, приведенного ко входу усилителя фотоприемника, составит
iш,ф=( Sш,ф∙∆f )1/2. (4)
Исходя из условия максимального контраста бегущей считывающей интерференционной решетки, принимаем мощности опорного Pоп и гетеродинного Pг одинаковыми. Тогда переменная (сигнальная) составляющая фототока при коллинеарном гетеродинном детектировании определяется выражением
iс= 2 γ(PсPг )1/2=2 γ Pг [η (1–η)]1/2≈2Iф η1/2, (5)
где Pс=η Pоп= η Pг – мощность дифрагированного (сигнального) пучка, η << 1 – дифракционная эффективность микрорешетки.
Принимаем допустимую вероятность ошибки равной 10-5 (уровень вполне достаточный для эффективной работы системы помехоустойчивого кодирования). Дальнейшее уменьшение вероятности ошибки нецелесообразно, поскольку преобладающими становятся ошибки, обусловленные межсимвольной интерференцией. При восьмиуровневой относительной фазовой модуляции и допустимой вероятности ошибок 10-5 отношение сигнал/шум (С/Ш) при когерентном приеме должно быть не менее 7,72 [14].
Учитывая перечисленные выше составляющие шумового тока (2), (4), найдем значение минимальной дифракционной эффективности микрорешетки, при которой обеспечивается допустимая вероятность ошибки
ηmin>(С/Ш)2[(e/2Iф)+( Sш,ф /4Iф2)]∙∆f, (6)
Найдем ηmin для гетеродинной системы считывания с параметрами:
максимальная скорость считывания Vсч=100 Мбит/с;
мощность излучения лазера Pл=20 мВт;
к.п.д. оптической системы от выхода лазера до входа фотоприемника ρ = 0,2, т.е. Pоп+ Pг= ρ Pл=4 мВт;
чувствительность фотодиода γ = 0,4 А/Вт, поэтому Iф= γ Pоп= 0,8 мА;
порог чувствительности фотоприемника на основе p-i-n фотодиода составляет ориентировочно 3∙10–11 Вт/Гц1/2, соответственно Sш,ф = 1,44∙10–22 А2/Гц.
Тогда из (5) получим ηmin > 10–7.
Таким образом, проведенный анализ свидетельствует о том, что временные шумы не являются существенной причиной, ограничивающей быстродействие гетеродинного считывания информации.
Рассмотрим влияние пространственно распределенных шумов регистрирующего материала. При гетеродинном способе чтения голограмма освещается двумя световыми пучками: нулевым – a0= a0 exp(j νt) и гетеродинным – aг = aгexp {j [(ν+ωг)t+φг]}. Здесь a0, aг, φг – амплитуды и начальная фаза соответствующих световых волн; ν, ν+ωг – круговые частоты излучения лазера и гетеродинного пучка соответственно.
В плоскости фотоприемника при чтении происходит интерференция трех коллинеарных световых пучков: опорного (aоп), сигнального (aс) и шумового (aш). Поскольку
aоп >> aс >> aш, то можно записать
aоп≈ CГa0;
aс=CГaгη1/2exp(j φс)=aсexp{ j[(ν+ωг)t +φ+ φс]};
aш=CГaгηш1/2exp(j φш)=aшexp{ j[(ν+ωг)t +φ+ φш]};
Здесь CГ ≈ 1 – коэффициент пропускания света (по амплитуде) голограммы; ηш – дифракционная эффективность шумовых решеток.
Суммарная мощность света Pф и пропорциональный ей фототок определяются выражением
Pф~| aоп+ aс+ aш|2= aоп2+ aс2+ aш2+2 aсaш cos(φс – φш)+
+ 2 aопaсcos(ωгt+ φ+ φс)+ 2 aопaшcos(ωгt+ φ+ φш). (7)
Из выражения (7) следует, что только два последних слагаемых несут полную информацию об амплитуде aс и фазе φс сигнала. Этот сигнал является узкополосным процессом, поскольку ширина его спектра значительно меньше центральной частоты ωг. Такой сигнал может быть представлен суммой двух ортогональных колебаний с частотой ωг и случайными амплитудами [15]. Для выделения амплитуды и фазы этих составляющих сигнал с выхода фотоприемника подается на два синхронных детектора (балансных модулятора), где умножается на два ортогональных опорных напряжения, имеющих круговую частоту ωг. После низкочастотной фильтрации на выходах фильтров нижних частот получаем значения cos (UC) и sin (US) составляющих сигнала.
UC=2Kaоп[aш cos(φ+ φш)+ aс cos(φ+ φс)], (8)
US=–2Kaоп[aш sin(φ+ φш)+ aс sin(φ+ φс)]. (9)
Здесь K – суммарный коэффициент преобразования мощности Pф фотоприемником и балансным смесителем.
По величине ортогональных напряжений UC и US(8), (9) можно определить амплитуду a суммы полезного сигнала aс и шума aш.
U= (UC2+ US2)1/2=2Kaоп[aс2+aш2+2 aсaш.cos(φш– φс)]1/2=2Kaоп a. (10)
Значение Uш определялось экспериментально путем измерения сигнала рассеяния от движущейся среды при aс = 0. Среднеквадратичное значение напряжения шума оказалась равной 1,9 мВ. Амплитуда суммы шума Uш и сигнала Uр от записанной решетки составила U = 125 мВ. Поскольку U >> Uш , то Uр ≈ U, а отношение сигнал/шум достигает значения (С/Ш) = Uр / Uш ≈ 65,8.
Такое большое значение (С/Ш) может быть либо при очень высокой дифракционной эффективности решетки либо при крайне малом уровне шумов рассеяния света регистрирующим материалом. Величина последнего оценивается, как известно [16], дифракционной эффективностью шумовых решеток Φ в единичной полосе двумерной пространственной частоты. Например, у фотопластинок в области пространственной частоты порядка 1000 мм–1 минимальное значение Φ достигает 0,5∙10–9 мм2, у стекла – 10–10 мм2.
Однако следует заметить, что существующие методики измерения шумов рассеяния образцов материалов «на просвет» неадекватны способу послойной записи информации, так как зачастую большая доля шумов рассеяния сосредоточена в приповерхностном слое материала и обусловлена микрошероховатостями его поверхности.
Значение дифракционной эффективности шумовых решеток ηш в глубине материала, которое оценивалось по величине Uш, составило ηш = 4∙10–7.
Эффективная полоса пространственных частот считывающего гауссова эллиптического пучка, имеющего радиусы перетяжки по уровню 1/e2 максимальной интенсивности rx = 0,68 мкм и ry = 1,25 мкм, составляет B = (1/2π rx ry) = 1,9∙105 мм–2. В результате получим: Φ= ηш /B = 2,1∙10–12 мм2. Оценим также дифракционную эффективность микроголограммы: ηг= ηш (С/Ш)2= 1,7∙10–3.
Таким образом, показано, что столь большое значение (С/Ш) ≈ 65,8 достигается за счет крайне низкого уровня рассеяния света в глубине материала.
5. Экспериментальное исследование достоверности регистрации информации
Для определения влияния на достоверность регистрации нестабильности запуска твердотельного лазера, а также шумов рассеяния регистрирующего материала была проведена запись последовательности из 150 микроголограмм с одной и той же фазой. На рис. 6 приведена гистограмма разности фаз. Видно, что нет ни одного случая выброса за значение ± π/8. Таким образом, шумы рассеяния среды и джиттер лазера не препятствуют проведению записи с восемью уровнями фазы.
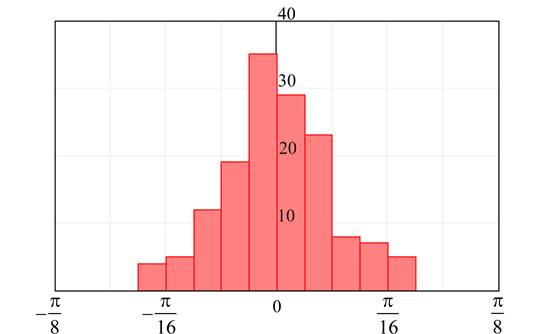
Рис. 6. Гистограмма распределения разности фаз в последовательности из 150 микроголограмм, записанных с одной и той же фазой
Для получения информации о практической плотности записи, учитывающей межсимвольную и межстрочную интерференцию, была проведена запись трехмерной матрицы 36×6×20 микроголограмм. Схема расположения микроголограмм приведена на рис. 7.
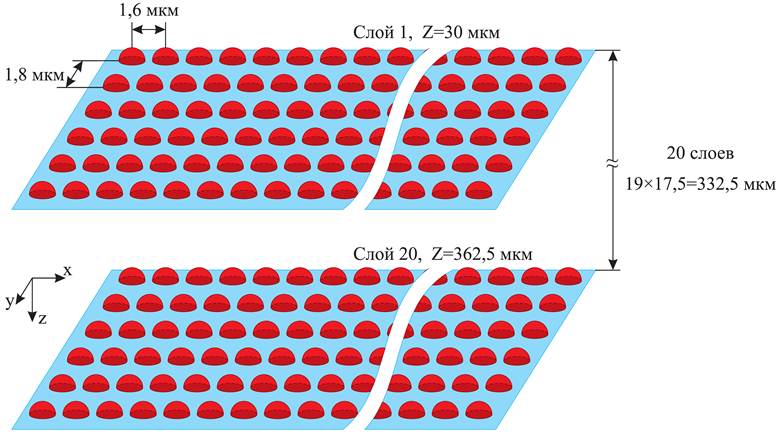
Рис. 7. Схема расположения микроголограмм в трехмерной матрице
Расстояния между голограммами 1,6 мкм, 1,8 мкм и 17,5 мкм соответственно по осям Х, Y и Z были выбраны близкими к размерам откликов (по уровню ½). При записи использовалось четырехуровневое фазовое кодирование. Величина защитного интервала в этом случае составляет ±π/4. Считывание считается достоверным, если разница между заданным значением разности фаз двух соседних микроголограмм и значением, полученным в процессе считывания, лежит внутри этого защитного интервала. Гистограмма распределения такой разницы для всего массива из 4320 микроголограмм приведена на рис. 8.
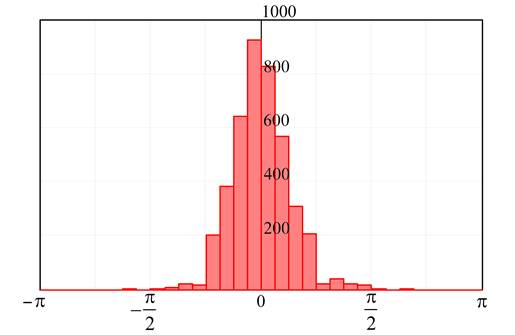
Рис. 8. Гистограмма распределения отклонения разности фаз от заданной. Массив – 4320 микроголограмм. Четырехуровневая относительная фазовая модуляция
Общее число ошибок считывания равно 152, а вероятность их появления составляет 3,5 × 10-2. Следует отметить, что ошибки распределены по глубине неоднородно, что показано на рис. 9.
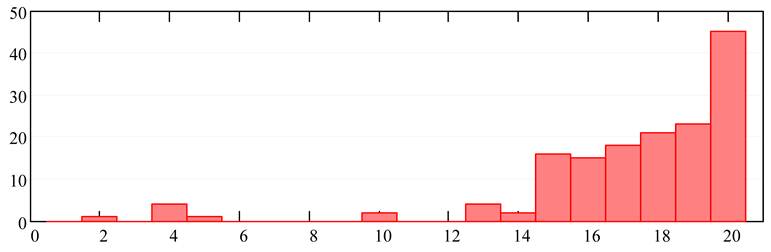
Рис. 9. Гистограмма распределения ошибок считывания по слоям
Из данных, приведенных на этом рисунке видно, что вплоть до 15 слоя количество ошибок незначительно (вероятность появления ошибки – 4,8 × 10-3), но их величина резко возрастает в последних 5 – 6 слоях (вероятность появления ошибки – 0,11). Такое увеличение количества ошибок можно связать с ростом сферической аберрации выходного микрообъектива при записи на глубинах 250 – 400 мкм. Таким образом, при указанных выше условиях записи, предложенный метод позволяет проводить запись примерно 14 слоев на глубину до 300 мкм без коррекции сферической аберрации.
Плотность записи, полученная с учетом четырехуровневого фазового кодирования, в данном эксперименте составляет величину 4 × 1010 бит/см3. Плотность записи может быть повышена при оптимизации заполнения выходного микрообъектива и соответственного уменьшения размеров микроголограммы.
6. Заключение
Оптическая нелинейная двухфотонная запись позволяет эффективно использовать динамический диапазон регистрирующего материала, а также улучшить однородность записи по глубине среды, благодаря чему удается реализовать многослойную запись даже на материалах с относительно низким изменением показателя преломления.
Разработана и экспериментально апробирована установка для многослойной оптической регистрации информации. Микроголограмма формируется путем совмещения двух сфокусированных лазерных пучков в объеме регистрирующей среды. В результате в зоне пересечения пучков образуется объемная интерференционная решетка, размер которой по уровню ½ максимальной интенсивности составляет: по глубине материала – 12 мкм, а в плоскости среды – 1,4 × 1,4 мкм2. Записанная информация представлена в виде многоуровневой относительной фазовой модуляции решеток, что позволяет увеличить плотность и скорость записи. Метод коллинеарного гетеродинного считывания информации позволяет восстановить амплитуду и фазу микроголограммы. Высокая пространственная селективность при записи и считывании информации позволяет реализовать многослойную оптическую память с использованием толстых регистрирующих материалов.
Проведена запись массива микроголограмм в 20-и слоях на глубине от 30 мкм до 362 мкм. Получены данные об ошибках считывания и распределении их в зависимости от глубины записи слоя. В этом эксперименте реализована плотность записи 4 × 1010 бит/см3.
Показано, что можно пренебречь влиянием аддитивных шумов на скорость чтения и плотность записи информации на движущийся носитель из-за практически полного отсутствия избыточных шумов излучения у современных одночастотных полупроводниковых лазеров, устранения при нелинейной двухфотонной записи негативного влияния эффекта наложения голограмм и, наконец, крайне низкого уровня рассеяния света в глубине регистрирующего материала.
Эксперименты по записи и считыванию информации в 20-и слоях показали, что доминирующим источником ошибок является межсимвольная интерференция, влияние которой резко возрастает на глубине 15-го слоя.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации, в рамках государственного контракта от 28.04.2011 № 16.513.12.3006 по ФЦП "Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы".
Списоклитературы
1. Rudakov I.B., Steinberg I.Sh., Shepetkin Ju.A. Multilayer optical information recording // Optoelectronics, Instrumentation, and Data Processing. 1991. No. 3. P. 83–86.
2. Eichler H.J., Kuemmel P., Orlic S., Wappelt A. High density disk storage by multiplexed microholograms // IEEE Journal of Selected Topics in Quantum Electronics. 1998. Vol. 4, no. 5. P. 840–848. DOI: http://dx.doi.org/10.1109/2944.735770
3. Steinberg I.Sh., Shepetkin Y.A. Two–photon recording of microholograms in undoped lithium tantalate // Applied Optics. 2008. Vol. 47, no. 1. P. 9–14. DOI: http://dx.doi.org/10.1364/AO.47.000009
4. McLeod R., Daiber A., McDonald M., Robertson T., Slagle T., Sochava S., Hesselink L. Microholographic multilayer optical disk data storage // Applied Optics. 2005, Vol. 44, no. 16. P. 3197–3207. DOI: http://dx.doi.org/10.1364/AO.44.003197
5. Saito K., Horigome T., Miyamoto H., Yamatsu H., Tanabe N., Hayashi K., Fujita G., Kobayashi S., Kudo T., Uchiyama H. Drive system and readout characteristic of Micro-Reflector optical disc // Optical Data Storage, OSA Technical Digest Series (CD). Optical Society of America, 2007. Paper MB1. Available at: http://www.opticsinfobase.org/abstract.cfm?URI=ODS-2007-MB1 , accessed 03.11. 2012.
6. Штейнберг И.Ш., Щепеткин Ю.А. Способ многослойной оптической записи и воспроизведения двоичной информации: а. с. 1769233 СССР. 1989.
7. Карлтон Х., Мэлони В., Мелц Г. Коллинеарное гетеродинирование в оптических процессорах // ТИИЭР, 1969, Т. 57, № 5, С. 32–40. [Carleton H.R., Maloney W.T., Meltz G. Collinear Heterodyning and Optical Processors // Proceedings of the IEEE. May 1969. Vol. 57, no. 5. P. 769-775. DOI: 10.1109/PROC.1969.7071 ].
8. Вовк Ю.В., Щепеткин Ю.А. Способ записи голограмм: а. с. 1457663 СССР. 1983.
9. Вовк Ю.В., Щепеткин Ю.А. Способ голографической регистрации двоичной информации: а. с. 1349547 СССР. 1986.
10. Помехоустойчивость и эффективность систем передачи информации / Под ред. А.Г.Зюко. М.: Радио и связь, 1985. 271 c.
11. Kogelnik H. Coupled wave theory for thick hologram gratings. Bell Syst. Tech. Journal.
November 1969. Vol. 48, no. 9. P. 2909–2947. Available at: http://www.alcatel-lucent.com/bstj/vol48-1969/articles/bstj48-9-2909.pdf , accessed 03.11. 2012.
12. Imbrock J., Kip D., Krätzig E. Nonvolatile holographic storage in iron–doped lithium tantalate with continuous–wave laser light // Optic Letters. 1999. Vol. 24, no. 18. P. 1302–1304. DOI: http://dx.doi.org/10.1364/OL.24.001302
13. Imbrock J., Wevering S., Buse K., Krätzig E. Nonvolatile holographic storage in photorefractive lithium tantalate crystals with laser pulses // J. Opt. Soc. Am. B. 1999. Vol. 16, no. 9. P. 1392–1397. DOI: http://dx.doi.org/10.1364/JOSAB.16.001392
14. Заездный А.М., Окунев Ю.Б., Рахович Л.М. Фазоразностная модуляция и ее применение для передачи дискретной информации. М.: Связь, 1967. 304 c.
15. Зиновьев А.Л., Филиппов Л.И. Введение в теорию сигналов и цепей. М.: Высшая школа, 1968. 264 c.
16. Кольер Р., Беркхарт К., Лин Л. Оптическая голография. М.: Мир, 1973. 686 c. [Collier R.J., Burckhardt K.B., Lin L.H. Optical Holography. Academic Press, New York, 1971.].
Публикации с ключевыми словами: многослойная память, двухфотонное поглощение, гетеродинирование, фазовое кодирование
Публикации со словами: многослойная память, двухфотонное поглощение, гетеродинирование, фазовое кодирование
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



