научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2012
DOI: 10.7463/1012.0479419
УДК 621.83.05
Россия, КФ МГТУ им. Н.Э. Баумана
nasonovda@yandex.ru
Работоспособность, прочность и виброактивность зубчатых редукторов, выполненных по планетарной схеме, в значительной степени зависит от равномерности распределения нагрузки по параллельным потокам передаваемой мощности (между сателлитами) [1, 2]. В свою очередь, соблюдение названного условия во многом определяется погрешностями изготовления и сборки сателлитных узлов [3].
В работе [1] предложено в процессе сборки редуктора минимизировать указанные погрешности посредством регулировки межцентровых расстояний сателлитов с помощью эксцентриковых втулок, устанавливаемых в расточки водила под опорные шейки их осей. Однако для реализации данного предложения необходимо максимально точное определение фактических значений погрешностей сателлитных узлов, что, как показывает опыт одного из ведущих отечественных производителей планетарных редукторов большой мощности [3], является весьма нетривиальной задачей.
Рассматриваемые погрешности рассчитываются по данным технологических карт контроля точности, заполняемых специалистами ОТК завода-изготовителя на основе результатов прямых и косвенных измерений первичных ошибок изготовления элементов планетарной ступени в рамках «комплексного точностного параметра» (далее «КТП») планетарного механизма.
Изначально «КТП» был разработан для планетарных редукторов с прямозубыми цилиндрическими зубчатыми колесами [1]. Впоследствии он был распространен на шевронное зацепление и неоднократно уточнялся [4] Последняя уточненная версия «КТП» была приведена в работе [5], где на основе экспериментальных данных была выявлена корреляция указанного параметра с зубцовой вибрацией планетарного редуктора.
Согласно [5], комплексные погрешности изготовления и сборки сателлитных узлов шевронного планетарного редуктора могут быть определены, как
 . (1)
. (1)
Здесь ![]() - погрешности суммарных зазоров в зацеплениях полушевронов сателлитов с центральными колесами для случая, когда нумерация сателлитов от i до zc совпадает с направлением окружных сил на их осях (с направлением крутящего момента на солнечной шестерне), причем погрешности вычисляются отдельно для каждого полушеврона;
- погрешности суммарных зазоров в зацеплениях полушевронов сателлитов с центральными колесами для случая, когда нумерация сателлитов от i до zc совпадает с направлением окружных сил на их осях (с направлением крутящего момента на солнечной шестерне), причем погрешности вычисляются отдельно для каждого полушеврона;
![]() - угол зацепления в торцовом сечении (делительный угол профиля в торцовом сечении), определяемый из соотношения
- угол зацепления в торцовом сечении (делительный угол профиля в торцовом сечении), определяемый из соотношения
 ,
,
где ![]() - угол профиля исходного контура рейки в нормальном сечении,
- угол профиля исходного контура рейки в нормальном сечении,
![]() - угол наклона зуба на делительном цилиндре;
- угол наклона зуба на делительном цилиндре;
 - накопленные ошибки хордальных расстояний между первой и i-й осями расточек в щеках водила;
- накопленные ошибки хордальных расстояний между первой и i-й осями расточек в щеках водила;
![]() ,
, ![]() - погрешности диаметральных зазоров в соединениях осей с сателлитами и водилом, отнесенные к полушевронам сателлитов:
- погрешности диаметральных зазоров в соединениях осей с сателлитами и водилом, отнесенные к полушевронам сателлитов:
![]() ;
; ![]() ,
,
где ![]() - погрешности диаметров расточек под оси в щеках водила,
- погрешности диаметров расточек под оси в щеках водила,
![]() - погрешности средних по длине полушевронов диаметров расточек в сателлитах под оси,
- погрешности средних по длине полушевронов диаметров расточек в сателлитах под оси,
![]() - погрешности диаметров посадочных шеек осей под установку в щеки водила,
- погрешности диаметров посадочных шеек осей под установку в щеки водила,
![]() - погрешности средних по длине полушевронов диаметров посадочных поверхностей осей под сателлиты;
- погрешности средних по длине полушевронов диаметров посадочных поверхностей осей под сателлиты;
![]() - погрешности отнесенных к полушевронам тангенциальных составляющих эксцентриситетов посадочной поверхности i-й оси под сателлит относительно ее посадочных поверхностей под установку в водило;
- погрешности отнесенных к полушевронам тангенциальных составляющих эксцентриситетов посадочной поверхности i-й оси под сателлит относительно ее посадочных поверхностей под установку в водило;
![]() - постоянные составляющие погрешности толщины зубьев i-го сателлита по полушевронам.
- постоянные составляющие погрешности толщины зубьев i-го сателлита по полушевронам.
При использовании выражения (1) для расчета «КТП» наибольшие трудности возникают с определением хордальных расстояний между расточками под сателлиты в водиле (![]() ), что связано с отсутствием у большинства отечественных производителей редукторов большой мощности современного высокоточного оборудования, позволяющего получать координаты расточек столь крупногабаритных и имеющих сложную геометрию узлов, как водило (рис. 1), путем прямых измерений.
), что связано с отсутствием у большинства отечественных производителей редукторов большой мощности современного высокоточного оборудования, позволяющего получать координаты расточек столь крупногабаритных и имеющих сложную геометрию узлов, как водило (рис. 1), путем прямых измерений.
На практике ошибки взаимного расположения расточек в водиле определяются по результатам измерения межцентровых расстояний и скрещивания, специальных контрольных валов, устанавливаемых с заданной точностью в указанные расточки. В общем случае измерениям на каждой из щек водила подлежат расстояния между осями расточек под сателлиты и центральной осью водила (далее - радиальные межцентровые расстояния) и между осями соседних расточек под сателлиты (далее - хордальные межцентровые расстояния). Скрещивания осей определяются для расточек водила под сателлиты относительно центральной оси и между осями соседних расточек под сателлиты.

Рис. 1 Модель водила планетарного редуктора с пятью сателлитами
В работе [1] из всех названных параметров для определения искомых погрешностей изготовления водила рекомендуется использовать только хордальные межцентровые расстояния, пренебрегая всеми остальными измерениями. Представляется, что такое искусственное сужение используемых в расчетах исходных данных едва ли оправдано, поскольку может давать значительное отклонение получаемых результатов от фактических значений искомых ошибок.
Для повышения точности их определения в работе [6] были предложены математическая модель и алгоритм численного решения, позволившие получать искомые координаты расточек под сателлиты в водиле с учетом всех контролируемых параметров. При этом были преодолены вычислительные трудности, связанные с необходимостью решения переопределенной (из-за значительно возросшего числа исходных данных) и несовместной (из-за неизбежных погрешностей измерения) системы уравнений.
Рассмотрим указанную модель и соответствующий ей алгоритм численного решения на примере определения координат расточек под оси для водила планетарной ступени с пятью сателлитами (рис. 1).
Для составления модели введем декартову систему координат с центром в плоскости носовой щеки водила таким образом, чтобы центральные расточки водила определяли координатную ось Х, а центр расточки под ось первого сателлита определял направление координатной оси Y (рис. 1). Обозначения остальных параметров иллюстрируют рис. 2-4.
На рис. 2 точками P0 и P′0 обозначены центры левой и правой расточек водила под опорные шейки, точками P1 и P′1 – центры расточек под ось первого сателлита. Из-за погрешностей изготовления точка P′1 может отклоняться от плоскости, определяемой точками P1, P0 и P′0, а величина этого отклонения S1 характеризует скрещивание оси первого сателлита относительно центральной оси водила, принимаемой за базу (ось Х, рис. 1).
В результате измерений радиальных межцентровых расстояний водила определяются величины R1÷R5, R′1÷R′5, S1÷S5 (рис 3). За положительное значение Si на рис.3 принято смещение точки P′i относительно Piвокруг оси X (ось P0-P′0) против часовой стрелки, если смотреть с конца оси X, штрихами обозначены центры расточек на правой щеке, без штрихов – на левой.

Рис. 2. Схема измерения взаимного расположения расточек под ось первого сателлита
относительно центральной оси водила

Рис 3. Вид на центры расточек (Pi, P′i ) водила с конца оси Х
Измерением хордальных межцентровых расстояний водила и скрещивания осей соседних расточек под сателлиты определяются величины hi=|PiPi-1| (рис. 4), h′i=|P′iP′i-1| и di(геометрическая интерпретация параметра δi (рис. 5) рассмотрена ниже), где i=1÷5. При этом, в силу цикличности индексации, имеем h1=|P1P5|,h′1=|P′1P′5|. Нумерация центров расточек Pi осуществляется против часовой стрелки, если смотреть с конца оси Х.
Если в качестве допущения считать, что обе щеки водила параллельны, т.е. центры всех расточек лежат либо в плоскости YZ (левая щека), либо в плоскости, параллельной YZ (правая щека), то можно не сводя задачу к двухмерной, исключить из расчетов координату X.
Учитывая, что точки P0, P′0 приняты за базовые, а направление оси Y определяется центром первой расточки (координата z точки P1 равна нулю), в качестве неизвестных имеем y-z координаты центров расточек под оси сателлитов на левой и правой щеках, т.е. 19 величин.
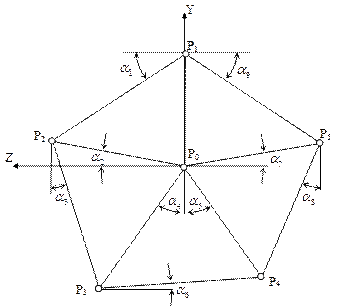
Рис. 4. Схема расположения центров расточек в плоскости щеки водила YZ (P)
и угловых величин для тригонометрических соотношений (α)
Обозначив угловые величины в соответствии с рис. 4, можно записать группу из 19 тригонометрических соотношений связывающих результаты измерений и координаты центров расточек на левой щеке водила (9 неизвестных):
 (2)
(2)
Аналогичные 20 уравнений, которые можно записать относительно y-zкоординат центров расточек на правой щеке (10 неизвестных), дополняют систему (2). Угловые величины в системе (2) взяты в предположении, что точки P1 – P5 (рис. 4) и P′1 – P′5 образуют правильные пятиугольники. На самом же деле, при наличии погрешностей изготовления водила, правильность этих пятиугольников нарушается. Следовательно, зависимость расчетных координат от измеряемых параметров носит нелинейный характер, а система (2) представляет собой линеаризованную математическую модель, позволяющую, как показано ниже, получать приемлемые для практического использования приближенные решения.
Для учета всех имеющихся результатов измерений, запишем еще две группы уравнений. Первую группу получим из рассмотрения скрещивания осей расточек под сателлиты относительно центральной оси водила. Так, например, для расточки под ось сателлита №2 (i=2), параметр s2 (рис. 3) будет связывать координаты только центров расточек P2 и P′2, поскольку центральная ось является базой:
 (3)
(3)
С учетом параметров скрещивания s1 – s5 система (3) содержит 9 уравнений относительно все тех же 19 неизвестных, названных выше.
Вторая группа уравнений получается при анализе скрещивания δ осей расточек под соседние сателлиты. В этом случае, в отличие от предыдущего, ни одна из осей не является базовой, и параметр δ связывает не две, а четыре точки. На рис. 5, поясняющем геометрический смысл параметра δi, показан вид на i-ю и (i-1)-ю расточки со стороны конца оси Х.
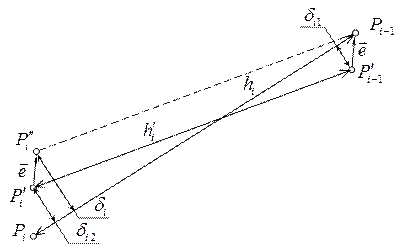
Рис 5. Вид на центры расточек под оси соседних сателлитов со стороны конца оси Х (рис. соответствует i = 2)
Величина δi характеризует скрещивание i-й и (i-1)-й осей расточек и состоит из двух компонент: δi=δi2-δi1, где δi1 и δi2 – расстояния от точек P′i-1 и P′i до линии Pi-1-Pi, в проекции на плоскость YZ. Причем за положительное значение принимается величина δ, если P′i (P′i-1) и P′0 (центр водила) располагаются по разные стороны от линии Pi-1-Pi. Ту же величину имеем при измерении расстояния от точки P″i до линии Pi-1-Pi (точка P″i получается путем параллельного переноса P′i на вектор e, совмещающий точки P′i-1 и Pi-1). Именно эта величина и подлежит непосредственному контролю в процессе измерений, когда, согласно принятой технологии измерений, за базу принимается (i-1)-я ось.
Параметр δ2, например, позволяет записать следующие, входящие в систему четыре, уравнения:
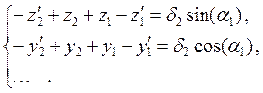 (4)
(4)
Система (4), учитывающая параметры δi÷δ5, содержит десять уравнений.
После объединения систем (2), (3) и (4), получается система из пятидесяти восьми уравнений относительно девятнадцати неизвестных, представляющая собой математическую модель, пригодную для вычисления погрешностей изготовления водила по результатам их косвенных измерений, и учитывающую, в соответствии с поставленной задачей, все имеющиеся результаты.
Как уже отмечалось, данная система является не только переопределенной и несовместной (из-за погрешностей измерений), но и преднамеренно линеаризованной с целью максимального упрощения. Для ее решения был разработан итерационный алгоритм [6], позволяющий преодолеть последствия использованных упрощений.
Согласно данному алгоритму первое приближенное решение полученной системы уравнений ищется с использованием геометрических параметров αi(рис. 4), определяемых в предположении, что искомые координаты расточек водила под сателлиты образуют правильные пятиугольники. Далее угловые величины αi уточняются с использованием результатов первой итерации, и расчет повторяется. Последующие приближения рассчитываются аналогичным образом до достижения требуемой точности.
Критерием точности получаемых результатов на каждой итерации служит сумма квадратов невязок (разностей между левыми и правыми частями уравнений уточненной обобщенной системы, при подстановке в неё вычисленных на последней итерации неизвестных), свидетельствующая о степени отклонения расчетных величин от измеряемых. Стабильное уменьшение этой величины, отмеченное при решении тестовых примеров, свидетельствует о хорошей сходимости итерационного процесса [6].
В связи с повышенными требованиями к точности расчетов описанный алгоритм реализован в пакете символьных вычислений Стивена Вольфрама «Mathematica», позволяющем производить расчеты с любой наперед заданной точностью, независимо от разрядности используемой машины [7].
Анализ результатов выполненных тестовых расчетов показал, что одной из особенностей описанной математической модели является то, что при равноценности всех используемых в качестве исходных данных результатов измерений, их влияние на искомые координаты расточек под сателлиты в водиле существенно различается. Это происходит из-за того, что тригонометрические функции, находящиеся в правой части уравнений (2)-(4), играют роль весовых коэффициентов, и получаемое решение неизбежно «смещается» в сторону тех параметров, при которых стоят большие весовые коэффициенты.
При попытке перенести эти коэффициенты в левую часть, обусловленность системы, к решению которой приводит метод наименьших квадратов, резко ухудшается и сходимость решения недопустимо падает. Дело в том, что синусы некоторых углов в окрестностях решения столь малы, что перенос их в левую часть подобен делению на ноль. С другой стороны, вклад исходных данных (результатов измерений), при которых стоят близкие к нулю коэффициенты, в конечный результат вычислений столь ничтожен, что эти уравнения можно исключить из системы практически без потери точности.
На основании изложенного разработанная ранее модель была упрощена путем исключения из нее четырех уравнений, содержащих множитель sin(α6), и переноса тригонометрических функций в левую часть, что исправляет допущенную ранее некорректность. Далее по тексту в ссылках на используемую математическую модель будет иметься в виду исправленная система уравнений.
Дальнейший анализ модели выявил еще одно важное свойство, благодаря которому можно существенно повысить достоверность расчетов. Оказалось, что в силу переопределенности системы и характера взаимосвязи результатов косвенных измерений, из нее можно исключить все уравнения, связанные с любым (но одним) из результатов измерений. При этом ранг матрицы коэффициентов системы не становится меньше числа неизвестных, что дает возможность ее приближенного решения.
Подставляя полученное решение «усеченной» таким образом системы уравнений в исключенные из нее уравнения, и решая их относительно исключенного параметра, можно получить его ожидаемое значение. Степень отклонения ожидаемого значения от измеренного, вполне может играть роль критерия достоверности данного параметра.
Если принять допущение, что в исходных данных (а это 30 результатов измерений) присутствует не более одной грубой ошибки, то процесс диагностирования и исключения такой ошибки легко автоматизируется и решается без человеческого участия.
Задача сводится к поочередному исключению из исходных данных каждого из результатов измерений и вычисления его ожидаемого значения. Если величина отклонения, какого-либо из результатов измерений от его ожидаемого значения больше некоторой заданной величины, то такой замер считается ошибочным, а в качестве наилучшего приближенного решения выбирается решение, полученное без учета этого результата измерения. Если величина максимального отклонения по всем измерениям не превышает заданной величины, то наилучшим считается решение, полученное с помощью полной системы (без исключения уравнений).
На рис.6 показаны среднеквадратичные отклонения исключаемых результатов измерений от их ожидаемых значений, вычисляемые по формуле
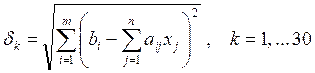 ,
,
где k – номер исключаемого измерения;
a, b, x – коэффициенты системы [A]{X}={B}, составленной из уравнений, исключенных из модели;
m, n – размерность матрицы [A]. Правые части этих уравнений содержат значение исключенного измерения, а вектор {X} – решение «усеченной» системы уравнений, т.е. вычисленные координаты центров расточек.
Из рис. 6 видно, что δ1 – отклонение первого параметра от ожидаемого значения, вычисленного по приведенной выше методике, максимально, что вполне соответствует тестовому набору исходных данных, где все замеры, кроме первого, соответствуют идеально изготовленной конструкции, а параметр № 1 (это результат измерения R1 согласно рис. 3) отклоняется на 0,1 мм от номинального размера (600 мм). Наличие незначительных отклонений остальных параметров объясняются влиянием первого параметра, присутствующего в уравнениях при определении этих отклонений.

Рис. 6. Среднеквадратичные отклонения результатов измерений от их ожидаемых значений: ось абсцисс – порядковый номер исключаемого измерения, ось ординат – величина отклонения (мм)
При наличии более одной грубой ошибки в исходных данных, их диагностирование не так очевидно, особенно если величина ошибок одного порядка. Тем не менее, это возможно, но не в автоматизированном, а в ручном режиме путем анализа визуализированных результатов расчетов.
На рис. 7 приведен пример визуализации результатов тестовых расчетов с ошибочным результатом измерения R1, причем на рис.7а отображены результаты решения при исключении из модели измерения R1, а на рис.7б – без исключения R1. Доверительные интервалы и отклонения центров расточек отображаются с соответствующим масштабным коэффициентом. Область 1 – доверительные интервалы положения центров расточек осей сателлитов (определяются расчетной точностью измерений). Центры областей 2 и 3 указывают положения центров расточек под оси сателлитов в правой и левой щеках водила.
а)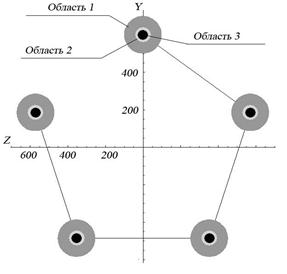 б)
б)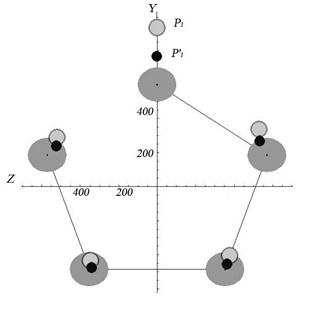
Рис. 7. Визуализация результатов тестовых расчетов с ошибочным измерением R1.
Использование найденных описанным выше способом (с учетом всех контролируемых заводом-изготовителем точностных характеристик водила) координат расточек под оси сателлитов в водиле для расчета параметров ![]() позволяет повысить достоверность определения искомых комплексных погрешностей изготовления и сборки сателлитных узлов в соответствии с (1), что имеет важное практическое значение.
позволяет повысить достоверность определения искомых комплексных погрешностей изготовления и сборки сателлитных узлов в соответствии с (1), что имеет важное практическое значение.
Вместе с тем, имеющиеся экспериментальные и расчетные данные [5, 8-10] показывают, что для дальнейшего повышения корректности определения результативной точности зубчатых зацеплений и ее влияния на нагруженность и виброактивность планетарного редуктора необходимо учитывать не только входящие в (1) первичные погрешности изготовления его деталей и узлов, но и нагрузочно-скоростные характеристики конкретных режимов эксплуатации.
Последние влияют на фактические погрешности зубчатых зацеплений в процессе работы редуктора вследствие упругих деформаций его элементов под нагрузкой, а также смещений зубчатых колес в пределах зазоров и на жесткостях опор под действием усилий в зацеплениях, весовых нагрузок и центробежных сил.
Работы в указанном направлении ведутся.
Список литературы
1. Айрапетов Э.Л., Генкин М.Д. Статика планетарных механизмов. М.: Наука, 1976. 264 с.
2. Айрапетов Э.Л., Генкин М.Д. Динамика планетарных механизмов. М.: Наука, 1980. 256 с.
3. Леонтьев Ю.А., Ямпольский И.Д., Хомяков В.П., Леонтьев М.Ю. Опыт создания на ОАО «КТЗ» судовых редукторов большой мощности // Юбилейный сборник трудов Научно-исследовательского Центра ОАО «Калужский Турбинный Завод». Калуга: Манускрипт, 2002. С.134-144.
4. Леонтьев М.Ю. Исследование статической нагруженности мощных судовых планетарных редукторов: дисс. …канд. техн. наук. М.: ИМАШ РАН, 2001. 229 с.
5. Леонтьев М.Ю., Полунин И.В., Лысенков В.С. Анализ влияния точности изготовления редукторов ГТЗА на виброактивность // Материалы V научно-технической конференции «Взгляд в будущее». СПб.: ФГУП «ЦКБ МТ «Рубин», 2007. С. 319-328.
6. Леонтьев М.Ю., Насонов Д.А. Об алгоритме численного решения одной из некорректно заданных задач, представляющей практический интерес // Материалы V Общероссийской научно-практической конференции с международным участием «Актуальные вопросы современной науки и образования». Вып. 2. Красноярск: Научно-инновационный центр, 2010. С. 280-287.
7. Дьяконов В.П. Mathematica 4 с пакетами расширений. М.: «Нолидж», 2000. 608 с.
8. Айрапетов Э.Л., Апархов В.И., Бедный И.А., Леонтьев М.Ю. Расчетные исследования малонагруженных планетарных передач // Теория и практика зубчатых передач: труды международной конференции. Ижевск: Изд-во ИжГТУ, 1996. С. 141-146.
9. Айрапетов Э.Л., Апархов В.И., Бедный И.А., Леонтьев М.Ю. Влияние весовой нагрузки зацеплений на динамику крупногабаритных планетарных передач // Procееdingsofthe5-thInternationalConference «Dynamicsofmachineaggregates».Gabcikovo, Slovak Republic, 2000.
10. Леонтьев М.Ю., Насонов Д.А. К вопросу о влиянии погрешностей изготовления и деформаций сателлитного узла на динамику планетарного редуктора // Материалы всероссийской научно-технической конференции «Наукоемкие технологии в приборо- и машиностроении и развитие инновационной деятельности в ВУЗе». Т. 1. М.: Изд. МГТУ им. Н.Э. Баумана, 2008. С. 76-81.
Публикации с ключевыми словами: математическое моделирование, планетарный редуктор, некорректно заданные задачи
Публикации со словами: математическое моделирование, планетарный редуктор, некорректно заданные задачи
Смотри также:
- Математическая модель перспективного испытательно-измерительного тренажерного стенда для освоения и оценки работоспособности специального оборудования быстроходных машин
- 77-48211/638257 О преподавании учебной дисциплины “Математическое моделирование”
- 77-30569/242041 Синтез концептуальной динамически параметризованной модели системы разнородных комплексов специального вооружения
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



