научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2012
DOI: 10.7463/1112.0479190
УДК. 53.098
Россия, Волгоградский государственный университет
yakimets_volsu@mail.ru
1. Введение
Исследования, посвященные изучению взаимодействию взаимно перпендикулярных магнитных полей в нелинейных магнетиках имеют почтенный возраст [1]. Как правило, в качестве такой нелинейной среды рассматривают ферромагнитные материалы и среды [2]. Одним из практических результатов таких исследований стала разработка феррозондовых магнитометров, обладающих рекордной (для не квантовых измерителей) чувствительностью [3]. Вместе с тем, хотя современная теория ферромагнетизма не позволяет аналитически описывать гистерезис, анализ работы феррозонда [2] показывает, что гистерезисные потери являются фундаментальным ограничением порога чувствительности феррозондовых магнитометров.
Существенно повысить чувствительность, быстродействие электронной аппаратуры возможно при переходе к более низким температурам, в частности при использовании в измерительной и вычислительной технике сверхпроводящих материалов. Электродинамика сверхпроводников в диапазоне радиочастот, на котором энергия кванта существенно меньше ширины энергетической щели, с достаточной точностью описывается уравнениями Гинзбурга – Ландау [4]. Хорошо известно, что сверхпроводники так же как и ферромагнетики обладают нелинейными магнитными свойствами. Более того, вытекающая из уравнений Гинзбурга – Ландау нелокальность взаимодействия сверхпроводящего конденсата куперовских пар с магнитным полем оказывает существенное влияние на генерацию высших гармоник в радиочастотном диапазоне [5].
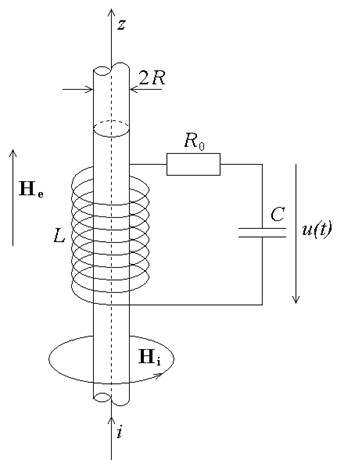
Рисунок 1. Сверхпроводящий провод во внешнем поле
Поскольку потери в сверхпроводниках в радиочастотном диапазоне пренебрежимо малы, нелинейная восприимчивость сверхпроводников второго рода с успехом используется для измерения слабых магнитных полей [6, 7]. Вместе с тем все существующие сверхпроводниковые магнитометры основаны на взаимодействии параллельных магнитных полей – измеряемого постоянного поля и радиочастотного поля накачки, то есть повторяют конструкцию классического феррозонда с продольным возбуждением. Можно ожидать, что нелинейное взаимодействие взаимно перпендикулярных магнитных полей в сверхпроводниках, рассматриваемых как нелинейный проводящий магнетик [8], позволит разработать магнитометры, не уступающие по чувствительности квантовым, например, сквидам [9, 10]. Улучшение чувствительности возможно благодаря тому, что объем, в котором происходит нелинейное взаимодействие, гораздо больше объема джозефсоновского контакта в сквиде.
Несмотря на большое количество публикаций, посвященных нелинейной электродинамике сверхпроводников второго рода, вопрос о нелинейном взаимодействии взаимно перпендикулярных магнитных полей в них до сих пор не рассматривался. Задачей работы является описание этого взаимодействия по аналогии с классической работой [1] для ферромагнетиков с помощью уравнений Гинзбурга – Ландау и аналитическое решение полученных нелинейных уравнений для предельного случая проволоки толщиной меньше лондоновской глубины проникновения методом последовательных приближений. Цель работы – оценить потенциальную чувствительность криозонда, использующего взаимодействие взаимно перпендикулярных магнитных полей в сверхпроводнике второго рода в задачах магнитометрии.
2. Постановка задачи
Пусть зондом сверхпроводникового магнитометра, который можно назвать криозондовым, является тонкая проволока из сверхпроводника второго рода диаметром ![]() , причем
, причем ![]() , где
, где ![]() – длина когерентности, а
– длина когерентности, а ![]() – глубина проникновения. Запишем для проволоки, находящейся во внешнем продольном однородном магнитном поле He, по которой течет ток
– глубина проникновения. Запишем для проволоки, находящейся во внешнем продольном однородном магнитном поле He, по которой течет ток ![]() (рис. 1), уравнения Гинзбурга-Ландау [4]:
(рис. 1), уравнения Гинзбурга-Ландау [4]:
![]() , (1)
, (1)
![]() , (2)
, (2)
![]() , (3)
, (3)
где ![]() - вектор нормали к поверхности сверхпроводника,
- вектор нормали к поверхности сверхпроводника, ![]() – нормированный параметр порядка,
– нормированный параметр порядка, ![]() – векторный потенциал магнитного поля,
– векторный потенциал магнитного поля, ![]() – квант магнитного потока.
– квант магнитного потока.
Выберем цилиндрическую систему координат так, чтобы ось z совпадала с осью проволоки. Пусть напряженность внешнего магнитного поля равна ![]() . Магнитное поле, создаваемое током, имеет вид
. Магнитное поле, создаваемое током, имеет вид ![]()
![]() . Выберем калибровку вектор потенциала
. Выберем калибровку вектор потенциала ![]()
![]() таким образом, чтобы функция
таким образом, чтобы функция ![]() была вещественной. Тогда уравнения (1) - (3) сводятся к нелинейным дифференциальным уравнениям (4) - (6) с действительными коэффициентами и граничным условиям (7) к ним:
была вещественной. Тогда уравнения (1) - (3) сводятся к нелинейным дифференциальным уравнениям (4) - (6) с действительными коэффициентами и граничным условиям (7) к ним:
 , (4)
, (4)
![]() , (5)
, (5)
![]() , (6)
, (6)
 (7)
(7)
3. Методика решения
В силу симметрии задачи можно считать, что параметр порядка Ψ и вектор потенциал ![]() зависят только от координаты
зависят только от координаты ![]() . Тогда из уравнения (6) следует
. Тогда из уравнения (6) следует ![]() , что согласуется с первым граничным условием (7) Таким образом, вектор
, что согласуется с первым граничным условием (7) Таким образом, вектор ![]() имеет только
имеет только ![]() и
и ![]() компоненты:
компоненты: ![]() . Введем безразмерную координату
. Введем безразмерную координату ![]() и безразмерные компоненты вектор-потенциала
и безразмерные компоненты вектор-потенциала ![]() ,
, ![]() где
где ![]() , и обозначим
, и обозначим ![]() ,
, ![]() – малые параметры. Тогда уравнения (4), (5) и (7) принимают вид
– малые параметры. Тогда уравнения (4), (5) и (7) принимают вид
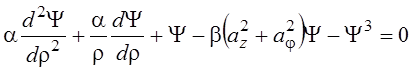 , (8)
, (8)
 , (9)
, (9)
 , (10)
, (10)
 (11)
(11)
Если потребовать дополнительно, чтобы при ![]() выполнялись условия:
выполнялись условия:
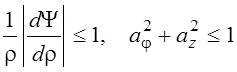 , (12)
, (12)
то уравнения (8) – (10) можно решать методом последовательных приближений, положив ![]() . Подставляя это разложение в уравнение (8) и приравнивая коэффициенты при соответствующих степенях
. Подставляя это разложение в уравнение (8) и приравнивая коэффициенты при соответствующих степенях ![]() и
и ![]() , получим
, получим ![]() ,
, ![]() ,
, ![]() . Тогда уравнения (9) – (12) принимают вид:
. Тогда уравнения (9) – (12) принимают вид:
 , (13)
, (13)
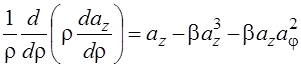 , (14)
, (14)
 , (15)
, (15)
 . (16)
. (16)
Найдем приближенное решение уравнений (13) и (14), используя метод регулярного разложения по малому параметру ![]() , в виде:
, в виде:

С учетом граничных условий (15) в нулевом приближении, приравнивая коэффициенты при соответствующих степенях, получим:
 ,
,
где ![]() и
и ![]() – модифицированные функции Бесселя первого рода нулевого и первого порядков, соответственно.
– модифицированные функции Бесселя первого рода нулевого и первого порядков, соответственно.
Используя известное фундаментальное решение уравнения [11], следующее приближение решения уравнения (13) имеет вид:
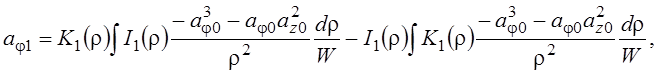
где ![]() - детерминант Вронского,
- детерминант Вронского, ![]() – модифицированная функция Бесселя второго рода первого порядка. Тогда приближенное решение второго уравнения системы (8) может быть записано следующим образом:
– модифицированная функция Бесселя второго рода первого порядка. Тогда приближенное решение второго уравнения системы (8) может быть записано следующим образом:
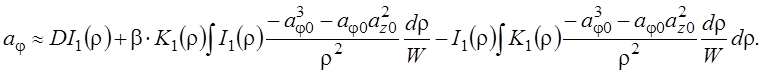
Оценим величину магнитного потока через поперечное сечение сверхпроводящей проволоки. Приближенно вычисляя интегралы, входящее в последнее выражение, раскладывая модифицированные функции Бесселя вблизи нуля (![]() ) и ограничиваясь линейными по
) и ограничиваясь линейными по ![]() слагаемыми, получим:
слагаемыми, получим:
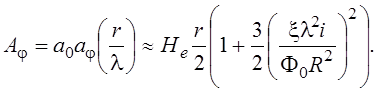
Откуда:
 (17)
(17)
где ![]() - критическая плотность тока [12],
- критическая плотность тока [12], ![]() ,
, ![]() – площадь поперечного сечения зонда.
– площадь поперечного сечения зонда.
Оценим порог чувствительности криозондового магнитометра. Пусть по зонду протекает переменный ток ![]() , создающий в нем плотность тока
, создающий в нем плотность тока ![]() , близкую к критической. Положим
, близкую к критической. Положим ![]() . Как и в феррозондовом магнитометре, сверхпроводящая проволока является сердечником LC контура с резонансной частотой близкой к
. Как и в феррозондовом магнитометре, сверхпроводящая проволока является сердечником LC контура с резонансной частотой близкой к ![]() (рис. 1). Если катушка индуктивности является длинным соленоидом, содержащим
(рис. 1). Если катушка индуктивности является длинным соленоидом, содержащим ![]() витков, то:
витков, то:
 , (18)
, (18)
где ![]() постоянное или медленно меняющееся измеряемое магнитное поле,
постоянное или медленно меняющееся измеряемое магнитное поле, ![]() – заряд на конденсаторе
– заряд на конденсаторе ![]() .
.
Колебания в резонансном контуре описываются уравнением:
 . (19)
. (19)
Подставляя в уравнение (19) выражение (17) для магнитного потока через сверхпроводящий зонд с учетом соотношения (18), получим дифференциальное уравнение второго порядка:
 , (20)
, (20)
где обозначено ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Поскольку ![]() , найдем решение уравнения (20) методом последовательных приближений в виде
, найдем решение уравнения (20) методом последовательных приближений в виде ![]() . В нулевом приближении, система описывается уравнением:
. В нулевом приближении, система описывается уравнением:
 .
.
Решение имеет вид:
 .
.
При точной настройке контура (![]() ) для выходного напряжения преобразователя получаем:
) для выходного напряжения преобразователя получаем:
 , (21)
, (21)
где ![]() – добротность контура,
– добротность контура, ![]() – поток измеряемого магнитного поля
– поток измеряемого магнитного поля ![]() через поперечное сечение сверхпроводникового зонда.
через поперечное сечение сверхпроводникового зонда.
Из формулы (21) видно, что напряжение на контуре ![]() осциллирует с частотой
осциллирует с частотой ![]() синхронно с переменным током
синхронно с переменным током ![]() , текущим по проволоке, что позволяет использовать метод синхронного детектирования. Амплитуда
, текущим по проволоке, что позволяет использовать метод синхронного детектирования. Амплитуда ![]() выходного напряжения пропорциональна измеряемому магнитному полю
выходного напряжения пропорциональна измеряемому магнитному полю ![]() , причем крутизна преобразования растет с увеличением частоты
, причем крутизна преобразования растет с увеличением частоты ![]() .
.
Известно, что глубина проникновения переменного электромагнитного поля зависит от его частоты. Критическую частоту, при которой это изменение становится существенным, можно оценить из выражения для комплексной глубины проникновения [12]:
 ,
,
где ![]() ,
, ![]() - плазменные частоты сверхпроводящих и нормальных электронов, их значения порядка 1010 … 1011 Гц,
- плазменные частоты сверхпроводящих и нормальных электронов, их значения порядка 1010 … 1011 Гц, ![]() - эффективная частота столкновений, равная 1010 Гц,
- эффективная частота столкновений, равная 1010 Гц, ![]() - частота электромагнитного поля. Таким образом, изменение глубины проникновения в
- частота электромагнитного поля. Таким образом, изменение глубины проникновения в ![]() происходит на частоте порядка
происходит на частоте порядка ![]() Гц и для рабочей частоты 30 МГц ей можно пренебречь. При низких температурах легко получить для контура, содержащего
Гц и для рабочей частоты 30 МГц ей можно пренебречь. При низких температурах легко получить для контура, содержащего ![]() витков добротность
витков добротность ![]() . Если
. Если ![]() , то коэффициент пропорциональности в формуле (21) между амплитудой выходного напряжения
, то коэффициент пропорциональности в формуле (21) между амплитудой выходного напряжения ![]() и потоком Ф измеряемого магнитного поля составит
и потоком Ф измеряемого магнитного поля составит ![]() .
.
4. Результаты и обсуждение
Собственное шумовое напряжение измерительного усилителя, приведенное к входу, имеет величину порядка 1 нВ в полосе 1 Гц, тогда порог чувствительности криозондового магнитометра по магнитному потоку 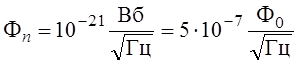 не уступает лучшим сквидам [9, 10] при том, что конструкция сверхпроводникового зонда гораздо проще и технологичнее. По сути, сверхпроводниковый зонд очень похож на криотрон [9], в котором вентиль является зондом, а управляющая катушка – резонансным контуром.
не уступает лучшим сквидам [9, 10] при том, что конструкция сверхпроводникового зонда гораздо проще и технологичнее. По сути, сверхпроводниковый зонд очень похож на криотрон [9], в котором вентиль является зондом, а управляющая катушка – резонансным контуром.
Требование ![]() фактически использовалось только для упрощения расчетов. При практических применениях достаточно выбирать
фактически использовалось только для упрощения расчетов. При практических применениях достаточно выбирать ![]() , в этом случае взаимодействие скрещенных полей будет происходить по всему объему сверхпроводника. При этом для магнитометрии нужны "плохие" сверхпроводники – с большой глубиной проникновения и малой плотностью критического тока, например ВТСП-керамика с пониженным содержанием кислорода вблизи перехода. При температуре 77 К эффективная глубина проникновения в керамическом сверхпроводнике порядка 100 мкм [13].
, в этом случае взаимодействие скрещенных полей будет происходить по всему объему сверхпроводника. При этом для магнитометрии нужны "плохие" сверхпроводники – с большой глубиной проникновения и малой плотностью критического тока, например ВТСП-керамика с пониженным содержанием кислорода вблизи перехода. При температуре 77 К эффективная глубина проникновения в керамическом сверхпроводнике порядка 100 мкм [13].
Поскольку в соответствии с формулой (17) поток переменного магнитного поля через сечение сверхпроводника не зависит от направления тока в нем, сверхпроводящую проволоку диаметром 0,1 мм можно уложить "змейкой" так, чтобы в соседних звеньях ток протекал в противоположных направлениях. Зонд магнитометра диаметром 1 мм будет состоять из 100 таких звеньев и позволит получить порог чувствительности по магнитному полю порядка  . Такая чувствительность является рекордной даже для квантовых магнитометров и позволит проводить предельные измерения в области гео- и био-магнетизма. Отметим, что в отличие от сквидов, сигнальная характеристика криозондового магнитометра не является периодической, поэтому такой магнитометр может измерять абсолютное значение магнитной индукции, а не только ее изменение.
. Такая чувствительность является рекордной даже для квантовых магнитометров и позволит проводить предельные измерения в области гео- и био-магнетизма. Отметим, что в отличие от сквидов, сигнальная характеристика криозондового магнитометра не является периодической, поэтому такой магнитометр может измерять абсолютное значение магнитной индукции, а не только ее изменение.
5. Заключение
1. Получено приближенное решение задачи о нелинейном взаимодействии взаимно-перпендикулярных магнитных полей в сверхпроводнике второго рода в квазистационарном приближении.
2. Показана возможность использования взаимодействия взаимно-перпендикулярных магнитных поле в сверхпроводящей проволоке для измерения напряженности магнитного поля.
3. Оценена предельная чувствительность криозондового магнитометра с поперечным возбуждением, рекордная даже для квантовых магнитометров.
Работа выполнена в рамках реализации ФПЦ «Научные и научно-педагогические кадры инновационной Росии» на 2009 – 2013 годы (соглашение № 14.В37.21.0736).
6. Список литературы
1. Горелик Г.С. О некоторых нелинейных явлениях, происходящих при суперпозиции взаимно перпендикулярных магнитных полей // Известия Академии наук СССР. Серия Физическая. 1944. Т. VIII, № 4. С. 172-188.
2. Зацепин Н.Н. Метод высших гармоник в неразрушающем контроле металлов. Минск: Наука и техника, 1980. 167 с.
3. Афанасьев Ю.В. Феррозонды. Л.: Энергия, 1969. 168 с.
4. Гинзбург В.Л., Ландау Л.Д. К теории сверхпроводимости // Журнал экспериментальной и теоретической физики. 1950. Т. 20, вып. 12. С. 1064 – 1082.
5. Игнатьев В.К. Обобщенная проницаемость сверхпроводника второго рода // Физика низких температур. 2005. Т. 31, № 12. С. 1355 – 1365
6. Игнатьев В.К., Черных С.В. Сверхпроводящий магнитометр с обратной связью по магнитному полю // Приборы и техника эксперимента. 1996. № 2. С. 124 - 126.
7. Игнатьев В.К., Якимец А.Л. ВТСП-магнитометр с двойной модуляцией // Измерительная техника. 2000. № 10. С. 49 - 52.
8. Игнатьев В.К., Якимец А.Л. Нелинейное взаимодействие трех волн в проводящем магнетике // Физика волновых процессов и радиотехнические системы. 2002. № 1. С. 55 - 59
9. Алфеев В.Н., Бахтин П.А., Васенков А.А., Войтович И. Д., Махов В. И. Интегральные схемы и микроэлектронные устройства на сверхпроводниках / Под ред. В.Н. Алфеева. М.: Радио и связь, 1985. 232 с.
10. Игнатьев В.К., Краснополин И.Я. Оптимизированный СКВИД с радиочастотным смещением в диапазоне 25 - 30 МГц // Приборы и техника эксперимента. 1982. № 1. С. 198 – 201.
11. Зайцев В.Ф., Полянин А.Д. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 2001. 576 с.
12. Шмидт В.В. Введение в физику сверхпроводников. М.: МЦНМО, 2000. 402 с.
13. Копелевич Я.В., Леманов В.В., Холкин А.Л.. Частотная зависимость импеданса и глубина проникновения магнитного поля в керамике ![]() // Физика твердого тела. 1989. Т. 31, вып. 8. С. 302 – 304.
// Физика твердого тела. 1989. Т. 31, вып. 8. С. 302 – 304.
Публикации с ключевыми словами: сверхпроводник, магнитометр, СКВИД, криотрон, скрещенные магнитные поля, нелинейный магнетик
Публикации со словами: сверхпроводник, магнитометр, СКВИД, криотрон, скрещенные магнитные поля, нелинейный магнетик
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



