научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2012
DOI: 10.7463/0912.0475444
УДК: 621.396.662
Россия, МГТУ им. Н.Э. Баумана
Введение
Помехоустойчивость систем синхронизации до недавнего времени исследовалась лишь при шумовом воздействии [1-3].
С развитием радиотехники, систем связи и космической радионавигации возникла необходимость исследовать системы синхронизации не только при шумовых воздействиях, но и при комбинированных воздействиях, состоящих из аддитивной смеси сигнала, гармонической помехи и шума.
Работы, посвящённые анализу статистических характеристик системы синхронизации при комбинированных воздействиях, исчисляются до настоящего времени единицами [4-5]. В этих работах рассматриваются, как правило, воздействия на ФАП 1-го порядка [6], причём, сами статистические характеристики, получаемые для разных типов ФАП, не сравниваются между собой.
Проведен анализ статистической динамики непрерывных систем фазовой автоподстройки (ФАП) 2-го порядка при наличии гармонической помехи. На основе аппарата марковских случайных процессов (уравнения Фокера-Планка-Колмогорова (ФПК)) путём использования различных приближений получены статистические характеристики фазовой автоподстройки частоты 2-го порядка. В первую очередь это плотность распределения вероятности (ПРВ) сигнала рассогласования, частота срывов синхронизации, а также средняя разность между колебаниями управляемого генератора и сигнала при комбинированном воздействии на вход ФАП в виде аддитивной смеси сигнала, суммы нескольких гармонических помех и гауссова шума. Приведено сравнение характеристик ФАП 1-го и 2-го порядков.
1. Стохастическая модель системы
Рассмотрим воздействие одной гармоники совместно с шумом, когда частота помехи находится за полосой синхронизации.
Запишем стохастическое дифференциальное уравнение (ДУ) в виде
 (1)
(1)
где z(t) - сигнал ошибки; N(t) - низкочастотный шум; R – отношение помеха/сигнал (ОПС), F(p) - передаточная функция, p = d/dt.
Данное уравнение описывает изменение во времени усредненной во времени фазовой ошибки (или детерминированной составляющей фазовой ошибки) при одновременном воздействии на систему синхронизации широкополосного шума и узкополосной помехи, частота которой лежит за пределами полосы синхронизации.
На рис. 1 изображены зависимости от времени решений z(t) в системе второго порядка K=S=1; R=1, d=4; ![]() =0,5; отношение сигнал/шум (ОСШ) r=30 дБ. В этом случае,
=0,5; отношение сигнал/шум (ОСШ) r=30 дБ. В этом случае,  . АЧХ и ФЧХ фильтра имеют вид
. АЧХ и ФЧХ фильтра имеют вид 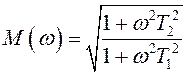 ,
, ![]() .
.
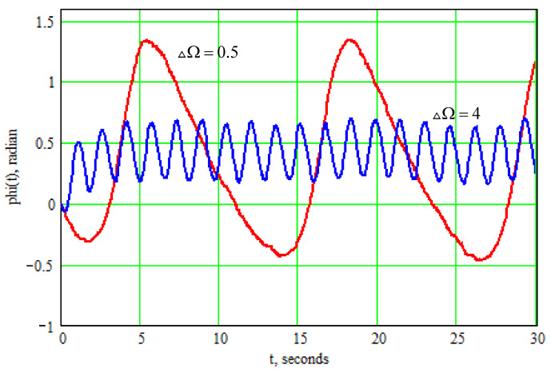
Рисунок 1 - Траектория фазовой ошибки для ФАП второго порядка
2. Анализ стохастической системы ФАП второго порядка
Запишем уравнение ФПК в виде
 (2)
(2)
где ![]()
В установившемся режиме, полагая  0, по (2) получим обыкновенное дифференциальное уравнение второго порядка
0, по (2) получим обыкновенное дифференциальное уравнение второго порядка
 (3)
(3)
с граничным условием ![]()
ДУ (2) запишем в виде
 (4)
(4)
По определению П(x) – поток вероятности, а условие ![]() означает стационарность потока вероятности. Решение ДУ имеет вид
означает стационарность потока вероятности. Решение ДУ имеет вид

где 
Постоянные ![]() и
и ![]() найдем из условий
найдем из условий

где границы ![]() и
и ![]() интервала
интервала ![]() таковы, что
таковы, что ![]()
В результате получим

Из условия равенства ![]() выразим
выразим ![]() через
через ![]() , т.е.
, т.е.
![]()
где 
Таким образом, ПРВ ![]() можно записать в виде
можно записать в виде

где 

Отсюда при ![]() после преобразования находим
после преобразования находим
 (5)
(5)
Здесь
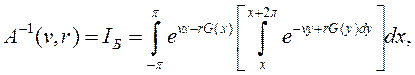 (6)
(6)
где 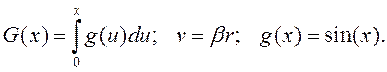
На рис. 2а представлен график зависимости ПРВ ![]() ФАП второго порядка, рассчитанной по формуле (5) при r=16 и разных значениях
ФАП второго порядка, рассчитанной по формуле (5) при r=16 и разных значениях ![]() : 1 -
: 1 - ![]() =0.2; 2 -
=0.2; 2 - ![]() =0.4; 3 -
=0.4; 3 - ![]() =0.6; 4 -
=0.6; 4 - ![]() =0.8; 5 -
=0.8; 5 - ![]() =0.9; 6 -
=0.9; 6 - ![]() 1. На рис. 2б: 1-
1. На рис. 2б: 1- ![]() -0.4; 2 -
-0.4; 2 - ![]() 0.4; 3 -
0.4; 3 - ![]() -0.6; 4 -
-0.6; 4 - ![]() 0.6; 5 -
0.6; 5 - ![]() -0.8; 6 -
-0.8; 6 - ![]() 0.8.
0.8.

Рисунок 2 – ПРВ ![]() : а) ФАП второго порядка; б) ФАП первого порядка при r=8; d=1,5;
: а) ФАП второго порядка; б) ФАП первого порядка при r=8; d=1,5; ![]() =0,4.
=0,4.
![]() ,
,  ,
, 
Среднее время до срыва слежения имеет вид [7]
![]() (7)
(7)
где 
![]()
 .
.
На рис. 3а построен график зависимости ![]() от ОСШ ФАП второго порядка, рассчитанный по (7) при разных значениях а: 1 - а=0.2; 2 - а=0.4; 3 - а=0.6; 4 - а=0.8. На рис. 3б построен график зависимости
от ОСШ ФАП второго порядка, рассчитанный по (7) при разных значениях а: 1 - а=0.2; 2 - а=0.4; 3 - а=0.6; 4 - а=0.8. На рис. 3б построен график зависимости ![]() ФАП первого порядка: 1 -
ФАП первого порядка: 1 - ![]() =0.4; 2 -
=0.4; 2 - ![]() =0.6; 3 -
=0.6; 3 - ![]() =0.8; 4 -
=0.8; 4 - ![]() =0.9.
=0.9.
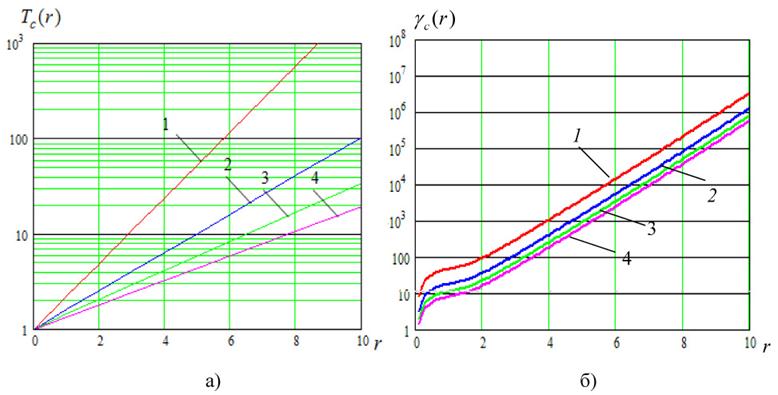
Рисунок 3 – Зависимость среднего времени до срыва слежения ![]() от ОСШ:
от ОСШ:
а) ФАП второго порядка при ![]() ; б) ФАП первого порядка при d=1.5,
; б) ФАП первого порядка при d=1.5, ![]() 0.3
0.3
Найдем среднее значение частотного рассогласования. Можно показать, что справедливо соотношение [7]
 , (8)
, (8)
где ![]() - среднее значение частотного рассогласования между частотой сигнала и частотой управляемого генератора.
- среднее значение частотного рассогласования между частотой сигнала и частотой управляемого генератора.
На рис. 4 а,б даны графики зависимостей![]() ФАП второго и первого порядка при
ФАП второго и первого порядка при ![]() = var. На рис. 4а: 1 -
= var. На рис. 4а: 1 - ![]() =0.2; 2 -
=0.2; 2 - ![]() =0.4; 3 -
=0.4; 3 - ![]() =0.6; 4 -
=0.6; 4 - ![]() =0.8; 5 -
=0.8; 5 - ![]() =0.9. На рис. 4б: 1 -
=0.9. На рис. 4б: 1 -![]() =0; 2 -
=0; 2 - ![]() =0.2; 3 -
=0.2; 3 - ![]() =0.4; 4 -
=0.4; 4 - ![]() =0.6.
=0.6.

Рисунок 4 – Зависимость частотной расстройки ![]() от ОСШ r: а) ФАП второго порядка; б) ФАП первого порядка при d=0,5,
от ОСШ r: а) ФАП второго порядка; б) ФАП первого порядка при d=0,5,![]() 0,5.
0,5.
По результатам анализа графиков можно сделать следующие выводы.
1) При увеличении значения частотной расстройки ![]() значение ПРВ W(x) уменьшается. Для ФАП первого порядка эта тенденция более выражена, чем для ФАП второго порядка.
значение ПРВ W(x) уменьшается. Для ФАП первого порядка эта тенденция более выражена, чем для ФАП второго порядка.
2) С ростом значения частотной расстройки ![]() уменьшается значение среднего времени до срыва слежения
уменьшается значение среднего времени до срыва слежения ![]() для всех значений ОСШ. Для ФАП второго порядка эта тенденция более выражена, чем для ФАП первого порядка.
для всех значений ОСШ. Для ФАП второго порядка эта тенденция более выражена, чем для ФАП первого порядка.
3) Увеличение значения частотной расстройки ![]() приводит к росту среднего значения частотного рассогласования
приводит к росту среднего значения частотного рассогласования ![]() . Для ФАП второго порядка эта тенденция более выражена, чем для ФАП первого порядка.
. Для ФАП второго порядка эта тенденция более выражена, чем для ФАП первого порядка.
Список литературы
1. Тихонов В.И. Влияние шумов на работу схемы фазовой автоподстройки частоты // Автоматика и телемеханика. 1959. № 9. С. 1188-1196.
2. Шахтарин Б.И. Анализ асимптотических значений статистических характеристик системы ФАПЧ // Радиотехника и электроника. 1986. № 2. С. 246-258.
3. Линдсей В. Системы синхронизации в связи и управлении: Пер. с англ. / Под ред. Ю.Н. Бакаева и М.В. Капранова. М.: Сов. Радио, 1978. 600 с.
4. Шахтарин Б.И. Статистическая динамика систем синхронизации. М.: Радио и связь, 1998. 488 с.
5. Karsi M.F., Lindsey W.C. Effects of CW interference on carrier tracking // Proc. of the Military Communications Conference MILCOM '94. IEEE, 1994. P. 301-305. DOI: http://dx.doi.org/10.1109/MILCOM.1994.473923
6. Ковальчук А. А., Сидоркина Ю. А., Рязанова М. А. Воздействие на систему синхронизации гармонических помех и шума // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2011. № 3. Режим доступа: http://technomag.edu.ru/doc/169529.html (дата обращения 19.10.2012).
7. Шахтарин Б.И. Анализ систем синхронизации при наличии помех. М.: ИПРЖР, 1996. 252 с.
Публикации с ключевыми словами: частотное рассогласование, срыв слежения, гармоническая помеха, плотность распределения вероятностей, ФАП второго порядка, аддитивный шум, полоса синхронизации
Публикации со словами: частотное рассогласование, срыв слежения, гармоническая помеха, плотность распределения вероятностей, ФАП второго порядка, аддитивный шум, полоса синхронизации
Смотри также:
- 77-30569/296014 Среднее время до срыва слежения и среднее значение частотного рассогласования фазовой автоподстройки при наличии комбинированного воздействия
- 77-48211/359541 Статистическая динамика фазовой автоподстройки второго порядка при воздействии комбинированных помех
- 77-30569/353914 Оценка действия гармонической помехи на фазовую автоподстройку
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



