научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2012
DOI: 10.7463/0812.0475421
УДК: 621.396.662
Россия, МГТУ им. Н.Э. Баумана
Введение
Теория стохастических систем фазовой автоподстройки (ФАП) начала формироваться работами Р.Л. Стратоновича [1] и В.И. Тихонова. Одним из основных методов исследования является метод марковских и полумарковских случайных процессов и цепей, разработанные А.Н. Колмогоровым и Л.С. Понтрягиным [2]; применяются интегральное уравнение Колмогорова-Чепмена и уравнение среднего времени до срыва синхронизации (работы Ч. Цзы [3], А. Вайнберг и В. Ли [4], В.И. Витюцкого и В.Н. Сердюкова [5]). В указанных работах найдены плотности распределения вероятности (ПРВ) координат, в меньшей степени исследованы характеристики срыва слежения, причем рассмотрены детерминированные системы, и не проводится анализ стохастической системы. Так же среди систем ФАП особое внимание уделяется непрерывным системам [6], а статистические характеристики дискретных ФАП до сих пор исследованы в меньшей степени, отчасти в силу многообразия дискретных систем.
В данной статье приводится анализ стохастической дискретной ФАП при синусоидальной характеристики детектора. Приводятся зависимости стационарных ПРВ при нулевой частотной расстройке, рассчитанные методом Галеркина. Приведен приближенный метод вычисления ПРВ на основе метода Галёркина. Сопоставлены результаты точных и приближенных методов. Делается вывод о том, что система алгебраических уравнений, полученная методом расщепления ядра интегрального уравнения, имеет тот же вид, что и система, полученная методом Галёркина. Приводятся графики нестационарной ПРВ при равномерном начальном распределении. Исследованы моменты времени до срыва слежения в дискретной ФАП. Приводятся зависимости среднего значения времени до срыва слежения от отношения сигнал/шум. В результате показаны основные статистические характеристики плотности вероятностей фазового рассогласования в стационарном и нестационарном режимах работы, времени до срыва слежения в импульсных фазовых системах.
1. Анализ стохастической дискретной ФАП при синусоидальной характеристике детектора
Рассмотрим статистическую динамику дискретной ФАП при синусоидальной характеристике детектора ![]() . Разностное уравнение ФАП в этом случае принимает вид
. Разностное уравнение ФАП в этом случае принимает вид
![]() (1)
(1)
причем среднее значение равно
![]() ,
,
где ![]() - период,
- период, ![]() - частотная растройка,
- частотная растройка, ![]() - гауссова последовательность.
- гауссова последовательность.
Уравнение Колмогорова-Чепмена запишем в виде [7]
 (2)
(2)
где
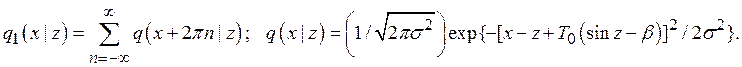
В стационарном режиме уравнение Колмогорова-Чепмена переходит в интегральное уравнение Фредгольма второго рода
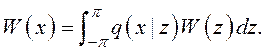
Предположим, что, как и в случае непрерывной системы при ![]() , сигнал рассогласования в стационарном режиме распределен по закону Тихонова [8] при
, сигнал рассогласования в стационарном режиме распределен по закону Тихонова [8] при ![]() , где
, где ![]() Тогда
Тогда
 (3)
(3)
где ![]() - функция Бесселя.
- функция Бесселя.
Рассмотрим влияние интервала дискретизации сигнала на плотность распределения вероятности (ПРВ) ![]() . Вычисление интеграла в правой части уравнения Колмогорова-Чепмена проведем при
. Вычисление интеграла в правой части уравнения Колмогорова-Чепмена проведем при ![]() и
и ![]() Для сравнения с [7] составим перечень значений отношения сигнал/шум
Для сравнения с [7] составим перечень значений отношения сигнал/шум ![]() где
где ![]() Пусть
Пусть ![]() тогда значениям
тогда значениям ![]() соответствуют
соответствуют ![]() и
и ![]() При
При ![]() для тех же значений
для тех же значений ![]() имеем
имеем ![]() и
и ![]() (рис. 1).
(рис. 1).
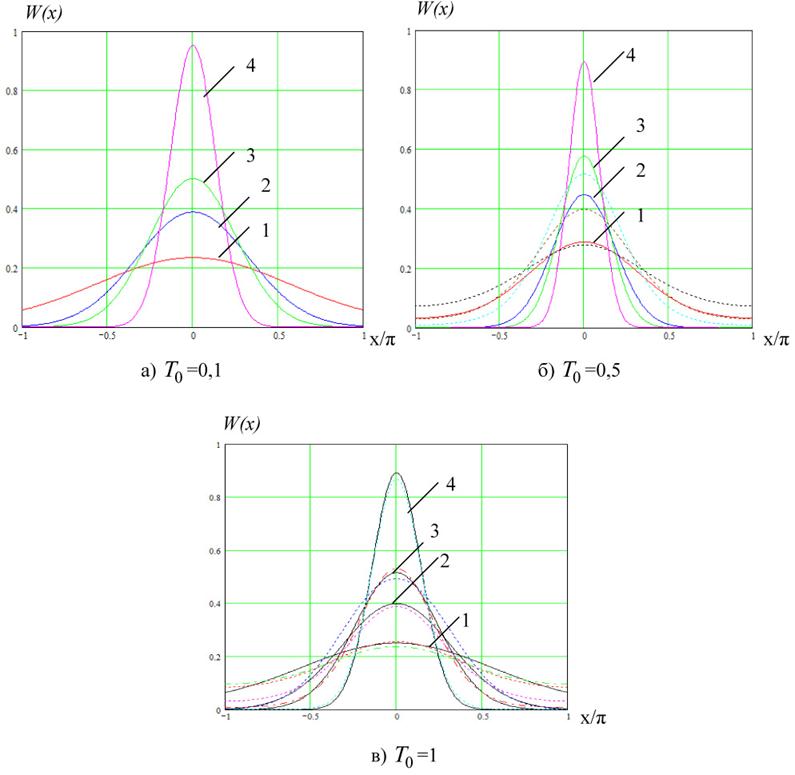
Рисунок 1 – Cтационарная ПРВ ![]() при
при ![]() и различных значениях
и различных значениях ![]()
Результаты сравнения видны на рис.1 а-в, где приведены зависимости стационарных ПРВ ![]() от x при
от x при ![]() и значениях
и значениях ![]() , равных 0,1; 0,5; 1. Сплошными линиями обозначены результаты расчета методом Галеркина, штриховыми линиями – ПРВ
, равных 0,1; 0,5; 1. Сплошными линиями обозначены результаты расчета методом Галеркина, штриховыми линиями – ПРВ ![]() (3) непрерывной системы.
(3) непрерывной системы.
2. Вычисление статистических характеристик ФАП приближенным методом
Рассмотрим приближенный метод вычисления ПРВ ![]() на основе метода Галёркина [8]. Пусть
на основе метода Галёркина [8]. Пусть

где {![]() } (n=0,1…) – полная система ортогональных на интервале
} (n=0,1…) – полная система ортогональных на интервале ![]() функций.
функций.
Точное значение ПРВ находим в форме предельного соотношения
![]()
Тогда
 (4)
(4)
где ![]()
![]() - расчетные коэффициенты.
- расчетные коэффициенты.
Приведенные соотношения для коэффициентов ряда (4) могут быть получены методом замены ядра интегрального уравнения Колмогорова-Чепмена на вырожденное разложение ядра ![]() в двойной ряд Фурье.
в двойной ряд Фурье.
Рассмотрим анализ нестационарного режима методом Галёркина. Плотность распределения вероятности
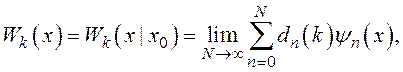
где ![]() - начальное значение фазового рассогласования.
- начальное значение фазового рассогласования.
Согласно уравнения Колмогорова-Чепмена и условию ![]() имеем
имеем ![]() Отсюда
Отсюда 
Подставляя ряд для функции ![]() в интегральное уравнение (2), получаем выражение
в интегральное уравнение (2), получаем выражение

где

 (5)
(5)
В частном случае ![]() выражение для стационарной ПРВ сигнала рассогласования в дискретной системе принимает вид
выражение для стационарной ПРВ сигнала рассогласования в дискретной системе принимает вид
 (6)
(6)
Ограничимся первым слагаемым ряда (6). Тогда
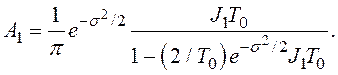
Результаты расчета ПРВ W(x) приведены сплошными линиями на рис. 1 а-в. На рис. 2 и рис. 4 изображены графики при ![]() . На рис. 2 изображены графики ПРВ при
. На рис. 2 изображены графики ПРВ при![]() ,
, ![]()
![]() (1);
(1); ![]() (2);
(2); ![]() (3); штриховой линией отмечена ПРВ для непрерывной системы. На рис. 3 изображены графики нестационарной ПРВ при равномерном начальном распределении
(3); штриховой линией отмечена ПРВ для непрерывной системы. На рис. 3 изображены графики нестационарной ПРВ при равномерном начальном распределении ![]() когда
когда ![]() t=1 (1), t=2 (2),t=4 (3), t=10 (4); штриховой линией отмечена ПРВ для непрерывной системы. На рис. 4 а,б принято, что
t=1 (1), t=2 (2),t=4 (3), t=10 (4); штриховой линией отмечена ПРВ для непрерывной системы. На рис. 4 а,б принято, что ![]() (1);
(1); ![]() (2);
(2); ![]() (3);
(3); ![]() (4). На рис. 4 а:
(4). На рис. 4 а: ![]() ; на рис. 4 б:
; на рис. 4 б: ![]() .
.
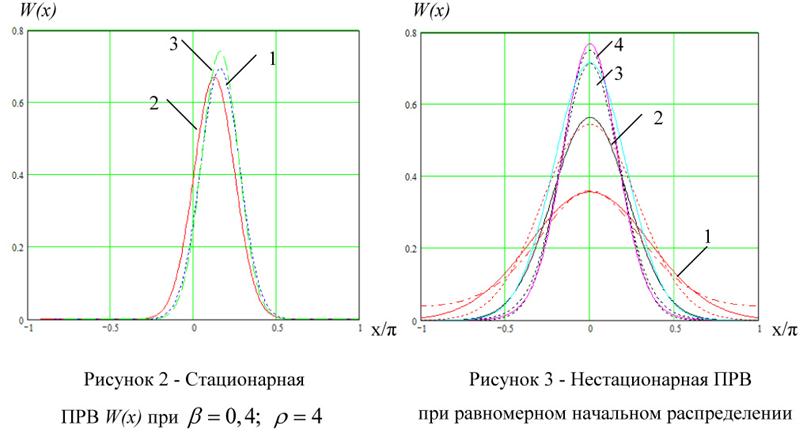

Рисунок 4 – ПРВ W(x) при ![]()
3. Моменты времени до срыва слежения в дискретной ФАП
Для вероятности срыва слежения на i-м шаге можно записать [9] в виде
 (7)
(7)
Определим k-й начальный момент числа шагов до срыва синхронизации ![]()

Получаем рекуррентные соотношения для начальных моментов числа шагов до срыва синхронизации
 (8)
(8)
где ![]() - биномиальный коэффициент,
- биномиальный коэффициент, 
Для решения интегрального уравнения (8) использовался метод квадратур, основанный на использовании формулы Гаусса для приближенного вычисления определенного интеграла.
На рис. 5 приведены зависимости среднего значения времени ![]() до срыва слежения при
до срыва слежения при ![]() и различных значениях
и различных значениях ![]() и
и ![]() : (1) -
: (1) - ![]() =0; (2) -
=0; (2) - ![]() =0,1; (3) -
=0,1; (3) - ![]() =0,5; (4) -
=0,5; (4) -![]() =1 (штриховой линией отмечены данные из [10]).
=1 (штриховой линией отмечены данные из [10]).
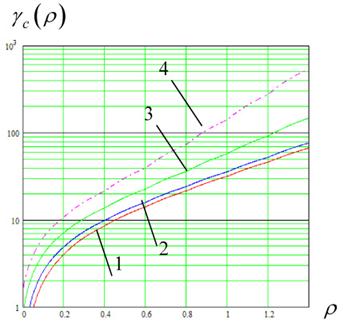
Рисунок 5 - Cреднее значение времени до срыва слежения ![]() при
при ![]()
Заключение
Проведен анализ стохастической дискретной ФАП при синусоидальной характеристики детектора. Приведены зависимости стационарных ПРВ ![]() при
при ![]() , рассчитанные методом Галеркина. Рассмотрен приближенный метод вычисления ПРВ W(x) на основе метода Галёркина. Сделан вывод о том, что система алгебраических уравнений, полученная методом расщепления ядра интегрального уравнения, имеет тот же вид, что и система, полученная методом Галёркина. Приведены графики нестационарной ПРВ при равномерном начальном распределении
, рассчитанные методом Галеркина. Рассмотрен приближенный метод вычисления ПРВ W(x) на основе метода Галёркина. Сделан вывод о том, что система алгебраических уравнений, полученная методом расщепления ядра интегрального уравнения, имеет тот же вид, что и система, полученная методом Галёркина. Приведены графики нестационарной ПРВ при равномерном начальном распределении ![]() . Исследованы моменты времени до срыва слежения в дискретной ФАП. Приведены зависимости среднего значения времени до срыва слежения
. Исследованы моменты времени до срыва слежения в дискретной ФАП. Приведены зависимости среднего значения времени до срыва слежения ![]() от
от ![]() .
.
Список литературы
1. Стратонович Р.Л. Избранные вопросы теории флуктуации в радиотехнике. М.: Советское радио, 1961. 210 с.
2. Андронов В.А., Витт А.А., Понтрягин Л.С. О статистическом рассмотрении динамических систем // Журнал Экспериментальной и Теоретической Физики (ЖЭТФ). 1933. Т. 3, № 3. С. 165-180.
3. Chie C.M. Mathematical analogies between first-order digital and analog phase-locked loops // IEEE Trans. on Communications. 1978. Vol. COM-26, № 6. P. 860-865. DOI: 10.1109/TCOM.1978.1094148
4. Weinberg A., Liu B. Discrete time analysis of nonuniform sampling first- and second- order phase-locked loops // IEEE Trans. on Communications ,1974. Vol. COM-22, № 2. P. 123-137. DOI: 10.1109/TCOM.1974.1092168
5. Битюцкий В.И., Сердюков П.Н. Оценка времени до срыва синхронизма в импульсной системе ФАПЧ // Радиотехника. 1973. № 8. С. 95-97.
6. Ковальчук А. А., Сидоркина Ю. А., Рязанова М. А. Воздействие на систему синхронизации гармонических помех и шума // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2011. № 3. Режим доступа: http://technomag.edu.ru/doc/169529.html (дата обращения 19.10.2012).
7. Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. М.-Л.: Гостехиздат, 1949. 695 с.
8. Шахтарин Б.И. Анализ кусочно-линейных систем с фазовым регулированием. М.: Машиностроение, 1990. 192 с.
9. Шахтарин Б.И., Сизых В.В., Курочка Б.Я. Исследование статистических характеристик дискретных ФАС первого порядка // Вестник МГТУ. Сер. Приборостроение. 1992. №3. С. 89-110.
10. Первозванский А.А. Случайные процессы в нелинейных автоматических системах. М.: Наука, 1962. 352 с.
Публикации с ключевыми словами: метод марковских случайных процессов, срыв слежения, дискретные системы фазовой синхронизации, синусоидальная характеристика детектора, плотности вероятностей фазового рассогласования, метода Галёркина
Публикации со словами: метод марковских случайных процессов, срыв слежения, дискретные системы фазовой синхронизации, синусоидальная характеристика детектора, плотности вероятностей фазового рассогласования, метода Галёркина
Смотри также:
- 77-48211/359541 Статистическая динамика фазовой автоподстройки второго порядка при воздействии комбинированных помех
- 77-30569/296014 Среднее время до срыва слежения и среднее значение частотного рассогласования фазовой автоподстройки при наличии комбинированного воздействия
- Воздействие на ФАП второго порядка гармонической помехи и аддитивного шума
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



