научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#11 ноябрь 2004
А.В. Аграновский, канд. техн. наук,
Д.А. Леднов, ГП КБ “СПЕЦВУЗАВТОМАТИКА” г. Ростов-на-Дону
Математическая модель распознавания речи с использованием протяженных контекстов
Обсуждается математическая модель распознавания речи с использованием протяженных текстов. Показано, что введение операции перенормировки Марковской матрицы переходов между состояниями позволяет ввести зависимость принимаемых решений от контекста. Данная операция оказывается равносильной введению в систему обратных связей.
ВВЕДЕНИЕ
На протяжении последних лет в области распознавания речи пользуются популярностью скрытые модели Маркова (НММ) [1-3], построенные на базе математического формализма однородных цепей Маркова, и иерархические композиционные модели, основанные на теории оптимальных решений - динамическом программировании (ИКДП - подход) [4, 5].
В работе [6] проведено сравнение этих двух типов моделей и найдены их основные сходства и различия. В добавление к этому анализу необходимо отметить, что обе модели несут в себе ограничение, которое заключено в зависимости вероятности состояния в момент времени t лишь от предшествующего состояния в момент времени t-1.
В НММ такое ограничение очевидно, оно связано с условием марковской цепи
![]()
где ![]() — условная
вероятность события S(t)
после события S(t-1);
t — дискретное время. Здесь отсутствует
зависимость условной вероятности состояния S(t) от всей предшествующей динамики состояний.
— условная
вероятность события S(t)
после события S(t-1);
t — дискретное время. Здесь отсутствует
зависимость условной вероятности состояния S(t) от всей предшествующей динамики состояний.
В ИКДП - подходе накладываются ограничения на возможный порядок следования состояний, т.е. указываются те состояния S(t), в которые можно попасть из состояния S(t-1), что опять же равносильно ограничению, подобному (1).
Введем некоторые определения, необходимые для дальнейшего изложения.
Зависимость условной вероятности события S(t) от предшествующих событий S(t-1),..., S(t-m), где m<1будем называть контекстной зависимостью.
Ограниченную временную последовательность событий {S(t-1), S(t-2),…, S(t-m)} будем называть контекстом, а число m - мерой контекстной зависимости.
Очевидно, что с точки зрения данных определений мера контекстной зависимости НММ и ИКДП - подхода равна 1.
В названии статьи мы употребили термин протяженные контексты в том смысле, что в настоящей работе будет идти речь о возможностях построения моделей с мерой контекстной зависимости более единицы.
ОПИСАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Поставим задачу распознавания речи формально. Пусть имеется алфавит F, состоящий из N
различных фонем F:{Si}
(для удобства в дальнейшем Si будем
называть состоянием). Состояния различны в том смысле, что существует оператор
сравнения ![]() ,
подчиняющийся условиям
,
подчиняющийся условиям

где g << 1 — некоторое число (параметр модели).
Пусть имеется словарь W, состоящий из М различных транскрипций слов. Каждая транскрипция - это последовательность номеров фонем r, полученных из реализаций слов
![]()
где j - номер транскрипции в словаре; Li - длина j-й транскрипции.
В результате предварительной обработки речевого сигнала образуется бесконечная последовательность состояний X:{х1,..., хt, хt+1,..}.
Суть задачи распознавания состоит в том, чтобы поставить в соответствие подпоследовательности X' последовательности X соответствующую транскрипцию словаря W.
Рассмотрим, как эта задача решается с помощью неоднородных цепей Маркова.
Прежде всего, обратимся к процедуре обучения. Процедура обучения состоит в следующем:
1) сегментирование раздельно произнесенных слов спектральным окном фиксированного размера Т0 со смещением во времени t, как правило, Т0 > t (два последовательно взятых спектральных окна пересекаются);
2) получение в каждом окне спектральной оценки одним из известных способов [7];
3) сглаживание спектральной оценки и выделение формант (образование состояний S(t), несущих информацию о частотах и интенсивностях формант);
4) сравнение двух последовательно взятых состояний S(t) и S(t-1), которое есть не что иное, как корреляция между состояниями:
 (1)
(1)
где ωi - дискретная частота спектральной оценки; t - дискретное время. При выполнении условия ![]() состояния S(t) и S(t-1) предполагаются различными, в противном случае состояния
предполагаются одинаковыми;
состояния S(t) и S(t-1) предполагаются различными, в противном случае состояния
предполагаются одинаковыми;
5) запись различных состояний в алфавит фонем F;
6) получение матрицы вероятностей переходов из одного состояния в другое
на всем множестве обучающей выборки слов с размерностью Ms.
Для этого необходимо найти частоту встречи реализации события ![]() такого, что за
состоянием Sj(t-1)
следует состояние Si(t), где i, j - номера состояний (нулевой
отсчет времени соответствует началу слова). Заметим, что возможны ситуации,
когда: а) для наблюдаемого состояния j существуют такие состояния, в которые на всем множестве
обучающей выборки слов не наблюдалось ни одного перехода — все такие состояния
будем считать равновероятными; б) само состояние j
является ненаблюдаемым. Переходы из состояния j в состояние i для всех i будем считать
равновероятными.
такого, что за
состоянием Sj(t-1)
следует состояние Si(t), где i, j - номера состояний (нулевой
отсчет времени соответствует началу слова). Заметим, что возможны ситуации,
когда: а) для наблюдаемого состояния j существуют такие состояния, в которые на всем множестве
обучающей выборки слов не наблюдалось ни одного перехода — все такие состояния
будем считать равновероятными; б) само состояние j
является ненаблюдаемым. Переходы из состояния j в состояние i для всех i будем считать
равновероятными.
Из этих соображений запишем матрицу вероятностей в виде
 (2)
(2)
где М0 — число состояний, переход в которые из состояния j не наблюдался.
Далее рассмотрим процедуру распознавания. Вероятность того, что подпоследовательность X' соответствует j-й транскрипции словаря W, определяется следующим выражением:
![]() (3)
(3)
где t0 - абсолютное время появления входного
речевого сигнала; вероятность ![]() характеризует величину сходства
входного паттерна x и состояния Si а ее вычисление равносильно вычислению
корреляции (1), нормированной на сумму корреляций со всевозможными состояниями
из алфавита фонем F, т.е.
характеризует величину сходства
входного паттерна x и состояния Si а ее вычисление равносильно вычислению
корреляции (1), нормированной на сумму корреляций со всевозможными состояниями
из алфавита фонем F, т.е.
 (4)
(4)
Окончательное решение о распознавании слова принимается с помощью операции максимизации по всевозможным транскрипциям, и вычислению индекса максимально вероятной транскрипции G:
![]() (5)
(5)
Предположим, что в рамках вероятностного подхода, частными случаями которого являются НММ и ИКДП, мы хотим увеличить размерность используемого контекста.
Для этого допустим, что определены компоненты матриц
![]()
и
![]()
тогда выражение, определяющее вероятность соответствия подпоследовательности X' и j-й транскрипции словаря W, примет форму
 (6)
(6)
Очевидно, что в рамках вероятностного подхода существует принципиальная
возможность и дальнейшего увеличения контекста. Однако требование a priori
знать значения компонент матрицы Vijk(t), а при дальнейшем увеличении контекста - и компонент
матриц более высокого порядка сделает процедуру обучения сложной. Рост числа
операций сложения и умножения Nn, где
n - размерность контекста, которые затрачиваются
на вычисление вероятности ![]() , делает стандартный вероятностный
подход практически неприемлемым.
, делает стандартный вероятностный
подход практически неприемлемым.
Рассмотрим другой подход. Вернемся к модели неоднородных цепей Маркова. Значение вероятности pi(t) того, что система в момент времени t находится в состоянии Si(t), определяется выражением
![]() (7)
(7)
Введем понятие вероятного события. Будем говорить, что если pi(t) > Q, где Q - порог, 0<Q<1, то событие является вероятным, иначе событие является невероятным.
Таким образом, множество значений вероятностей {pi(t)} в момент времени t разбивается на два подмножества:
а) подмножество вероятных событий, назовем его ρ;
б) подмножество невероятных событий, назовем его Θ.
Допустим, что в каждый отсчет дискретного времени в интервале 0,..., t,..., Т среди прочих последовательностей
вероятностей была получена временная последовательность ![]() такая, что
такая, что ![]() для любого t и последовательность значений номеров {it} совпадает с подпоследовательностью,
записанной в одной из транскрипций словаря W,
для определенности пусть это будет k-я транскрипция.
для любого t и последовательность значений номеров {it} совпадает с подпоследовательностью,
записанной в одной из транскрипций словаря W,
для определенности пусть это будет k-я транскрипция.
Нам необходимо учесть, что процесс длительное время развивается вдоль одной из существующих транскрипций. Для этого введем в модель (7) новую матрицу переходов Фij(t):
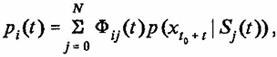 (8)
(8)
которую определим в виде
 (9)
(9)
где A - введенная эвристическая матрица. Операция (9) означает не что иное, как перенормировку матрицы переходов D(t) неоднородной цепи Маркова. Заметим, что выбор матрицы A(t) произволен, т.е. для любой матрицы A(t) будет удовлетворяться условие

накладываемое на матрицу переходов цепей Маркова. Для того чтобы убедиться в этом, достаточно просуммировать правую часть (9) по индексу i.
Поясним смысл введенной матрицы на примере структурной схемы устройства распознавания речи (см. рисунок).

Структурная схема устройства распознавания речи
На вход системы I подается
паттерн x(t).
Элементами первого слоя L1 на первом этапе
обработки определяются вероятности ![]() . На втором этапе обработки в L1 посредством матрицы D(t) (которую можно интерпретировать как матрицу связей
между элементами слоя) формируются выходные значения слоя, т.е. вероятности pi(t).
. На втором этапе обработки в L1 посредством матрицы D(t) (которую можно интерпретировать как матрицу связей
между элементами слоя) формируются выходные значения слоя, т.е. вероятности pi(t).
Поскольку мы использовали неоднородную модель и значения матрицы D(t) изменяются со временем, то в структурной схеме Z-слой отвечает за формирование связей между элементами слоя L1 в каждый момент времени.
Каждый элемент второго слоя L2 отвечает определенной транскрипции словаря W. При выполнении условий
pi(t)>Q и i=rj(t),
где rj(t) - номер
фонемы j-й транскрипции (номер элемента в слое L2) от элемента j слоя L2, возникает обратная связь с весом ![]() к Z-слою,
в результате влияния которой происходит перенормировка исходной матрицы D(t) для слоя L1.
к Z-слою,
в результате влияния которой происходит перенормировка исходной матрицы D(t) для слоя L1.
Таким образом, компоненты матрицы A(t) можно интерпретировать как опосредованные обратные связи от слоя L2 к слою L1.
Выберем матрицу A(t) в форме
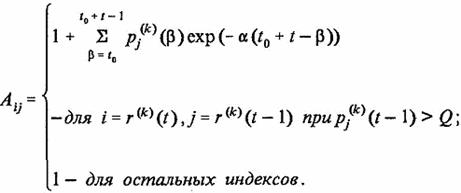 (10)
(10)
Оценим различия в поведении неоднородной цепи Маркова (3)-(5) и модели с перенормировками (8)-(10).
Для этого определим, каким условиям должен удовлетворять случайный процесс x(t) в момент t, чтобы он, вероятно, принадлежал транскрипции W. Очевидно, что для неоднородной цепи эти условия следующие [см. (7)]:
![]()
 (11)
(11)
Аналогичные условия можно получить для цепи с перенормировками [см. (8), (9)]:
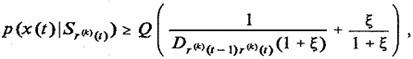 (12)
(12)
где ![]()
Отличие условия (11) от условия (12) заключается в том, что правая часть
(11), как функция времени, зависит лишь от изменения компонент матрицы
переходов, которые являются случайными величинами, а в правой части условия
(12) присутствует детерминированная функция ![]() (t),
расширяющая со временем область допустимых состояний, вероятных для данной
транскрипции.
(t),
расширяющая со временем область допустимых состояний, вероятных для данной
транскрипции.
* * *
Резюмируем рассуждения в виде указания последовательности выполняемых операций:
1) при обучении стандартным для НММ способом (2) получить матрицу переходов D;
2) на каждом такте дискретного времени определить множество вероятных событий ρ. Если вероятное событие принадлежит одной из транскрипций словаря, вычистить матрицу A (10);
3) перенормировать матрицу D (9) и получить новую матрицу Ф;
4) определить значение вероятности соответствия входного потока данных X одной из транскрипций словаря как

Список литературы
1. Bourlard H., Morgan N. Continuous speech recognition by connectionist statistical methods // IEEE TRANSACTIONS ON NEURAL NETWORKS. Vol. 4. № 6/November 1993.
2. Bahl L.R., Brown P.F., De Souza P.V., Mercer R.L., Picheny M.A. A Method for the construction of acoustic Markov models for words // IEEE TRANSACTIONS ON SPEECH AND AUDIO PROCESSING. Vol. l.N 4. October 1993.
3. Xucdong Huang, Kai-Fu Lee, On Speaker-Independent, Speaker-Dependent, and Speaker-Adaptive Speech Recognition. // IEEE TRANSACTIONS ON SPEECH AND AUDIO PROCESSING. Vol. 1. N 2. April 1993.
4. Винцюк Т.К. Анализ, распознавание и интерпретация речевых сигналов. Киев: Наукова Думка, 1987.
5. Винцюк Т.К. Организация вычислений при распознавании больших словарей // Автоматическое распознавание и синтез речевых сигналов: Сб. науч. тр. Киев, 1989.
6. Винцюк Т.К. Сравнение ИКДП- и НММ - методов распознавания речи // Методы и средства информ. речи. Киев, 1991.
7. Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения. М.: Мир, 1990
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ №7, 1997
ИНТЕЛЛКТУАЛЬНЫЕ СИСТЕМЫ
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



