научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2012
DOI: 10.7463/1012.0466325
УДК 621.313
Россия, МГТУ им. Н.Э. Баумана
Тактико-технические характеристики летательных аппаратов во многом зависят от качества инерциальных чувствительных элементов (ЧЭ) датчиков первичной информации (ДПИ) бортовых систем управления [1, 2]. В нашей стране и за рубежом усилился интерес разработчиков к использованию в системе чувствительных элементов прецизионных датчиков первичной информации управляемых магнитоэлектрических двигателей (МЭД) [3]. Управляемый магнитоэлектрический двигатель представляет собой электромеханическую систему, состоящую из синхронной электрической машины и силового электронного преобразователя (инвертора) – усилителя мощности, связанных между собой датчиком положения ротора. Датчик осуществляет позиционную обратную связь от ротора к инвертору. Такую систему еще называют бесконтактным двигателем постоянного тока (БДПТ) [4].
Для чувствительных элементов синхронная электрическая машина, которую в дальнейшем будем называть магнитоэлектрический двигатель, состоит из ротора с постоянными магнитами из редкоземельных материалов (для возбуждения) и безжелезного (диэлектрического) статора с обмоткой якоря. Интерес к магнитоэлектрическому двигателю для чувствительных элементов вызван его высоким (до 95 %), по сравнению с синхронным гистерезисным двигателем, КПД, а также возможностью устранения синхронных “качаний” ротора методами замкнутого регулирования и уменьшения пульсаций электромагнитных сил между ротором и статором за счет удаления “железа” со статора.
Высокая стабильность потребляемой мощности при стабилизированной скорости вращения ротора МЭД делает целесообразным использование для передачи энергии на чувствительный элемент бесконтактных трансформаторных токоподводов (ТТП) с ферромагнитными магнитопроводами. При этом стабильность мощности магнитоэлектрического двигателя обусловливает в свою очередь стабильность возмущающего момента тяжения, создаваемого ТТП. К тому же, основным и достаточно серьезным достоинством применения трансформаторных токоподводов является конструктивная законченность чувствительных элементов, позволяющая применить роботизированную сборку датчиков первичной информации в чистой камере без участия сборщика, исключив причины загрязнения внутренней среды прибора. Очевидно, что применение трансформаторных токоподводов создает определенную техническую проблему разгона МЭД частотным методом до полосы пропускания ТТП. Эта проблема нами успешно решена благодаря использованию специальных фазочувствительных выпрямителей, включенных во вторичный контур трансформаторных токоподводов, в номинальном режиме, шунтированных балластными сопротивлениями. На обмотки трансформаторных токоподводов питание подается с электронного преобразователя (ЭП) (рис. 1), в состав которого входят усилители
мощности (УМ).
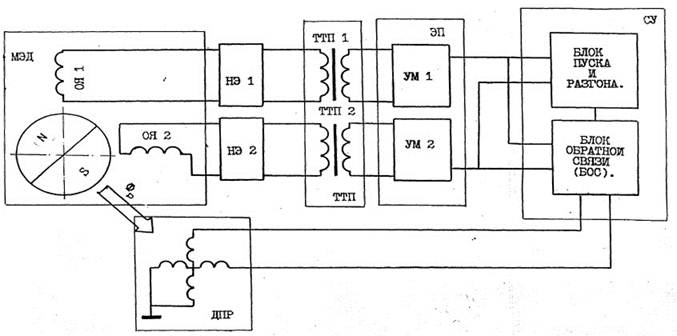
Рис. 1. Функциональная схема привода
Выше приведённые доводы являются обоснованием выбора магнитоэлектрического двигателя с трансформаторными токоподводами в системе чувствительных элементов.
В состав рассматриваемого привода входит также система управления (СУ), предназначенная для организации функционирования привода в режимах номинальной частоты вращения и разгона.
Очевидно, что качество чувствительных элементов определяется не только качеством системы управления, но и характеристиками элементов, входящих в состав ЧЭ и СУ. При проектировании МЭД - ТТП использован системный подход, который позволяет наилучшим образом согласовать элементы между собой и максимально использовать их потенциальные возможности по динамике и энергетике.
При анализе электромагнитных процессов в системе будем рассматривать МЭД как “идеальную” машину, у которой ЭДС вращения в фазах обмотки имеет синусоидальную форму, магнитная цепь не насыщена, между фазами обмотки отсутствует магнитная связь, поверхности статора и ротора — гладкие. Индуктивность обмотки можно не учитывать, так как она на двапорядка меньше индуктивности рассеяния вторичной обмотки ТТП из-за малой проницаемости материала магнитов. Для трансформаторных токоподводов цепь намагничивания в стационарном режиме замещаем линейной индуктивностью; активными потерями в магнитопроводе из феррита пренебрегаем, также пренебрегаем выпучиванием магнитного потока в зазоре и запасом энергии в электрических полях между слоями обмоток. Так как все электромагнитные расчеты, связанные с электромеханическим преобразованием энергии, будут проводиться для цепи вторичной обмотки ТТП, параметры его схемы замещения приведем ко вторичной обмотке через коэффициент п = w2/w1, где w2, w1 число витков вторичной и первичной обмоток ТТП.
Все важнейшие характеристики в электрической машине определяются формой тока. Для получения максимального момента она должна соответствовать форме наведенной в ней ЭДС вращения [4]. Для выполнения этого условия в реальной системе и рассматриваемой модели, с учетом допущения для МЭД, полагаем, что электронный преобразователь формирует по сигналам датчика положения ротора фазные напряжения синусоидальной формы с частотой, пропорциональной угловой скорости двигателя: f=pΩ/(2π).Предположим, что внутреннее выходное сопротивление электронного преобразователя равно нулю, а его выходная мощность достаточна, чтобы обеспечить любой режим работы МЭД.
Для расчета характеристик рассмотрим электромагнитные процессы в цепи питания одной фазы (рис. 1), считая другую симметричной, в которой напряжение, токи, ЭДС и потоки смещены по фазе на π/2. При установившейся скорости вращения ротора (Ω = const)для анализа процессов целесообразно применить метод комплексных амплитуд, в соответствии с которым уравнения описываемой системы можно записать так:
U1 = Z1I1 – ZM I2, (–E) = ZM I1 – Z2 I2, I0 = I1 + (-I2) (1)
В этих уравнениях U1, I1, I2, I0E – комплексное изображение входного напряжения, токов в первичной и вторичной обмотках трансформатора и ЭДС вращения в фазе обмотки двигателя.
U1 = U1exp(jθ),
где θ = pθг – начальная фаза входного напряжения относительно начальной фазы ЭДС вращения, θг - геометрический угол между осью катушки датчика положения ротора и осью катушки фазы обмотки магнитоэлектрического двигателя, p–число пар полюсов двигателя; E = E = СeΩ, Сe – постоянная ЭДС вращения, Ω - угловая скорость вращения ротора.
Комплексное сопротивление определяют выражения
Z1 = R1 + jωL1,
Z2 = R2 + Rб + Rд + jωL2,
ZM = jωM.
Для приведённого трансформатора
R1 = R2 = R,
L1 = L2 = L,
M= kL.
Запишем Z1, Z2 и ZM в обобщённых координатах:
Z1 = R(1 + jωτ) = R(1 + jq) =Z1exp (jφ1), Z1 = R(1 + q2)1/2,
φ1 = arctgq,
Z2 = R( 1 + (Rб + Rд)/R + jωτ2) = R(1 + æ + jq) = Z2exp (jφ2),
Z2 = R[(1 + æ)2 + q2]1/2,
φ2 = arctg[q/(1 + æ)],
ZM= jkRq.
Здесь q = ωτ – добротность ТТП, τ = R/L – электромагнитная постоянная времени, æ = (Rб + Rд)/R – коэффициент пропорциональности, R– резистивное сопротивления обмотки ТТП, Rд – сопротивление фазы обмотки двигателя и Rб – сопротивление балластное, шунтирующее фазочувствительных выпрямителей, ω = pΩ - электрическая угловая частота ЭДС вращения и входного напряжения, k – коэффициент магнитной связи.
На рис. 2 представлена векторная диаграмма напряжений и токов приведённого трансформатора, у которого параметры первичной обмотки приведены к вторичной обмотке, в контуре которой происходит преобразование электрической энергии в механическую энергию, через коэффициент трансформации n = w2/w1.
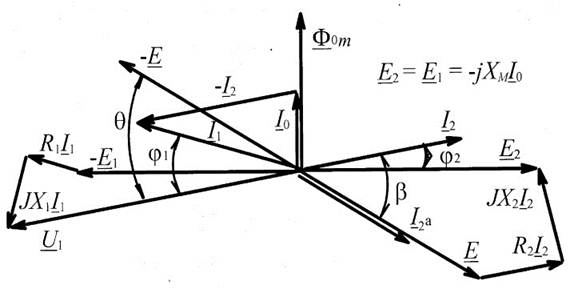
Рис. 2. Векторная диаграмма напряжений и токов.
Диаграмма показывает связи между векторами напряжений и токов.
Решая систему уравнений (1), получим
I1 = (U1Z2 – EZM)/( Z1Z2 – ZM2), I2 = (U1ZM – EZ1)/( Z1Z2 – ZM2). (2)
Полученные решения (2) для токов позволяют определить выражение для электромагнитного момента и КПД двигателя.
Для синусоидальных токов и ЭДС симметричных фаз обмотки сумма мощностей фаз не зависит от времени и поэтому момент постоянен:
М = Pэм/Ω = 2EI2cosβ/ Ω = 2EI2a/ Ω. (3)
Здесь I2a есть составляющая тока I2, совпадающая с вектором (–E) по фазе и, следовательно, участвующая в создании электромагнитного момента. Определим I2a из I2 (2):
I2a = [U1ZMsin(φЭ – q) – EZ1cos(φ1 – φЭ)]/ZЭ2, (4)
где
ZЭ2 = Z1Z2 – ZM2 = ZЭ2exp(jφЭ),
ZЭ2 = r2{[1 + æ – (1 –k2) q2]2 + (2 + æ)2 q2}1/2,
φЭ = arctg[(2 + æ) q/(1 + æ – (1 – k2) q2)],
ZM = kRq.
Подставляя выражение для I2a в (3) и преобразуя его, получим уравнение моментной характеристики М = f(Ω):
М = 2[U1 СeZMsin(φЭ –θ) – Сe2Ω2Z1cos(φ1 – φЭ)]/ZЭ2 (5)
Общепринятая форма представления механической характеристики
Ω = f(М) получается из выражения (5) в виде
Ω = U1СeZMsin(φЭ –θ)/(Сe2Z1cos(φ1 –φЭ)) – МZЭ2/(2Сe2Z1cos(φ1 –φЭ)) (6)
Необходимо заметить, что от угловой скорость вращения ротора Ω зависят значения параметров Z1, Z2, ZM, ZЭ2, φ1, φ2, φЭ, поэтому механическую характеристики целесообразно рассчитывать через моментную характеристику.
Электромагнитный КПД, учитывающий только потери мощности в меди ТТП и МЭД равен
η = Pэм/ P = 2Pэм1/2P1 = EI2a/P1. (7)
Здесь Pэм1, P1 – мощности одной фазы двигателя,
P1 = Re(U1I1*), I1* – комплексно сопряжённое значение тока. С учётом выражений для
U1 = U1exp(jθ), I1 , Pэм1 имеем
η = [U1СeΩZMsin(φЭ–θ) – Сe2Ω2Z1cos(φ1– φЭ)]/[U12Z2cos(φ2 –φЭ) –
-U1СeΩZMsin(φЭ+θ)] (8)
Анализ влияния параметров на вид механической и энергетической характеристик удобно вести в относительных единицах. Так как штатный режим работы системы номинальный, то примем за базовые величины номинальную скорость Ωн, номинальный момент Мн и напряжение питания U1н. Тогда
М = μ Мн, Мн = Pэмн/Ωн, Ω = υΩн,
Pэмн = EнI2a,
α = U1/ U1н.
Переходя к относительным единицам в (5) и в (7), запишем выражения для характеристик μ = f(υ), η = f(υ)
μ = 2 υ [αк1q1sin(φЭ –θ) –
–n(1 + υ2q12)1/2cos(φ1 –φЭ)]/[(1 + æ – (1 – k2) υ2q12)2 + (2 + æ)2 υ2q12]1/2 (9)
η = n[αк1q1sin(φЭ –θ) – n(1 + υ2q12)1/2cos(φ1 –φЭ)]/α[(1 + æ)/υ4 +
+q12/υ2]1/2cos(φ2 –φЭ) – nαkq1sin(φЭ+θ), (10)
Здесь
к1 = Мσ/ Мн, Мσ = U1нСe/R,
n = Eн/U1н, q1 = pτ1Ωн,
φ1 = arctg(υq1),
φ2 = arctg[υq1/(1 + æ)],
φЭ = arctg[(2 + æ)υq1/(1 + æ – (1 – k2)υ2q12)].
Из выражения (9) для моментной характеристики μ = f(υ) видно, что в режиме идеального холостого хода двигателя (μ = 0) υ = υ0 = 0, т.е. МЭД с ТТП не обладает пусковым моментом. На рис. 3 представлены механические и энергетические характеристики для θ= 0 и различных значений U1.
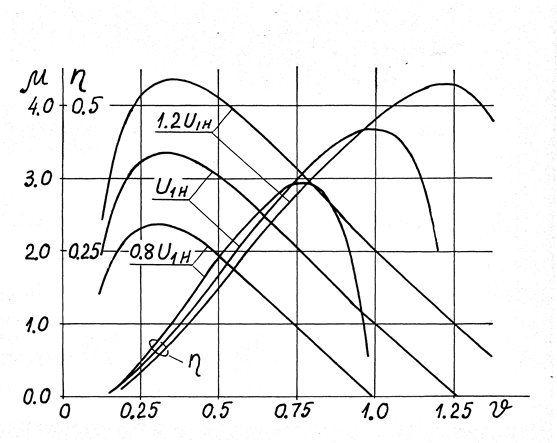
Рис. 3. Механические характеристики и КПД для θ = 0, q = q1 и различных значений U1
Механические характеристики, как видно, в полосе пропускания ТТП для υ> 0.25 аналогичны характеристикам исполнительного двигателя постоянного тока с независимым возбуждением при якорном управлении.
На рис. 4 представлены эти же характеристики для напряжения U1 = U1Н и различных значений его начальной фазы θ, регулируемой методом пространственного смещения обмотки датчика положения ротора.
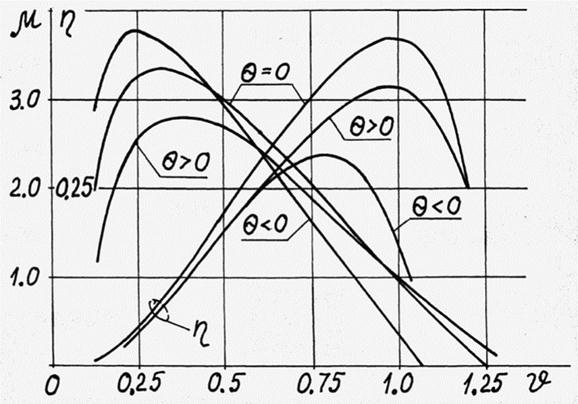
Рис. 4. Механические характеристики и КПД для U1 = U1н, q = q1 и различных значений θ
Изменение фазы входного напряжения приводит к незначительному изменению крутизны механической характеристики, но существенно влияет на η = f(υ). Из анализа характеристик следует, что для получения желаемых характеристик μ = f(υ), η = f(υ) необходимо осуществлять связанное регулирование U1 и θ.
Список литературы
1. Басараб М.А., Кравченко В.Ф., Матвеев В.А. Математическое моделирование физических процессов в гироскопии.- М.: Радиотехника, 2005. - 176 с. - ISBN5-88070-072-0.
2. Рахтеенко Е.Р. Гироскопические системы ориентации. - М.: Машиностроение, 1989. - 223 с.
3. Тарасов В.Н. и др. Сравнительная оценка прецизионных гироскопических электроприводов на базе синхронных электродвигателей // Гироскопия и навигация.- 1996. - № 2 (13). - C. 41-47.
4. Конев Ю.И., Гулякович Г.Н., Полянин К.П. и др. Микроэлектронные системы. Применение в радиоэлектронике / под ред. Ю.И. Конева. - М.: Радио и связь, 1987.- 240 с.
Публикации с ключевыми словами: магнитоэлектрический двигатель, бесконтактный двигатель постоянного тока, диэлектрический статор, бесконтактный трансформаторный токоподвод (ТТП) с ферромагнитными магнитопроводами
Публикации со словами: магнитоэлектрический двигатель, бесконтактный двигатель постоянного тока, диэлектрический статор, бесконтактный трансформаторный токоподвод (ТТП) с ферромагнитными магнитопроводами
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



