научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2012
DOI: 10.7463/1012.0465566
УДК [621.31:63]+631.001.57
Россия, МГТУ им. Н.Э. Баумана
enin@bmstu.ru
Обеспечение качественного управления элементами электроэнергетических систем, в частности синхронными генераторами, при больших возмущениях является необходимым условием их надежного функционирования и живучести. Большие возмущения в сочетании с несовершенством системы противоаварийной автоматики и конструкции генераторов, гидротурбин и другого оборудования могут приводить к авариям с катастрофическими последствиями. Вследствие этого для надежной работы и настройки противоаварийной автоматики требуется анализ динамической устойчивости синхронных генераторов при воздействии различных возмущений. В настоящее время разрабатываются методы анализа динамической устойчивости, основанные на методе функций Ляпунова. Обзору работ по методам анализа динамической устойчивости с использованием функций Ляпунова посвящена работа [1]. В работе основное внимание уделяется методу основанному на сведении многомашинной системе к одномашинному эквиваленту. Однако правомочность такого упрощения, сведения многомашинной системы к одномашинному эквиваленту не достаточно обосновано.
Более обоснованными представляются методы, использующие более полную модель системы: функцию Ляпунова энергетического типа для консервативной модели многомашинной системы [1, 2, 3]. В работах [2, 3] предложена методика анализа запаса динамической устойчивости использующая переходные траектории движения, полученные численным интегрированием и метод функций Ляпунова. Такой подход позволяет расчет переходных траекторий производить с помощью численных методов и достаточно подробных математических моделей системы [4], а для оценки запасов динамической устойчивости упрощенные консервативные модели и метод функций Ляпунова. После расчета траекторий движения производится аппроксимация функции Ляпунова полиномом для заданных возмущений и определяется критическое значение.
1. Математическая модель электроэнергетической системы
Рассмотрим модель системы, которая включает синхронные генераторы, работающие на электрическую сеть. К узлам электрической сети с номерами k = 1, 2, 3, ……, n – подключены синхронные генераторы. Упрощенная модель генератора представляет ЭДС Ek (действующее значение) с фазой θk включенной за реактивным сопротивлением 1/bk. Узлы примыкания генераторов к сети имеют номера k+n, где k – номер узла подключения генератора. К узлам с номерами 2n+1, 2n+2, … , 2n+m подключаются нагрузки. В s-ом узле сети напряжение задается действующим значением Usи фазой θs. К узлу сети может быть подключена комплексная нагрузка Рнs+jQнs. Уравнения для такой системы имеют вид
Tk = Pk -bkEkUk+nsin(θk – θk+n), k
= Pk -bkEkUk+nsin(θk – θk+n), k![]() (1)
(1)
-Pнs + bs-nUsEs-nsin(θs-n – θs)  bskUsUksin(θk – θs) = 0, (2)
bskUsUksin(θk – θs) = 0, (2)
Qнs - bs-nUs2 – UsEs-ncos(θs-n - θs))  bsl(Us2 – UsUlcos(θl – θs) = 0, s
bsl(Us2 – UsUlcos(θl – θs) = 0, s ![]() , (3)
, (3)
где Tk – постоянная времени k-го генератора; Pk – мощность турбины k-го генератора; bsk - реактивная проводимость ветви электрической сети между узлами s и k.
Для исследования взаимных возмущенных движений роторов синхронных генераторов производим в уравнениях (1 – 3) замену переменных δk = θk – θc, k ![]() (где угол θc
(где угол θc ![]() – центр инерции системы) получаем
– центр инерции системы) получаем
Tk¢ = Pk – Tk
= Pk – Tk![]() – bkEkUk+nsin(δk – δk+n), k
– bkEkUk+nsin(δk – δk+n), k![]() (4)
(4)
-Pнs + bs-nEs-nUssin(δs-n – δs) 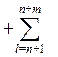 bslUsUlsin(δl – δs) = 0, (5)
bslUsUlsin(δl – δs) = 0, (5)
Qнs – bs-n(Us2 – UsEs-nsin(δs-n – δs)) –![]() (bslUs2 – bslUsUlsin(δl – δs)) = 0, s
(bslUs2 – bslUsUlsin(δl – δs)) = 0, s ![]() (6)
(6)
Нетрудно показать, что для системы (4) – (6) выполняется равенство
![]() (Pk - Tk
(Pk - Tk![]() )
)  Pнs,
Pнs,
и она является консервативной системой, поскольку мощность, вводимая в систему, равна мощности потребляемой нагрузкой.
Функция Ляпунова для консервативной модели системы (4) – (6) имеет вид
V(δ,ω,U) = K(ω) + W(δ,U), (7)
где
K(ω) = K1(w) – K1(ω *), (8)
W(δ,U) = W1(δ,U) – W1(δ *,U*). (9)
V1(δ,ω,U) = K1(ω) + W1(δ,U), (10)
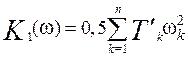 ,
,  , (11)
, (11)
W1(δ,U) = Wa + Wb + Wc, (12)
 ,
,
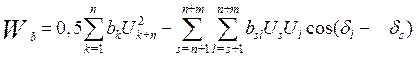 ,
,
 .
.
Δ ![]() . (13)
. (13)
В уравнениях [7 – 10] обозначено: (δ,U) – вектор переменных (δ1, δ2, δ3, …, δn, Un+1, Un+2, …, Un+m, δn+1, δn+2,, …, δn+m ); δ1, δ2, δ3, …, δn– фазы ЭДС генераторов; δn+1, δn+2,, …, δn+m– фазы напряжений в узлах сети относительно угла θс; (δ*,w*,U*) – положение равновесия послеаварийной системы. В консервативной системе Δ = 0.
2. Вычисление критического значения функции Ляпунова и запасов устойчивости
При анализе динамической устойчивости вначале определяется критическое значение функции Ляпунова Wкр. Запас динамической устойчивости вычисляется по формуле
 ,
,
где величина Vвозм вычисляется в момент устранения возмущения (tкз) и равна ![]() . Для поиска критического значения функции Ляпунова на траектории движения определяется точка максимума функции W(δ,U). Точки максимума обозначим Wm. Через точку δ* и точку максимума в многомерном пространстве углов проводится прямая на которой в вычисляются значения функции W(δ,U) [2]. Для более быстрого нахождения критического значения целесообразно использовать полиномиальную аппроксимацию функции W(δ(s),U(s)). В качестве параметра sможно использовать расстояние точек локальных максимумов функции Wот точки положения равновесия (или время отключения возмущения)
. Для поиска критического значения функции Ляпунова на траектории движения определяется точка максимума функции W(δ,U). Точки максимума обозначим Wm. Через точку δ* и точку максимума в многомерном пространстве углов проводится прямая на которой в вычисляются значения функции W(δ,U) [2]. Для более быстрого нахождения критического значения целесообразно использовать полиномиальную аппроксимацию функции W(δ(s),U(s)). В качестве параметра sможно использовать расстояние точек локальных максимумов функции Wот точки положения равновесия (или время отключения возмущения)
 .
.
Пусть заданы значения параметра tdи соответствующие им значения функции W на прямой в многомерном пространстве
s0, s1, s2, s3, ….., sK+1,
W(s0), W(s1), W(s2), W(s3), …, W(sK+1).
Представим интерполяционный полином, проходящий через K+1 точку функции f(s), в виде
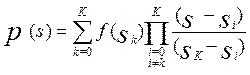 . (14)
. (14)
Аппроксимируем функцию W(δ(s)) локальных максимумов заданную в K+2 точках полиномом вида (14). Тогда для наилучшей аппроксимации должно выполняться
 .
.
Погрешность аппроксимации в заданных точках будет равна
 .
.
Полином, аппроксимирующий функцию W(s), тогда будет иметь вид
 . (15)
. (15)
Критическое значение функции Ляпунова определим из условия
 .
.
Дифференцируя выражение (15) по sи учитывая, что
 ,
,
получаем уравнение для определения sкр при котором функция Wm(s) принимает максимальное значение:
 , (16)
, (16)
где ![]() .
.
Для повышения точности при определении критического значения следует выбирать полином более высокой степени.
В качестве примера рассматривалась трехмашинная электроэнергетическая система, в которой три генератора через линию электропередачи работают на общую нагрузку. Аварийный процесс вызывается трехфазным КЗ на линии 2. Возмущение вызывает переходный процесс, который может привести к нарушению синхронной работы генераторов. Возмущение деблокируется отключением КЗ и одной цепи линии. По результатам расчетов при различных длительностях КЗ были получены следующие значения максимумов функции W(td) на траектории
s0 = 0.0, s1 = 0.365, s2 = 0.945, s3 = 0.9625, s4 = 0.979, s5 = 1.095;
Wm(s0) = 0, Wm(s1) = 0.0115, Wm(s2) = 0.04, Wm(s3) = 0.0491, Wm(s4) = 0.0495, Wm(s5) = 0.029.
С использованием выражений (15), (16) (использовался полинома четвертой степени) было вычислено критическое значение функции Ляпунова равное Wкрит = 0.0548 и критическое время деблокирования tкрит=0.1648. Результаты расчета запаса динамической устойчивости по этим данным приведены в таблице.
Таблица. Запасы устойчивости при различных длительностях КЗ
tКЗ, с | Vвозм | Wкр | Kд, % |
0,05 | 0,0040 | 0,0548 | 92 |
0,10 | 0,0115 | -» | 79 |
0,15 | 0,0400 | -» | 27 |
0,16 | 0,0495 | -» | 9 |
0,17 | 0,0605 | -» | -10 |
В таблице обозначено: tКЗ – длительность короткого трехфазного замыкания; Vвозм – значение функции Ляпунова после деблокирования возмущения; Wкрит – критическое значение функции Ляпунова; KД – коэффициент запаса устойчивости (в процентах).
Особо опасными режимами для мощных синхронных гидрогенераторов считаются короткие трехфазные замыкания на шинах, которые могут приводить к выделению большой мощности и разрушению гидроагрегата. Далее рассматривается динамическая устойчивость одного из мощных синхронных генераторов 6400 МВт работающих параллельно на линию передач 525 кВ. Динамическая устойчивость исследовалась при воздействии возмущения в виде КЗ на шинах генератора. Исследование проводилось с использованием системы моделирования динамических систем MATLAB. Запасы устойчивости и критическое время отключения возмущения определялось с использованием предлагаемой методики. Параметры синхронного генератора СВФ 1285/275–42 УХЛ4:
Sн = 711 МВА; Uн =15.75 кВ; nн = 142.8 об/мин; J = 25400 тм
xs=0.184; xd= 1.58; xd' = 0.43; xd'' = 0.295; xq= 0.97; xq' = 0.31; (о. е.)
Td0 = 8.21 с; Td0' = 0.143 с.
Параметры трансформатора:
Sн = 711 МВА; Uнн =15.75 кВ; Uвн =525 кВ;
ΔPx= 500 кВт; Ix= 0.35 %; ΔPк = 1300 кВт; uк =14 %.
Структурная схема в Simulinkс использованием блоков расширения SimPoweSystems приведена на рис. 1.

Рис 1. Структурная схема в системе MATLABмощного синхронного генератора работающего на линию 525 кВ
Проводилось моделирование системы (рис. 2) при различных длительностях КЗ на шинах синхронного генератора. Результаты моделирования: напряжение на шинах генератора (фаза C); фаза ЭДС генератора для случая нарушения динамической устойчивости приведены на рис. 2 – 3.

Рис. 2. Напряжение статора фазы C (КЗ на шинах генератора, о. е.).

Рис. 3. Изменение фазы ЭДС генератора относительно синхронной оси при КЗ на шинах генератора (потеря устойчивости), о. е.
При различных длительностях КЗ на шинах проводился расчет переходных процессов и анализ динамической устойчивости синхронного генератора. Анализ проводился с использованием функций Ляпунова энергетического типа. Проведенные расчеты были использованы для аппроксимации функции Wmв зависимости от длительности КЗ. Затем было найдено критическое время отключения возмущения (tкрит≈0.105 с).
Предлагаемая и развиваемая методика анализа динамической устойчивости синхронных генераторов совмещает преимущества методов численного моделирования и качественных методов (методов функций Ляпунова). Применение этой методики предполагает вычисление функции Ляпунова для всех точек многомерной траектории переходного процесса, получаемой численным интегрированием уравнений динамики системы. Это позволяет получать не только траектории движения при воздействии возмущения, но и производить некоторую интегральную оценку динамической устойчивости, для более эффективной настройки системы протиаварийного автоматического управления синхронными генераторами.
Список литературы
1. Павелла М. От общей теории Ляпунова к практическому прямому методу анализа динамической устойчивости энергосистем // Электричество. 2000. № 6. C. 14-26.
2. Авраменко В.Н., Степанов А.В. Определение запаса динамической устойчивости энергосистем прямым методом Ляпунова // Техническая электродинамика. 1999. № 5. C. 55-58.
3. Кузовкин В.А., Степанов А.В. Оценка запаса динамической устойчивости энергосистем прямым методом Ляпунова // Электричество. 2002. № 1. C. 2-8.
4. Строев В.А., Шульженко С.В. Математическое моделирование элементов электрических систем : курс лекций. М.: Издательство МЭИ, 2002. 56 с.
Публикации с ключевыми словами: переходные процессы, синхронный генератор, электроэнергетические системы, динамическая устойчивость, функция Ляпунова
Публикации со словами: переходные процессы, синхронный генератор, электроэнергетические системы, динамическая устойчивость, функция Ляпунова
Смотри также:
- Развитие прямого метода Ляпунова для анализа динамической устойчивости системы синхронных генераторов на основе определения неустойчивых положений равновесия на многомерной сфере
- Обзор литературных источников по моделированию динамики процесса сверления
- 77-48211/478777 Использование электрического моделирования для анализа состояния магнитной цепи электрических машин с постоянными магнитами. (ч.1).
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



