научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#8 август 2004
Э.Д. Аведьян, д-р техн. наук,
Институт проблем управления РАН
Ассоциативная нейронная сеть СМАС.
Структура, объем памяти, обучение и базисные функции
Приводится описание нейронной сети и алгоритм нелинейного преобразования аргументов. Определяется объем памяти сети и дается ее алгоритм обучения. Устанавливаются свойства базисных функций сети.
1. ВВЕДЕНИЕ
СМАС — сокращенное название нейронной сети, которое происходит от первых букв ее полного английского названия: Сегеbellar Model Articulation Controller (мозжечковая модель суставного регулятора). Эта нейронная сеть, в основу которой положена нейрофизиологическая модель мозжечка, была разработана американским ученым Альбусом [1], [2]. Первоначально нейронная сеть СМАС была предназначена для управления роботом-манипулятором. В последующих работах Толле и его соавторов (в частности, в работах [3], [4]) было показано, что эта нейронная сеть может быть успешно применена для идентификации и управления нелинейными динамическими объектами. Подчеркивая новую область применения нейронной сети, авторы назвали ее AMS (Associative Memory System). Это название более точно отражает природу нейронной сети СМАС, поскольку она может выступать не только в роли регулятора системы управления или робота- манипулятора, но и в роли модели сложной нелинейной динамической системы. Тем не менее, первоначальное английское название СМАС прочно закрепилось за этой нейронной сетью.
Исследования, касающиеся различных аспектов СМАС, отражены в монографиях [5], [6] и во многих журнальных статьях. Характерным для нейронной сети СМАС является ее успешное применение в реальных и модельных системах управления динамическими процессами [4], [5], [7]-[11] и в системах управления роботами-манипуляторами [1], [12]. Сеть здесь обычно выступает в роли регулятора системы управления. В ней хранится информация, позволяющая определить управляющее воздействие как функцию вектора состояния и вектора управления нелинейной динамической системы.
СМАС предназначена для запоминания, восстановления и интерполяции функций многих переменных. Как и в любой нейронной сети, в СМАС существуют два основных принципиально различных процесса:
• процесс обучения, который осуществляется по измерениям значений функции и ее векторного аргумента с помощью соответствующего алгоритма;
• процесс восстановления, когда по входному вектору восстанавливается или оценивается значение этой функции.
Алгоритм обучения этой нейронной сети предложил ее автор в работе [2] без доказательства, основываясь в основном на экспериментальных результатах и на понимании того факта, что после очередного шага обучения нейронная сеть способна точно восстановить значение функции при значении аргумента, при котором произошло обучение. Доказательство сходимости алгоритма обучения и исследование его некоторых свойств было дано в работе Милитцера и Паркса [13] которые показали, что алгоритм обучения СМАС эквивалентен итеративному процессу решения системы линейных алгебраических уравнений. В роли неизвестных этой системы уравнений выступают настраиваемые веса нейронной сети, а в роли матрицы системы уравнений — матрица, сформированная из ассоциативных векторов, о которых речь будет идти ниже. В этой работе особо были рассмотрены случаи, когда система уравнений совместна и когда она несовместна. В последнем случае авторы выделили зону, в которую сходятся и в которой изменяются оценки весовых коэффициентов после завершения процесса обучения. Эта зона была названа авторами зоной притяжения. В работе Аведьяна и Хормеля [14] было отмечено (см. также [15]), что алгоритм обучения в форме Милитцера и Паркса [13] представляет собой классический алгоритм решения системы линейных алгебраических уравнений, описанный Качмажем [16] в 1937 г., и на этой основе был предложен ускоренный алгоритм обучения СМАС. Описание и исследование алгоритма Качмажа можно найти во многих работах, например [14], [15], [17]—[26]. Этот алгоритм неоднократно предлагался вновь различными авторами, и в литературе по автоматическому управлению он часто фигурирует под другими названиями, например, в работе [27] этот алгоритм называется либо α — LMS (α — Least Mean Square) алгоритмом, либо дельта - правилом Уидроу—Хоффа, в работе [6] авторы называют его NLMS (Normalised Least Mean Square) — training rule. Интерполяционные возможности обученной нейронной сети СМАС частично исследованы в работах [28], [29], в которых показано, что она, в отличие от многослойных нейронных сетей, не способна точно восстанавливать все функции.
2. СТРУКТУРА НЕЙРОННОЙ СЕТИ СМАС
Следующие два отличительных момента характеризуют эту нейронную сеть, которая, как отмечалось выше, предназначена для запоминания и восстановления функций многих переменных:
• значения аргументов функции принимают только дискретные значения;
• нелинейное преобразование аргументов функции осуществляется неявно с помощью алгоритма вычисления адресов ячеек ассоциативной памяти, в которых хранятся числа, определяющие значение функции.
2.1. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ В СМАС
Чтобы запомнить функцию многих переменных с помощью нейронной сети СМАС, сначала задается область определения этой функции на гиперпараллелепипеде, вершинами которого являются минимальные и максимальные значения аргументов этой функции; далее ребра гиперпараллелепипеда квантуются с постоянным шагом по каждому ребру, и дискретизованным значениям аргументов присваиваются целочисленные номера. Эти номера однозначно связаны со значениями аргументов функции. Так, для функции одной переменной у(х) аргумент х1 связан со своим номером i следующим соотношением
xi = xmin + (i - 1) ∆x (1)
где 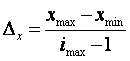 — шаг
квантования; xmin, xmax
— минимальное и максимальное значения аргумента х из области определения; i
=
1, imax где imax
число точек, на которых задана функция у(х). Номер i
можно рассматривать как относительный аргумент функции, поскольку соотношение
(1) описывает процедуру сдвига и масштабирования исходной области определения
функции. Поэтому в дальнейшем будем считать, что значения аргументов
запоминаемой в СМАС функции принимают только целочисленные значения, т.е.
функция у(х) от N переменных х = (х1,
х2 ..., хN)Т
определена на целочисленной N-мерной сетке у(х):
— шаг
квантования; xmin, xmax
— минимальное и максимальное значения аргумента х из области определения; i
=
1, imax где imax
число точек, на которых задана функция у(х). Номер i
можно рассматривать как относительный аргумент функции, поскольку соотношение
(1) описывает процедуру сдвига и масштабирования исходной области определения
функции. Поэтому в дальнейшем будем считать, что значения аргументов
запоминаемой в СМАС функции принимают только целочисленные значения, т.е.
функция у(х) от N переменных х = (х1,
х2 ..., хN)Т
определена на целочисленной N-мерной сетке у(х):
![]()
2,2. АЛГОРИТМ НЕЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ АРГУМЕНТОВ, ИЛИ АЛГОРИТМ ВЫЧИСЛЕНИЯ АДРЕСОВ АССОЦИАТИВНОЙ ПАМЯТИ
При построении алгоритма вычисления адресов ассоциативной памяти и алгоритма обучения СМАС ее автор [1] исходил из нейрофизиологического подхода.
Согласно этому подходу каждый входной сигнал возбуждает определенную область мозжечка, суммарная энергия которой соответствует значению запоминаемой функции. В нейронной сети СМАС предполагается, что каждый входной сигнал (аргумент функции) возбуждает, или делает активными, ровно p* ячеек памяти, суммарное содержание которых равно значению запоминаемой функции. Следовательно, даже в случае скалярного аргумента х = х1 ему соответствует мерный вектор номеров активных ячеек памяти. Параметр p* играет очень важную роль. В литературе он известен как обобщающий параметр (generalization parameter) его значение определяет разрешающую способность СМАС и требуемый объем памяти.
Одномерный случай
Каждому значению скалярного аргумента ![]() соответствует ровно p* активных ячеек памяти с номерами
соответствует ровно p* активных ячеек памяти с номерами
![]() (З)
(З)
так что
максимальному значению аргумента ![]() соответствуют ячейки памяти с
номерами
соответствуют ячейки памяти с
номерами ![]() ,
откуда следует, что число ячеек памяти, необходимых для хранения функции одной
переменной в СМАС, равно
,
откуда следует, что число ячеек памяти, необходимых для хранения функции одной
переменной в СМАС, равно
![]() (4)
(4)
что на p* - 1 больше числа значений функции, запоминаемых нейронной сетью. Таким образом, в одномерном случае нейронная сеть СМАС, с точки зрения требуемого объема памяти, неэффективна, однако ее эффективность проявляется при достаточно точном запоминании гладких функций по небольшому числу обучающей последовательности n<<M(1).
Очевидно, что
номера активных ячеек памяти, соответствующие скалярной переменной ![]() можно
представить p* -мерным вектором m(1),
значения компонент которого равны номерам активных ячеек. Из последующего
изложения следует, что последовательность значений компонент
можно
представить p* -мерным вектором m(1),
значения компонент которого равны номерам активных ячеек. Из последующего
изложения следует, что последовательность значений компонент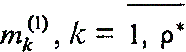 , вектора m(1)
, вектора m(1)
в одномерном случае не существенна. В многомерном случае она, однако, приобретает принципиальное значение.
Далее приводится алгоритм формирования вектора номеров активных ячеек для одномерного случая, поскольку он служит основой построения вектора - номеров активных ячеек в многомерном случае. Этот алгоритм обеспечивает (в соответствии с приведенным в работе [1] требованием) однозначное соответствие номера компоненты k вектора m(1) и ее значения mk(1).
Таблица
Введем функцию
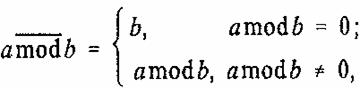 (5)
(5)
где a mod b — остаток от деления a на b, где a и b — целые числа.
Тогда
значения всех p* компонент ![]() вектора m(1) вычисляются согласно выражению
вектора m(1) вычисляются согласно выражению
![]() (6)
(6)
т.е. чем меньше расстояние между двумя значениями аргумента, тем больше общее число ячеек памяти, соответствующих этим значениям аргумента.
для
вычисления компонент вектора m(1) согласно
выражению (6) достаточно определить номер ![]() -той компоненты, значение которой равно
х1 т.е. вычислить (6) при i=0.
Значения следующих компонент равны х1 + 1, х2
+ 2 и т.д., при этом полагается, что номера компонент замкнуты в кольцо, т.е.
после компоненты с номером p* следует компонента с
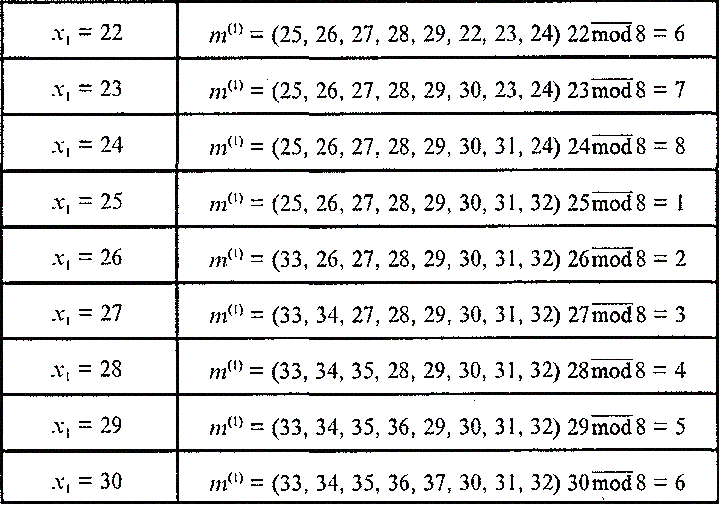
номером 1. В качестве поясняющего примера в таблице приведены выражения для
вектора m(1) размерности p*
= 8 для ряда значений аргумента х1 = 22, 23, 24, 25, 26, 27,
28, 29, 30.
-той компоненты, значение которой равно
х1 т.е. вычислить (6) при i=0.
Значения следующих компонент равны х1 + 1, х2
+ 2 и т.д., при этом полагается, что номера компонент замкнуты в кольцо, т.е.
после компоненты с номером p* следует компонента с
номером 1. В качестве поясняющего примера в таблице приведены выражения для
вектора m(1) размерности p*
= 8 для ряда значений аргумента х1 = 22, 23, 24, 25, 26, 27,
28, 29, 30.
Из таблицы следует, что если двум различным значениям аргумента х1 соответствуют одинаковые номера активных ячеек, то эти номера всегда являются одними и теми же компонентами вектора m(1) при этом первой компонентой вектора m(1) оказываются такие номера ячеек, остаток от деления которых на p* равен единице; второй компонентой вектора m(1) оказываются такие номера ячеек, остаток от деления которых на p* равен двум, и т.д.
Из последовательностей (3) и соотношения (б) следует, что если для двух значений аргумента х равных х = с и х = а’, выполняется условие
![]() (7)
(7)
то число общих ячеек памяти j, соответствующее этим значениям аргумента, равно
∆p = p*-p,
т.е. чем меньше расстояние между двумя значениями аргумента, тем больше общее число ячеек памяти, соответствующих этим значениям аргумента.
Многомерный случай
В многомерном
случае, когда нейронная сеть СМАС запоминает функцию у(х)N
переменных x=(x1, x2,…,xN)T, заданных на целочисленной сетке ![]() , входному N-мерному вектору х также ставится в соответствие p*-мерный вектор m активных ячеек
памяти. Вычисление номеров активных ячеек памяти выполняется с помощью
описываемого далее алгоритма.
, входному N-мерному вектору х также ставится в соответствие p*-мерный вектор m активных ячеек
памяти. Вычисление номеров активных ячеек памяти выполняется с помощью
описываемого далее алгоритма.
Каждой компоненте x, ![]() вектора х соответствует
p*-мерный вектор m(1)
активных ячеек памяти. Значения всех p* вектора m(1) — вычисляются, как это было описано выше
в
одномерном случае, согласно выражению (6). В результате этих вычислений вектору
х ставится в соответствие промежуточная матрица М активных ячеек памяти с
элементами
вектора х соответствует
p*-мерный вектор m(1)
активных ячеек памяти. Значения всех p* вектора m(1) — вычисляются, как это было описано выше
в
одномерном случае, согласно выражению (6). В результате этих вычислений вектору
х ставится в соответствие промежуточная матрица М активных ячеек памяти с
элементами
![]()
 (8)
(8)
На следующем шаге матрице М размера N x p* ставится в соответствие p*-мерный вектор активных ячеек памяти вектора х. Для этого выполняется последовательное слияние (concatenation) элементов каждого k-го столбца матрицы М в один k-й элемент вектора активных ячеек памяти m, так что этот вектор приобретает следующий вид:
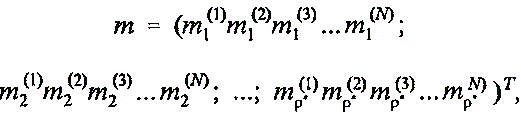
каждый элемент которого
![]() (9)
(9)
однозначно
определяет номер активной ячейки памяти СМАС. Выражение (9) можно трактовать
как позиционную запись числа mk старший
разряд которого, равен ![]() младший разряд —
младший разряд — ![]() . К
особенностям чисел, образующих символьную запись числа mk(9),
относится отмеченный выше факт, заключающийся в том, что остаток от деления
каждого из них на p* равен k.
Алгоритм вычисления числа mk, по значениям
. К
особенностям чисел, образующих символьную запись числа mk(9),
относится отмеченный выше факт, заключающийся в том, что остаток от деления
каждого из них на p* равен k.
Алгоритм вычисления числа mk, по значениям ![]() принимает
наиболее простую форму, когда максимально возможные значения компонент вектора
х удовлетворяют следующему соотношению:
принимает
наиболее простую форму, когда максимально возможные значения компонент вектора
х удовлетворяют следующему соотношению:
![]() (10)
(10)
Согласно (4) число ячеек памяти, необходимых для хранения функций одной переменной в СМАС, оказывается равным
![]() (11)
(11)
В этом случае алгоритмы вычисления mk который приводится без доказательства, имеет вид
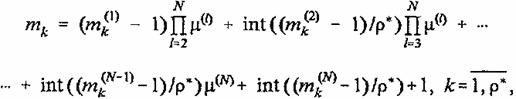 (12)
(12)
где int (a / b) — функция целочисленного деления a на b.
Пример
В качестве иллюстративного примера рассмотрим сеть со следующими
параметрами: размерность N входного вектора равна 2,
параметр![]() , так
что согласно (10)
, так
что согласно (10) ![]() , и, следовательно,
, и, следовательно, ![]() (2).
(2).
Найдем номера ячеек памяти СМАС согласно выражениям (6), (8), (9) и (12), которые соответствуют входному вектору x[1]=(6;8)

Пересчитывая символические номера 9, 9; 6, 10; 7, 11; 8,8 активных ячеек в соответствии с алгоритмом (12), получим
9,9→8*3+2+1=27
6,10→5*3+2+1=18
7,11→6*3+2+1=21
8,8→7*3+1+1=23,
так что вектор номеров активных ячеек. соответствующий вектору x[1]=(6; 8)T, равен
m[1]=(27, 18, 21, 23)T
Не приводя промежуточных результатов, заметим, что вектор x[2]=(7, 6)T соответствует
вектору номеров активных ячеек в символическом m[2] =
(9, 9; 10, 6; 7, 7; 8, 8)T и в десятичном m[2]= (27, 29, 20, 23)T
представлениях, и, следовательно, ячейки памяти с номерами 23 и 27 активируются
как вектором x[1] так и вектором .x[2].
Отметим здесь, что общее число ячеек памяти для рассматриваемой сети М = 36,
тогда как возможное число точек запоминаемой функции равно ![]() .
.
2.3. ОБЪЕМ ПАМЯТИ
Необходимое число ячеек памяти М нейронной сети СМАС следует из формулы
(12), когда все числа ![]() принимают свои максимально
возможные значения, т.е. когда
принимают свои максимально
возможные значения, т.е. когда ![]() . При этом сомножители
. При этом сомножители ![]() , входящие в
формулу (12), оказываются равными
, входящие в
формулу (12), оказываются равными
![]() (13)
(13)
а величина М задается выражением
 (14)
(14)
Соотношения
(10) и (14) позволяют выразить объем памяти СМАС в функции ![]() где
где ![]() — наибольшее значение,
которое принимает аргумент xl:
— наибольшее значение,
которое принимает аргумент xl:
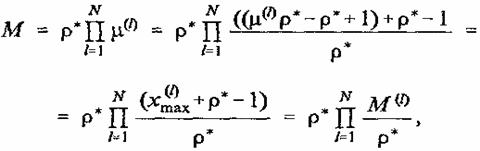 ` (15)
` (15)
где M(l) определено соотношением (11).
Если бы функция многих переменных у(х) хранилась в памяти обычным способом, когда значение функции записывается в одну ячейку памяти, то для этого, очевидно, понадобилось бы
 (16)
(16)
ячеек памяти, что следует также из формулы (15) при p* = 1, когда в СМАС каждый входной сигнал возбуждает только одну ячейку памяти. Из сравнения выражений (15) и (16) следует, что СМАС уменьшает объем памяти по сравнению с обычным способом хранения приблизительно в (p*)N-1 раз, так что эффективность его с точки зрения требуемого объема памяти растет с увеличением размерности входного вектора.
Пользуясь выражением (15), можно исследовать влияние параметра p* на объем памяти СМАС при фиксированных
характеристиках входного вектора х. Наиболее удобно сделать это, когда функция
у(х) задана на гиперкубе, т.е. когда все значения ![]() , одинаковы и равны
, одинаковы и равны
![]() (17)
(17)
Полагая
![]() (18)
(18)
найдем μo = μ(l)(10) и Mo=M(l)(11):
![]() (19)
(19)
Объем памяти СМАС согласно (15) в этом случае равен
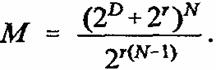 (20)
(20)
Нетрудно показать, что объем памяти М (20) с ростом параметра p* убывает и достигает минимально возможного значения при p*(r)=2D
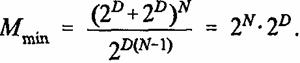 (21)
(21)
Таким образом, коэффициент выигрыша объема памяти т определяемый как отношение объема памяти М
(16) при обычном способе хранения информации к объему памяти СМАС Мmin, принимает наибольшее значение при p*(r)=2D и оказывается равным
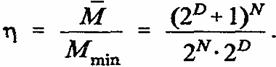
При D ≥ 5 выражение для коэффициента η с большой точностью можно принять равным η=2DN-D-N. В частности, если хранить изображение, заданное на двумерной сетке (210+1)*(210+1) обычным способом, то понадобится один мегабайт памяти, тогда как если это изображение запомнить в СМАС при максимально возможном значении коэффициента p*(r)=210, то можно ограничиться только четырьмя килобайтами памяти.
2.4. ВЫХОД НЕЙРОННОЙ СЕТИ СМАС
Как отмечалось в начале п. 2.2, значение запомнен ной в СМАС функции y(х) равно сумме содержимого активных ячеек памяти. для формализации понятия “выход сети” введем следующие переменные:
w[n] — М - мерный вектор памяти сети, вычисленный на п-м шаге обучения, каждая]-я компонента которого
![]() соответствует
содержимому ‚-й ячейки памяти СМАС;
соответствует
содержимому ‚-й ячейки памяти СМАС;
а(х) — М
-
мерный ассоциативный вектор, однозначно связанный с вектором аргументов х
посредством вектора т (9) номеров активных ячеек памяти по следующему правилу:
элементы вектора а ![]() , номера которых совпадают
с номерами активных ячеек памяти, равны единице, все остальные элементы вектора
а равны нулю. Следовательно, в векторе а всегда p*
элементов равны единице. Тогда в соответствии с правилом функционирования
нейронной сети СМАС ее выход ŷ(x,n) при заданном входном векторе х равен
, номера которых совпадают
с номерами активных ячеек памяти, равны единице, все остальные элементы вектора
а равны нулю. Следовательно, в векторе а всегда p*
элементов равны единице. Тогда в соответствии с правилом функционирования
нейронной сети СМАС ее выход ŷ(x,n) при заданном входном векторе х равен
![]() (22)
(22)
т.е. выход равен сумме содержимого активных ячеек памяти сети. Такое представление выхода сети было введено в работе Милитцера и Паркса [13] оно позволило понять природу этой нейронной сети, исследовать процесс обучения в ней и найти пути повышения ее эффективности.
3. ОБУЧЕНИЕ В НЕЙРОННОЙ СЕТИ СМАС
Процесс формирования М - мерного вектора памяти w,
направленный на запоминание функции y(x)N переменных x=(x1,
x2,…,xN)T заданных на целочисленной сетке ![]() называется обучением.
Алгоритм обучения нейронной сети СМАС был предложен Альбусом в работе [1].
Этот алгоритм, имеющий рекуррентную природу, функционирует следующим образом.
называется обучением.
Алгоритм обучения нейронной сети СМАС был предложен Альбусом в работе [1].
Этот алгоритм, имеющий рекуррентную природу, функционирует следующим образом.
Пусть после (n - 1)-го измерения значений
запоминаемой функции у(х) и соответствующих значений вектора аргументов ![]() был вычислен
вектор памяти w[n-1]. Тогда на
следующем n - м шаге, после измерения значения функции
у[n], при известном значении аргумента х[n] сначала с помощью “алгоритма нелинейного преобразования”
аргументов (см. п. 2.2) вычисляются номера активных ячеек памяти, т.е.
вычисляется соответствующий вектору х[n] вектор m[k] (9), (12), далее вычисляется
предсказываемое нейронной сетью в соответствии с предыдущим п. 2.4 значение
функции ŷ[k] равное сумме
содержимого активных ячеек памяти. Вычисляются ошибка предсказания
был вычислен
вектор памяти w[n-1]. Тогда на
следующем n - м шаге, после измерения значения функции
у[n], при известном значении аргумента х[n] сначала с помощью “алгоритма нелинейного преобразования”
аргументов (см. п. 2.2) вычисляются номера активных ячеек памяти, т.е.
вычисляется соответствующий вектору х[n] вектор m[k] (9), (12), далее вычисляется
предсказываемое нейронной сетью в соответствии с предыдущим п. 2.4 значение
функции ŷ[k] равное сумме
содержимого активных ячеек памяти. Вычисляются ошибка предсказания ![]() и величина
коррекции
и величина
коррекции ![]() которая
прибавляется к содержимому активных ячеек памяти. Неактивные ячейки коррекции
не подвергаются.
которая
прибавляется к содержимому активных ячеек памяти. Неактивные ячейки коррекции
не подвергаются.
Если воспользоваться введенным вп. 2.4 ассоциативным вектором а,
однозначно связанным с вектором m (9) номеров
активных ячеек памяти по следующему правилу: элементы вектора ![]() , номера
которых совпадают с номерами активных ячеек памяти, равны единице, все
остальные элементы вектора а равны нулю, то алгоритм обучения СМАС можно
записать в следую щей форме:
, номера
которых совпадают с номерами активных ячеек памяти, равны единице, все
остальные элементы вектора а равны нулю, то алгоритм обучения СМАС можно
записать в следую щей форме:
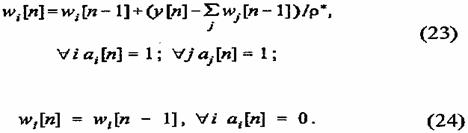
Последовательность w[n] (23), (24) устроена так, что после коррекции вектора памяти w[n-1] -оценка функции y[n] которая является суммой содержимого активных ячеек, совпадает с ее значением, т.е.
![]() (25)
(25)
Это утверждение следует непосредственно из суммирования правой и левой частей уравнения (23) по активным номерам ячеек памяти.
Альбус исследовал сходимость алгоритма только экспериментально. Теоретическое обоснование сходимости последовательности (23), (24) впервые было дано в работе Милитцера и Паркса [13] [30] которые показали, что алгоритм обучения СМАС есть итеративный процесс решения системы линейных уравнений относительно неизвестных значений компонент вектора памяти w. Вопросы сходимости процедуры (23), (24) обсуждались также в работе [31]. В работе [13] было показано, что в зависимости от вида запоминаемой функции и параметров СМАС последовательность w[n] (23), (24) сходится либо в точку, либо в некоторую область, которую авторы назвали зоной притяжения. Основой доказательства сходимости последовательности w[n] послужило представление алгоритма (23), (24) в эквивалентной векторной форме:
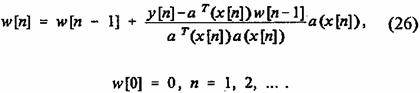
В работе [14] было отмечено, что предложенный Альбусом алгоритм обучения в форме (26) является известным алгоритмом Качмажа [16], [17] для итеративного решения системы линейных уравнений вида
![]()
и поэтому в дальнейшем алгоритм (23), (24) обучения нейронной сети СМАС будем называть алгоритмом Альбуса — Качмажа. Представление алгоритма обучения в форме (26) позволило в работе [14] предложить и исследовать алгоритм обучения, обладающий повышенной скоростью сходимости, который будет описан во второй части статьи. С помощью такого представления также удалось повысить точность восстановления запоминаемых функций [32].
Система уравнений (27) обладает рядом особенностей:
• в каждом уравнении системы ровно p* коэффициентов равны единице, все остальные коэффициенты равны нулю;
• как правило, размерность М вектора и’ существенно больше числа ненулевых элементов вектора, число которых равно p* так что матрица системы (27) является сильно разреженной матрицей;
• поскольку максимально возможное число линейно независимых уравнений системы (27) равно числу неизвестных, равному размерности М вектора w а максимальное число уравнений равно числу точек
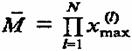 целочисленной сетки
целочисленной сетки
![]()
и, как
правило, ![]() (напомним, что
(напомним, что 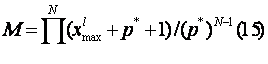 ), то эта
система уравнений обычно несовместна;
), то эта
система уравнений обычно несовместна;
• система уравнений (27) всегда имеет единственное решение в случае, когда параметр p* = 1; при этом матрица системы равна единичной матрице или легко преобразуется к ней путем перенумерования последовательности y. Этот случай соответствует обычному способу хранения информации, когда в каждой ячейке памяти хранится значение функции, а номер ячейки памяти однозначно связан с аргументом функции.
Несовместность системы уравнений (27) приводит к тому, что последовательность y[n] (26) сходится в зону решения (“зону притяжения” [13]) и совершает там движения в соответствии с алгоритмом обучения сети (26) и законом формирования входного вектора x[n]. За решение принимается одно из значений вектора w[n] которое принадлежит зоне притяжения.
4. “МАШИННАЯ РЕАЛИЗАЦИЯ” ВЫХОДА НЕЙРОННОЙ СЕТИ СМАС
Уравнение (22), будучи простой и удобной вычислительной процедурой нахождения выхода сети, скрывает, однако, систему функций, по которой происходит разложение аппроксимируемой функции. Для нахождения этой системы функций воспользуемся представлением алгоритма обучения в виде функционального уравнения так, как это сделано в работе Цыпкина [33]. С этой целью умножим обе части уравнения (26) на вектор aT(x) и получим следующее рекуррентное функциональное уравнение:
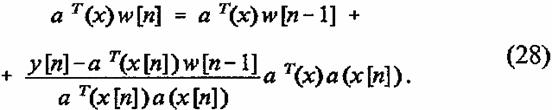
Из выражения (22), определяющего выход сети при заданном входном
векторе x[n] и
фиксированном векторе памяти![]() , следует, что выражения
, следует, что выражения ![]() =aT(x)w[n] и
=aT(x)w[n] и ![]() , входящие в
правую и левую части уравнения (28), определяют функции, которые аппроксимирует
ее выход на n-м и на (а - 1)-м шагах обучения.
Поскольку выражение
, входящие в
правую и левую части уравнения (28), определяют функции, которые аппроксимирует
ее выход на n-м и на (а - 1)-м шагах обучения.
Поскольку выражение
![]() определяет
выход сети после (n - 1)-го шага обучения при входном
векторе x[n] и aT(x[x])a(x[n])=p*, уравнение (28) можно переписать в следующей
эквивалентной форме:
определяет
выход сети после (n - 1)-го шага обучения при входном
векторе x[n] и aT(x[x])a(x[n])=p*, уравнение (28) можно переписать в следующей
эквивалентной форме:
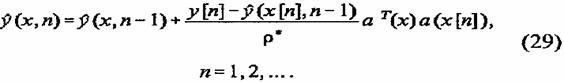
Обозначим
коэффициент ![]() и функцию
и функцию
![]() (30)
(30)
Тогда решение уравнения (29) принимает вид:
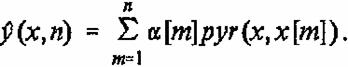 (31)
(31)
При решении уравнения (29) предполагалось, что до начала процесса обучения вектор памяти сети w[0] равен нулю. В противном случае решение уравнения (29) равно
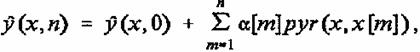 (32)
(32)
где р (х, О) — функция, которая соответствует ненулевому значению вектора памяти ч’ О до начала процесса обучения.
Представление выхода сети выражениями (31) и (32) соответствует “машинной реализации” аппроксимационной процедуры метода потенциальных функций [34], тогда как представление выхода выражением (22) соответствует “персептронной реализации” этого метода. Машинная реализация позволяет выяснить многие свойства нейронной сети СМАС, в то время как персептронная реализация является основной вычислительной схемой построения аппроксимационной функции.
4.1. БАЗИСНЫЕ ФУНКЦИИ НЕЙРОННЫХ СЕТЕЙ
Под базисными функциями нейронных сетей обычно понимаются функции,
линейная комбинация которых аппроксимирует функцию, которую запоминает
нейронная сеть [6]. Такими функциями, например, для нейронной сети RBF (Радиальные Базисные Функции) [6], [25], [35]-[37]
являются функции, структура которых имеет вид y(x)=f(r),
где ![]() ,
— евклидова норма вектора x-ci,
а ci - некоторый заданный вектор, называемый
центром функции. Частным случаем таких функций являются гауссовые функции вида
,
— евклидова норма вектора x-ci,
а ci - некоторый заданный вектор, называемый
центром функции. Частным случаем таких функций являются гауссовые функции вида ![]() которым
соответствуют гауссовые нейронные сети. Отметим здесь, что центры ci, обычно выбираются из входной последовательности
x[i] [36].
которым
соответствуют гауссовые нейронные сети. Отметим здесь, что центры ci, обычно выбираются из входной последовательности
x[i] [36].
Поскольку выход ![]() нейронной сети СМАС также
представляется линейной комбинацией функций рут
нейронной сети СМАС также
представляется линейной комбинацией функций рут![]() , (31), (32), то далее будем называть
функции pyr(x, x[m]),
, (31), (32), то далее будем называть
функции pyr(x, x[m]), ![]() , базисными функциями нейронной
сети СМАС. Заметим, что если исходить из представления выхода сети в виде
выражения (22), то в роли базисных функций выступает бинарная функция,
принимающая два значения: ноль и единица, так как компонентами вектора а
являются 0 и 1. Поэтому в литературе нейронная сеть СМАС и ее система базисных
, базисными функциями нейронной
сети СМАС. Заметим, что если исходить из представления выхода сети в виде
выражения (22), то в роли базисных функций выступает бинарная функция,
принимающая два значения: ноль и единица, так как компонентами вектора а
являются 0 и 1. Поэтому в литературе нейронная сеть СМАС и ее система базисных
функций иногда называется бинарной [6].
4.2. СВОЙСТВА БАЗИСНЫХ ФУНКЦИЙ НЕЙРОННОЙ СЕТИ СМАС
Рассмотрим теперь базисные функции, которые образуют ряд (31). Отметим сначала, что из принципа построения ассоциативного вектора а следует (см. пп. 2.2 и 2.4), что значение функции pyr(x, x[m]), в любой точке х равно числу общих ячеек памяти, которые соответствуют векторам х и х[n]
Поскольку вектор а(x) — М - мерный бинарный вектор, p* компонент которого равны единице, а остальные равны нулю, то очевидны первые два свойства функций pyr(x, x[m]),
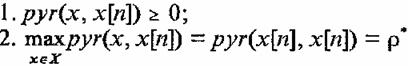 так что точку x[n] уместно назвать центром функции pyr(x, x[m]).
так что точку x[n] уместно назвать центром функции pyr(x, x[m]).
Следующие свойства не столь очевидны, как первые два. Они принципиально обусловлены алгоритмом построения вектора номеров активных ячеек m и ассоциативного вектора a по входному вектору х (см. пп. 2.2 и 2.4):

где функция Pyr(x, x[m]) задает правильную N+1 -мерную пирамиду:
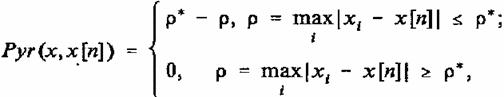
основанием которой является N-мерный гиперкуб, каждое ребро которого имеет 2p* + 1 точек и центром которого являетcя точка x[n].
Таким образом, функция pyr(x, x[m]) представляет собою вписанную в правильную (N+1)-мерную пирамиду Pyr(x, x[m]) фигуру.
5. Вид
функции, как правило, зависит от координат ее центра х[n].
При этом число различных по форме функций pyr(x, x[m])
значительно меньше числа точек ![]() на которых задана аппроксимируемая
функция у(х). В частности, в двумерном случае число различных по форме функций
равно p* более того, каждой из этих функций
можно присвоить отдельный номер, который легко вычисляется по координатам
вектора х номер функции pyr(x, x[m]) может быть задан выражением
на которых задана аппроксимируемая
функция у(х). В частности, в двумерном случае число различных по форме функций
равно p* более того, каждой из этих функций
можно присвоить отдельный номер, который легко вычисляется по координатам
вектора х номер функции pyr(x, x[m]) может быть задан выражением![]() .
.
6. В одномерном случае (N=1) базисные функции pyr(x, x[m]) представляют собой равнобедренные треугольники, которые задаются выражением
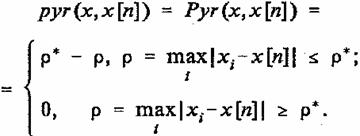 (33)
(33)
4.3. ПОСТРОЕНИЕ БАЗИСНЫХ ФУНКЦИЙ НЕЙРОННОЙ СЕТИ СМАС
В одномерном случае построение базисных функций не составляет труда, поскольку существует аналитическое выражение (33) для этой функции.
В многомерном случае аналитического выражения для базисных функций не существует. Для построения или вычисления этих функций проще всего воспользоваться нейронной сетью СМАС, пользуясь следующим определением.
ОПРЕДЕЛЕНИЕ. Базисной функцией нейронной сети СМАС является функция pyr(x, x[m]) которую воспроизводит сеть с нулевой памятью при запоминании значений функции y(x[n])=p*
Это определение следует из выражения (31) для базисной функции.
Перейдем теперь к двумерному случаю, когда множество аргументов задано
на сетке ![]() .
Этот случай представляет особый интерес, поскольку с ним связана задача
обработки изображений. Удобно ввести понятие нормированная базисная функция.
Эта функция pyrN(x, x[m]) связана с базисной функцией
соотношением pyrN(x,
x[m])= =pyr(x, x[m]) /p* Очевидно, pyrN(x[n], x[m])=1.
.
Этот случай представляет особый интерес, поскольку с ним связана задача
обработки изображений. Удобно ввести понятие нормированная базисная функция.
Эта функция pyrN(x, x[m]) связана с базисной функцией
соотношением pyrN(x,
x[m])= =pyr(x, x[m]) /p* Очевидно, pyrN(x[n], x[m])=1.
На приведенных рисунках показаны нормированные базисные функции сети при двух значениях параметра p*: p* = 2 и p* = 8. Эти функции показаны как функции непрерывного аргумента, что делает рисунки наглядными, хотя, на самом деле, функции определены только на дискретной сетке. Нормированные базисные функции представляют собой неправильные пирамиды pyrN(x, x[m]). Аргументы и, следовательно, центры х[n] функций pyrN(x, x[m]) выбраны так, чтобы нормированная базисная функция полностью находилась в области определения функции y(х), что позволяет получить полное изображение функции.
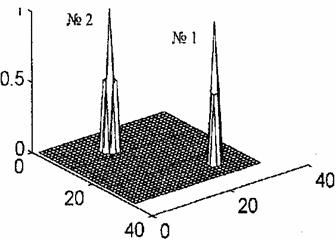
Рис. 1.
На рис. 1 показаны две нормированные базисные функции двумерной
нейронной сети СМАС при p* = 2: с центром в
точке ![]() и
с центром в точке
и
с центром в точке ![]()
В соответствии со свойством 5 число различных по форме таких функций также равно двум.
Функции повернуты вокруг своих вертикальных осей симметрии относительно друг друга на 900.
С увеличением числа активных ячеек p* усложняется структура базисных функций pyrN(x[n],x[m])=1.
На рис. 2—5 показаны все восемь нормированных базисных функций нейронной сети СМАС при p* = 8.

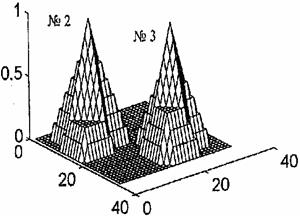
Рис. 2. Рис. 3.
На рис. 2 построены нормированные базисные функции № = 8 и № = 1 с центрами соответственно в точках x[1]=(9, 9)T и x[2]=(25, 24).
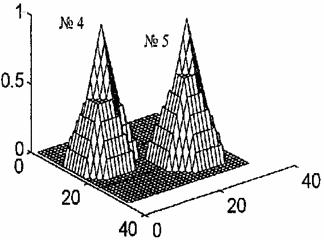
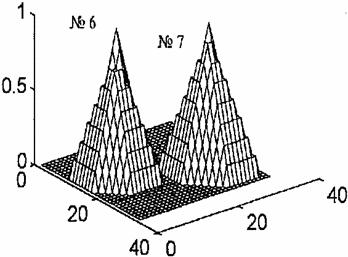
Рис. 4. Рис. 5.
Рис. 3 представляет нормированные базисные функции № = 2 и № = З с центрами соответственно в точках x[3] = (11, 9)T и x[4] = (25, 22)T Нормированные базисные функции
№= 4 и № = 5 с центрами соответственно в точках x[5] = (11, 9)Т и x[6] = (22, 25)T показаны на рис. 4. На рис. 5 построены нормированные базисные функции № = 6 и № = 7 с центрами соответственно в точках x[7] = (15, 9)T и x[2] = (24, 25)T. Базисные функции построены средствами системы Mat LAB по данным, полученным с по мощью Турбо-Паскалевской программы, которая реализует нейронную сеть СМАС.
* * *
В первой части дано описание нейронной сети СМАС, которое позволяет программировать и исследовать эту сеть. В последующей второй части будут представлены результаты обучения этой сети по запоминанию ряда функций и будет описан быстрый алгоритм обучения сети. Кроме того, будет проведено исследование влияния помех на процесс обучения и предложен способ устранения этого влияния.
Работа выполнена при частичной поддержке РФФИ, грант № 96-01-00768.
Список литературы
- Albus J.S. A new approach to manipulator control: the cerebellar model articulation controller // ASME Trans., J. Dynamic Systems, Measurement and Control. 1975. V. 97. №3. P. 220-227.
- Albus J.S. Data storage in the cerebellar model articulation controller (CMAC) // ASME Trans., J. Dynamic Systems, Measurement and Control. 1975. V. 97. №3. P. 228-233.
- Ersij E., Tolle H. A new concept for learning control inspired by brain theory // Proc. Ninth IFAC World Congress, Budapest. 1984. V. 2. P. 1039-1044.
- Tolle H., Militzer J., Ersu E. Zur Leistungsfahigheit in lernendem Regelungen // Messen, Steuern, Regeln. 1989. V. 3. 98-105.
- Tolle H., Ersij E. Neurocontrol. Learning control systems unspired by neural architectures and human problem solving strategies. Springer–Verlag, 1992, 211p.
- Brown M., Harris Ch. Neurofuzzy adaptive modeling and control. Prentice Hall, 1994, 508 p.
- Miller .W. T., Glanc F.H., Kraft L. G. CMAC: neural netvork alternative to backpropagation // Proceedindings of the IEEE. 1990. V. 78. №10. P. 1561-1567.
- Kraft L. G., Campagna D. P. A compation between CMAC neural network and two traditional adaptive control systems // IEEE Control System Magazine. Special issue on neural networks in control systems. 1990. V. 10. №3 P. 36-43.
- Беккенбах Э. Современная математика для инженеров. М.: ИЛ, 1958.
- Милитцер Ю., Паркс П. С. Свойства сходимости ассоциативной памяти в обучающихся системах управления // Автоматика и телемеханика. 1989. №2. С 158-184ю
- Аведьян Э. Д., Хормель М. Повышение скорости сходимости процесса обучения в специальной системе ассоциативной памяти // Автоматика и телемеханика. 1991. №12. С. 100-109.
- Райбман Н. С., Чадеев В. М. Адаптивные модели в системах управления. М.: Сов. Радио. 1966.
- Лелашвили Ш. Г. Применение одного итерационного метода для анализа многомерных автоматических систем // Сб. “Схемы автоматического управления”, Тбилиси: Мецниеереба. 1965. С. 19-33.
- Лелашвилли Ш. Г. Некоторые вопросы построения систематической модели многомерных объектов // Сб. “Автоматическое управление”, Тбилиси: Мецниеереба. 1967. С.59-96.
- Аведьян Э. Д. Модифицированный алгоритм Качмажа для оценки параметров линейных объектов // Автоматика и телемеханика. 1978. №5. С. 64-71.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, №5. 1997
ТЕОРИЯ НЕЙРОННЫХ СЕТЕЙ
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



