научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#10 октябрь 2004
![]() Алгоритмы обработки информации инерциально-спутниковой системы навигации
и управления летательным аппаратом
Алгоритмы обработки информации инерциально-спутниковой системы навигации
и управления летательным аппаратом
Долгушин Евгений Владимирович
средняя школа № 21, г. Раменское, 11 класс
Научный руководитель:
Рогалев Алексей Павлович,
кандидат технических наук,
главный специалист ФНПЦ «Раменское приборостроительное КБ»,
доцент кафедры «Приборы и системы ориетации,
стабилизации и навигации»
МГТУ им. Н.Э.Баумана
Современный уровень развития авиационной техники характеризуется значительным ростом требований предъявляемых к комплексам бортового оборудования (КБО) летательных аппаратов (ЛА) по точности и надежности решения задач навигации и управления ЛА. Для наиболее полного удовлетворения этих требований в настоящее время широкое применение получило комплексирование инерциальных навигационных систем (ИНС) со спутниковыми навигационными системами (СНС). Одной из главных задач комплексирования ИНС и СНС является разработка алгоритмов комплексной обработки информации навигационных систем.
Разработка алгоритмов решения задач навигации в инерциально-спутниковой навигационной системе (ИСНС) включает в себя следующие основные этапы:
Ø определение математической модели околоземного навигационного пространства и координатных трехгранников;
Ø разработка алгоритмов обработки информации инерциальной и спутниковой навигационных систем;
Ø разработка алгоритмов комплексной обработки информации инерциально-спутниковой навигационной системы.
Целью настоящей работы является анализ методов и алгоритмов решения задач инерциально-спутниковой навигационной системы, разработка вычислительных алгоритмов комплексной обработки информации ИСНС и проведение оценки их вычислительных характеристик.
1. Определение математической модели околоземного навигационного пространства и координатных трехгранников
В настоящей работе для упрощения решения задач навигации используется представление поверхности Земли в виде сферы. При этом математическая модель околоземного навигационного пространства определяется как семейство концентрических сфер. Эти концентрические сферы являются базовыми поверхностями модели навигационного пространства, центр которых совпадает с центром земного шара. Все это позволяет упростить задачу исследования методов решения задач, однако, основные результаты исследований остаются применимыми для решения общих задач навигации.
Для решения задач околоземной навигации используются ряд прямоугольных координатных трехгранников (рис.1):
Земной координатный трехгранник OXYZ: вершина трехгранника совмещена с центром Земли, ось ОZ направлена вдоль оси вращения Земли, трехгранник ОХУZ вращается вокруг оси ОZ с угловой скоростью вращения Земли U, ось OХ направлена вдоль линии пересечения экватора и гринвичского меридиана.
Инерциальный координатный трехгранник OXиYиZи: этот трехгранник не участвует в суточном вращении Земли, направление его осей фиксируется в момент включения системы навигации в рабочий режим (t=0), в этот момент инерциальный трехгранник OXиYиZи совпадает с земным координатным трехгранником OXYZ.
Для каждой точки навигационного пространства
определяется географический координатный трехгранник ОENH, ось ОН которого направлена по нормали
к земной сфере, а ее ориентация определяется географическими координатами местоположения
объекта l, j, ![]() , ось ОN направлена по касательной к меридиану на север, а ось ОЕ
– по касательной к параллели на восток.
, ось ОN направлена по касательной к меридиану на север, а ось ОЕ
– по касательной к параллели на восток.
Для каждой точки навигационного пространства определяется опорный координатный трехгранник Оxhz, ось Оz которого совпадает с осью ОН географического трехгранника, оси Оx и Оh лежат в касательной плоскости базовой поверхности навигационного пространства и повернуты относительно осей ОЕ, ОN на известный угол c:
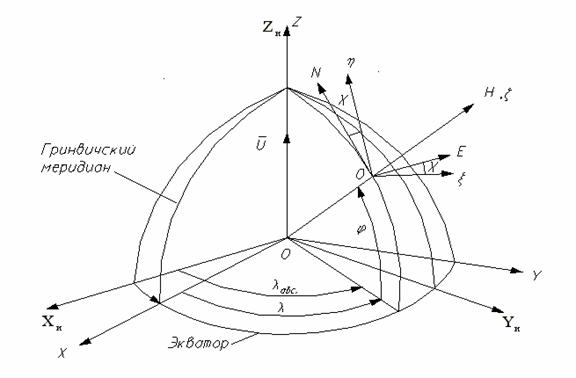
Рис.1. Определение навигационных координатных трехгранников
В
рассматриваемом навигационном пространстве существует однозначная связь между скоростью
изменения географических координат ![]() и
линейной скоростью движения объекта υЕ , υN :
и
линейной скоростью движения объекта υЕ , υN :
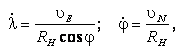
где RH=R+H, R=6371км - радиус Земли, H- высота полета.
![]() Здесь
следует заметить, что в уравнении для
Здесь
следует заметить, что в уравнении для ![]() присутствует
деление на cosj и, следовательно,
при j 90о, т.е. при приближении
к полюсу
присутствует
деление на cosj и, следовательно,
при j 90о, т.е. при приближении
к полюсу ![]() стремятся к бесконечности.
По этой причине эти уравнения не находят практического применения при решении задач
навигации.
стремятся к бесконечности.
По этой причине эти уравнения не находят практического применения при решении задач
навигации.
 |
Исключить этот недостаток возможно применением ортодромической системы координат, обеспечивающей решение проблемы «полюсов». При этом следует отметить, что применение ортодромических координат обеспечивает не только решение проблемы «полюсов», но и дает хороший аппарат для построения заданной траектории движения ЛА путем последовательного использования различных частных ортодромических координат (рис. 2).
Рис. 2. Определение ортодромических координат
Ортодромические координаты определим следующим образом. Через две заданные
точки на земном шаре ![]() и
центр Земли проведем плоскость, называемую плоскостью ортодромического экватора.
Линию пересечения данной плоскости с земным шаром называют ортодромией.
и
центр Земли проведем плоскость, называемую плоскостью ортодромического экватора.
Линию пересечения данной плоскости с земным шаром называют ортодромией.
Долгота линии пересечения плоскостей ортодромического и географического экваторов lорт и угол между этими плоскостями jвр, называемый широтой вертекса, являются параметрами ортодромии.
Определим главный ортодромический координатный трехгранник ОХортУортZорт следующим образом. Главный координатный трехгранник Земли ОХУZ повернем вокруг оси ОZ на угол lорт, затем – вокруг нового положения оси ОХ на угол jвр. Трехгранник ОХортУортZорт, полученный из трехгранника ОХУZ указанным двукратным поворотом, назовем главным ортодромическим трехгранником. Плоскость ОХортУорт называется плоскостью ортодромического экватора, а плоскость ОZортХорт - плоскостью нулевого ортодромического меридиана.
Плоскость, проходящая через ось ОZорт и заданную точку М, называется плоскостью ортодромического меридиана данной точки М. Ортодромическая долгота L точки М определяется как двугранный угол между плоскостью нулевого ортодромического меридиана и плоскостью ортодромического меридиана точки М, а ортодромическая долгота Φ точки М является углом между радиус-вектором точки М и плоскостью ортодромического экватора.
Для каждой точки М навигационного пространства определим ортодромический координатный трехгранник Оxортhортzорт, ось Оzорт которого совпадает с осью ОН(Оz), ось Оhорт лежит в плоскости ортодромического меридиана, оси Оxорт дополняет оси Оhорт, Оzорт до правого координатного трехгранника.
Преобразование географических координат (l, j) точки М в ортодромические (L, Φ ) и их обратное преобразование, а также определение угловой дальности DL между двумя точками Р1, Р2 и угла YL направления из первой точки на вторую, расчет параметров ортодромии lорт, jвр, вычисление угла ym сходимости географического и ортодромического меридианов текущей точки М осуществляются по формулам сферической тригонометрии [1], которые для рассматриваемых задач приведены к единой стандартной форме и использование которых может быть осуществлено в соответствии с типовой вычислительной схемой преобразований координат (Табл. 1).
Стандартные унифицированные формулы преобразования координат:
Таблица 1.
Типовая вычислительная схема преобразований координат
|
№№ |
Наименование сферических пересчетов |
Значение входных параметров x, y, z |
Значение промежуточных параметров V, U, W |
Значение выходных параметров P,Q |
|
1 |
Расчет DL, YL по двум точкам Р1, Р2 |
x = j1 y = j2 z = l2-l1 |
V = B1 U = B2 W = B3 |
DL = P YL = Q |
|
2 |
Расчет параметров ортодромии jвр, lорт |
x = p/2 -l1 y = p/2 - YL z = p/2 -j1 |
V = B2 U = B3 W = B1 |
jвр = P lорт = Q |
|
3 |
Расчет угла сходимости ym |
x = j y = p/2 - jвр z = lорт -l- p/2 |
V = B1 U = B2 W = B3 |
ym = Q |
|
4 |
Пересчет
|
x = jвр y = j z = p/2 +lорт-l |
V = B3 U = B1 W = B2 |
Φ=p/2 –P L= Q |
|
5 |
Пересчет
|
x = 2p-jвр y = Φ z = p/2 -L |
V = B3 U = B1 W = B2 |
j=p/2- Р l=lорт+ Q |
2. Алгоритмы обработки информации инерциальной навигационной системы
Принцип действия инерциальных навигационных систем основан на законах механики Ньютона и предполагает двойное интегрирование измеряемых ускорений на борту объекта. При этом необходимо определить проекции этих ускорений на выбранную навигационную систему координат (опорный трехгранник Oxhz). Для определения указанных проекций на борту ЛА необходимо построить навигационную систему так, чтобы оси акселерометров совпадали с осями опорного трехгранника, которые материализуются управляемой гиростабилизированной платформой в бортовой инерциальной навигационной системе.
Основные уравнения инерциальной навигации в осях опорного координатного трехгранника имеют вид [2]:

![]()
где: составляющие, соответственно, абсолютного, кажуегося и гравитационного ускорения в опорной системе координат;
Vx ,Vh,Vz - составляющие абсолютной скорости движения объекта;
wx , wh, wz - составляющие угловой скорости вращения опорного трехгранника определяются по формулам:

Эти составляющие угловой скорости используются для управления гиростабилизированной платформы, обеспечивая ее горизонтирование.
Для обеспечения интегрирования уравнений инерциальной навигации в бортовой цифровой вычислительной машине (БЦВМ) представим указанные уравнения в дискретной форме для малого интервала времени t [4, 5, 6]:

где k – номер интервала дискретности.
Начальные значения для скоростей Vx(0), Vh(0), Vz(0) определяются начальными условиями взлета.
Счисление ортодромических координат местоположения объекта L,F по данным ИНС осуществляется следующим образом. Составляющие скорости вращения опорного трехгранника Oxhz относительно Земли ux , uh, uz определяются по формулам:

где составляющие скорости вращения Земли U в осях опорного трехгранника Ux, Uh, Uz вычисляются по формулам:
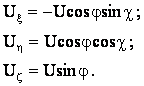
Затем определяют ортодромические составляющие относительной скорости вращения опорного трехгранника Oxортhортzорт по формулам:

Уравнения для скорости изменения ортодромических координат имеют вид:

которые в дискретной форме могут быть представляются в виде:

где k – номер интервала дискретности.
Начальные значения ортодромических координат L(0), F(0) и угла сходимости меридианов ym0 определяются в соответствии с таблицей 1 по стандартным унифицирован-ным формулам преобразования координат. Начальное значение угла ориентации A(0) определяется по формуле:
![]()
Определение географических координат l, j осуществляется пересчетом ортодромических координат L, F в соответствии с таблицей 1 по указанным формулам.
Счисление высоты полета Н осуществляется по формуле:
![]()
где Н(0) – начальное значение высоты местоположения ЛА над уровнем земного эллипсоида.
3. Алгоритмы обработки информации спутниковой
навигационной системы
В настоящей работе в качестве расчетной принята упрощенная модель гипотетической СНС, близкой по своим основным характеристикам к отечественной системе ГЛОНАСС [3].
Принцип действия спутниковой навигационной системы (СНС) основан на радиоизмерении на борту летательного аппарата дальностей (Рис. 3) до соответствующих навигационных искусственных спутников Земли.
Параметры движения навигационных искусственных спутников (НС) Земли являются известными функциями времени, что обеспечивается соответствующей организацией движения НС. Одновременно 24 навигационных искусственных спутника Земли (НС) движутся по трем круговым орбитам, восходящие узлы которых сдвинуты на 120°, а их угловое наклонение относительно экваториальной плоскости составляет величину 60°. Спутники движутся по орбитам равномерно с угловым интервалом 45° с постоянным периодом обращения 12 часов.
Для решения навигационной задачи необходим прием измерений от трех НС, т.е. рабочее созвездие спутников, находящихся в зоне радиовидимости в каждый момент времени должно включать в себя не менее трех навигационных спутников.
 |
Рис. 3. Общая структура спутниковой навигационной системы
Измерив дальности до трех навигационных искусственных спутников Земли, гринвичские координаты которых известны (Xi , Yi , Zi, где i=1,2,3), можно получить систему трех уравнений [3]:
D1 = ((Xс - X1)2 + (Yс - Y1)2 + (Zс - Z 1)2)0.5;
D2 = ((Xс - X2)2 + (Yс - Y2)2 + (Zс - Z 2)2)0.5;
D3 = ((Xс - X3)2 + (Yс - Y3)2 + (Zс - Z 3)2)0.5.
После соответствующих преобразований этих уравнений получим гринвичские координаты самолета Xс,Yс,Zс .
По декартовым координатам Xс, Yс, Zс можно определить географические координаты самолета: долготы lс, широты jс и высоты Нс, - по формулам:

где R - радиус земной сферы.
Координаты самолета, полученные по данным спутниковой навигационной системы, используются в алгоритмах комплексной обработки информации ИСНС.
4. Алгоритмы комплексной обработки информации инерциально-спутниковой навигационной системы
В соответствии с принципом действия инерциальные системы навигации имеют высокую точность определения навигационных параметров при непродолжительной их работе, но обладают свойством накопления ошибок в течение длительного времени работы. Информация ИНС имеет непрерывный характер. Позиционные спутниковые радионавигационные системы обладают высокой точностью определения координат, практически независящей от времени работы системы, но их выходные данные имеют прерывистый характер. На основании указанных и ряда других свойств при комплексировании навигационных систем инерциальные системы используются в качестве основного датчика навигационной информации, а позиционные СНС – в качестве средств коррекции ИНС. В промежутках между коррекциями инерциальная система, выполняя роль «активной памяти», продолжает определение навигационных параметров с использованием результатов предыдущих коррекций.
В настоящее время для комплексной обработки информации (КОИ) инерциально-спутниковой навигационной системы широкое применение получил метод Калмановской фильтрации [4, 5, 6]. Алгоритм КОИ, построенный на основе метода калмановской фильтрации, вырабатывает оценки ошибок ИНС динамически с учетом текущих параметров движения самолета, позволяет использовать информацию с любой дискретностью по мере ее получения. При одновременном получении нескольких независимых измерений процедура Калмана позволяет использовать их путем последовательной обработки каждого отдельного измерения, что позволяет снизить потребный объем памяти БЦВМ для реализации алгоритмов коррекции.
Алгоритм комплексной обработки информации, построенный на основе метода кал-мановской фильтрации, в векторно-матричном форме может быть представлен в виде [5, 6]:
![]()
![]()
![]()
![]()
![]()
где:
F
– переходная матрица для дискретных уравнений ошибок ИНС размерности (n´n); ![]() -
векторы прогноза и оценки ошибок ИНС размерности (n´1); Н - матрица связи вектора измерения Z c вектором
ошибок Х; Z – вектор измерений ошибок ИНС; K,P,R – матричные параметры алгоритмов
КОИ.
-
векторы прогноза и оценки ошибок ИНС размерности (n´1); Н - матрица связи вектора измерения Z c вектором
ошибок Х; Z – вектор измерений ошибок ИНС; K,P,R – матричные параметры алгоритмов
КОИ.
Элементы вектора Z определяется по формулам:
![]()
где l, j и lс, jс - координаты местоположения, полученные по данным ИНС и СНС, соответственно; c- угол ориентации гиростабилизированной платформы ИНС.
Переходная матрица системы F имеет большое количество нулевых и единичных элементов [6]. Для рассматриваемого в настоящей работе варианта системы из 400 элементов переходной матрицы F[20, 20]:
- 45 элементов ¹ 0, из них 20 элементов = 1;
- 355 элементов = 0.
Исключая умножение на нули и единицы и сложение с нулями при реализации алгоритмов КОИ, получим следующую вычислительную модель алгоритмов комплексной обработки информации инерциально-спутниковой навигационной системы.
Прогнозирование вектора оценок ошибок ИНС вектора состояния:


![]() Прогнозирование
матрицы P фильтра
Прогнозирование
матрицы P фильтра
Выполнив умножение матрицы F на матрицу Р, мы получим элементы матрицы В:

![]()

![]()
![]() j = 1, 2, …, 20.
j = 1, 2, …, 20.
Далее, если выполнить умножение матрицы В на FT, то получим элементы матрицы
![]() .
.

![]()
![]()

i = 1, 2, …, 20.
Оценивание вектора состояния Х и матрицы Р фильтра Калмана

![]()
![]()
(i = 1, 2, …, 20; j = 1, 2, …, 20);
(m = 1, 2).
После обработки первого измерения осуществляется присвоение прогнозируемым
компонентам вектора состояния![]() и элементам матрицы ковариации
и элементам матрицы ковариации ![]() соответствующих оцененных параметров:
соответствующих оцененных параметров:

(i = 1, 2, …, 20; j = 1, 2, …, 20).
После обработки второго измерения прогноз вектора состояния ![]() и матрицы ковариаций
и матрицы ковариаций ![]() осуществляется в соответствии с ранее полученными формулами.
осуществляется в соответствии с ранее полученными формулами.
Вычислительный алгоритм фильтра Калмана, обеспечивает оценивание погрешностей ИНС с использованием данных спутниковой навигационной системы. Полученные оценки погрешностей ИНС используются для коррекции ошибок инерциальной навигационной системы.
5. Анализ вычислительных потребностей алгоритмов КОИ
Анализируя уравнения алгоритмов КОИ
можно заметить, что обработка информации требует выполнения большого числа операций
над матрицами и векторами. При этом следует отметить, что объем вычислений на один
такт работы БЦВМ (получение значений ![]() по
известным значениям
по
известным значениям ![]() ) определяются,
прежде всего, размерностями входящих в уравнения фильтра матриц и векторов. В табл.
2 представлены вычислительные характеристики алгоритмов КОИ для векторно-матричной
формы (вариант 1) и для расчетной модели, полученной в настоящей работе с учетом
преобладающего большинства нулевых и единичных элементов переходных матриц F и Н (вариант2),
для основных вычислительных операций умножения и сложения.
) определяются,
прежде всего, размерностями входящих в уравнения фильтра матриц и векторов. В табл.
2 представлены вычислительные характеристики алгоритмов КОИ для векторно-матричной
формы (вариант 1) и для расчетной модели, полученной в настоящей работе с учетом
преобладающего большинства нулевых и единичных элементов переходных матриц F и Н (вариант2),
для основных вычислительных операций умножения и сложения.
Таблица 2
|
Перемен-ная |
Число умножений |
Число сложений | ||
|
Вариант 1 |
Вариант 2 |
Вариант 1 |
Вариант 2 | |
|
|
n2 = 400 |
25 |
n(n-1) = 380 |
25 |
|
|
2n3 = 16000 |
2×25×n=1000 |
2n2(n-1)=15200 |
2×25×n=1000 |
|
K(k) |
4(n2+n)=1680 |
2(n+1)=42 |
2(n-1)(2n+1)=1558 |
2 |
|
|
4n = 80 |
2n=40 |
4n = 80 |
2(n+1)=42 |
|
|
4n2 = 1600 |
2n2 = 800 |
2n(2n-1)=1560 |
2n2 = 800 |
|
S= |
19760 |
1907 |
18778 |
1869 |
Выводы
1. В работе дано краткое определение задачи навигации и модели околоземного навигационного пространства, выполнен анализ метода инерциальной навигации и метода спутниковой радионавигации, алгоритмов комплексной обработки информации инерциально-спутниковой навигационной системы, выявлены пути повышения точности определения навигационных параметров и оптимизации вычислительных характеристик алгоритмов обработке информации ИСНС.
2. Разработана унифицированная вычислительная схема преобразования ортодромических координат, обеспечивающая снижение потребностей вычислительных ресурсов БЦВМ. Разработаны алгоритмы решения задачи инерциальной навигации с использованием этой вычислительной схемы.
3. Разработаны расчетная модель и алгоритмы комплексной обработки информации инерциально-спутниковой навигационной системы с учетом преобладающего большинства нулевых и единичных элементов переходных матриц алгоритмов КОИ, обеспечивающие значительное снижение потребностей вычислительных ресурсов бортового компьютера для их реализации.
4. Разработаны вычислительные алгоритмы и программы обработки информации комплексной инерциально-спутниковой навигационной системы и проведена оценка их вычислительных характеристик.
5. Данные, представленные в таблице 2, подтверждают, что вычислительные характеристики алгоритмов обработки информации ИСНС, полученных в настоящей работе, на порядок превосходят соответствующие характеристики исходных алгоритмов в векторно-матричной форме.
Список литературы
1. Бронштейн И.Н., Семендяев К.А. Справочник по математике. - М.: Наука, 1965.
2. Бромберг П.В. Теория инерциальных систем навигации. - М.: Наука, 1979.
3. Глобальная спутниковая радионавигационная система ГЛОНАСС / Под ред. В.Н.Харисова, А.И.Петрова, В.А.Болдина. – 2-е изд. исправ. – М.: ИПРЖР, 1999.
4. Ривкин С.С., Ивановский Р.И., Костров А.В. Статистическая оптимизация навигационных систем. - Л.: Судостроение, 1976.
5. Бабич О.А. Обработка информации в навигационных комплексах. - М.: Машиностроение, 1991.
6. Рогалев А.П. Об алгоритмах позиционной радиокоррекции инерциальных навигационных систем // Науч.-метод. матер. по системам навигации и управления летательными аппаратами / Под ред. О.А.Бабича. - М.: ВВИА им. Н.Е.Жуковского, 1981.
7. Рогалев А.П., Бабиченко А.В. Методы и алгоритмы интеграции данных инерциально-спутниковых навигационных систем. // Авиакосмическое приборостроение. – М.: Научтехлитиздат. - № 4. - 2002.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||