научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#9 сентябрь 2004
Д.И. Батищев, проф. ННГУ (Россия);
Э.Д. Гудман, проф. Мичиганского университета (США);
ИЛ. Норенков, проф. МГТУ им. Н.Э. Баумана (Россия);
М.Х. Прилуцкий, проф. ННГУ (Россия)
УДК б81.3.015
Метод декомпозиций для решения комбинаторных задач упорядочения
и распределения ресурсов
В качестве примера использования предлагаемого подхода выбрана комбинаторная задача теории расписаний, являющаяся обобщением известной задачи Гиффлера-Томпсона [1], в которой оценка качества решения аддитивно определяется тремя составляющими: затратами на выполнение работ на машинах, затратами на переналадки машин и штрафными санкциями, связанными с нарушениями директивных сроков выполнения работ. Рассматриваемая схема решения исходной задачи названа методом декомпозиций. Она включает две группы алгоритмов:
генетические алгоритмы решения задачи упорядочения [2] - для определения последовательности работ;
эвристические алгоритмы [3] построения расписаний с учетом найденных последовательностей.
1. Содержательная постановка задачи
Рассматриваемая задача является достаточно общей в классе задач теории расписаний. В ней учитываются временные и стоимостные затраты на выполнение работ на машинах (серверах), затраты на переналадки машин, затраты, связанные с нарушениями ограничений на сроки выполнения работ, а также многостадийность производственного процесса, характеризуемая специальными технологическими и организационными условиями, предъявляемыми к искомым расписаниям.
К технологическим условиям относятся следующие:
• каждая работа состоит из нескольких (не менее одной) одинаковых операций;
• работы распределены по группам так, что длительности выполнения работ на машинах зависят не от номеров работ, а от номеров групп, к которым работы принадлежат;
• работы распределены по семействам так, что длительности переналадок зависят не от номеров работ, а от номеров семейств, к которым работы принадлежат;
• работа для своего завершения должна пройти обработку на нескольких стадиях, причем на каждой стадии используется одна из взаимозаменяемых машин;
• каждая машина используется на одной конкретной стадии;
• технологические маршруты для всех работ одинаковы, поэтому предполагается, что каждая работа должна пройти обработку последовательно, начиная с первой и заканчивая последней стадией;
• каждая машина одновременно не может выполнять более одной работы или одновременно выполнять работу и проходить переналадку;
• каждая работа обслуживается на машине без перерывов до окончания всех входящих в нее операций;
• выполнение работы на очередной стадии может начаться сразу же после того, как на предыдущей стадии закончится хотя бы первая операция этой работы;
• переналадка машины под работу i на очередной стадии может осуществляться во время выполнения этой работы на предыдущих стадиях.
К организационным условиям относятся следующие:
• окончание выполнения работы на последней стадии должно завершиться не позднее заданных для этой работы контрольного и более позднего директивного сроков, в противном случае на систему накладываются штрафные санкции, размер которых в случае нарушения директивных сроков больше, чем от нарушения контрольных сроков, и зависит лишь от номеров работ и не зависит от длительностей нарушений заданных ср окон.
Возникающая здесь задача заключается в определении такого расписания, в котором работы закрепляются за машинами и определяется порядок выполнения работ, причем суммарная стоимость расписания, определяемая суммарными затратами на выполнение работ на машинах, на переналадки машин и на выплаты штрафов, должна быть минимальной.
2. Математическая формулировка задачи
2.1 Исходные параметры математической модели
В дальнейшем мы будем пользоваться следующими обозначениями:
i= 1,
..., m -
номера работ, j
= 1, ...n
- номера машин, k
= 1,..s
-номера стадий,
 i
–число операций в i-й работе; у(а) - номер
семейства, к которому принадлежит работа a,
i
–число операций в i-й работе; у(а) - номер
семейства, к которому принадлежит работа a,
Параметры, описывающие количественные характеристики рассматриваемого технологического процесса, считаются заданными и включают в себя следующие постоянные величины:
• число машин, используемых на каждой стадии;
время выполнения работы i на j-й машине (зависит не от номера работы, а от номера группы, к которой принадлежит работа i);
• время переналадки j-й машины на выполнение работ семейства b2, если до этого на ней выполнялись работы другого семейства b1;
• денежные затраты за единицу времени выполнения работ на j-й машине;
• денежные затраты за единицу времени переналадки
машины для каждой пары работ разных семейств.
Требуется построить допустимое расписание выполнения m работ на n машинах для данного технологического процесса, которое для каждой i-й работы (i = 1, 2 m) и каждой k-й стадии (k = 1, 2, ..., s) указывает номер машиныj (j = 1, 2, ..., n) и номера тактов начала Yij и завершения Zij выполнения i-й работы.
2.2. Варьируемые параметры математической модели
Определению подлежат переменные Xij, Yij и Zij для каждой стадии, где Хij=1, если работа i будет выполняться на машинеj, Хij=0 в противном случае; Yij и Zij целые числа.
2.3. Ограничения математической модели
Связи между исходными и варьируемыми параметрами формализуются в виде системы как линейных, так и нелинейных ограничений, среди которых существенно нелинейными являются ограничения, связанные с тем, что начало выполнения работы i на машине j стадии k может наступить лишь в следующем такте после завершения на этой стадии предшествующей ей работы и с учетом переналадки с работы семейства у(u) на работу семейства у(i):
 ,
,
где Guij — длительность переналадки с выполнения работы семейства y(u) на выполнение работы семейства у(i) на j-й машине [при у(i) = у(u) время наладки на выполнение работы семейства у(i) равно 0] Tir — длительность выполнения одной операции работы i на машине r предыдущей стадии. Для первой стадии принимается Yir=0.
2.4. Формализованное представление критериев оптимальности
Частными критериями оптимальности являются следующие.
Суммарный штраф за нарушения заданных сроков:
 ,
,
где суммируются только члены с положительными разностями Zij-Ki и Zij-Di и Zij равно времени окончания обслуживания работы на последней стадии; К — контрольный срок выполнения работы i; C1i - штраф за нарушение контрольного срока Ki; Di — директивный срок выполнения работы i; С2i —штраф за нарушение директивного срока работы i; Di>Ki>0 — целые.
Суммарные затраты на переналадку оборудования:

где Wuij, — затраты на единицу времени переналадки машины j с выполнения работы семейства у(u) на выполнение работы семейства у(i). Суммирование проводится для всех пар смежных работ.
Суммарные затраты на выполнение работ на машинах:
 ,
,
где Еj — затраты за единицу времени выполнения работы на j-й машине.
Обобщенный критерий оптимальности:
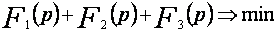 ,
,
3. Исследование математической модели
Поставленная задача является задачей дискретной оптимизации с нелинейными ограничениями и нелинейным (из-за нелинейных составляющих F1(p) и F2(p)) обобщенным критерием F(p). Она относится к классу NР - трудных задач, так как в ее рамках может быть поставлена, например, задача [TP11] «Расписание с индивидуальными директивными сроками», которая при n > 3 (n — количество машин) является NР - трудной (см. [4] стр. 306). для ее решения необходимо применять приближенные процедуры, сравнивая значения критерия приближенных решений с оценками значения критерия. Для получения оценок, необходимых для организации вычислительных процедур для задачи дискретной оптимизации, введем следующие обозначения:
Hv(p)
— значение нижней оценки для v-го
частного критерия задачи, y=1,2,3,Hv(p)
<=
 Fv(p),
где П множество всех допустимых расписаний.
Fv(p),
где П множество всех допустимых расписаний.
Определение величины H1(p).
Пусть
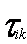 —
минимально возможное время выполнения работы i на
k-й стадии. Рассмотрим задачу 1.
—
минимально возможное время выполнения работы i на
k-й стадии. Рассмотрим задачу 1.
Пусть Q(j,s) — множество номеров работ, выполнение которых происходит на j-й машине последней s-й стадии, т.е. Q(j,s) — подмножество множества {1,2,...,m}.
Требуется определить такие множества Q(j,s),j=1,…,n, для которых выполняется условие
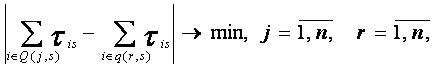
где
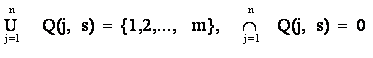
В такой постановке задача 1 является известной задачей о камнях (случай разбиения кучи камней на n куч близких весов). Она относится к классу NP - трудных, однако для этой задачи существует хороший приближенный алгоритм, применение которого позволяет быстро находить приемлемое для искомых оценок решение. Алгоритм заключается в следующем.
Все работы упорядочиваются по неубыванию величин τis.
Первоначально множества Q(j,s)
определяются как пустые. Каждому множеству
Q(j,s)
присваивается характеристика
 .
.
Очередная работа добавляется в то множество из Q(j,s), для которого меньше величина V(j,s).
Пусть Q(j,s),j=1,2,…,n — решение задачи 1 и Т=max ∑τis. Найдем величину
j=1,n
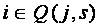

Величина W
определяет минимально возможное время завершения выполнения всех работ. Пусть
P — множество работ, для которых
Ki<W;
R —
множество работ, для которых Dj
< W. Тогда

— нижняя оценка для частного критерия F1(p)
Определение величины Н (р).
Пусть g(k)
— минимальное время наладки любой машины на любую работу на k-й
стадии. Тогда
 —
нижняя оценка для частного критерия F1(p)
—
нижняя оценка для частного критерия F1(p)
Определение величины Н3 (p).
Нижняя оценка для частного критерия F3(p)

где jk — множество номеров машин, относящихся к k-й стадии.
4. Алгоритмы решения задачи
4.1. Метод декомпозиций
4.1.1. Алгоритмы определения последовательностей работ
В результате работы алгоритмов определяются
последовательности, задающие приоритеты работ по отношению к ресурсам,
необходимым для выполнения работ. В основу алгоритмов заложен эволюционно -
генетический подход, позволяющий из m! различных
перестановок получать такие, которые дают возможность строить достаточно хорошие
расписания. В предлагаемых алгоритмах перестановка
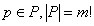 ,
где Р — множество всех перестановок из m чисел,
задается с помощью генотипа, который отвечает естественным условиям
допустимости: полноте (генотип содержит номера всех работ) и индивидуальности
(генотип не содержит одинаковых номеров работ). При заданных начальных
популяциях используются стандартные для генетических алгоритмов процедуры:
кроссинговер, мутации, естественный отбор, проверка условий окончания процесса
эволюции популяций и др. [5]. Особенности рассматриваемой задачи главным образом
сказываются на процедурах генерации начальных популяций. Опишем две такие
процедуры.
,
где Р — множество всех перестановок из m чисел,
задается с помощью генотипа, который отвечает естественным условиям
допустимости: полноте (генотип содержит номера всех работ) и индивидуальности
(генотип не содержит одинаковых номеров работ). При заданных начальных
популяциях используются стандартные для генетических алгоритмов процедуры:
кроссинговер, мутации, естественный отбор, проверка условий окончания процесса
эволюции популяций и др. [5]. Особенности рассматриваемой задачи главным образом
сказываются на процедурах генерации начальных популяций. Опишем две такие
процедуры.
Процедура 1. Определение последовательности работ по временным характеристикам. Определяются минимально возможные времена Li завершения выполнения работ:
а) в случае, когда работа включает в себя одну операцию,
 где
где
 ;
;
б) в случае, когда работа содержит несколько операций (yi >= 2),

По найденным величинам Li, определяются значения а(i), характеризующие долю “резерва” времени работы i по отношению к ее директивному сроку:
a(i)=(Di-Li)/Di.
Искомый список работ строится с использованием найденных величин.
З а м е ч а н и е. Процедура 1 при небольших изменениях позволяет генерировать и другие перестановки, для чего в качестве величин а(i) могут быть выбраны, например,
a(i)=(Di-Li)2/Di.
В этом случае в большей мере учитываются штрафы за нарушение директивных сроков и в меньшей степени
— затраты на выполнение работ. В случае, когда штрафы за нарушение директивных сроков значительны и превосходят затраты на выполнение работ, в качестве величин а(i) могут быть выбраны Di,.
Процедура 2. Определение последовательности работ по стоимостным характеристикам. Определяются минимально возможные затраты Ri, на выполнение работ
 .
.
По найденным величинам Ri определяются значения b(i), характеризующие долю Ri по отношению к общим минимально возможным затратам

Искомый список работ строится с использованием найденных величин.
4.1.2. Прямой алгоритм построения расписания выполнения работ
Шаг 1. Определение вспомогательных параметров.
Используя минимальные времена выполнения работ, определить минимальные времена выполнения работ на всех стадиях, а по ним минимальные времена ti- возможно завершения выполнения работ.
Определить величину
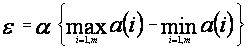
где α— управляемый параметр; 0 < α < 1— доля, определяющая множество работ, из которых выбирается очередная работа для включения в строящееся расписание. В случае, когда α=0, это множество вырождается и включает в себя лишь одну работу — самый быстрый режим работы; в случае, когда α=1, множество включает в себя все оставшиеся не рассмотренными работы — самый медленный и самый точный режим работы.
Определить затраты на выполнение работ на стадиях и по ним — минимально необходимые затраты Ri на выполнение работ на всех стадиях. Найти усредненную величину N затрат на одну работу. Найти усредненную величину М штрафов за нарушение работами контрольных (мягких) сроков.
Шаг 2. Определение списка работ. Если процент усредненных штрафов по отношению к усредненным затратам γ=M*100/N достаточно велик (например, больше 25 %), то все работы упорядочиваются по контрольным срокам, а если несколько работ имеют одинаковые контрольные сроки, то эти работы лексикографически упорядочиваются по величинам а(i) — на минимум, по директивным срокам — на минимум, далее — в произвольном порядке, например, по возрастанию номеров работ. Если γ — небольшая величина, то работы лексикографически упорядочиваются по величинам а(i) - на минимум, по контрольным срокам — на минимум, по директивным срокам на минимум, далее — в произвольном порядке, например, по возрастанию номеров работ. На основании введенного упорядочения определяется список работ.
Шаг 3. Решающие процедуры.
Берем первую работу из списка (пусть ее номер
r) и определяем величину

Строим множество работ
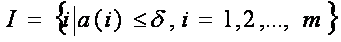 .
.
Рассмотрим три варианта решающих процедур.
Первый вариант (глобальный
одношаговый). для каждой работы из множества I подсчитываем минимальные
суммарные затраты Qi
, связанные с включением этой работы в строящееся расписание, начиная с первой
стадии. При этом работа ставится для выполнения на те машины, которые
обеспечивают минимально возможное значение
Qi
. При определении величин
Qi
необходимо учитывать все составляющие затраты от включения
работы i в расписание затраты на выполнение работ, затраты на переналадки
машин и затраты, связанные с нарушением контрольных и директивных сроков.
Находим величину
 —
затраты, превосходящие минимально необходимые. Включаем в строящееся расписание
работу p=arg
min Vi и исключаем ее из списка
работ.
—
затраты, превосходящие минимально необходимые. Включаем в строящееся расписание
работу p=arg
min Vi и исключаем ее из списка
работ.
Если список работ пуст, алгоритм заканчивает работу. Если список работ не пуст, переходим к шагу 3.
Второй вариант (локальный многошаговый). для каждой перестановки из элементов множества I подсчитываем минимальные суммарные затраты, связанные с включением этих работ в строящееся расписание в порядке, определенном соответствующей перестановкой. Первая работа перестановки, которая приносит минимальные затраты, включается в расписание и исключается из списка работ.
Если список работ пуст, алгоритм заканчивает работу. Если список работ не пуст, переходим к шагу 3.
Третий вариант (глобальный многошаговый). Для каждой перестановки из элементов множества I строим полное расписание работ, в котором первыми идут работы в порядке, определенном соответствующей перестановкой, а все остальные работы следуют в порядке, определенном списком работ. Подсчитываем полную стоимость полученного расписания. Первая работа перестановки, соответствующей расписанию минимальной стоимости, включается в строящееся расписание и исключается из списка работ.
Если список работ пуст, алгоритм заканчивает работу. Если список работ не пуст, переходим к шагу 3.
З а м е ч а н и е. Все три варианта алгоритма работают по принципу жадных алгоритмов. Это обусловлено тем, что выбранная на очередном шаге работа закрепляется в строящемся расписании и при дальнейшей работе алгоритма из расписания исключена быть не может.
Время решения задачи различными вариантами алгоритма зависит от мощности множества I. Если nr — число машин на стадии r, r = 1,2,…,s, то число вариантов выбора работ и закрепления их за конкретными машинами по первому варианту определяется величиной
 ,
где
,
где

В случае, если определять множества I при условии α=0, т.е. мощность множества I на любом шаге работы алгоритма равна 1, то расписание будет построено за m шагов, причем на каждом шаге будут проверяться Q вариантов, а общее число проверяемых вариантов будет определяться величиной H1=m*Q. В случае, когда выбирается α=1, на каждом шаге необходимо проверять варианты для каждой работы из всех оставшихся не включенными в расписание. Общее число проверяемых вариантов определяется в этом случае величиной
 .
.
Для второго и третьего вариантов, когда предлагается
рассматривать на каждом шаге
 частичных
или полных перестановок (в зависимости от мощности ЭВМ и времени, выделенного на
решение задачи), можно ввести еще один управляющий параметр алгоритма
h и на каждом
шаге проверять: ׀I׀<h+1?
Если да, то алгоритм просматривает все
частичных
или полных перестановок (в зависимости от мощности ЭВМ и времени, выделенного на
решение задачи), можно ввести еще один управляющий параметр алгоритма
h и на каждом
шаге проверять: ׀I׀<h+1?
Если да, то алгоритм просматривает все
 вариантов.
Если ׀I׀
> h,
можно ограничиться рассмотрением лишь h!
вариантов. Тогда оценка работы алгоритма по второму и третьему вариантам
(количество построенных наборов из элементов — для второго варианта и количество
построенных расписаний — для третьего варианта) будет определяться величиной
h!хm,
где m —
число работ.
вариантов.
Если ׀I׀
> h,
можно ограничиться рассмотрением лишь h!
вариантов. Тогда оценка работы алгоритма по второму и третьему вариантам
(количество построенных наборов из элементов — для второго варианта и количество
построенных расписаний — для третьего варианта) будет определяться величиной
h!хm,
где m —
число работ.
4.1.3 .двойственный алгоритм построения расписания выполнения работ
Для решения поставленной задачи может быть использована идеология двойственности, позволяющая по исходной задаче построить ее двойственный аналог, затем решить двойственную задачу, а полученное “двойственное” расписание затем преобразовать в решение исходной задачи.
В статье предложена достаточно универсальная схема исследования и приближенного решения 1 трудных задач дискретной оптимизации, основанная как на традиционно используемых для таких задач эвристических приемах, так и на применении совместно с эвристиками эволюционно-генетического подхода, адаптированного к особенностям рассматриваемых задач. Предложенный метод декомпозиции синтезирует на основе эвристических алгоритмов достаточно представительный набор допустимых решений, выступающих в качестве начальных хромосом для генетического алгоритма. Кроме изложенного метода декомпозиций, авторы исследовали также схему решения, названную методом комбинирования эвристик [6]. Метод заключается в применении на каждом шаге синтеза расписаний наилучшей из множества «быстрых» эвристик, каждая из которых строит допустимое расписание, а поиск оптимальной комбинации эвристик реализуется, с помощью генетических алгоритмов.
Метод комбинирования эвристик, а также примеры решения многостадийных задач теории расписаний, полученные с использованием предлагаемых подходов, станут предметом следующей статьи.
Список литературы
1. Giffler B., Thompson G.L. Algorithms for solving production-scheduling problems, Operat. Res. 12, N2, 1964. P. 305-324/
2. Батищев Д.И., Власов С.Е., Булгаков И.В. Решение задачи «слепого» упорядочивания с помощью генетических алгоритмов. // Тр. конф. по генетическим алгоритмам. М. 1996.
3. Прилуцкий М.Х. Оптимизация многостадийных процессов // Тез. докл. Международной конф. “Проблемы оптимизации в механике деформируемого твердого тела”, Н.Новгород, 1995. С. 41.
4. Гэри М., Джонсон Д. Вычислительные машины й труднорешаемые задачи. М.: Мир, 1982. 416 с.
5. Батищев Д. И. Генетические алгоритмьг решения экстремальных задач: Учеб, пособие. Воронеж. гос. техн. ун-т; Нижегородский гос. ун-т. Воронеж, 1995, 69 с.
6. Норенков И.П. Генетические алгоритмы синтеза расписаний и планов // «Техника, экономика». Сер. «Автоматизация проектирования». М.: ВНИИ межотраслевой информации, 1995. Вып. 1—2.С. 11—15.
Статья опубликована в журнале "Автоматизированное проектирование" №1 1997 год,
рубрика в журнале «Принятие проектных решений и методы структурного синтеза»
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



