научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2012
DOI: 10.7463/0912.0453581
УДК 621.396
Россия, МГТУ им. Н.Э. Баумана
Введение
Последние десятилетия характерны широким применением систем синхронизации. Наибольшее распространение системы синхронизации нашли в связи, в навигационных системах (GPS, Galileo и Глонасс), радиосвязи, следящих системах, для синхронизации OPERA и CERNи т.д.
Внедрение спутниковых радионавигационных и радиосвязных систем породили повышенный интерес к системам синхронизации, к их точности и помехозащищенности.
Все эти системы работают в условиях воздействия помех [1-3].
Дальнейшее усовершенствование систем синхронизации за счет улучшения конструктивных и технологических решений имеет предел, вызываемый воздействием флуктуаций и помех естественного и искусственного происхождения.
Помехоустойчивости систем синхронизации посвящен ряд работ [1-3].
В данной статье путем анализа фазовых портретов получены уравнения захвата за сигнал и захвата за гармоническую помеху.
1. Влияние гармонической помехи на систему ФАП первого порядка
Рассмотрим функциональную схему ФАП первого порядка, когда на фазовый детектор (ФД) воздействует смесь сигнала и гармонической помехи (рис. 1) [4]
![]()
![]()
где Ас, Ап – соответственно амплитуды колебаний сигнала и помехи; φс, φп – фазы колебаний соответственно сигнала и помехи детектируемая ФД в момент времени t1; t1,c– время.
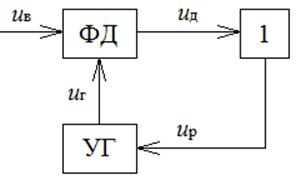
Рис. 1 Функциональная схема ФАП первого порядка
Сигнал управляемого генератора (УГ) зададим в виде
![]()
для которого справедливо дифференциальное уравнение
 (1)
(1)
где Аг – амплитуды колебаний УГ; φг – фазы колебаний УГ в момент времени t1; u(t1) – напряжение на входе УГ; kг – коэффициент передачи УГ; ω0 – собственная частота УГ.
Напряжение на выходе ФД имеет вид
![]() (2)
(2)
где kу – коэффициент усиления ФД
В результате перемножения из уравнения (2) получим

Поскольку система является узкополосной, то, очевидно, можно отбросить два последних слагаемых.
Введем новые переменные
![]()
![]()
Тогда с учетом (1) получим
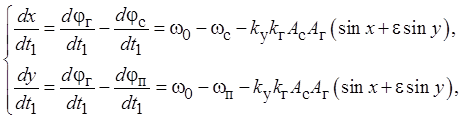
где ![]() – отношение помеха/сигнал;
– отношение помеха/сигнал; ![]()
![]()
![]() – сигнальная расстройка по частоте;
– сигнальная расстройка по частоте; ![]() – помеховая расстройка по частоте.
– помеховая расстройка по частоте.
Введем время ![]() В результате система дифференциальных уравнений примет вид
В результате система дифференциальных уравнений примет вид
 (3)
(3)
где ![]()
![]()
Рассмотрим фазовое пространство полученной системы дифференциальных уравнений. Во-первых, можно заметить, что отсутствуют точки равновесия. Если положить ![]() то получим
то получим
 (4)
(4)
По уравнению (4) можно сделать вывод, что точки равновесия возможны лишь в случае ![]() , что по предположению не выполняется. Таким образом, фазовые траектории данной системы не пересекаются.
, что по предположению не выполняется. Таким образом, фазовые траектории данной системы не пересекаются.
Так же фазовое пространство является неизменным, откуда следует ![]() и
и ![]() . В связи с выше рассмотренным достаточно рассмотреть лишь один фрагмент фазовой плоскости (рис. 2), например
. В связи с выше рассмотренным достаточно рассмотреть лишь один фрагмент фазовой плоскости (рис. 2), например ![]() Для всех остальных значений xи y данный фрагмент будет периодически повторяться.
Для всех остальных значений xи y данный фрагмент будет периодически повторяться.

Рис. 2 Фрагмент фазового пространства в пределах ![]()
Для исследования поведения фазовых траекторий выделим на фазовой плоскости области с постоянным направлением изменения xи y. Границами таких областей являются ![]() и
и ![]() . Отсюда из уравнения (4) для нижней полуплоскости bприведенной на рис. 2 получаем
. Отсюда из уравнения (4) для нижней полуплоскости bприведенной на рис. 2 получаем

Для верхней полуплоскости a(рис. 2) система уравнений имеет вид

Получим угол наклона траектории фазовых кривых
 (5)
(5)
По формуле (5) можно сделать вывод что tg(α)=0 и tg(α)=∞ являются частными случаями движения фазовых кривых в областях с постоянными направлениями xи y.
Рассмотрим все возможные расположения этих кривых относительно фрагмента фазового пространства приведенного на рисунке 2. Для определенности предположим, что ε > 1. Все возможные расположения кривых для уравнений системы, приведены на рис. 3 при ε = 2 и β=0.
На рис. 3а приведен эллипс возможный в случае ![]() . На рис. 3б приведен случай, когда эллипс распадается на две кривые при
. На рис. 3б приведен случай, когда эллипс распадается на две кривые при ![]() . На рис. 3в приведен случай, когда две кривые распадаются на четыре при
. На рис. 3в приведен случай, когда две кривые распадаются на четыре при ![]() . На рис. 3г приведены два случая, при которых кривые отсутствуют при
. На рис. 3г приведены два случая, при которых кривые отсутствуют при ![]() и
и ![]() . Стрелками на рис. 3 показаны углы наклона фазовых траекторий.
. Стрелками на рис. 3 показаны углы наклона фазовых траекторий.
Для упрощения дальнейшего анализа заменим нелинейную функцию sin(x) переменной xв интервале ![]() , и π–x при
, и π–x при ![]() [5]. Аналогично заменяем sin(у) переменной у в интервале
[5]. Аналогично заменяем sin(у) переменной у в интервале ![]() , и π–y при
, и π–y при ![]() . Тогда уравнение (3) преобразуется к виду
. Тогда уравнение (3) преобразуется к виду
 (6)
(6)

а) | б) |

в) | г) |
Рис. 3 Фазовая плоскость с выделенными областями с постоянными направлениями x и y
На рис. 4 приведена работа ФАП в режиме захвата за сигнал при β=0, Δβ=π/2, ε=1. На рисунке приведены две фазовые кривые начинающие движение с точек a1, a2 и заканчивающие движение в точках соответственно в b1 и b2. Для режима захвата за сигнал характерно монотонное изменение координаты y. При этом координате xхарактерно следующее неравенство ![]() Соответственно для режима захвата за помеху характерно монотонное изменение координаты x, а координате yхарактерно неравенство
Соответственно для режима захвата за помеху характерно монотонное изменение координаты x, а координате yхарактерно неравенство ![]() Стрелкам на рис. 4 показаны углы наклона фазовых траекторий.
Стрелкам на рис. 4 показаны углы наклона фазовых траекторий.
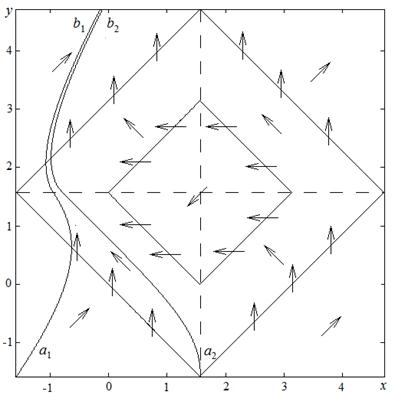
Рис. 4 Режим захвата за сигнал при ε = 1
На рис. 5 приведены фазовые плоскости с выделенными областями с постоянными направлениями x и y. Стрелками на рисунке обозначены углы наклона траектории фазовых кривых.
В случае если принять Δβ>0, то анализ фазовых траекторий можно разделить на четыре категории. В случае изображенном на рис. 5б можно заметить, что работа ФАП будет проходить в режиме захвата за сигнал. На рис. 5в работа ФАП будет проходить в режиме захвата за помеху. Рисунки 5а и 5г не дают достаточной информации о захвате за сигнал или помеху. В случае при Δβ<0 все рассуждения проводятся аналогично.
Нормируем рисунки 4 и 5, заменив шаг сетки со значения π/2 на 1. Из анализа рис. 4 и 5 становится ясно, если ![]() , в то время как
, в то время как ![]() , получим работу ФАП в режиме захвата сигнала, и при
, получим работу ФАП в режиме захвата сигнала, и при ![]() ,
, ![]() – работу ФАП в режиме захвата помехи. Подставив полученные значения x и yв систему уравнений (6), получим неравенство для ФАП в режиме захвата сигнала
– работу ФАП в режиме захвата помехи. Подставив полученные значения x и yв систему уравнений (6), получим неравенство для ФАП в режиме захвата сигнала
![]() (7)
(7)
и в режиме захвата помехи
![]() (8)
(8)

а) | б) |

в) | г) |
Рис. 5. Анализ фазовых траекторий при различных значениях ε, β
Заменив в уравнении (7) и (8) ![]() на
на ![]() ,
, ![]() на
на ![]() и ε на
и ε на ![]() , придем к уравнению (14 a) и (14 b) автора [5]. Причем следует отметить, что автором была допущена ошибка, в случае захвата за помеху неверно поставлен модуль. Верность полученных уравнений (7) и (8) можно проверить по рисунку 15.6 автора [4].
, придем к уравнению (14 a) и (14 b) автора [5]. Причем следует отметить, что автором была допущена ошибка, в случае захвата за помеху неверно поставлен модуль. Верность полученных уравнений (7) и (8) можно проверить по рисунку 15.6 автора [4].
Проверим неравенства (7) и (8) по формуле (3), получив режимы захвата за сигнал и за помеху. На рис. 6а приведен режим захвата за сигнал при ε = 0.8; β = 0; Δβ = –0.4. На рис. 6б приведен режим захвата за помеху при ε = 1; β = 0.4; Δβ = 0.4.

а) | б) |
Рис. 6 – Режимы захвата сигнала и помехи
На рис. 7 показана линия границы захвата за сигнал и за помеху вычисленная при различных ε, Δβ по формуле (3) принимая при этом β=0. Кружочками на рисунке обозначены значения Δβ, для которых проводилось моделирование.

Рис. 7 – Линия границы захвата сигнала и помехи
Заключение
Таким образом, в результате проведенного анализа были получены неравенства для определения условий захвата за сигнал и за помеху зависящие от значений отношение помеха/сигнал, сигнальной расстройки по частоте и отстройки по частоте сигнала и гармонической помехи. Для проверки полученных выводов, было проведено моделирование по полученным неравенствам режимов захвата за сигнал и за помеху.
Список литературы
1. Шахтарин Б.И. Анализ систем синхронизации при наличии помех. М.: ИПРЖР, 1996. 252 с.
2. Meyr H., Ascheid G. Synchronization in digital communications . Vol.1. Phase-, Frequency-Locked Loops, and Amplitude Control. N.Y.: Wiley, 1990. 510 p.
3. Stephens D.R. Phase – locked loops -for Wireless communications. Digital, analog and implementations. 2nd ed. N.Y.: Kluwer, 2002. 421 p.
4. Шахтарин Б.И. Анализ систем синхронизации методом усреднения. М.: Радио и связь, 1999. 495 с.
5. Nakagawa M. Effects of interfering signals in phase-locked loops // Frequentz. 1978. № 32 (5). P. 146-153.
Публикации с ключевыми словами: помехоустойчивость, фазовая автоподстройка, гармоническая помеха, отношение помеха/сигнал
Публикации со словами: помехоустойчивость, фазовая автоподстройка, гармоническая помеха, отношение помеха/сигнал
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



