научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#7 июль 2004
Разработка алгоритма фильтрации
для измерительного комплекса боевого летательного аппарата
Горячев Алексей Владимирович
Физико-математический лицей № 1580
при МГТУ имени Н.Э.Баумана, 11 класс
Научный руководитель: Неусыпин Константин Авенирович,
профессор кафедры «Системы автоматического управления»,
доктор технических наук
Введение
Решение задачи управления летательным аппаратом (ЛА) предполагает определение параметров его движения. Для этого используются различные измерительные системы, в частности инерциальные навигационные системы (ИНС) и многообразные радиолокационные системы – РЛС, ДИСС и др.
ИНС имеют погрешности, нарастающие со временем функционирования ЛА. Поэтому в практических приложениях ИНС обычно объединяют с РЛС. Совместная обработка выходных сигналов ИНС и РЛС позволяет существенно повысить точность определения навигационных параметров ЛА. Совместная обработка сигналов измерительных систем предполагает применение различных алгоритмов, например алгоритмов оценивания. Наиболее распространённым алгоритмом оценивания погрешностей ИНС является фильтр Калмана. Фильтр Калмана позволяет по разности сигналов ИНС и РЛС оценить весь вектор состояния, включающий основные погрешности ИНС. А затем оценки погрешностей ИНС вычитаются из выходного сигнала ИНС, тем самым повышается точность определения навигационных параметров ЛА. Однако применение фильтра Калмана для повышения точности ИНС сопряжено с некоторыми специфическими сложностями, связанными с достоверностью априорной информации о статистических характеристиках исследуемых процессов.
Настоящая работа посвящена исследованию способа коррекции ИНС в выходном сигнале посредством фильтра Калмана.
Принцип построения навигационных систем
Успешное решение задач управления сложными техническими системами во многом определяется уровнем развития измерительной техники. Эксплуатационные характеристики динамического объекта в большой степени определяются совершенством бортового оборудования, в частности, качеством информационно-измерительных сигналов, используемых для управления объектом. Источником информационно-измерительных сигналов о местоположении, ориентации, скорости и других параметрах движения является навигационный приборный комплекс.
В данном разделе рассматриваются различные схемы построения бортовых навигационных систем, которые применяются в самолётостроении, ракетостроении и других областях техники.
Классификация навигационных систем проводится по типу чувствительных элементов, используемых в системах, иначе по принципу действия, а также по точностным характеристикам.
Наиболее широко используются навигационные системы, основанные на принципах гироскопической стабилизации.
В ракетной технике используются свободные трёхстепенные гироскопы, которые отличаются простотой конструкции, компактностью и хорошо отработаны на практике. Свободные гироскопы устанавливаются на ракетах класса земля-воздух. Существенные погрешности этого типа в достаточной степени компенсируются с помощью простейших алгоритмов коррекции [1]. Однако на современном этапе развития ракетной техники возникает необходимость компенсировать такие погрешности свободных гироскопов, как динамический дрейф, обусловленный действием перекрёстных угловых скоростей в условиях сложного движения ЛА.
Информация об угловой ориентации ЛА относительно опорной системы координат, реализуемой блоком двух свободных гироскопов, выдаётся датчиками углов, расположенных на осях подвеса гироскопов. Эта информация искажается при нарушении ортогональности между собственным кинетическим моментом свободного гироскопа и осью подвеса наружной рамки.
В процессе полёта ЛА может совершать различные манёвры, что и приводит к нарушению ортогональности внутренней и наружной рамок гироскопа. Поворот ЛА вокруг оси, совпадающей с осью подвеса наружной рамки гироскопа, приводит к рассогласованию осей ЛА и внутренней рамки, на которой расположен датчик угла. Это также приводит к искажению информации об ориентации ЛА.
Другим достаточно часто используемым типом навигационных систем, является блок датчиков угловых скоростей, основанный на двух или трёх двухстепенных гироскопах. Системы измерения угловых скоростей, построенные на трёх двухстепенных дифференцирующих гироскопах с ортогональными измерительными осями, нашли широкое применение в системах автоматического управления движением ЛА (самолётов, ракет, космических ЛА), и в особенности в системах автоматической угловой стабилизации ЛА. Серьёзным недостатком дифференцирующих гироскопов являются погрешности, зависящие от перекрёстных угловых скоростей, возникающих при сложном движении ЛА. Метод уменьшения их введением спаренных гироскопов приводит к увеличению массы системы и к появлению других погрешностей, вызванных трением в шарнирном соединении спаренника и в осях подвеса спаренных гироскопов.
Самым распространённым типом навигационных систем в настоящее время являются системы, в которых используется гиростабилизированная платформа (ГСП). На ГСП возлагаются задачи по управлению и стабилизации специальных бортовых приборов, таких как антенны бортовых радиолокационных станций, чувствительные элементы пеленгаторов, координаты цели, аэрофотоаппаратура, акселерометры и т.д. ГСП удерживает стабилизируемый объект на заданных направлениях в пространстве.
ГСП может быть построена на гироскопах различных типов: лазерных и электростатических гироскопах, динамически настраиваемых, поплавковых и других гироскопах. ГСП имеет погрешности, обусловленные типом применяемых гироскопов и конструкцией платформы. Специфические погрешности, присущие различным типам гироскопов успешно компенсируются, а динамический дрейф ГСП, достигающий в современных системах значительных величин по сравнению с остаточными (после компенсации) погрешностями, как правило, не компенсируется.
На объектах, предназначенных для осуществления длительных полётов в непосредственной близости от поверхности Земли, широкое распространение получили инерциальные навигационные системы (ИНС).
Бесплатформенные ИНС (БИНС) для получения навигационной информации относительно выбранной системы координат моделируют математический маятник с периодом Шуллера посредством информации о линейных ускорениях и угловых скоростях несущего объекта. БИНС могут включать акселерометры, которые жёстко крепятся на борту ЛА, либо перемещаются по заданному закону, или акселерометры и измерители и измерители угловых скоростей.
Достоинствами БИНС по сравнению с платформенными ИНС обычно считаются большая надёжность, простота эксплуатации и меньшая стоимость. Хотя требования к точностным характеристикам акселерометров и гироскопов более высокие, так как чувствительные элементы БИНС жёстко закреплены непосредственно на корпусе, ЛА находятся в чрезвычайно жёстких условиях эксплуатации.
ИНС и ГСП в зависимости от ориентации осей акселерометров в пространстве могут быть выполнены по геометрической, полуаналитической и аналитической кинематическим схемам.
ИНС, построенные по геометрической схеме, представляют собой платформу с акселерометрами, измерительные оси которых ориентированы в географической системе координат. Платформа поворачивается при движении несущего объекта таким образом, что всё время находится в плоскости местного горизонта, оси же гиростабилизатора остаются в угловом смысле неизменными в инерциальном пространстве. Относительно инерциального пространства и соответственно гиростабилизатора измерительные оси акселерометров поворачивают с угловой скоростью, которая равна скорости вращения Земли и относительного движения несущего объекта.
В ИНС аналитического типа материализуется в угловом смысле неподвижная в инерциальном пространстве система координат, относительно которой ведутся все отсчёты навигационных параметров динамического объекта. Требования к БЦВМ при использовании ИНС аналитического типа более высокие, чем у вышеперечисленных типов ИНС.
Наиболее распространённой является полуаналитическая схема построения ИНС. Эта схема характеризуется тем, что система координат запоминается в БЦВМ, а сопровождающий трёхгранник материализуется посредством ГСП с акселерометрами. Оси чувствительности акселерометров ориентированы относительно земной поверхности по осям ортодромической, азимутально-свободной или географической системы координат. Сохранение ГСП горизонтального положения и выбранной ориентации в азимуте достигается посредством настройки системы на период Шуллера, равный 84,4 минуты. В этом случае достигается инвариантность системы к горизонтальным ускорениям несущего объекта.
ИНС, построенные по полуаналитической схеме, могут быть реализованы на базе трёх двухстепенных гироскопов или двух трёхстепенных гироскопов. Интегрирование сигналов с акселерометров даёт информацию о скорости несущего динамического объекта. Двукратное интегрирование позволяет определить пройденный путь вдоль соответствующих осей.
Коррекция ИНС от внешних источников информации с применением различных алгоритмов позволяет существенно снизить погрешности получаемой навигационной информации. В качестве примера использования алгоритмов для коррекции навигационной информации рассмотрим ИНС с внешним источником информации, в качестве которого применяется ДИСС.
Для наиболее полной компенсации погрешностей в выходной информации необходимо предварительно оценить ошибки ИНС. Учитывая, что ДИСС измеряет только скорости, нужно по имеющейся информации об ошибках по скорости оценить ошибки по углу и дрейф гироскопов. Оценить ошибки в измерении этих параметров возможно, воспользовавшись алгоритмами оптимального оценивания. Алгоритм оценивания вычисляет все оценки ошибок ИНС, поддающиеся наблюдению.
Входным сигналом для алгоритма оценивания является разность в измерении скорости с помощью ИНС и ДИССа. Ошибки ИНС составляют вектор состояния системы и включают ошибки по скорости, по углу и дрейф гироскопов, а ошибки ДИССа представляют собой измерительный шум.
После обработки измерений на выходе алгоритма оценивания получаем оценку вектора состояния, т.е. оценку всех наблюдаемых ошибок ИНС.
Далее оценка ошибок ИНС алгебраически вычитается из выходного сигнала ИНС, состоящего из достоверной информации о скорости и местоположении объекта и ошибок ИНС. Тем самым компенсируются в выходном сигнале ошибки ИНС в определении навигационных параметров.
Оценку ошибок ИНС можно использовать в регуляторе для компенсации ошибок по скорости, по углу и дрейфу гироскопов в структуре ИНС, уменьшая тем самым амплитуду колебаний ошибок и улучшая качество переходного процесса.
Схема подключения к ИНС алгоритма оценивания (АО) представлена на рис. 1.
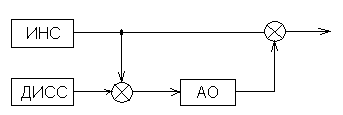
Рис. 1. Схема подключения к ИНС алгоритма оценивания
Применение схемы (рис. 1) предполагает использование нерасходящихся высокоточных алгоритмов оценивания и управления, требующих малого объёма машинной памяти, которые легко могут быть реализованы на БЦВМ.
Алгоритм оценивания
Наиболее распространённые методы компенсации погрешностей навигационных систем предполагают использование различных алгоритмов оценивания.
Учитывая специфику реализации алгоритмического обеспечения на борту динамического объекта в условиях дефицита объёма машинной памяти, выделим среди многообразия алгоритмов оценивания лишь компактные и робастные алгоритмы.
Достаточно высокой точностью и в то же время простотой реализации в БЦВМ отличаются адаптивные алгоритмы оценивания, являющиеся прямыми модификациями фильтра Калмана [1, 2].
Рассмотрим дискретное линейное уравнение, описывающее динамический объект, например, изменение погрешностей ИНС.
xk+1 = Фk+1, kxk + Gk+1, kWk , (1)
где xk – n-вектор состояния; Wk – r-вектор входного возмущения;
Фk+1, k – (nxn)-матрица объекта; Gk+1, k – (nxr)-матрица входа.
Входные возмущения предполагаются r-мерным дискретным аналогом гауссового белого шума с нулевым математическим ожиданием и известной ковариационной матрицей:
M[wj wTk ] = Qkdj, k ,
где Qk – неотрицательно определённая матрица размерности (rxr);
dj, k – символ Кронекера, означающий
![]() 1, если j = k ,
1, если j = k ,
dj, k =
0, если j ≠ k
Часть вектора состояния измеряется:
zk+1 = Hk+1xk+1 + Vk+1 (2)
Здесь zk+1 – m-вектор измерений; Vk+1 – m-вектор ошибок измерения;
Hk+1, k – (mxn)-матрица измерений.
Ошибки измерений предполагаются m-мерным дискретным аналогом гауссового белого шума, для которого M[Vk+1] = 0,
M[Vj VTk+1] = Rk+1 dj, k+1;
где Rk+1 – неотрицательно определённая матрица размерности (mxm).
Ошибки измерения (иначе измерительный шум) и входные возмущения (иначе входной шум) некоррелированы:
M[VjWTk] = 0 при любых j и k.
Начальное значение вектора состояния полагаем гауссовым случайным вектором с нулевым математическим ожиданием, независящим от входных возмущений ошибок измерений: M[x0WTk] = 0;
M[x0VTk+1] = 0 для любого k.
Ковариационная матрица M[x0xT0] = P0 представляет собой неотрицательно определённую матрицу размерности (nxn).
На основе математического ожидания объекта и априорной информации о статистических характеристиках входных и измерительных шумов и, осуществляя измерения части вектора состояния, требуется оценить вектор состояния так, чтобы функционал J принимал минимальное значение.
Jk = M[(xk – ![]() k)T(xk –
k)T(xk – ![]() k)] = min.
k)] = min.
Здесь xk – оценка вектора состояния.
Оптимальная оценка вектора состояния определяется из уравнения вида [2]:
![]() k+1 = Фk+1, k
k+1 = Фk+1, k![]() k
+ Kk+1vk+1
(3)
k
+ Kk+1vk+1
(3)
где Kk+1 – (nxm)-матрица усиления фильтра,
vk+1 = zk+1 – Hk+1, kФk+1, k![]() k
– обновляемая последовательность.
k
– обновляемая последовательность.
Уравнение (3) имеет следующий физический смысл. На основе оценки вектора состояния и матрицы объекта производится прогноз для следующего шага вычисления оценки. Одновременно производится коррекция этого прогноза посредством использования обновляемой последовательности. Обновляемая последовательность представляет собой сумму ошибки прогноза и измерительного шума.
Матрица усиления фильтра определяет вес, с которым входит обновляемая последовательность в оценку вектора состояния. В случае проведения идеальных измерений, т.е. когда измерительный шум отсутствует, матрица усиления выбирается максимальной. Чем больше измерительный шум, тем с меньшим весом учитывается обновляемая последовательность при формировании оценки вектора состояния.
Фильтр Калмана имеет вид:
![]() k+1 = Фk+1, k
k+1 = Фk+1, k![]() k
+ Kk+1vk+1
k
+ Kk+1vk+1
P(k+1)/k = Фk+1, kPkФTk+1, k + Qk
(4)
K k+1 = P(k+1)/kHT k+1[H k+1P(k+1)/kH T k+1 + R k+1]-1
P k+1 = (I - K k+1H k+1)P(k+1)/k
Здесь P(k+1)/k – априорная ковариационная матрица ошибок оценивания;
P k+1 – апостериорная ковариационная матрица ошибок оценивания.
При помощи фильтра Калмана осуществляется не только восстановление всего вектора состояния системы, но и подавляется влияние измерительного шума.
Скалярные алгоритмы оценивания
Традиционные методы оценивания предполагают использование полной математической модели исследуемого процесса. Это обстоятельство затрудняет реализацию традиционных алгоритмов оценивания на борту объекта в условиях дефицита машинной памяти. Скалярный подход [1] позволяет существенно уменьшить объём машинной памяти, необходимый для организации процедуры оценивания, а также сократить время счёта. Скалярные алгоритмы представляют собой формулы с переменными коэффициентами, позволяющие проводить оценивание отдельно каждой компоненты вектора состояния. Для синтеза скалярных алгоритмов оценивания необходимо сформировать скалярное уравнение модели для интересующей компоненты вектора состояния и приведённые измерения.
![]() ink+1
= bii
ink+1
= bii![]() in(k-1)+1
+ kik(zi*k+1 – biixin(k-1)+1
– yik) + yik
in(k-1)+1
+ kik(zi*k+1 – biixin(k-1)+1
– yik) + yik
yik = biiz2*k + bi2z2*k + … + binzn*k
(5)
kik = Pik/(k-1)/( Pik/(k-1) + rik)
Pik/(k-1) = b2ii(1 - kik-1) Pi(k-1)/(k-2) + q ik-1
Pik/(k-1) – априорная дисперсия ошибки оценивания;
qik-1 – дисперсия входного шума, приведённого к i-ой компоненте вектора состояния;
rik – дисперсия измерительного шума, приведенная к i-ой компоненте вектора состояния.
Результаты математического моделирования
Для проверки работоспособности алгоритмов оценивания использована математическая модель погрешностей ИНС [1].
xk = Фxk-1 + Wk-1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() dV
1 –gT 0
B
dV
1 –gT 0
B
где xk = j Ф = T/R 1 T Wk-1 = 0
e 0 0 1 wk-1
B - смещение нуля акселерометра, B = 10-2,
wk-1 – дискретный аналог белого гауссового шума [1].
Предположим, что измеряется только первая компонента вектора состояния, т.е.
zk = Hxk + Vk ,
где zk – вектор измерений.
H = [ 1 0 0 ]
Vk – измерительный шум, который представляет собой дискретный аналог белого гауссового шума;
Wk-1 и Vk – независимые процессы.
Результаты моделирования погрешностей ИНС представлены на рис. 2–4.
Фильтр Калмана оценивает весь вектор состояния и подавляет измерительный шум. Оценка будет оптимальной, если правильно выбраны априорные значения матриц Q и R. Рис. 2. sdV = 6.6863 м/мин.
В оптимальном случае
![]()
![]()
![]()
![]() 10-4 0 0
10-4 0 0
Q = 0 0 0 , R = 2500.
0 0 10-10
Однако оптимальный выбор Q и R возможен только в случае, когда характеристики процессов W и V известны точно.
На практике такие случаи встречаются крайне редко [1]. Поэтому продемонстрируем качество оценивания фильтром Калмана процессов с неизвестными характеристиками входного и измерительного шумов.
Пусть Q завышено на порядок
![]()
![]()
![]()
![]() 10-3
0 0
10-3
0 0
Q = 0 0 0
0 0 10-9 .
Тогда среднеквадратическое отклонение получаем:
sdV = 7.6866 м/мин.
Результаты моделирования представлены на рис. 3.
Если принято заниженное на порядок значение Q, то оценка получается несколько лучше. См. рис. 4.
Среднеквадратическое отклонение будет в этом случае следующим:
sdV = 7.4252 м/мин.
Теперь будем изменять матрицу R. При R = 250 результаты моделирования представлены на рис. 5.
Среднеквадратическое отклонение
sdV = 5.2003 м/мин.
При R = 25000 – соответственно рис. 6.
Среднеквадратическое отклонение
sdV = 15.1166 м/мин.
Таким образом, можно сделать вывод о том, что неточное задание матрицы Q оказывает большее влияние на точность оценивания, чем неопределённость информации об R.
В случае оценивания Фильтром Калмана погрешностей ИНС необходимо использовать адаптивные модификации фильтра Калмана. По крайней мере, адаптивным образом определить матрицу Q.

Рис.2

Рис.3

Рис.4
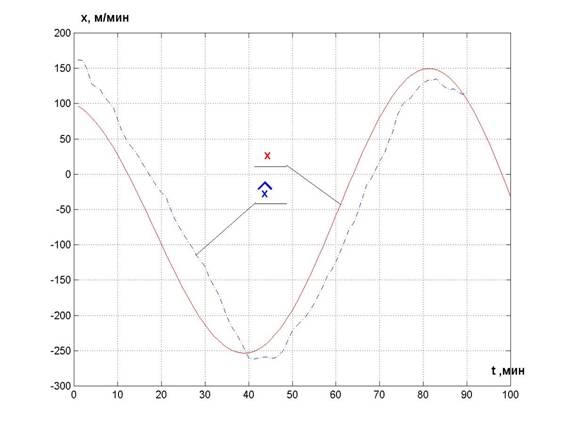
Рис.5

Рис.6
Заключение
В настоящей работе представлен алгоритмический метод повышения точности ИНС посредством компенсации погрешностей в выходном сигнале системы. Для определения оценок погрешностей ИНС использован фильтр Калмана. Проведено исследование особенностей функционирования фильтра Калмана при различных априорных данных.
Результаты математического моделирования показали, что в условиях отсутствия достоверных априорных данных о характеристиках шумов использовать фильтр Калмана нецелесообразно, т.к. ошибки оценивания слишком велики и не позволяют повысить точность ИНС. Коррекцию ИНС посредством фильтра Калмана возможно проводить только при условии, что характеристики шумов могут быть определены с достаточно высокой точностью. В этом случае с помощью фильтра Калмана получается оптимальная оценка погрешностей ИНС и удаётся существенно повысить точность определения навигационных параметров ЛА.
Список литературы:
1. Пупков К.А., Неусыпин К.А. Вопросы теории и реализации систем управления и навигации.– М.: Биоинформ, 1998.– 368 с.
2. Кузовков Н.Т., Салычев О.С. Инерциальная навигация и оптимальная фильтрация.– М.: Машиностроение, 1978.– 215 с.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



