научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#5 май 2004
А.Н. Божко, А.Ч. Толпаров
Структурный синтез на элементах с ограниченной сочетаемостью
Введение
Теорию автоматизированного проектирования принято считать сравнительно молодой наукой, но если вести ее хронологию с первых публикаций, датированных пятидесятыми годами прошлого столетия, то оказывается, что эта дисциплина скоро будет справлять полувековой юбилей. Многими специалистами по CAD-системам [7,16] отмечается несколько однобокое развитие этой технической науки. Большая часть работ по теории проектирования посвящена вопросам параметрического синтеза и геометрического моделирования технических систем. Структурному синтезу уделяется внимание, совершенно не сопоставимое с удельным весом и важностью этой задачи в общем цикле проектных работ по разработке машин и приборов [8, 14].
Качество результатов генерации проектных решений связано, прежде всего, с уровнем средств математического обеспечения САПР. В этом отношении пути внедрения в САПР методов формального синтеза и моделирования оказались различными. Автоматизированный параметрический синтез нашел адекватное представление в терминах традиционного математического аппарата, опирающегося на глубоко разработанные методы математического анализа и теории дифференциальных уравнений. Мощную математическую поддержку получили проблемы автоматизированного геометрического моделирования, поставленные перед разработчиками первых CAD-систем. Математическое обеспечение задач автоматизированного геометрического моделирования было заимствовано из одной из наиболее глубоких и проработанных отраслей математики — геометрии. Структурное проектирование, особое значение которого определяется тем, что именно структура объекта несет в себе основную информацию о функциональном назначении объекта и определяет его основные технические характеристики, адекватного формального описания не получило до настоящего времени.
Задача структурного синтеза, в своих многочисленных постановках, привлекает к себе внимание специалистов различного профиля. Совокупность исследований по этой проблематике можно в разбить на два ведущих направления.
В первом задача структурного синтеза решается на предметном уровне, не выходя за рамки конкретного типа, в редких случаях класса, технических объектов. Основной массив работ в этой парадигме выполнен специалистами-схемотехниками в области цифровой, вычислительной техники и информационных систем [8,9].
Второе направление, возникшее сравнительно недавно, ставит своей целью разработку универсальных методов структурного синтеза, применимых для различных технических объектов и независящих от отраслевой или цеховой специфики [11]. Полигоном для отработки идей и проверки полученных результатов служит область теории проектирования, связанная с синтезом физических эффектов и технических принципов действия.
Синтез представляет собой проектную процедуру, целью которой является соединение различных элементов, свойств, сторон и т. п. объекта в единое целое, систему. В результате синтеза создаются проектные решения, обладающие новым качеством относительно своих элементов.
Объем понятия синтез в технике очень велик [3,10,11,13]. Так, в качестве синтезируемых проектных решений могут выступать: машины, приборы, алгоритмы, установки, технологические и вычислительные процессы, структуры технических систем, физические принципы действия, отдельные технические решения, алгоритмы, программы и т. д.
Классификация задач синтеза
Существует много классификаций задач синтеза. Так, в качестве классификационного признака могут быть выбраны уровни, стадии, этапы, аспекты процесса проектирования, виды синтезируемых проектных решений, характеристики математических моделей, сложность и трудоемкость решения задачи синтеза, способы решения и многое другое. Современное состояние исследований в области автоматизированного синтеза не дает оснований для построения достаточно полной и непротиворечивой классификации задач синтеза. Поэтому, классификация, представленная на следующем рисунке, не является окончательной; ее можно рассматривать лишь как правдоподобную гипотезу о возможном представлении задач синтеза.

рис. 1. Классификация задач синтеза
Для того чтобы синтезировать объект, необходимо определить его структуру, параметры элементов, а если объект представляет собой техническую систему, то и конструкцию. Эти три части задачи синтеза называются соответственно структурным, параметрическим синтезом и синтезом конструкции.
Параметрический синтез заключается в определении значений параметров элементов при заданной структуре и условиях работоспособности. Если воспользоваться геометрическими аналогиями, то задачу параметрического синтеза можно сформулировать как задачу поиска в N-мерном пространстве внутренних параметров такой точки (набора из N значений параметров), для которой либо просто выполняются условия работоспособности, либо выполняются наилучшим образом. В первом случае требуется, чтобы решение задачи параметрического синтеза принадлежало некоторой замкнутой и ограниченной области пространства внутренних параметров, для каждой точки которого выполняются условия работоспособности. Во втором случае решение представляет собой точку пространства, наилучшую согласно принципу оптимальности, который формализует понятие наилучшего выполнения условий работоспособности. Если разработана математическая модель объекта, то по постановке и методам решения, задача_параметрического синтеза в первом случае сводится, а во втором случае является задачей оптимизации.
Синтез конструкции связан с проектированием геометрического облика изделия. Это сложная, трудноформализуемая задача. Методы решения таких задач основаны на использовании развитых графических сред, работающих в режиме диалога между проектировщиком и компьютером.
Структурный синтез
Понятие структуры нашло широкое применение в естественнонаучных и технических дисциплинах. Например, можно говорить о структуре системы, процесса, машины или прибора, алгоритма и программы, образа и ситуации. Развиваются и имеют плодотворные приложения структурные методы исследования в лингвистике, распознавании образов, теории автоматического управления, кибернетике.
Существует большое количество определений структуры. Например, структурой называют способ организации целого из частей или, даже, меру неоднородности окружающей среды [3,18]. Под структурой объекта (технической системы, процесса) будем понимать совокупность составляющих его элементов и связей между ними.
Сфера приложений понятий структура и структурный синтез в технике очень велика. Можно утверждать, что все проектные решения структурны. Например, физический принцип действия устройства состоит из отдельных физических эффектов; любая техническая система состоит из подсистем и элементов; элементами технологического, вычислительного и других процессов являются операции; структуру алгоритма образуют блоки псевдокода; программа состоит из операторов и т. д.
В результате решения задачи структурного синтеза должно быть получено описание состава изделия и всех существенных связей между его ‘элементами. В зависимости от вида проектного решения таким описанием может быть простой перечень элементов и связей между ними, таблица соединений, матрица инцидентности, граф связей, структурная схема, блок-схема, эскиз, компоновка чертеж и пр.
Несмотря на существенные различия существующих технических систем и процессов для всех них можно предложить общую постановку задачи синтеза. А именно, задана функция (функциональное назначение, закон функционирования), требуется разработать описание объекта (технической системы, процесса), который реализует заданную функцию и удовлетворяет некоторой совокупности ограничений и особых условий.
Понятие функции технической системы широко используется в методиках поискового конструирования, функционально-стоимостного анализа, в патентоведении и других сферах инженерной деятельности [7,11,14,15]. Однако не существует общепринятого определения функции, функционального назначения. Под функцией технической системы будем понимать закон преобразования заданных входных величин в требуемые выходные величины, т. е. зависимость выходов объекта от его входов.
Это определение предполагает, что синтезируемый объект представляется в виде «черного ящика». Его входами являются любые существенные воздействия среды (надсистемы) на синтезируемый объект, выходами—связи объекта со средой. Отношение вход-выход, развернутое во времени, представляет собой закон функционирования (функцию) синтезируемого объекта.
Концепция «черного ящика» не накладывает никаких ограничений на природу и свойства входов, выходов и отношений между ними. Таковыми могут быть материальные, энергетические, информационные, детерминированные, стохастические, генетические и т. п. связи. В общем случае отношение между входами и выходами синтезируемого объекта можно рассматривать как связь между возможными причинами и необходимыми следствиями.
На возможные реализации синтезируемого объекта накладываются ограничения. Они могут иметь различный технический, физический, технологический, гуманитарный и др. характер. Например, могут лимитироваться масса, габаритные размеры, исполнительные размеры, элементный состав, возможные структуры и т. п. синтезируемого объекта. Существуют ограничения, связанные с наличием прототипов, аналогов, с патентной чистотой варианта. Особые условия и ограничения позволяют более четко определить класс, к которому принадлежит синтезируемый объект.
Приведем примеры задач синтеза. Пусть необходимо синтезировать технологический процесс изготовления некоторой детали. На этапе постановки задачи синтеза сам технологический процесс представляется в виде «черного ящика», входами которого служат характеристики заготовки (конфигурация, марка материала, шероховатость поверхностей и пр.), выходами характеристики готовой детали (геометрия обработанных поверхностей, их взаимное расположение, точность, шероховатость и т. п.). В качестве ограничений выступают такие свойства производственной и технологической систем, как совокупность видов обработки, состав технологического оборудования, типовые маршруты и операции и т. п.
Пусть требуется разработать редуктор по заданным входным моменту и угловой скорости и выходным моменту и угловой скорости. В этой задаче синтеза входами и выходами («черного ящика» — редуктора) являются моменты и угловые скорости. В зависимости от проектной ситуации ограничениями могут быть требования к количеству ступеней редуктора, к виду зацеплений, расположению осей, габаритным размерам, массе и т. п.
При синтезе алгоритма упорядочения входом алгоритма, представленного в виде «черного ящика», является множество элементов любой природы, каждому из которых поставлено в соответствие некоторое число—ключ. Выходом алгоритма служит множество, отсортированное по увеличению (уменьшению) ключа. Особые условия и ограничения могут требовать, например, чтобы алгоритм упорядочения сохранял работоспособность в тех случаях, когда областью определения ключа являются натуральные, целые, действительные числа.
Задача структурного синтеза проектных решений, с точки зрения возможности формализации, относится к числу наиболее сложных. Это связано с тем, что с одной стороны, свойства синтезируемого объекта зависит от большого числа зачастую случайных, противоречивых, но не до конца исследованных, факторов. Эта причина имеет объективный характер. С другой стороны, при решении задачи синтеза часто приходится выбирать вариант из множества очень большой конечной или даже счетной мощности. При проектировании функциональных схем блоков радиоэлектронной аппаратуры существует бесчисленное множество вариантов, различающихся количеством элементов, типами элементов, способами их взаимосвязи. Кроме того, если задача синтеза поставлена в терминах некоторой формальной системы, то для реализации такого выбора необходимо решить задачу очень высокой размерности. Например, решить задачу дискретной оптимизации на множестве, состоящем из большого числа элементов. При этом могут потребоваться такие вычислительные мощности, которые превосходят возможности современных компьютеров.
Большая размерность задач синтеза технических объектов делает целесообразным применение блочно-иерархического подхода, при котором весь процесс синтеза объекта разбивается на совокупность взаимосвязанных иерархических уровней. Это значит, что синтезируется не весь объект в целом, а на каждом иерархическом уровне синтезируются определенные подсистемы, уровень детализации которых соответствует принятому способу декомпозиции системы на подсистемы. Такой подход существенно упрощает решение задачи синтеза.
Традиционно процесс проектирования делится на стадии предварительного, технического и рабочего проектирования. Можно говорить о процессе синтеза, который состоит из последовательности процедур, упорядоченных согласно декомпозиции процесса проектирования на стадии. Эта упорядоченность процедур синтеза такова [16].
На стадии предварительного проектирования синтезируются основные, принципиальные решения, определяющие концепцию технического объекта. Такими решениями могут быть: физический принцип действия устройства, облик летательного аппарата, архитектура вычислительной системы и т. п.
На стадии технического проектирования синтезируются проектные решения, уточняющие и реализующие концепцию технического объекта. Например, разрабатываются конструктивные реализации физических эффектов, образующих физический принцип действия устройства. На стадии рабочего проектирования синтезируются все параметры и разрабатывается конструкторская документация на объект.
Комбинаторно-логические методы структурного синтеза
Среди всех подходов к решению задачи структурного синтеза наибольшее распространение в системах автоматизированного проектирование получили различные методы, принадлежащие к классу комбинаторно-логических. В основе этого подхода лежит хорошо организованные перебор в массиве решений, которые являются аналогами и прототипами.
Рассмотрим основные допущения:
· Проектируемый объект, будь то техническая система или процесс, имеет структуру;
· Проектируемый объект принадлежит к некоторому классу объектов (множество аналогов и прототипов), имеющих одинаковое функциональное назначение.
· Множество аналогов и прототипов обладает достаточной мощностью, для того, чтобы поиск новых сочетаний в этом комбинаторном пространстве был результативен;
· Составные части объектов класса обладают «хорошими комбинаторными способностями». Это значит, что принципы действия объектов не различаются настолько, чтобы запретить объединение разных компонент в составе нового объекта.
Структуру класса объектов, имеющих одинаковое функциональное назначение, принято называть обобщенной. Элементы этого класса являются аналогами и прототипами реализуемого проекта. Обобщенная структура представляет собой "комбинаторное пространство", в котором находятся различные сочетания элементов, образующие структуры разрабатываемого технического объекта. В качестве средств описания обобщенных структур используются табличные, алгебраические, логические и сетевые модели. Классификация методов комбинаторно-логического синтеза показана на следующем рисунке.
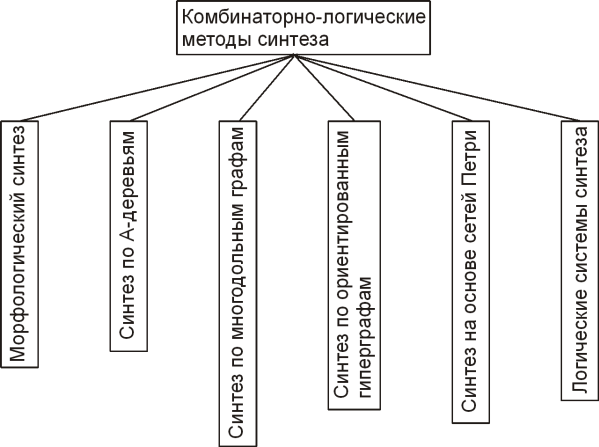
рис. 2. Классификация методов комбинаторно-логического синтеза
Наибольшее распространение среди этих моделей получили морфологические таблицы и А-деревья (И—ИЛИ-деревья — в исследованиях по искусственному интеллекту и в программировании).
Морфологические таблицы применяются на ранних стадиях проектирования и конструирования: при решении изобретательских задач, для обликового проектирования некоторых технических объектов и т. п. Таблицы позволяют получать составы (структуры без связей), структуры с линейными связями и регулярные структуры, причем все решения состоят из равного количества элементов.
Под обобщенной структурой будем понимать структуру класса объектов, имеющих одинаковое функциональное назначение. Обобщенная структура составляется на основе знаний данной предметной области, обобщения инженерного опыта и традиций, анализа аналогов и прототипов. Она содержит информацию об альтернативных вариантах устройства объектов данного класса. Например, если четко ограничить тактико-технические характеристики летальных аппаратов, то множество проектов данной направленности образует класс, который на структурном уровне описания можно рассматривать как обобщенную структуру.
Со времени изобретения бумаги в древнем Китае было предложено множество технических решений для письма. Этот класс объединяет громадное количество самых разнообразных проектов: от кисточек, которыми пользовались авторы изобретения, до автоматических многоцветных ручек современной фабрикации. Любое устройство, предназначенное для письма на бумаге, не отличается рекордной технической сложностью, но даже самые простые технические решения обладают структурой, и их совокупность — обобщенной структурой.
Существует несколько модификаций метода синтеза на основе обобщенной структуры. Они отличаются друг от друга способом описания обобщенной структуры, методами поиска решений, средствами описания запрещений на сочетание различных альтернатив и т. д. Рассмотрим некоторые разновидности метода синтеза на основе обобщенной структуры, получившие наибольшее распространение в практике проектирования.
Метод морфологического синтеза
Этот метод предложен швейцарским астрономом и инженером Ф. Цвикки. В работах автора и во многих других источниках, где акценты с проблемы синтеза новых решений смещены на составление обобщенной структуры, метод описан под названием метода морфологического анализа.
Метод морфологического синтеза применяется на ранних стадиях проектирования и конструирования; он позволяет найти и систематизировать все возможные способы построения объекта, имеющие данное функциональное назначение (9, 13). Средством, описывающим обобщенную структуру класса, служит так называемая морфологическая таблица (морфологический ящик) (рис. 3). Это простой объект с хорошо отработанными правилами заполнения и поиска решений. Техника работы с морфологическими таблицами подробно рассматривается в [6,7,11,15,17], поэтому не будем останавливаться на ней. Приведем лишь пример, иллюстрирующий основные идеи этого метода. На следующем рисунке показан небольшой фрагмент морфологической таблицы, описывающей возможные технические реализации точечной сварки.

рис. 3. Пример морфологической таблицы
Любую морфологическую таблицу можно задать в виде матрицы инцидентности. Матрица инцидентности представляет собой прямоугольную (0,1)-матрицу A=||aij|| размера L*E, где L—число морфологических классов; Е — число элементов системы (реализация). Элемент матрицы aij, стоящий на пересечении i-jй строки и j-го столбца равен единице, если реализация j входит в морфологический класс с номером I, нулю — в противном случае.
Для того чтобы по матрице инцидентности А синтезировать вариант системы, необходимо выбрать совокупность из L (по числу морфологических классов) элементов матрицы, для которой выполняются условия:
· все элементы матрицы инцидентности, принадлежащие совокупности, равны единице;
· никакие два элемента не лежат на одной линии матрицы (линией матрицы называется ее строка либо столбец);
· выбранные элементы покрывают все строки матрицы инцидентности. (Элемент матрицы покрывает линию, если он лежит на ней).
Число элементов в совокупности равняется числу строк матрицы инцидентности. Если все элементы совокупности упорядочить по возрастанию номеров строк, которые покрываются этими элементами, и вместо каждого элемента записать номер столбца, который ими покрывается, то получится L-вектор. Этот вектор представляет собой трансверсаль семейства (a(1), a(2), ..., a(L)), где все a(i) представляют собой морфологические классы.
На ранних этапах проектирование для описания обобщенных структур часто используется математический аппарат многодольных графов (N-дольных). Это граф вида G=(X1,X2,…Xn, R), где X=UXi — множество вершин, а R множество ребер. Подмножество Xi принято называть долями графа, ребра графа могут соединять только вершины разных долей. Вершины, принадлежащие одной доле всегда являются независимым подмножеством.
При описании обобщенных структур систем и процессов элементы N-дольных графов получают следующее толкование:
· доли представляют основные технические подфункции класса;
· вершины каждой доли соответствуют техническим реализациям.
Такая интерпретация делает этот аппарат очень близким морфологическим таблицам по способу решения задачи структурного синтеза и по возможностям описания структурных связей между объектами. Далее этот аппарат будет рассмотрен более подробно.

рис. 4. Представление обобщенной структуры в виде N-дольного графа
Структурный синтез по альтернативным деревьям
Язык A-деревьев обладает большими выразительными возможностями по сравнению с рассмотренными средствами представления обобщенных структур [4,7,18].
Альтернативным деревом (A-деревом) называется вектор (G, S, γ), в котором: G=G(X, D) — корневое ориентированное дерево со множеством вершин X={xi} и множеством дуг D={dj}; S={Sk}—множество названий (номеров) связок; отображение γ: S→2D ставит в соответствие каждому имени связки s, принадлежащей S, подмножество дуг γ(s) из множества D, причем все дуги одной связки имеют общую начальную вершину.
Объекты этого типа нашли широкое применение в программировании и в исследованиях по искусственному интеллекту. В этих отраслях знаний их принято называть И—ИЛИ-деревьями.
Рассмотрим правила соответствия между элементами деревьев и обобщенными структурами.
· Корень дерева соответствует основной технической функции класса объектов.
· Висячие вершины (листья) представляют технические реализации.
· Связки дерева описывают способы разбиения технических функций на подфункции.
На следующем рисунке представлено альтернативное дерево, которое описывает фрагмент обобщенной структуры класса технологических процессов, предназначенных для обработки втулки.

рис. 5. Представление обобщенной структуры в виде А-дерева
Альтернативное дерево составляется для конкретного класса систем, изделий, процессов и описывает обобщенную структуру этого класса. Вершинам дерева могут соответствовать функции, системы, подсистемы, элементы, которые реализуют эти функции, а также признаки функций и систем. Если у вершины альтернативного дерева есть потомки, это означает, что объект, который вершина описывает, имеет структуру. Например, функция сводится к набору подфункций, система—к совокупности подсистем и элементов, признак является агрегированным и выражается через композицию более простых признаков. Концевые вершины (листья) альтернативного дерева соответствуют элементарным, бесструктурным в данном классе объектам: функциям, элементам, признакам.
Для того чтобы получить по A-дереву решение задачи синтеза, нужно выполнить следующую последовательность шагов.
· Выбрать одну из связок, исходящих из корневой вершины.
· Для каждого потомка корневой вершины выбрать по одной исходящей связке.
· Продолжать этот процесс до тех пор, пока каждая из полученных вершин-потомков не станет концевой вершиной в альтернативном дереве.
Подграф, который получается в результате такого процесса, называется графом решения (деревом решения, решающим графом). А концевые вершины, принадлежащие решающему графу, представляют собой решение задачи синтеза.
Можно дать точное рекурсивное определение графа решения. Обозначим через x корневую вершину альтернативного дерева G, через Xn —множество всех концевых вершин, через Gr — граф решений, связывающий x с множеством Xn.
· Если х—элемент Xn, то Gr состоит из единственной вершины х.
· Если x не принадлежит Xn, и если из х исходит связка K, направленная на вершины {x1, x2,…,xk}, причем существует граф решения, соединяющий вершины из Xn с каждой вершиной хi, i=l,k, то Gr состоит из вершины x, связки К, вершин {x1, x2,…,xk} и графов решения, идущих в Хn из каждой вершины множества {x1, x2,…,xk}.
· Если не выполнены условия 1 и 2, то графа решения, который бы связывал х с Xn, не существует.
Это определение корректно, так как в A-деревьях нет циклов, поэтому нет вершин, имеющих таких потомков, которые были бы их предками. Это гарантирует конечность и результативность описанной рекурсивной процедуры для A-деревьев.
Синтез проектных решений с учетом дополнительных условий
Все рассмотренные модели структурного синтеза являются композиционными. Это значит, что они, потенциально или актуально, описывают только разрешенные сочетания элементов, полученные по правилам композиции данной обобщенной структуры. Среди всех решений задачи синтеза, которые определяются по рассмотренным моделям, могут содержаться нежизнеспособные, нереализуемые варианты, а также решения, защищенные патентами. Легко согласиться с тем, что множество решений, которые дает обобщенная структура любого вида, является ограниченно применимым.
Число различных параметров, характеристик, аспектов, режимов и т. п., которые описывают свойства реальных объектов, чрезвычайно велико. Только ограниченное их количество может быть учтено и описано при моделировании. Любой реальный объект намного богаче и сложнее по своим свойствам и поведению, чем его самое полное математическое описание. Возможность и необходимость объединения элементов в решение зависит только не только от функциональной структуры класса технических объектов, которая успешно описывается формальными средствами дискретной математики. Во многих проектных ситуациях на выбор структур накладываются дополнительные условия и ограничения, не представленные на языке обобщенной структуры. Эти условия могут отражать как объективные связи различной физической природы (например, требования технологии, эргономики, технического дизайна и пр.), так и субъективные предпочтения экспертов.
Задача разработки моделей структурного синтеза, учитывающих дополнительную информацию о правилах объединения элементов в составе технической системы или процесса, является важной и актуальной. Рассмотрим возможные способы формализации таких условий.
Все дополнительные условия, наложенные на элементы обобщенных структур, можно разделить на две группы: бинарные и многоместные. Первые действуют на парах элементов, вторые могут регламентировать выбор подмножеств объектов любой мощности.
Анализ различных классов технических объектов показывает, что многоместные дополнительные условия композиции встречаются достаточно редко. Большая часть таких условий, имеющих прикладное значение, может быть сведена к сочетанию бинарных отношений и правил. Далее будем рассматривать только такие условия.
Можно привести множество примеров дополнительных бинарных условий из различных отраслей техники и технологии. Выбор магазинного способа хранения штифтов в автоматическом устройстве запрессовки штифтов влечет за собой включение в состав изделия шиберного узла подачи. Гайка не может присутствовать в составе прибора или машины без своей ответной части — болта, шпильки или винта. В состав бытового теплового прибора не может быть включен источник тепла, работающий на физическом принципе ядерного реактора. Самые ответственные этапы сборки машин и приборов должны заканчиваться операциями контроля. Заготовительные и прецизионные технологические операции не могут входить в один техпроцесс обработки.
Если абстрагироваться от физической природы причин, накладывающих дополнительные ограничения на выбор альтернатив, то на уровне принятия решений все объективные характеристики и субъективные соображения могут рассматриваться как условия выбора (предусловия) и последствия выбора (постусловия) структурных элементов. Приведем некоторые виды условий для гипотетических элементов x и y .
· Принуждение. Выбор x влечет выбор y;
· Необходимость. Условием выбора x служит выбор y;
· Бинарный запрет на сочетание. Элементы x и y не могут входить в одно решение;
· Двойное принуждение. Элементы x и у входят в решение одновременно.
Удобными средствами описания этих условий служат язык теории графов и аппарат математической логики.
Самым популярным видом дополнительных ограничений являются бинарные запреты на сочетания. Не будет преувеличением сказать, что этот тип отношений между парами элементов обобщенной встречается чаще всего в проектной практике инженеров различного профиля. Рассмотрим простую модель структурного синтеза, которая позволяет описать этот вид дополнительных ограничений очень лаконичными средствами без привлечения сложного комбинированного формализма.
Структурный синтез с ограничениями на основе N-дольных графов
Аппарат двудольных графов давно и плодотворно используется в дискретной математике для решения различных задач, имеющих большое теоретическое и прикладное значение. Намного менее известно расширение этого средства на многомерный случай — так называемые N-дольные графы.
N-дольным называется граф вида G=(X, R), где множество вершин X разбито на совокупность непересекающихся подмножеств X1ИX2И…ИXN, а из существования ребра r=(z,y) следует, что инцидентные ребру вершины принадлежат разным подмножествам, т.е. zОZ, yОZ, Z,Y Н X и Z№Y. Подмножества вида Xi принято называть долями графа. Из определения следует, что все доли являются независимыми множествами вершин.
Средствами N-дольных графов можно описывать обобщенные структуры с не очень сложной системой разбиения функции на подфункции. Рассмотрим класс технических объектов, главная функция которого имеет единственное разделение на подфункции. Это основное допущение метода морфологического синтеза очень часто встречается при решении изобретательских задач и на ранних этапах проектирования.
Поставим в соответствие техническим подфункциям доли многодольного графа. Технические реализации подфункций представим в виде вершин. Пару вершин свяжем ребром тогда и только тогда, когда не существует запретов на сочетание соответствующих реализаций в составе одного технического объекта или процесса.
Аппарат многодольных графов не только дает ясный способ описания обобщенных структур с простой функциональной структурой, с его помощью можно дать четкое описание решения задачи структурного синтеза, учитывающего бинарные запреты на сочетания. Любой полный N-вершинный подграф многодольного графа является решением поставленной задачи.
Приведем обоснования этого тезиса. Его необходимость следует из алгоритма поиска решений, который полностью повторяет метод генерации решений по морфологическим таблицам. Действительно, решающий граф должен быть полным, поскольку он не может содержать запрещенные пары вершин. Чтобы технический объект отвечал своему служебному назначению, он обязан выполнять все основные технические подфункции, которые представлены долями графа. Выбор любой вершины из доли обеспечивает реализацию соответствующей технической подфункции. Это значит, что количество вершин в решающем графе должно совпадать с числом долей, которое равно N.
Обоснуем достаточность. Предположим, что существует N-вершинный полный подграф, который не является корректным решением задачи структурного синтеза. Это возможно только в случае, когда существуют по крайней мере две вершины, принадлежащие одной доли графа. Это предположение противоречит полноте решающего подграфа, поскольку по определению N-дольного графа его доли являются независимыми подмножествами.
Проиллюстририруем предложенный формализм примером небольшого фрагмента очень простого класса технических устройств «Портативные электрические фонарики». Функциональная структура этого класса показана на рис. 6.

рис. 6. Функциональная структура класса «Портативный электрический фонарик»
На рис. 7 представлен многодольный граф, построенный по заданной функциональной структуре. Легко проверить, что любой полный трехвершинный подграф этого графа представляет собой возможную компоновку электрического фонарика. Все немногочисленные запреты связаны с элементом под номером 10, который не может сочетаться в одном решении с некоторыми типами конструктивного исполнения и источниками света.

рис. 7. Представление обобщенной структуры в виде многодольного графа
В приведенном формализме требование разложимости графа на несколько долей не ограничивает общность постановки задачи. Анализ показывает, что любой граф можно разложить на совокупность долей, вершины которых не связаны друг с другом. Такое представление возможно даже для самых плотных типов графов — полных графов с произвольным числом вершин. На рис. 8 такое разложение показано на примере полного четырехвершинного графа.

рис. 8. Представление полного четырехвершинного графа в многодольном виде
Это значит, что для поиска структурных решений по многодольным графам не требуется изобретать никаких специализированных алгоритмов. Для этих целей можно воспользоваться стандартными схемами, которые предложены для графов общего вида. В работах по теории графов показывается, что задача поиска полного подграфа с фиксированным числом вершин может быть решена несколькими разными способами: как напрямую, так и при помощи сведения к графовым конфигурациям другого вида. Так, хорошо изучен метод, когда исходная задача сводится к поиску независимого множества в дополнительном графе, который, в свою очередь, формулируется как задача покрытия транспонированной матрицы инцидентности [5]. В [1] рассматривается еще одна возможная схема решения данной проблемы, которая формулируется как задача об изоморфном вложении графов.
Как и большая часть интересных и практически важных проблемы дискретной математики и теории графов все перечисленные варианты решения описанной задачи являются NP-трудными. Это означает, что все известные алгоритмы нахождения полных подграфов с фиксированным числом вершин имеют экспоненциальную трудоемкость.
Принято считать, что такое заключение делает неперспективным все попытки решения подобных задач. Это слишком пессимистический взгляд, который часто не находит практического подтверждения. Приведем несколько тезисов в защиту возможности успешного решения NP-трудных задач высокой размерности.
Принадлежность задачи к этому классу означает, что в настоящее время не известен эффективный способ решения, имеющий полиномиальную сложность. Вопрос о принципиальной возможности существования быстрого алгоритма остается открытым.
Оценка трудоемкости вычислений, которую предлагает теория вычислительной сложности — это оценка по наихудшему случаю. Такой пессимистический подход вполне уместен в теоретических исследованиях, но часто оказывается не совсем оправданным во многих практических ситуациях, когда более адекватные оценки можно получить на основе усреднения или различного вида стохастики.
Отсутствие эффективного решения для задачи в общей постановке не означает, что такое решение не может быть получено для ее частных случаев или ограничений. Высокие критерии точности и строгости, которые являются обязательными для математической постановки задачи, часто удается смягчить без ущерба для реальной проектной ситуации. Например, в оптимизационной по постановке задаче можно ограничиться поиском субоптимального решения. Вариант проекта высокой, но не абсолютной точности, способен обладать высокими тактико-техническими или потребительским свойствами, достаточными для принятия решения о его производстве.
Очевидным недостатком рассмотренного аппарата является его громоздкость. Обобщенные структуры, описывающие реальные классы объектов, могут содержать несколько десятков долей и сотни вершин в каждой из них. Любые традиционные способы кодирования таких громоздких графов (матрицы смежности, инцидентности, списки смежности и пр.) будут, очевидно, не эффективными. Задача компактного представления многодольных графов высокой размерности имеет простое и эффективное решение. Достаточно вместо самого графа хранить данные о его дополнении.
Более формально, дополнением графа G=G(X,R) называется граф L(G)=L(X, D), причем ребро r=(x,y) существует в G тогда и только тогда, когда аналогичные вершины не связаны ребром d=(x,y) в графе L. Очевидно, что объединение любого графа и его дополнения дает в итоге полный граф на том же множестве вершин, который содержит n*(n-1)/2 ребер.
Поскольку сумма ребер основного графа и его дополнения — есть величина постоянная, то большое число ребер в одном образовании означает их дефицит в его дополнении. Так, для многодольного графа, приведенного на рис. 7, его дополнение (рис. 9) представляет собой намного более компактную формацию.

рис. 9. Представление дополнительного графа
Поскольку вершины одной доли всегда попарно связаны в дополнении многодольного графа, то целесообразно эту часть описания перевести в состав умолчаний и еще более упростить описание (рис. 10).
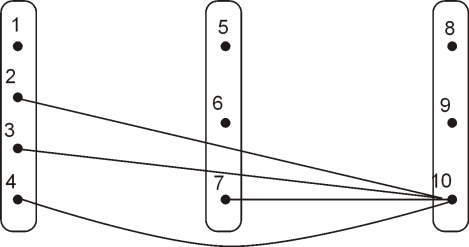
рис. 10. Редуцированное представление многодольного графа
Приведем некоторые выводы, следующие из изложенного:
· Задача структурного синтеза — это одна из важнейших задач в проектировании технических систем и процессов. Она решается для всех типов и видов объектов, независимо от их отраслевой принадлежности и выполняемых функций. К этому классу принадлежат и простейший выбор изделия из каталога стандартных решений, и сложнейшие методики синтеза, требующие усилий коллективов высококвалифицированных разработчиков. Во многих проектных ситуациях решение задачи структурного синтеза исчерпывает объем проектных работ.
· Формализации задачи структурного синтеза — это важнейшее условие создания полнофункциональных систем автоматизированного проектирования и технологической подготовки производства. Можно утверждать, что эта проблема является центральной и для теории проектирования и теории технических систем.
· Без учета дополнительных ограничений, которые накладываются на элементы и объекты трудно получить работоспособный вариант технической системы или процесса. Большинство известных подходов к решению задачи структурного синтеза не предлагают средств для описания бинарных запретов на сочетания структурных элементов. Поэтому актуальной является задача разработки такой модели структурного синтеза, которая позволяет учесть дополнительную информацию о сочетаемости объектов в составе одного решения.
· Аппарат многодольных графов позволяет описать бинарные запреты на сочетания элементов очень компактным и естественным способом. Для поиска корректных структурных решений можно применить хорошо разработанные схемы генерации полных подграфов с фиксированным числом вершин.
· Графы, описывающие реальные классы технических объектов, обладают очень высокой размерностью. Для сокращения объема описания целесообразно хранить данные о дополнении многодольного графа, которое, в общем случае, имеет намного меньше ребер, чем исходный граф.
Список литературы
2. Белоусов А.И., Ткачев С.Б. Дискретная математика М.: МГТУ, 2001
3. Глазунов В.Н. Поиск принципов действия технических систем М.: 1990
4. Голдовский, Б.И., Вайнерман М.И. Рациональное творчество М, Речной транспорт, 1990
5. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи М.: Мир, 1982
6. Дубов Ю.А. и др. Многокритериальные модели формирования и выбора вариантов систем М.: Наука, 1986
7. Евгенев Г.Б. Системология инженерных знаний. М.: МГТУ 2001.
8. Закревский А.Д. Алгоритмы синтеза дискретных автоматов М.: Наука, 1971
9. Исследования по теории структур. Сборник статей. Новосибирск.: Наука, 1986
11. Капустян В.М., Махотенко Ю.А. Конструктору о конструировании атомной техники М, Атомиздат, 1981
12. Кристофидес Н. Теория графов. Алгоритмический подход М: Мир, 1978
13. Кругликов Г.И. и др. Основы технического творчества М, Народное образование, 1995
14. Лабковский Б.А. Наука изобретать Санкт-Петербург: Нордмет, 2000
15. Мюллер И. Эвристические методы в инженерных разработках М, Радио и связь, 1984.
16. Норенков И.П. Основы автоматизированного проектирования. М.: МГТУ, 2000.
17. Одрин В.М. Картавов С.С. Морфологический анализ систем. Киев: Нукова Думка, 1977.
18. Половинкин А.И. Основы инженерного творчества М, Машиностроение, 1988
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



