научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2012
DOI: 10.7463/0812.0441895
УДК 532.591+537.84
Россия, «Московский государственный университет приборостроения и информатики»
ВВЕДЕНИЕ
В работе [1] в рамках теории магнитной жидкости с вмороженной намагниченностью впервые была показана возможность распространения быстрой и медленной магнитозвуковых волн, а так же волны альфвеновского типа. Наиболее распространенной является модель магнитной жидкости с внутренним вращением [2, 3]. В работе [4] было показано существование волны альфвеновского типа наряду со звуковой волной в модели магнитной жидкости с внутренним вращением. Для других моделей магнитной жидкости получается распространение одной гидродинамической волны [5].
1. РАСПРОСТРАНЕНИЕ ВОЛН В ФЕРРОГИДРОДИНАМИКЕ С ВНУТРЕННИМ ВРАЩЕНИЕМ
В [2, 3] предложена система уравнений для магнитной жидкости с внутренним вращением. Дисперсионное уравнение для гидродинамических волн в данной жидкости было получено и решено для двух частных случаев распространения волн параллельно и перпендикулярно внешнему магнитному полю в [4]. Целью настоящей работы является вывод дисперсионного уравнения по методу [6-8] и получение решений для всех значений угла между направлением распространения волны и внешним магнитным полем, а так же численные расчеты анизотропии скорости ультразвука.
Система уравнений для магнитной жидкости с внутренним вращением [2-4] включает в себя
уравнение непрерывности
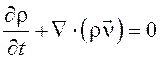 ,
,
уравнение сохранения импульса
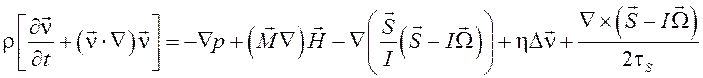 ,
,
уравнение эволюции намагниченности
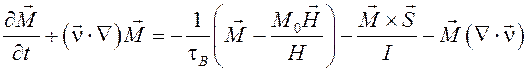 , (1)
, (1)
уравнение эволюции объёмной плотности момента импульса
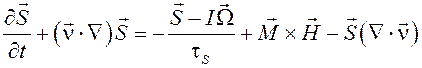 ,
,
магнитостатические уравнения Максвелла
![]() ,
,
![]() .
.
Здесь ![]() - гидродинамическая скорость магнитной жидкости;
- гидродинамическая скорость магнитной жидкости; ![]() ;
; ![]() - объёмная плотность момента импульса;
- объёмная плотность момента импульса; ![]() - плотность магнитной жидкости;
- плотность магнитной жидкости; ![]() - давление;
- давление; ![]() - момент инерции частиц, содержащихся в единице объёма магнитной жидкости;
- момент инерции частиц, содержащихся в единице объёма магнитной жидкости; ![]() - плотность твёрдой фазы;
- плотность твёрдой фазы; ![]() - объем частицы магнетита,
- объем частицы магнетита, ![]() - динамическая вязкость магнитной жидкости со сферическими твердыми частицами по формуле А. Эйнштейна (
- динамическая вязкость магнитной жидкости со сферическими твердыми частицами по формуле А. Эйнштейна (![]() - вязкость жидкости–носителя),
- вязкость жидкости–носителя), ![]() - объемная доля частиц магнетита, которая является безразмерной величиной меньше единицы;
- объемная доля частиц магнетита, которая является безразмерной величиной меньше единицы; ![]() - броуновское время ориентационной релаксации магнитного момента;
- броуновское время ориентационной релаксации магнитного момента; ![]() - время затухания собственного вращения малой частицы в вязкой жидкости,
- время затухания собственного вращения малой частицы в вязкой жидкости, ![]() - диаметр частицы магнетита.
- диаметр частицы магнетита.
Магнитные наночастицы находятся в однодоменном состоянии и слабоконцентрированная магнитная жидкость подобна суперпарамагнитному газу, поэтому равновесная намагниченность ![]() в однородном стационарном магнитном поле
в однородном стационарном магнитном поле ![]() описывается формулой Ланжевена [9]
описывается формулой Ланжевена [9]
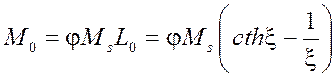 , (2)
, (2)
где ![]() ,
, ![]() - намагниченность насыщения магнетита,
- намагниченность насыщения магнетита, ![]() - константа Больцмана,
- константа Больцмана, ![]() - температура по абсолютной шкале.
- температура по абсолютной шкале.
Для исключения объемной плотности момента импульса среды ![]() в [4,10] использовано условие
в [4,10] использовано условие ![]() , поэтому из уравнения эволюции намагниченности системы (1) в линейном приближении (
, поэтому из уравнения эволюции намагниченности системы (1) в линейном приближении (![]() ,
, ![]() ) следует, что
) следует, что
![]() ,
,
где ![]() - магнитная восприимчивость.
- магнитная восприимчивость.
Линеаризованная система уравнений принимает вид [4]
 ,
,
 , (3)
, (3)
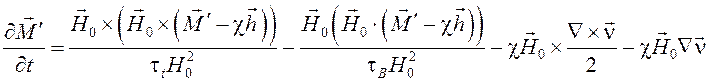 ,
,
![]() ,
,
![]() .
.
Рассмотрим распространение однородных плоских волн. Поскольку в системе (1) учитываются диссипативные процессы, то волновой вектор представлен в комплексном виде [6-8]
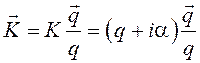
где ![]() - мнимая единица,
- мнимая единица, ![]() - волновое число и
- волновое число и ![]() - коэффициент поглощения. Считаем, что покоящаяся магнитная жидкость
- коэффициент поглощения. Считаем, что покоящаяся магнитная жидкость ![]() находится в бесконечном объёме во внешнем магнитном поле
находится в бесконечном объёме во внешнем магнитном поле ![]() , направленном вдоль оси
, направленном вдоль оси ![]() . Волновой вектор
. Волновой вектор ![]() находится в плоскости
находится в плоскости ![]() и образует угол
и образует угол ![]() с осью
с осью ![]() . Распространение волн малой амплитуды приводит к возмущению плотности, скорости и намагниченности, т. е.
. Распространение волн малой амплитуды приводит к возмущению плотности, скорости и намагниченности, т. е. ![]() ,
,![]() , и
, и ![]() .
.
Решения для возмущений переменных ![]() (штрихи пропущены) пропорциональны
(штрихи пропущены) пропорциональны ![]() , поэтому система уравнений (3) в матричной форме примет вид
, поэтому система уравнений (3) в матричной форме примет вид
![]() , (4)
, (4)
где ![]() - вектор состояния, компонентами которого являются амплитудные значения возмущений плотности
- вектор состояния, компонентами которого являются амплитудные значения возмущений плотности ![]() , скорости
, скорости ![]() и намагниченности
и намагниченности ![]() ,
, ![]() - единичная матрица.
- единичная матрица.
Ненулевые компоненты матрицы ![]() перечислены ниже:
перечислены ниже:
![]() ;
; ![]() ;
; 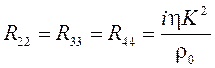 ;
; 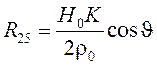 ;
;
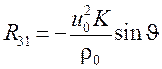 ;
; 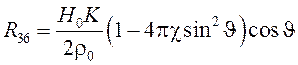 ;
;  ;
;
 ;
;  ;
;
 ;
; ![]() ;
;
![]() ;
; ![]() ;
;
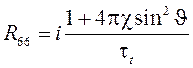 ;
; 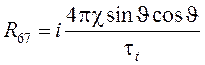 ;
;
 ;
; 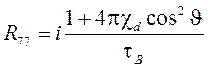 .
.
Здесь обозначено ![]() - дифференциальная магнитная восприимчивость;
- дифференциальная магнитная восприимчивость; ![]() - феноменологическое время релаксации перпендикулярной к
- феноменологическое время релаксации перпендикулярной к ![]() и
и ![]() компоненты намагниченности;
компоненты намагниченности; ![]() - скорость звука в магнитной жидкости без внешнего магнитного поля;
- скорость звука в магнитной жидкости без внешнего магнитного поля; ![]() и
и ![]() являются равновесными значениями для невозмущённого состояния.
являются равновесными значениями для невозмущённого состояния.
Приравнивая к нулю определитель матрицы (4), получаем уравнение, которое, очевидно, расцепляется на два дисперсионных уравнения
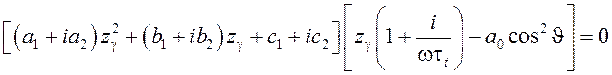 ,
,
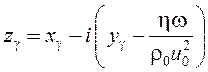 ;
; 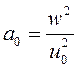 ;
; ![]() ;
;  .
.
Индекс ![]() у величин
у величин ![]() ,
, ![]() ,
, ![]() ,
, ![]() и фазовой скорости
и фазовой скорости ![]() принимает значения
принимает значения ![]() для быстрой магнитозвуковой волны,
для быстрой магнитозвуковой волны, ![]() для медленной магнитозвуковой волны и
для медленной магнитозвуковой волны и ![]() для модифицированной волны альфвеновского типа.
для модифицированной волны альфвеновского типа.
Сначала рассмотрим уравнение, которое является линейным относительно неизвестного ![]() . Данное дисперсионное уравнение описывает распространение возмущений
. Данное дисперсионное уравнение описывает распространение возмущений ![]() и
и ![]() , которые перпендикулярны волновому вектору и магнитному полю
, которые перпендикулярны волновому вектору и магнитному полю ![]() ,
,
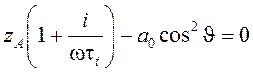 . (5)
. (5)
Выражение (5) определяет модифицированную волну альфвеновского типа [4]. Из дисперсионного уравнения (5) получаются выражения для фазовой скорости и коэффициента поглощения
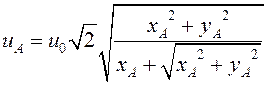 ,
,
(6)
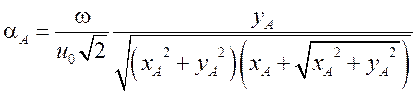 ,
,
где
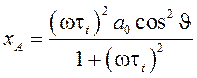 ,
,
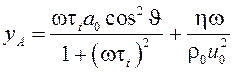 .
.
Без учета сдвиговой вязкости из (6) получаются выражения для фазовой скорости и коэффициента поглощения
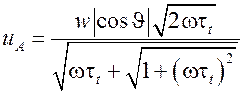 ,
,
(7)
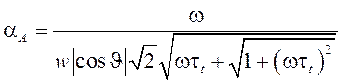 ,
,
В пределе ![]() из (7) получается волна альфвеновского типа
из (7) получается волна альфвеновского типа ![]() и
и ![]() [4], т. е. угловая зависимость получается такая же, как у волн данного типа в магнитной гидродинамике и феррогидродинамике с вмороженной намагниченностью [5]. Для
[4], т. е. угловая зависимость получается такая же, как у волн данного типа в магнитной гидродинамике и феррогидродинамике с вмороженной намагниченностью [5]. Для ![]() у
у ![]() есть расходимость, но
есть расходимость, но ![]() и волна не распространяется.
и волна не распространяется.
В случае большой вязкости модифицированная волна альфвеновского типа (6) переходит в сдвиговую волну
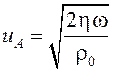 ,
,
(8)
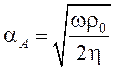 .
.
Теперь рассмотрим дисперсионное уравнение, которое является квадратным для неизвестного ![]() и описывает распространение возмущений величин
и описывает распространение возмущений величин ![]() и
и ![]() ,
,
![]() . (9)
. (9)
Коэффициенты квадратного уравнения имеют вид
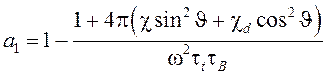 ,
,
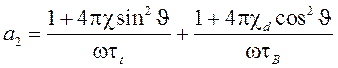 ,
,
![]() ,
,
 ,
,
![]() ,
,
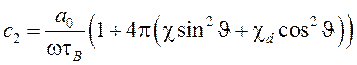 .
.
Решения уравнения (9) равны
 ,
,
где
![]() .
.
Из последних соотношений следуют выражения для фазовой скорости
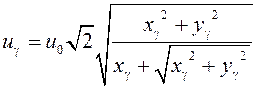 (10)
(10)
и коэффициента поглощения волн
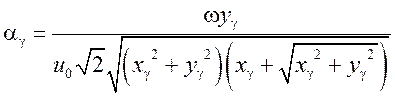 ,
,
где
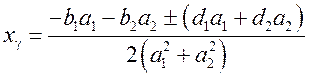 ,
,
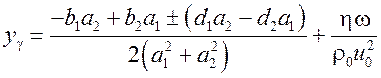 ,
,
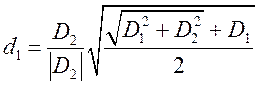 ,
,
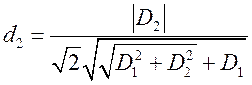 ,
,
![]() ,
,
![]() .
.
Таким образом, из дисперсионного уравнения (9) следует, что в магнитной жидкости с внутренним вращением распространяются еще два типа волн. По аналогии с магнитной гидродинамикой и феррогидродинамикой с вмороженной намагниченностью [5] назовем волну с большей фазовой скоростью быстрой магнитозвуковой волной, а с меньшей скоростью – медленной магнитозвуковой волной. Причем в выражениях для ![]() ,
, ![]() верхний знак соответствует быстрой волне, а нижний - медленной волне. Теперь отмечаем, что полученные три типа волн обладают сложной зависимостью фазовых скоростей и коэффициентов поглощения от угла
верхний знак соответствует быстрой волне, а нижний - медленной волне. Теперь отмечаем, что полученные три типа волн обладают сложной зависимостью фазовых скоростей и коэффициентов поглощения от угла ![]() , т. е. анизотропией распространения.
, т. е. анизотропией распространения.
В случае распространения волн параллельно полю, дискриминант является полным квадратом и дисперсионное уравнение (9) факторизуется в два независимых уравнения
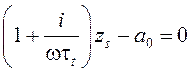 , (11)
, (11)
 . (12)
. (12)
Уравнение (11) описывает связанные осцилляции скорости и намагниченности, вектор поляризации которых перпендикулярен волновому вектору, внешнему магнитному полю и вектору поляризации модифицированной волны альфвеновского типа в данном случае. Скорость и коэффициент поглощения данной медленной волны являются такими же, как у модифицированной волны альфвеновского типа при ![]() . Можно утверждать, что параллельно магнитному полю распространяются две модифицированные волны альфвеновского типа с поляризациями по осям
. Можно утверждать, что параллельно магнитному полю распространяются две модифицированные волны альфвеновского типа с поляризациями по осям ![]() и
и ![]() .
.
Уравнение (12) определяет осцилляции скорости и намагниченности, которые параллельны волновому вектору и внешнему магнитному полю, а так же плотности.
В случае распространения волн перпендикулярно полю, дискриминант так же является полным квадратом и дисперсионное уравнение (9) преобразуется в формулу
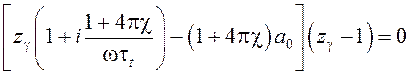 ,
,
где равно нулю произведение двух сомножителей.
Приравнивая нулю первый сомножитель, получаем дисперсионное уравнение, которое определяет медленную волну с распространением возмущений ![]() и
и ![]()
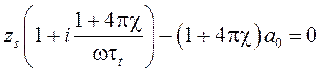 .
.
Из данного дисперсионного уравнения определяются фазовая скорость и коэффициент поглощения медленной волны
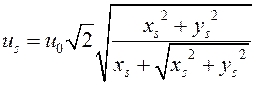 ,
,
 ,
,
где
 ,
,
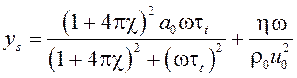 .
.
Данная медленная волна при большой вязкости переходит в сдвиговую волну (8).
В случае для малой вязкости фазовая скорость и коэффициент поглощения медленной волны имеют вид
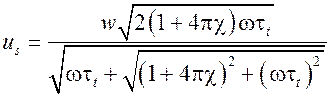 , (13)
, (13)
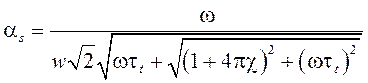 .
.
В отличие от волны альфвеновского типа медленная волна распространяется перпендикулярно внешнему магнитному полю.
Приравнивая нулю второй сомножитель получаем дисперсионное уравнение, которое определяет быструю волну с распространением возмущений ![]() ,
,![]() и
и ![]() ,
,
![]() .
.
Решениями данного уравнения являются выражения для фазовой скорости и коэффициента поглощения быстрой волны
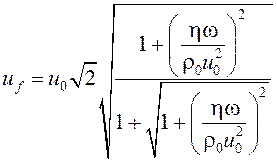 ,
,
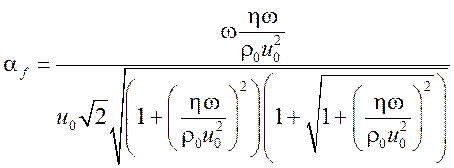 .
.
В случае малости стоксова коэффициента поглощения
![]() , (14)
, (14)
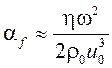 . (15)
. (15)
В пределе однородной жидкости ![]() , и поэтому
, и поэтому ![]() . В случае малости стоксова коэффициента поглощения выражения для фазовой скорости и коэффициента поглощения быстрой волны тождественны (14-15) для всех значений угла
. В случае малости стоксова коэффициента поглощения выражения для фазовой скорости и коэффициента поглощения быстрой волны тождественны (14-15) для всех значений угла ![]() . Фазовые скорости и коэффициенты поглощения медленной волны и модифицированной волны альфвеновского типа получаются как у сдвиговой волны (8) для всех значений угла
. Фазовые скорости и коэффициенты поглощения медленной волны и модифицированной волны альфвеновского типа получаются как у сдвиговой волны (8) для всех значений угла ![]() .
.
2. ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
Для численных расчетов использовались экспериментальные данные по анизотропии скорости ультразвука в магнитной жидкости EMG-605 при действии однородного стационарного магнитного поля ![]() кА/м [11]. Данная магнитная жидкость на основе воды с объемной концентрацией частиц магнетита
кА/м [11]. Данная магнитная жидкость на основе воды с объемной концентрацией частиц магнетита ![]() и плотностью
и плотностью ![]() г/см3 производится компанией Ferrotec. Inc. Номинальный диаметр частиц равняется
г/см3 производится компанией Ferrotec. Inc. Номинальный диаметр частиц равняется ![]() нм. Измерения анизотропии скорости ультразвука в [11] выполнялись при фиксированной температуре
нм. Измерения анизотропии скорости ультразвука в [11] выполнялись при фиксированной температуре ![]() . Частота ультразвука была равной 4,37 МГц. В эксперименте [11] угол
. Частота ультразвука была равной 4,37 МГц. В эксперименте [11] угол ![]() варьировался в диапазоне
варьировался в диапазоне ![]() . Намагниченность насыщения магнетита равна
. Намагниченность насыщения магнетита равна ![]() Гс [9]. Рассчитанная по формуле Ланжевена намагниченность для этого случая равна
Гс [9]. Рассчитанная по формуле Ланжевена намагниченность для этого случая равна ![]() Гс. Величину скорости ультразвука в магнитной жидкости при отсутствии внешнего магнитного поля приняли равной
Гс. Величину скорости ультразвука в магнитной жидкости при отсутствии внешнего магнитного поля приняли равной ![]() . Для воды
. Для воды ![]() , поэтому вычисленные значения времен релаксации равны
, поэтому вычисленные значения времен релаксации равны ![]() и
и ![]() .
.
На рис. 1 изображена теоретическая кривая для скорости медленной волны по формуле (10) без учета вязкости в зависимости от угла ![]() . Данная волна проявляет анизотропию, причем скорость перпендикулярно магнитному полю больше, чем параллельно полю. Это очевидно, так как в пределе
. Данная волна проявляет анизотропию, причем скорость перпендикулярно магнитному полю больше, чем параллельно полю. Это очевидно, так как в пределе ![]() из (13) получается
из (13) получается ![]() , что превосходит скорость волны альфвеновского типа
, что превосходит скорость волны альфвеновского типа ![]() при
при ![]() , которая равна скорости медленной волны при
, которая равна скорости медленной волны при ![]() . Это совпадает с данными вычислительного эксперимента, которые изображены на рис.1.
. Это совпадает с данными вычислительного эксперимента, которые изображены на рис.1.

Рис. 1 Скорость медленной магнитозвуковой волны в зависимости от угла ![]() .
.
При действии внешнего магнитного поля медленная волна была обнаружена в магнитной суспензии, где частицы имеют микронные размеры [12]. В данных экспериментах использовалось сильное магнитное поле и для частиц применимо однодоменное состояние. В теории магнитной жидкости с вмороженной намагниченностью были объяснены экспериментальные данные по скорости медленной волны: около ![]() [5]. В [12] эксперименты проведены только для распространения волн вдоль поля
[5]. В [12] эксперименты проведены только для распространения волн вдоль поля ![]() . В теории магнитной жидкости с вмороженной намагниченностью [5,13] медленная волна не распространяется перпендикулярно магнитному полю, а в теории магнитной жидкости с внутренним вращением распространяется в случаях
. В теории магнитной жидкости с вмороженной намагниченностью [5,13] медленная волна не распространяется перпендикулярно магнитному полю, а в теории магнитной жидкости с внутренним вращением распространяется в случаях ![]() и
и ![]() (13). Это является еще одним отличием двух теорий.
(13). Это является еще одним отличием двух теорий.
ЗАКЛЮЧЕНИЕ
Таким образом, показано, что в модели магнитной жидкости с внутренним вращением существуют три гидродинамические моды, как и в теории магнитной жидкости с вмороженной намагниченностью [5]. Геометрия задачи отличается от [4], но это не влияет на получаемые решения в модели магнитной жидкости с внутренним вращением. Из полученных в данной работе выражений следует, при распространении быстрой и медленной волн возмущается плотность и, поэтому проявляется анизотропия скорости и коэффициента поглощения звука. Модифицированная волна альфвеновского типа – это распространение возмущений компонент скорости и намагниченности, которые перпендикулярны направлению волнового вектора, т. е. является поперечной волной.
ЛИТЕРАТУРА
1. Sokolov V.V., Tolmachov V.V. Wave Propagation in Magnetic Fluid with Frozen Magnetization // Sev. Int. Conf. onMagn. Fluids : Abstracts. India, Bhavnagar, 1995. P. 194-195.
2. Шлиомис М.И. К гидродинамике жидкости с внутренним вращением // Журнал экспериментальной и теоретической физики. 1966. Т. 51. Вып. 1 (7). С. 258-265.
3. Зайцев В.М., Шлиомис М.И. Увлечение ферромагнитной суспензии вращающимся полем // Журнал прикладной механики и технической физики. 1969. № 5. С. 11-16.
4. Райхер Ю.Л., Шапошников И.Г. О спектре собственных колебаний ферромагнитной жидкости // Физические свойства и гидродинамика ферромагнетиков: сб. науч. тр. / Уральский научный центр, Академия наук СССР. Свердловск, 1977. С. 20-27.
5. Sokolov V.V. Wave Propagation in Magnetic Nanofluids (A Reiew) // Acoustical Physics. 2010. Vol. 56. No. 6. P. 972-988. DOI : 10.1134/S1063771010060229
6. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1982. 624 с.
7. Резибуа П., Де Леенер М. Классическая кинетическая теория жидкостей и газов. М.: Мир, 1980. 424 с. [Resibois P., De Leener M. Classical Kinetic Theory of Fluids. NewYork: JohnWileyandSons, 1977].
8. Буров В.А., Алексеенко Н.В., Румянцева О.Д. Многочастотное обобщение алгоритма Новикова для решения обратной двумерной задачи рассеяния // Акустический журнал. 2009. T. 55. № 6. C. 784-798.
9. Фертман В.Е. Магнитные жидкости: справочное пособие. Мн.: Высш. шк., 1988. 184 с.
10. Шлиомис М.И. Эффективная вязкость магнитных суспензий // Журнал экспериментальной и теоретической физики. 1971. Т. 61. Вып. 6 (12). C. 2411-2418.
11. Hornowski T. Ultrasonic Properties of EMG-605 Magnetic Liquid // Proc. of SPIE. 2005. Vol. 5828. P. 205-212. DOI : http://dx.doi.org/10.1117/12.612810
12. Nahmad-Molinari Y, Arancibia-Bulnes C.A., Ruiz-Suarez J.C. Sound in a Magnetorheological Slurry // Phys. Rev. Lett. 1999. Vol. 82. P. 727-730.
13. Овчинников И.Э., Соколов В.В. Влияние внешнего магнитного поля на скорости распространения магнитозвуковых волн в магнитной жидкости // Акустический журнал. 2009. T. 55. № 3. C. 356-361.
Публикации с ключевыми словами: ультразвук, магнитная жидкость, намагниченность, наночастицы, магнетит
Публикации со словами: ультразвук, магнитная жидкость, намагниченность, наночастицы, магнетит
Смотри также:
- Методы лечения синдрома диабетической стопы. Обзор
- Исследование процесса ультразвуковой капиллярной подачи жидких лекарственных водоподобных препаратов на излучающую поверхность ультразвукового волновода
- Поверхностные магнитостатические волны в плёнках кубических ферритов, ориентированных вдоль кристаллографических плоскостей симметрии
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



