научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2012
DOI: 10.7463/0812.0431723
УДК 519.6
Россия, МГТУ им. Н.Э.Баумана
Введение
Относительно новым и быстро развивающимся классом методов глобальной оптимизации является класс эвристических методов. Среди методов этого класса выделяют эволюционные и поведенческие (имитационные) методы, последние из которых и рассматриваются в данной работе [1]. Поведенческие методы основаны на моделировании коллективного поведения самоорганизующихся живых или неживых систем, взаимодействующие элементы которых называют агентами. Ключевыми идеями поведенческих методов являются децентрализованность, взаимодействие агентов, простота их поведения [2].
Для повышения эффективности поведенческих методов глобальной оптимизации в настоящее время используют два основных подхода ‑ гибридизация и метаоптимизация.
При гибридизации объединяют либо различные методы, либо одинаковые методы, но с различными значениями свободных параметров, так чтобы эффективность одного метода компенсировала слабость другого. Известно несколько классификаций алгоритмов гибридизации поведенческих методов глобальной оптимизации [3 - 5]. Наиболее известна одноуровневая классификация Ванга (X. Wang), в соответствии с которой выделяют гибридизацию по схеме вложенных (embedded) методов, гибридизацию типа препроцессор /постпроцессор (preprocessor / postprocessor) и коалгоритмическую (co-algorithms) гибридизацию. В работе используем гибридизацию вложением, точнее говоря, высокоуровневую и низкоуровневую гибридизации вложением.
Высокоуровневая гибридизация вложением (high-levelembeddedhybridization) предполагает слабую связь объединяемых методов. Комбинируемые методы в этом случае сохраняют значительную автономию, так что в итоговом методе относительно легко выделить каждый из них (см., например, [6]). При низкоуровневой гибридизации вложением (low-levelembeddedhybridization) комбинируемые методы интегрированы настолько сильно, что выделить составляющие итогового метода обычно невозможно, т.е. низкоуровневая гибридизация порождает, по сути, новый метод.
Поведенческие методы глобальной оптимизации и, в особенности, гибридные методы имеют большое число свободных параметров. От значений этих параметров часто в значительной мере зависит эффективность методов. С другой стороны обычно отсутствуют правила выбора значений указанных параметров. Поэтому одним из основных путей повышения эффективности поведенческих методов является разработка алгоритмов адаптации значений их свободных параметров к особенностям конкретной задачи оптимизации либо к особенностям некоторого класса задач оптимизации ‑ метаоптимизация поведенческих методов.
Наиболее известные классификации алгоритмов метаоптимизации представлены в работах [7, 8]. Ограничимся классификацией Ибена (A.E. Eiben), в соответствии с которой выделяют алгоритмы настройки параметров (parametertuning) и алгоритмы управления параметрами (parametercontrol) [7]. Первые из указанных алгоритмов разделяют на алгоритмы однократной настройки и алгоритмы перманентной настройки. Идея алгоритмов однократной настройки параметров (one-timeparametertuning), используемых в нашей работе, состоит в том, что программу, реализующую рассматриваемый метод оптимизации, выполняют при различных значениях его свободных параметров на большом числе задач оптимизации того или иного класса. На основе результатов исследования выбирают значения параметров с наилучшими показателями эффективности.
Целью работы является разработка, настройка параметров и исследование эффективности оригинального гибридного алгоритма глобальной оптимизации на основе метода роя частиц (ParticleSwarmOptimization, PSO) [9]. Метод PSOв силу его эффективности и высокой степени разработанности широко используют в качестве базового метода при построении многих гибридизаций. Приведем несколько примеров.
Метод PSO-EO [10] представляет собой гибридизацию канонического метода PSO с методом экстремальной оптимизации (ExtremelyOptimization, ЕО) [11]. Гибридизация метода PSO и метода заряженных частиц (ChargedSystemSearch, CSS) представлена в работах [12, 13]. Комбинированный метод IBPSO, представляющий собой объединение бинарного метода PSOи метода искусственной иммунной системы (ArtificialImmuneSystem, AIS), предложен в работе [14]. Для диверсификации поиска и повышения тем самым вероятности локализации глобального экстремума сложных многоэкстремальных функций, в работе [15] предложена гибридизация метода PSO и широко известного метода дифференциальной эволюции (DifferentialEvolution, DE) – гибридный метод PSO-DE. Метод HPSI, основанный на гибридизации методов PSO и искусственной иммунной системы, представлен в работе [16]. Гибридный метод BSO [17] использует комбинацию метода PSOи метода светлячков (Glow-wormSwarmOptimization, GSO). Метод PSACO [18] есть не что иное, как гибридизация метода PSO и метода колонии муравьев (AntColonyOptimization, ACO), как метода локального поиска. Гибридизация метода PSOи метода сорняков (InvasiveWeedOptimization, IWO) рассмотрена в работе [19].
В первом разделе работы дана постановка задачи глобальной оптимизации, а также приведены краткие описания базовых методов роя частиц, эволюции разума и клональной селекции. Во втором разделе представлена гибридизация указанных методов и описание гибридного метода, названного нами MEPSI(MindEvolution, ParticleSwarm, Immune). Третий раздел посвящен задаче настройки свободных параметров метода HPSI, на основе которого построен метод MEPSI. В четвертом разделе представлены результаты исследования эволюция состояния роя, который порождает метод MEPSI. Целью исследования является метаоптимизация метода. В пятом разделе представлены результаты исследования эффективности метода MEPSI, выполненного на известных тестовых функциях Шекеля и Растригина. Шестой раздел представляет аналогичные результаты, полученные при решении методов MEPSI семи- и тридцати восьми атомной задачи кластеризации Леннарда-Джонсона. В заключении сформулированы основные результаты работы и перспективы ее развития.
1. Постановка задачи и схема методов роя частиц, эволюции разума и клональной селекции
Рассматриваем задача глобальной безусловной оптимизации целевой функции ![]() в
в ![]() -мерном арифметическом пространстве
-мерном арифметическом пространстве ![]()
 .
.
Поскольку в основу метода MEPSIположен метод роя частиц, агенты в котором называют частицами, говорим далее о рое частиц и обозначаем этот рой ![]() , где
, где ![]() ‑ размер роя (число частиц в нем). В дискретный момент времени
‑ размер роя (число частиц в нем). В дискретный момент времени ![]() координаты частицы
координаты частицы ![]() в пространстве поиска определяет вектор
в пространстве поиска определяет вектор ![]() , а ее «скорость» - вектор
, а ее «скорость» - вектор ![]() .
.
1.1. Канонический метод роя частиц
Итерации в каноническом методе PSOвыполняем по схеме [9]
![]() , (1)
, (1)
![]() . (2)
. (2)
Здесь ![]() - свободные параметры метода;
- свободные параметры метода; ![]() ‑
‑ ![]() -мерный вектор случайных чисел, равномерно распределенных в интервале
-мерный вектор случайных чисел, равномерно распределенных в интервале ![]() ;
; ![]() ‑ символ прямого произведения векторов;
‑ символ прямого произведения векторов; ![]() - вектор координат частицы
- вектор координат частицы ![]() , соответствующий наилучшему значению целевой функции
, соответствующий наилучшему значению целевой функции ![]() , достигнутому ею за время поиска
, достигнутому ею за время поиска ![]() :
:
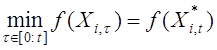 ; (3)
; (3)
![]() - вектор координат соседней с данной частицы с наилучшим за то же время значением функции
- вектор координат соседней с данной частицы с наилучшим за то же время значением функции ![]() :
:
 ; (4)
; (4)
![]() - множество номеров частиц, являющихся соседями данной частицы
- множество номеров частиц, являющихся соседями данной частицы ![]() .
.
Свободный параметр ![]() определяет вес «инерционных» свойств частицы (при
определяет вес «инерционных» свойств частицы (при ![]() ее движение, очевидно, замедляется). Рекомендуемое значение параметра равно
ее движение, очевидно, замедляется). Рекомендуемое значение параметра равно ![]() =0,7298. Значения параметров
=0,7298. Значения параметров ![]() определяют, соответственно, относительные веса «когнитивной» и «социальной» компонент в формуле (2).Рекомендуемые значения параметров равны
определяют, соответственно, относительные веса «когнитивной» и «социальной» компонент в формуле (2).Рекомендуемые значения параметров равны ![]() 1,49618. Соседство частиц понимаем в смысле используемой топологии соседства частиц (swarmtopology) [9].
1,49618. Соседство частиц понимаем в смысле используемой топологии соседства частиц (swarmtopology) [9].
Схема канонического методаPSO имеет следующий вид.
1) Задаем значения свободных параметров метода и инициализируем рой. Полагаем счетчик числа итераций ![]() .
.
2) Для каждой из частиц роя ![]() по формуле (3) находим лучшую локальную позицию
по формуле (3) находим лучшую локальную позицию ![]() , а по формуле (4) - глобально лучшую позицию
, а по формуле (4) - глобально лучшую позицию ![]() .
.
3) По формулам (1), (2) находим новые позиции всех частиц роя ![]() , а также их новые «скорости»
, а также их новые «скорости» ![]() ;
; ![]() .
.
4) Проверяем выполнение условия окончания итераций. Если это условие выполнено, то завершаем итерации, в противном случае полагаем ![]() и переходим к шагу 2.
и переходим к шагу 2.
Инициализация роя заключается в задании начальных позиций ![]() и скоростей
и скоростей ![]() всех
всех ![]() частиц. Обычно позиции
частиц. Обычно позиции ![]() принимают случайными, равномерно распределенными в некотором параллелепипеде
принимают случайными, равномерно распределенными в некотором параллелепипеде
П=![]() , (5)
, (5)
где ![]() - заданные константы. Начальные скорости частиц также инициализируют случайными значениями.
- заданные константы. Начальные скорости частиц также инициализируют случайными значениями.
В качестве условий окончания итераций используют типичные для поведенческих методов оптимизации условия: достижение максимально допустимого числа итераций ![]() ; стагнация итерационного процесса (отсутствие улучшения значений целевой функции на протяжении некоторого числа итераций) и так далее.
; стагнация итерационного процесса (отсутствие улучшения значений целевой функции на протяжении некоторого числа итераций) и так далее.
Обзор большого числа модификаций канонического метода PSO представлен, например, в работе [9].
1.2. Метод эволюции разума
Концепция метода эволюции разума (Mind Evolutionary Computation, MEC) предложена в работе [20]. Метод MEC моделирует скорее некоторые аспекты поведения человека в обществе, чем, как можно было бы предположить, работу человеческого мозга.
Мультипопуляция метода MEC состоит из наборов лидирующих групп (superiorgroups) ![]() и отстающих групп (temporarygroups)
и отстающих групп (temporarygroups) ![]() , содержащих для простоты записи по
, содержащих для простоты записи по ![]() групп (субпопуляций)
групп (субпопуляций) ![]() каждая. Числа индивидов в указанных группах полагаем одинаковыми и равными
каждая. Числа индивидов в указанных группах полагаем одинаковыми и равными ![]() . Каждая из групп имеет свою коммуникационную среду, называемую локальной доской объявлений (localbillboard). Обозначим эти доски
. Каждая из групп имеет свою коммуникационную среду, называемую локальной доской объявлений (localbillboard). Обозначим эти доски ![]() ,
, ![]() соответственно. Кроме того, вся мультипопуляция
соответственно. Кроме того, вся мультипопуляция ![]() имеет общую, глобальную доску объявлений (globalbillboard)
имеет общую, глобальную доску объявлений (globalbillboard) ![]() . Если далее в обозначениях группы и соответствующих локальных досок объявлений индексы
. Если далее в обозначениях группы и соответствующих локальных досок объявлений индексы ![]() опущены, то имеется в виду произвольная из этих групп и их досок объявлений.
опущены, то имеется в виду произвольная из этих групп и их досок объявлений.
Исходная версия метода MEC, названная авторами простым методом эволюции разума (Simple MEC, SMEC), построена на основе операций инициализации групп, локальных состязаний (similar-taxis) и диссимиляции (dissimilation).
Операция инициализации групп создает наборы групп ![]() ,
, ![]() и размещает их в области поиска. Рассмотрим схему операции на примере группы
и размещает их в области поиска. Рассмотрим схему операции на примере группы ![]() ,
, ![]() .
.
1) Генерируем случайный вектор ![]() , компоненты которого равномерно распределены в параллелепипеде (5). Отождествляем этот вектор с индивидом
, компоненты которого равномерно распределены в параллелепипеде (5). Отождествляем этот вектор с индивидом ![]() группы
группы ![]() .
.
2) Определяем начальные координаты остальных индивидов данной группы ![]() по формуле
по формуле
![]() ,
, ![]() , (6)
, (6)
т.е. размещаем случайным образом вокруг индивида![]() в соответствии с нормальным законом распределения, имеющим по всем
в соответствии с нормальным законом распределения, имеющим по всем ![]() координатам нулевое математическое ожидание и среднее квадратичное отклонение
координатам нулевое математическое ожидание и среднее квадратичное отклонение ![]() (свободный параметр метода).
(свободный параметр метода).
Операция локальных состязаний реализует локальный поиск минимума целевой функции ![]() каждой из групп
каждой из групп ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Рассмотрим в качестве примера схему этой операции для группы
. Рассмотрим в качестве примера схему этой операции для группы ![]() .
.
1) С доски объявлений ![]() берем информацию о текущем индивиде-победителе группы
берем информацию о текущем индивиде-победителе группы ![]() . Пусть это будет индивид
. Пусть это будет индивид ![]() ,
, ![]() .
.
2) Определяем новые координаты остальных индивидов ![]() ,
, ![]() ,
, ![]() данной группы по правилу вида (6), т.е. размещаем случайным образом вокруг победителя в соответствии с нормальным законом распределения.
данной группы по правилу вида (6), т.е. размещаем случайным образом вокруг победителя в соответствии с нормальным законом распределения.
3) Вычисляем новые счета (scores)индивидов группы ![]() ,
, ![]() , где инверсия значений целевой функции использована, поскольку далее речь идет о максимизации счета, а функция
, где инверсия значений целевой функции использована, поскольку далее речь идет о максимизации счета, а функция ![]() подлежит минимизации.
подлежит минимизации.
4) Определяем нового победителя группы ![]() ,
, ![]() , т.е. индивида данной группы, который имеет максимальный текущий счет:
, т.е. индивида данной группы, который имеет максимальный текущий счет:
 .
.
5) Заносим информацию о новом победителе группы ![]() на доски объявлений
на доски объявлений ![]() ,
, ![]() .
.
Операция диссимиляции управляет глобальным поиском. Схема операции имеет следующий вид.
1) С глобальной доски объявлений ![]() считываем счета
считываем счета ![]() ,
, ![]() ,
, ![]() ,
, ![]() всех групп (т.е. текущие счета победителей этих групп).
всех групп (т.е. текущие счета победителей этих групп).
2) Выполняем сравнение указанных счетов между собой. Если счет некоторой лидирующей группы ![]() меньше счета одной из отстающих групп
меньше счета одной из отстающих групп ![]() , то последняя группа занимает место группы
, то последняя группа занимает место группы ![]() во множестве лидирующих групп, а группа
во множестве лидирующих групп, а группа ![]() ‑ место группы
‑ место группы ![]() среди отстающих групп. Если счет группы
среди отстающих групп. Если счет группы ![]() ниже счетов всех лидирующих групп, то удаляем группу
ниже счетов всех лидирующих групп, то удаляем группу ![]() из популяции.
из популяции.
3) С помощью операции инициализации взамен каждой из удаленных групп инициализируем новую группу.
В методе SMEC операции локальных состязаний и диссимиляции итерационно повторяются до тех пор, пока имеет место увеличение максимального счета лидирующих групп. При прекращении роста этого счета, решение задачи, соответствующее победителю лучшей из лидирующих групп, объявляем точкой глобального экстремума.
Известно значительное число модификаций метода SMEC, направленных на повышение его эффективности [21].
1.3. Метод клональной селекции
Клональная селекция является одним из механизмов искусственных иммунных систем, которые можно определить, как информационную технологию, использующую понятия, аппарат и некоторые результаты теоретической иммунологии для решения прикладных задач и, в частности, для решения задач оптимизации [22]. Биологическим прототипом AIS является иммунная система человека и обработка информации в ней молекулами белков (пептидов).
Основной задачей иммунной системы является распознавание и уничтожение любого чужеродного агента, которым может быть болезнетворный микроорганизм, инородное тело, ядовитое вещество или переродившаяся клетка самого организма. Агенты, воспринимаемые иммунной системой как чужеродные, называют антигенами (antigens). В ответ на появление в организме антигенов иммунная система образует специальные, реагирующие с ними антитела (antibodies).
Схема метода клональной селекции (clonalselectionalgorithm, CSA) имеет следующий вид.
1) Инициализируем популяцию антител ![]() (решений), включающую в себя субпопуляцию, так называемых, клеток памяти
(решений), включающую в себя субпопуляцию, так называемых, клеток памяти![]() .
.
2) Вычисляем значения целевой функции для всех агентов популяции ![]() и выбираем из нее
и выбираем из нее ![]() лучших агентов. Клонируем лучших агентов во временную популяцию С так, чтобы общее число клонов было равно
лучших агентов. Клонируем лучших агентов во временную популяцию С так, чтобы общее число клонов было равно ![]() .
.
3) Всех клонов из популяции Cподвергаем мутации, с вероятностью обратно пропорциональной соответствующим значениям целевой функции. Из мутированных агентов формируем популяцию ![]() . Вычисляем значения целевой функции для всех агентов популяции
. Вычисляем значения целевой функции для всех агентов популяции ![]() и удаляем из этой популяции агентов, близких к агентам популяции С.
и удаляем из этой популяции агентов, близких к агентам популяции С.
4) Выбираем ![]() лучших агентов популяции
лучших агентов популяции ![]() и помещаем в популяцию клеток памяти
и помещаем в популяцию клеток памяти ![]() . Здесь
. Здесь ![]() - степень селекции (selection rate). Расширяем популяцию
- степень селекции (selection rate). Расширяем популяцию ![]() агентами популяции
агентами популяции ![]() .
.
5) Выполняем, так называемое сетевое сжатие популяции ![]() ‑ исключаем из нее
‑ исключаем из нее ![]() часть худших агентов;
часть худших агентов; ![]() .
.
6) Выполняем операцию клонального сжатия популяции ‑ заменяем ![]() часть худших агентов популяции
часть худших агентов популяции ![]() новыми, случайно сгенерированными агентами;
новыми, случайно сгенерированными агентами; ![]() .
.
7) Если условие окончания итераций не выполнено, то переходим к шагу 2.
Принципиальные идеи метода CSAзаключаются в удалении агентов из популяции (шаг 3), позволяющем уменьшить вероятность сходимости к локальному минимуму целевой функции, клонировании лучших агентов, а также их мутации с вероятностью, зависящей от соответствующих значений целевой функции.
2. Метод MEPSI
В основу метода MEPSIположен упомянутый выше метод HPSI[16], представляющий собой гибридизацию методов PSO и иммунной системы. Основная идея метода HPSI состоит в использовании частицами механизма клонального сжатия (п.1.3), который повышает диверсификационные свойства метода, предотвращает его преждевременную сходимость и повышает вероятность локализации глобального экстремума.
Схема метода HPSI имеет следующий вид.
1) Инициализируем роя частиц ![]() по правилам метода PSO (п.1.1).
по правилам метода PSO (п.1.1).
2) Вычисляем значения целевой функции ![]() для всех частиц роя.
для всех частиц роя.
3) Для каждой из частиц ![]() находим векторы
находим векторы ![]() ,
, ![]() .
.
4) По формулам (1), (2) производим пересчет скоростей и позиций частиц.
5) Случайным образом выбираем из популяции ![]() частиц и выполняем для них операцию клонального сжатия.
частиц и выполняем для них операцию клонального сжатия.
6) Пока условие окончания итераций не выполнено, возвращаемся к шагу 2
Операция клонального сжатия «разбрасывает» частицы роя по пространству поиска. Называем поэтому далее эту операцию взрывом роя.
Схему метода MEPSIопределяет следующая последовательность шагов.
1) По правилам улучшенного метода MECинициализируем рой, содержащий ![]() групп частиц по
групп частиц по ![]() агентов в каждой, таким образом, что частицы группы
агентов в каждой, таким образом, что частицы группы ![]() принадлежат параллелепипеду
принадлежат параллелепипеду ![]() ;
;  .
.
2) Выполняем ![]() итераций метода HPSI, в течение которых каждые
итераций метода HPSI, в течение которых каждые ![]() итераций производим взрыв роя. В случае, если некоторая частица вылетает за границы параллелепипеда П, возвращаем ее на эту границу, а скорость инвертируем.
итераций производим взрыв роя. В случае, если некоторая частица вылетает за границы параллелепипеда П, возвращаем ее на эту границу, а скорость инвертируем.
3) Реализуем операцию локальных состязаний.
4) Определяем глобально лучшие частицы каждой из групп ![]() .
.
5) Выполняем сравнение приспособленностей глобально лучших частиц групп и выделяем победителей и аутсайдеров среди групп.
6) Если некоторая группа в течение ![]() итераций занимает среди аутсайдеров последнее место, то удаляем ее из популяции.
итераций занимает среди аутсайдеров последнее место, то удаляем ее из популяции.
7) Если текущее число групп больше чем одна, то переходим к шагу 2.
Свободными параметрами метода MEPSI являются число групп ![]() , размер каждой из групп
, размер каждой из групп ![]() , частота применения операции локальных состязаний
, частота применения операции локальных состязаний ![]() , частота взрывов роя
, частота взрывов роя ![]() , время жизни проигравших групп
, время жизни проигравших групп ![]() . На основании рекомендаций работы [16] принимаем
. На основании рекомендаций работы [16] принимаем ![]() .
.
3. Настройка параметров метода HPSI
Настройка параметров метода HPSIв рамках задачи его метаоптимизации выполнена нами для функций Шекеля и Растригина. Использован мультистарт из 100 запусков. Задача решалась в параллелепипеде ![]() , т.е. размерность вектора варьируемых параметров была принята равной
, т.е. размерность вектора варьируемых параметров была принята равной ![]() .
.
Рассматриваем следующие критерии эффективности метода, вычисление значений которых основано на результатах мультистарта:
![]() ‑ оценка математического ожидания числа итераций до начала процесса стагнации вычислительного процесса;
‑ оценка математического ожидания числа итераций до начала процесса стагнации вычислительного процесса;
![]() ‑ оценка среднеквадратического отклонения того же числа;
‑ оценка среднеквадратического отклонения того же числа;
![]() ‑ оценка математического ожидания числа испытаний до стагнации;
‑ оценка математического ожидания числа испытаний до стагнации;
![]() ‑ оценка среднеквадратического отклонения последнего числа;
‑ оценка среднеквадратического отклонения последнего числа;
![]() ‑ оценка вероятности локализации глобального экстремума с заданной точностью
‑ оценка вероятности локализации глобального экстремума с заданной точностью ![]() (точность алгоритма).
(точность алгоритма).
Функция Шекеля характеризуется наличием нескольких минимумов, число ![]() и глубину которых задает исследователь. В наших экспериментах использовано m=10. В таблице 1 и на иллюстрирующем ее рисунке 1 представлены результаты настройки числа итераций
и глубину которых задает исследователь. В наших экспериментах использовано m=10. В таблице 1 и на иллюстрирующем ее рисунке 1 представлены результаты настройки числа итераций ![]() .
.
Таблица 1.
Настройка метода HPSI: функция Шекеля, варьирование параметра ![]()
Критерий | Величина | ||
30 | 40 | 50 | |
MI | 164 | 164 | 160 |
SI | 14 | 38 | 40 |
ME | 12969 | 12831 | 12247 |
SE | 1144 | 2432 | 2575 |
A | 0,54 | 0,59 | 0,46 |

Рисунок 1 – Настройка метода HPSI: функция Шекеля; варьирование ![]()
Аналогичные результаты, полученные при настройке частоты взрывов ![]() , представлены в таблице 2 и на рисунке 2.
, представлены в таблице 2 и на рисунке 2.
Таблица 2.
Настройка метода HPSII: функция Шекеля, варьирование параметра r
Критерий | Величина r | ||
1 |
|
| |
MI | 111 | 184 | 165 |
SI | 51 | 42 | 47 |
ME | 7132 | 13495 | 12689 |
SE | 3156 | 2809 | 2990 |
A | 0,14 | 0,60 | 0,58 |
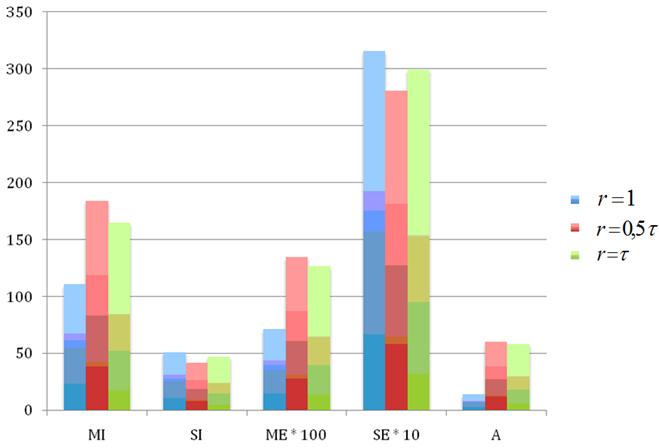
Рисунок 2 – Настройка метода HPSI: функция Шекеля; варьирование ![]()
Представленные результаты показывают, что с ростом времени жизни проигравших групп ![]() , числа испытаний MEи итераций MIвозрастают, а среднеквадратические отклонения указанных величин SE, SIубывают. При этом точность локализации глобального экстремума Aдля
, числа испытаний MEи итераций MIвозрастают, а среднеквадратические отклонения указанных величин SE, SIубывают. При этом точность локализации глобального экстремума Aдля ![]() примерно одинакова, в то время как для
примерно одинакова, в то время как для ![]() уменьшается по сравнению с указанными вариантами примерно на 25 %. Результаты исследования показывают, что оптимальными по критерию
уменьшается по сравнению с указанными вариантами примерно на 25 %. Результаты исследования показывают, что оптимальными по критерию 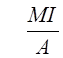 являются значения параметров
являются значения параметров ![]() или
или ![]() при
при ![]() .
.
Функция Растригина характерна наличием большого числа локальных минимумов и плавным спуском к глобальному минимуму в точке ![]() . Результаты, аналогичные результатам, представленным в п. 3.1, приведены в таблицах 3, 4 и на рисунках 3, 4.
. Результаты, аналогичные результатам, представленным в п. 3.1, приведены в таблицах 3, 4 и на рисунках 3, 4.
Таблица 3
Настройка метода HPSI: функция Растригина; варьирование параметра ![]()
Критерий | Величина | ||
30 | 40 | 50 | |
MI | 300 | 315 | 305 |
SI | 126 | 149 | 129 |
ME | 19698 | 20739 | 20143 |
SE | 7906 | 9456 | 8156 |
A | 0,31 | 0,27 | 0,33 |
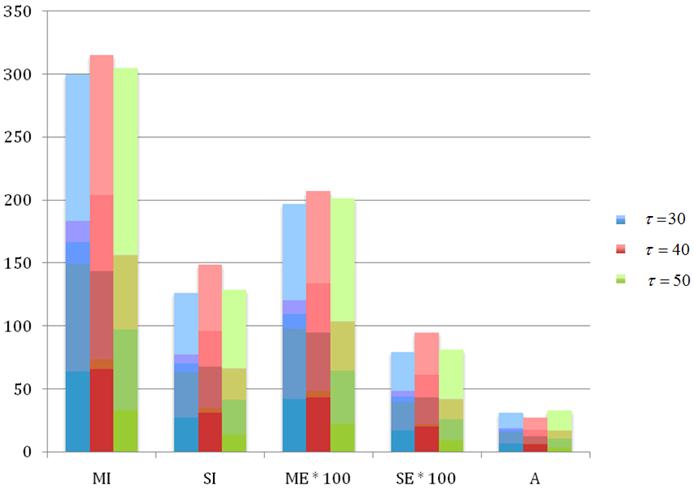
Рисунок 3 – Настройка метода HPSI: функция Растригина; варьирование ![]()
Таблица 4
Настройка метода HPSI: функция Растригина; варьирование параметра ![]()
Критерий | Величина | ||
1 |
|
| |
MI | 109 | 330 | 300 |
SI | 52 | 131 | 126 |
ME | 7405 | 21880 | 19698 |
SE | 3539 | 8587 | 7906 |
A | 0,2 | 0,43 | 0,31 |

Рисунок 4 – Настройка метода HPSI: функция Растригина; варьирование ![]()
Таблица 3 и рисунок 3 показывают, что для функции Растригина все рассматриваемые критерии оптимальности слабо зависят от времени жизни проигравших роев ![]() . Напротив, таблица 4 и рисунок 4 показывают сильную зависимость этих критериев от числа взрывов r. С точки зрения точности алгоритма Aоптимальным значением является
. Напротив, таблица 4 и рисунок 4 показывают сильную зависимость этих критериев от числа взрывов r. С точки зрения точности алгоритма Aоптимальным значением является ![]() .
.
Подведем итоги. Проведенное исследование эффективности метода HPSIпоказывает, что критерии эффективности ![]() в большей степени зависит от частота взрывов rи в меньшей – от частоты удаления проигравших групп
в большей степени зависит от частота взрывов rи в меньшей – от частоты удаления проигравших групп ![]() . Для функции Шекеля варьирование параметра
. Для функции Шекеля варьирование параметра ![]() не приводит к существенным изменениям ни в числе испытаний ME, ни в точности А (таблица 1). Оптимальными оказываются настройки
не приводит к существенным изменениям ни в числе испытаний ME, ни в точности А (таблица 1). Оптимальными оказываются настройки ![]() ,
, ![]() (таблица 2). С точки зрения тех же критериев эффективность метода HPSIдля функции Растригина также слабо зависит от значений параметра
(таблица 2). С точки зрения тех же критериев эффективность метода HPSIдля функции Растригина также слабо зависит от значений параметра ![]() (таблица 3). В то время оптимальное значение параметра
(таблица 3). В то время оптимальное значение параметра ![]() позволяет увеличить точность
позволяет увеличить точность ![]() метода более чем в 20 раз (таблица 4).
метода более чем в 20 раз (таблица 4).
В целом, на основе представленных результатов исследования в качестве оптимальных значений параметров ![]() принимаем значения
принимаем значения ![]() ,
, ![]() .
.
Для изучения качества роя, который порождает метод MEPSI, используем эволюционную оценку состояния (evolutionarystateestimation) [23]. В соответствии с указанной работой введем в рассмотрение следующие величины:
‑ среднее евклидово расстояние частицы ![]() рассматриваемого роя
рассматриваемого роя ![]() до всех остальных частиц этого роя
до всех остальных частиц этого роя
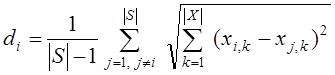 ,
,
‑ минимальное и максимальное расстояние между частицами роя
![]() ,
, ![]() ,
,
‑ среднее евклидово расстояние ![]() между глобально лучшей частицей роя
между глобально лучшей частицей роя ![]() и остальными частицами роя,
и остальными частицами роя,
‑ эволюционный коэффициент (evolutionary factor)
![]()
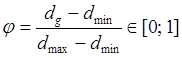 . (7)
. (7)
Из формулы (7) следует, что нулевое значение эволюционного коэффициента соответствует ситуации ![]() , когда все частицы стянуты в окрестность глобально лучшей частицы, то есть ситуации стагнации вычислительного процесса. Напротив, близкие к единице значения величины
, когда все частицы стянуты в окрестность глобально лучшей частицы, то есть ситуации стагнации вычислительного процесса. Напротив, близкие к единице значения величины ![]() означают широкое распределение частиц в области поиска (этап диверсификации поиска).
означают широкое распределение частиц в области поиска (этап диверсификации поиска).
Исследование эволюции состояния роя выполнено для пятимерной функции Растригина (п. 3). Рассматриваем три группы экспериментов:
‑ взрывы на каждой 15-ой итерации (![]() );
);
‑ взрывы на каждой итерации (![]() ),
),
‑ взрывы на каждой 30-ой итерации (![]() ).
).
Целью вычислительных экспериментов является, во-первых, настройка значений указанного параметра и, во-вторых, объяснение причин того или иного поведения эффективности метода MEPSI в функции значений этого параметра.
4.1. Взрывы на каждой 15-ой итерации (![]() )
)
Характер изменения эволюционного коэффициента ![]() в процессе итераций иллюстрируют рисунки 5а, 5б. Величина
в процессе итераций иллюстрируют рисунки 5а, 5б. Величина ![]() на рисунке 5б представляет собой значение целевой функции, соответствующее текущей глобально лучшей частице роя. Таким образом, указанный рисунок иллюстрирует характер сходимости итерационного процесса. Графики функций
на рисунке 5б представляет собой значение целевой функции, соответствующее текущей глобально лучшей частице роя. Таким образом, указанный рисунок иллюстрирует характер сходимости итерационного процесса. Графики функций ![]() ,
, ![]() ,
, ![]() ,
, ![]() представлены в приложении на рисунках П1а – П1г.
представлены в приложении на рисунках П1а – П1г.

а) ![]()

б) ![]()
Рисунок 5 – К эволюции состояния роя: ![]()
Сопоставление рисунков 5а, 5б показывает механизм преодоления роем стагнации вычислительного процесса. Стагнация («полка» на рисунке 5б) завершается процессом уменьшения величины ![]() вследствие взрыва роя (рисунок 5а).
вследствие взрыва роя (рисунок 5а).
4.2. Взрывы на каждой итерации (![]() )
)
В п. 3 была показана неэффективность данной настройки метода HPSI. Рисунки 6а, 6б, а также соответствующие им рисунки П2а – П2г позволяют объяснить этот эффект.
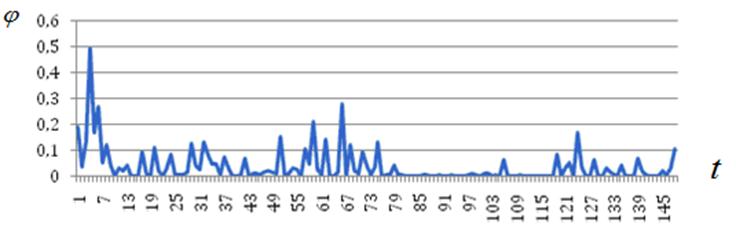
а) ![]()

б) ![]()
Рисунок 6 ‑ Эволюция состояния роя: ![]()
Рисунок 6б показывает, что при ![]() метод вообще не может локализовать глобальный минимум. Рисунки 6а, П2а – П2г объясняют причину такого поведения метода – каждую итерацию взрывы разносят частицы далеко по пространству поиска (см., например, итерации 45, 140) и, поскольку частота взрывов велика, частицы не успевают в промежутки между взрывами локализоваться в окрестности текущей лучшей частицы.
метод вообще не может локализовать глобальный минимум. Рисунки 6а, П2а – П2г объясняют причину такого поведения метода – каждую итерацию взрывы разносят частицы далеко по пространству поиска (см., например, итерации 45, 140) и, поскольку частота взрывов велика, частицы не успевают в промежутки между взрывами локализоваться в окрестности текущей лучшей частицы.
4.3. Взрывы на каждой 30 итерации (![]() )
)
В п. 3 показано, что данная настройка метода является более эффективной по сравнению с предыдущей. Эволюцию роя иллюстрируют рисунки 7а, 7б, а также рисунки П3а – П3г.

а) ![]()

б) ![]()
Рисунок 7 ‑ Эволюция состояния роя: ![]()
Рисунок 7б показывает, что данная настройка метода обеспечивает локализацию глобального минимума. Из рисунков 7а, П3а – П3г следует при ![]() в промежутке между взрывами частицы успевают стянуться в окрестность текущей лучшей частицы.
в промежутке между взрывами частицы успевают стянуться в окрестность текущей лучшей частицы.
5. Исследование эффективности метода MEPSI
Исследование эффективности метода MEPSIвыполнено на тестовых функциях Шекеля и Растригина при следующих значениях свободных параметров метода: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Для тех же тестовых функций выполнено исследование эффективности методов роя частиц PSO и гибридного метода HPSI. Во всех случаях использован мультистарт из 100 запусков соответствующей программы. Рассматриваем критерии эффективности метода, приведенные в п. 3. Кроме того, в качестве критерия эффективности метода используем оценку относительного числа испытаний
. Для тех же тестовых функций выполнено исследование эффективности методов роя частиц PSO и гибридного метода HPSI. Во всех случаях использован мультистарт из 100 запусков соответствующей программы. Рассматриваем критерии эффективности метода, приведенные в п. 3. Кроме того, в качестве критерия эффективности метода используем оценку относительного числа испытаний
 , (8)
, (8)
которая характеризует надежность алгоритма, поскольку более высоким значениям величины (8) соответствует меньший разброс результатов мультистарта.
5.1. Функция Шекеля
Как и в п. 3.1, использованы значения параметров функции ![]() , m=10. Основные результаты исследования представлены в таблице 5, которую иллюстрируют рисунки 8а – 8г.
, m=10. Основные результаты исследования представлены в таблице 5, которую иллюстрируют рисунки 8а – 8г.
Таблица 5
Эффективность метода MEPSI: функция Шекеля
Критерий | Метод | ||
PSO | HPSI | MEPSI | |
MI | 142 | 175 | 321 |
SI | 8 | 34 | 27 |
ME | 11754 | 13308 | 132230 |
SE | 685 | 2264 | 13172 |
A | 0,38 | 0,48 | 0,82 |
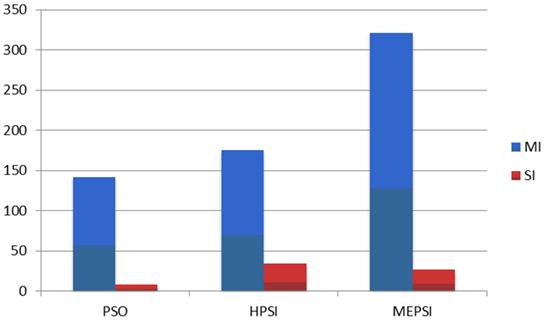
а) критерии MI и SI

б) критерии ME и SE

в) критерий A
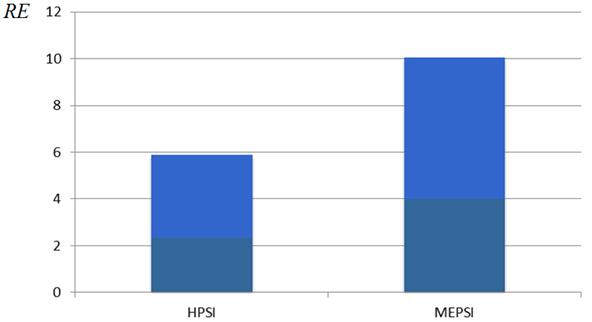
г) критерий RE
Рисунок 8 – Эффективность алгоритма MEPSI: функции Шекеля
Таблица 5 и рисунки 8а – 8в показывают, что по критерию Aпревосходство метода MEPSIнад методами PSOи HPSIдостигает почти 100%. Однако при этом имеет место также почти 100% увеличение числа итераций MIи числа испытаний ME. Примечательно, что среднеквадратическое отклонение указанных величин ниже, чем у базового алгоритма HPSI. Значительный интерес представляет рисунок 8г, показывающий значительное превосходство алгоритма MEPSIнад алгоритмом HPSIпо критерию надежности RE.
Результаты исследования эффективности метода MEPSI для функции Растригина представлены в таблице 6 и на иллюстрирующих ее рисунках 9а –9г. Аналогично п. 3.2, исследование выполнено для вектора варьируемых параметров размерности ![]() .
.
Таблица 6
Эффективность метода MEPSI: функция Растригина
Критерий | Метод | ||
PSO | HPSI | MEPSI | |
MI | 196 | 294 | 306 |
SI | 57 | 134 | 23 |
ME | 13522 | 19327 | 122678 |
SE | 4086 | 8502 | 12990 |
A | 0,2 | 0,7 | 0,53 |
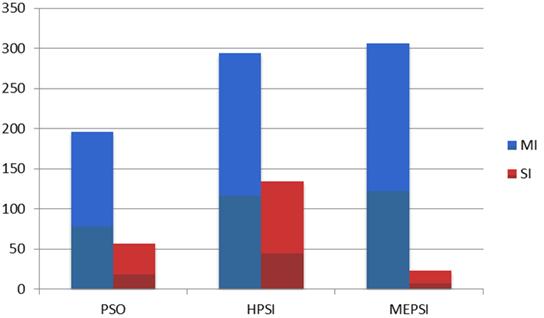
а) критерии MI и SI

б) критерии ME и SE
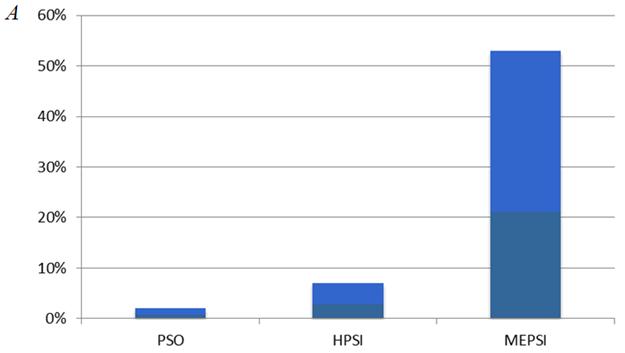
в) критерий A
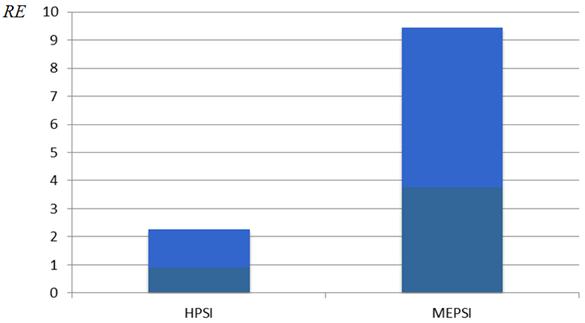
г) критерий RE
Рисунок 9 – К эффективности алгоритма MEPSI: функции Растригина
Представленные результаты показывают, что по сравнению с методом HPSI для функции Растригина метод MEPSIобеспечивает почти в восемь раз более высокую вероятность локализации глобального экстремума, чем для функции Шекеля (критерий A). При этом аналогично пункту 4.1 наблюдается рост числа итераций и рост числа испытаний (критерии MI и ME). Следует заметить, что разница между величинами MI и ME для алгоритмов MEPSI и HPSIв данном случае не столь велика, как для функции Шекеля. Надежность метода MEPSIиллюстрирует рисунок 9г, показывающий значительно большее превосходство данного метода над базовым методом HPSI по сравнению со случаем функции Шекеля.
6. Задача атомной кластеризации Леннарда-Джонса
Под задачей Леннарда-Джонса понимают задачу нахождени координат атомов в молекулярной системе, которые обеспечивают минимум потенциальной энергии этой сисетмы. Потенциальная энергия Леннарда-Джонса играет ключевую роль в определении стабильности высокомолекулярных соединений, таких как, например, белки. Главная сложность задачи Леннарда-Джонсона заключается в мультимодальности целевой функции и высокой размерности вектора варьируемых параметров [24, 25]. Вследствие практической важности и высокой сложности задача широко используется в качестве тестовой для алгоритмов глобальной оптимизации.
Пусть ![]() вектор координат атома
вектор координат атома ![]() в трехмерном евклидовом пространстве
в трехмерном евклидовом пространстве ![]() , а
, а ![]() ‑
‑ ![]() -вектор координат всех атомов в N-атомном кластере
-вектор координат всех атомов в N-атомном кластере ![]() .
.
LJ-потенциал для пары атомов ![]() определяет формула
определяет формула

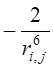 ,
,
где ![]() – евклидово расстояние между атомами
– евклидово расстояние между атомами ![]() .
.
Задача LJ-кластеризации представляет собой задачу глобальной безусловной оптимизации вида
![]() , (9)
, (9)
где целевую функцию ![]() , имеющую смысл суммарной потенциальной энергии кластера, определяет выражение
, имеющую смысл суммарной потенциальной энергии кластера, определяет выражение
 . (10)
. (10)
Задача атомной кластеризации (9), (10) решена нами для семи атомной молекулы (N=7) (мультистарт из 100 запусков) и для тридцати восьми атомной молекулы (N=38). Для оценки точности полученных решений использованы результаты, представленные в работе [6].
6.1. Семиатомный кластер
Результаты решения задачи для ![]() иллюстрирует таблица 7 и рисунок 10. Наилучшее по мультистартам решение
иллюстрирует таблица 7 и рисунок 10. Наилучшее по мультистартам решение ![]() , найденное методом MEPSI, обеспечивает значение потенциальной энергии
, найденное методом MEPSI, обеспечивает значение потенциальной энергии ![]() . Для решения, представленного в работе [25], та же величина равна
. Для решения, представленного в работе [25], та же величина равна ![]() . Таким образом, погрешность наилучшего решения, найденного методом MEPSI, по сравнению с указанным решением не превышает 0,5%.
. Таким образом, погрешность наилучшего решения, найденного методом MEPSI, по сравнению с указанным решением не превышает 0,5%.
Таблица 7
К эффективности метода MEPSI: семиатомная задача Леннарда-Джонса
Критерии оптимальности метода | |||||
MI | SI | ME | SE | RE | A |
332,0 | 25,3 | 133319,3 | 13163,5 | 10,1 | 0,76 |
Рисунок 10 показывает, что относительная погрешность большинства найденных в результате мультистарта решений сконцентрирована в окрестности 2%. Дисперсия погрешности невелика.
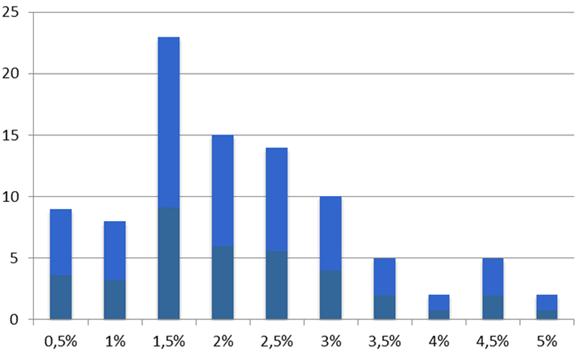
Рисунок 10 ‑ Распределение найденных решений по относительной погрешности: семиатомный кластер
6.2. Тридцати восьми атомный кластер
Решение, представленное в работе [25] для рассматриваемой задачи, равно ![]() , в то время как один запуск алгоритма MEPSI обеспечил
, в то время как один запуск алгоритма MEPSI обеспечил ![]() , то есть погрешность решения, не превышающую 1,7 %. Использовать мультистарт в данном случае оказалось невозможным, поскольку решение задачи на персональном компьютере с процессором 2,0 Ггц, потребовало около четырех суток его непрерывной работы.
, то есть погрешность решения, не превышающую 1,7 %. Использовать мультистарт в данном случае оказалось невозможным, поскольку решение задачи на персональном компьютере с процессором 2,0 Ггц, потребовало около четырех суток его непрерывной работы.
В работе представлен гибридный метод глобальной условной оптимизации MEPSI, представляющий собой модификацию известного метода HPSI, заключающуюся в использовании некоторых операций метода эволюции разума MEC. Таким образом, метод MEPSI представляет собой гибридизацию трех поведенческих методов – роя частиц PSO, эволюции разума MEC и клональной селекции CSA.
Выполнено широкое исследование эффективности предложенного метода на тестовых функциях Шекеля и Растригина. По сравнению с методами PSO и HPSIдля этих функций метод MEPSI показал себя как более точный и надежный. Для обеих функций со 100 % вероятностью решение найдено с погрешностью, не превышающей 0,001 %. Для функции Растригина, имеющей более сложный ландшафт, чем функция Шекеля, наблюдается увеличение эффективности метода MEPSI по критериям точности и надежности. Так с точки зрения точности вычислений Aдля функции Шекеля метод MEPSI оказался в примерно 1,7 раз эффективнее метода HPSI. В тоже время для функции Растригина это превосходство составило почти 7,6 раза. При этом возрастает надежность метода RE – в 1,7 раза для функции Шекеля и в 4,2 раза для функции Растригина.
Наряду с явными преимуществами метода MEPSIнад методом HPSIпо точности и надежности, он является более затратным с точки зрения необходимых вычислительных ресурсов. При этом имеет место интересная особенность ‑ для более сложной функции Растригина относительные затраты ниже, чем для функции Шекеля. Для функции Шекеля метод MEPSIоказался по сравнению с методом HPSI более затратным в 9,9 раз, в то время как для функции Растригина – только в 6,4 раза.
Эффективность метода исследована также на задаче атомной кластеризации Леннарда-Джонса. Для семи атомного кластера метод обеспечил минимальную погрешность, равную 0,5 %. Для 38-атомного кластера в результате одного запуска программы, реализующей метод, решение получено с погрешностью, не превышающей 1,7 %.
В целом, результаты исследования позволяют определить MEPSIкак высокоэффективный метод для широкого класса задач глобальной условной оптимизации.
В развитие работы авторы планируют исследование эффективности метода на более широком классе тестовых функций, распараллеливание метода для различных классов параллельных вычислительных систем, а также его апробацию на практической задаче, сводящейся к задаче глобальной оптимизации.
Литература
1. Luke S. Essentials of Metaheuristics. A Set of Undergraduate Lecture Notes. Department of Computer Science George Mason University. (http://cs.gmu.edu/~sean/book/metaheuristics/Essentials.pdf).
2. Карпенко А.П. Популяционные алгоритмы глобальной поисковой оптимизации. Обзор новых и малоизвестных алгоритмов // Приложение к журналу «Информационные технологии», 2012 (в печати).
3. Wang X. Hybrid nature-inspired computation method for optimization / Doctoral Dissertation. Helsinki University of Technology, TKK Dissertations, Espoo 2009, 161 p.
4. Raidl G.R. A Unified View on Hybrid Metaheuristics // Lecture Notes in Computer Science.– Springer-Verlag, 2006, Vol. 4030,– pp. 1–12.
5. El-Abd, Kamel M. A taxonomy of cooperative search algorithms / Hybrid Metaheuristics: Second International Workshop.- Springer, 2005, Vol. 3636, pp. 32–41.
6. Krasnogor N. Studies on the Theory and Design Space of Memetic Algorithms, Ph.D. Thesis, Faculty of Computing, Mathematics and Engineering, University of the West of England, Bristol, U.K., 2002, 289 p.
7. Eiben A. E., Michalewicz Z., Schoenauer M., Smith J. E. Parameter Control in Evolutionary Algorithms / Parameter Setting in Evolutionary Algorithms.- Springer Verlag, 2007, pp. 19-46.
8. Smith J. E., Fogarty T. C. Operator and parameter adaptation in genetic algorithms // Soft Computing, 1997, No. 1, pp. 81-87.
9. Карпенко А.П., Селиверстов Е.Ю. (2008) Обзор методов роя частиц (PSO) для задачи глобальной оптимизации» // Наука и образование: электронное научно-техническое издание, www.technomag.edu.ru, март, 2009.
10. Chen M.-R., Lu Y.-Z., Luo Q. A novel hybrid algorithm with marriage of particle-swarm optimization and extremely optimization // Optimization Online, May 2007 (http://www.optimization-online.org/ARCHIVE_DIGEST/2007-05.html).
11. Boettcher S., Percus A.G. Nature’s way of optimizing // Artificial Intelligence 2000; No. 119; pp. 275-286.
12. Kaveh A., Talatahari S. Optimal design of skeletal structures via the charged system search algorithm // Structural Multidisciplinary Optimization, 2010, Vol. 37, pp. 893-911.
13. Kaveh A., Talatahar, S. A novel heuristic optimization method: Charged system search // ActaMechanica, 2010, Vol. 213, pp. 267-286.
14. Kennedy J., Eberhart R. C. A discrete binary version of the particle swarm algorithm // Proceedings of 1997 IEEE International Conference on Systems, Man and Cybernetics, 1997, Vol. 5, pp. 4104-4108.
15. Khamsawang S., Boonseng C., Pothiya S. Solving the economic dispatch problem with tabu search algorithm // IEEE International Conference on Industrial Technology 2002, Bangkok, Thailand, pp. 274–278.
16. George AJT, Gray D. Receptor editing during affinity maturation // Immunol Today, 1999, No. 20(4), p. 196.
17. Rossato de Oliveira D., Parpinelli R.S., Lopes H.S. Bioluminescent Swarm Optimization Algorithm / Evolutionary Algorithms, Edited by Eisuke Kita, Publisher: InTech, April 26, 2011, pp. 69-84.
18. Kaveh A., Talatahari S. Engineering optimization with hybrid particle swarm and ant colony optimization // Asian journal of civil engineering, 2009, Vol. 10, №6, pp. 611-628.
19. Mehrabian A. R., Lucas C. A novel numerical optimization algorithm inspired from weed colonization // Ecological Informatics, 2006, Vol. 1, pp. 355–366.
20. Jianchao Zeng, Kai Zha. An Mind Evolution Method for Solving Numerical Optimization Problems // Proc. 3rd World Congress on Intelligent Control and Automation, Hefei, P.R. China. (2000), pp. 126-128.
21. Jie J., Han Ch., Zeng J. An Extended Mind Evolutionary Computation Model for Optimizations // Applied Mathematics and Computation, 2007, No. 185(2), pp. 1038 – 1049.
22. Дасгупта Д. Искусственные иммунные системы и их применение.- Физматлит.- 2006.-344 с.
23. Zhan Z-H., Zhang J. Adaptive Particle Swarm Optimization // Springer-Verlag Berlin, Heidelberg, 2008, ANTS 2008, LNCS 5217, 2008, pp. 227–234.
24. Fan E. Global optimization of Lennard-Jones atomic clusters // MASTER OF SCIENCE (2002), McMaster University, COMPUTING & SOFTWARE, Hamilton, Ontario (http://camo.ici.ro/books/thesis/ellen.pdf)/
25. W. Cai et al. Optimization of Lennard-Jones atomic clusters // Journal of Molecular Structure (Theochem), №579, 2002, pp. 229-234.
Приложение. К эволюции состояния роя в методе MEPSI

а) ![]()
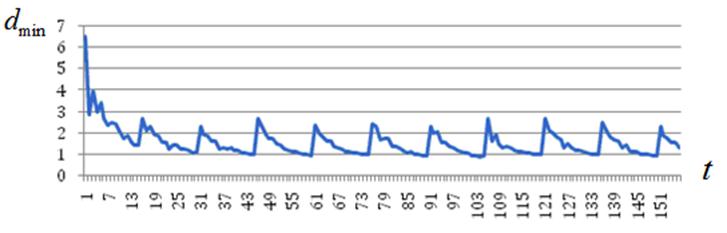
б) ![]()

в) ![]()
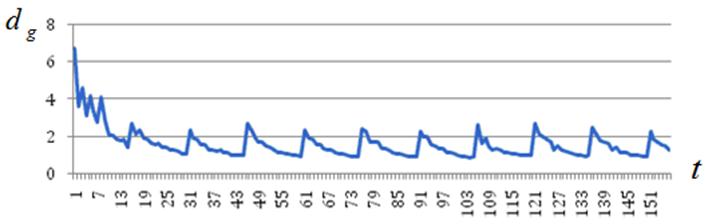
г) ![]()
Рисунок П1 – К эволюции состояния роя: ![]()
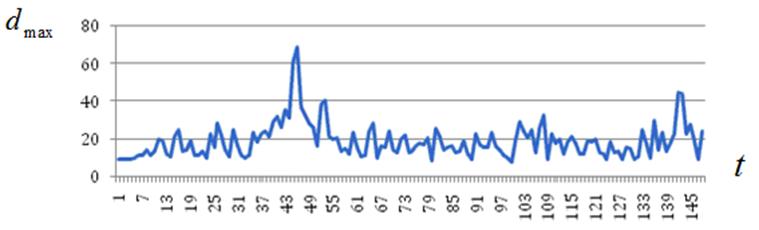
а) ![]()
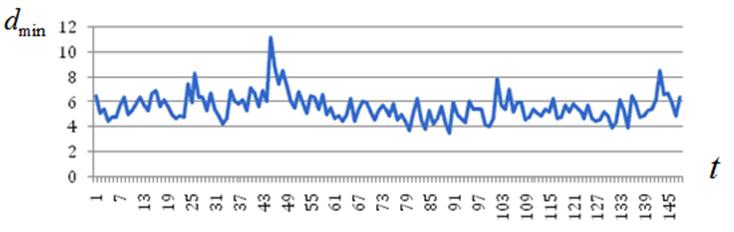
б) ![]()
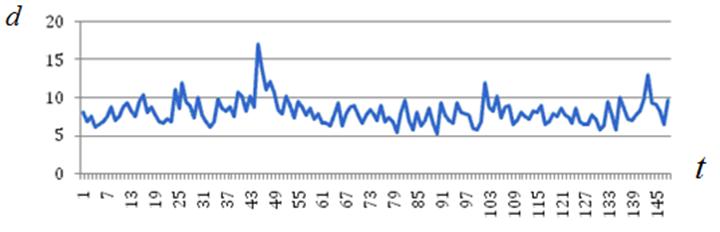
в) ![]()
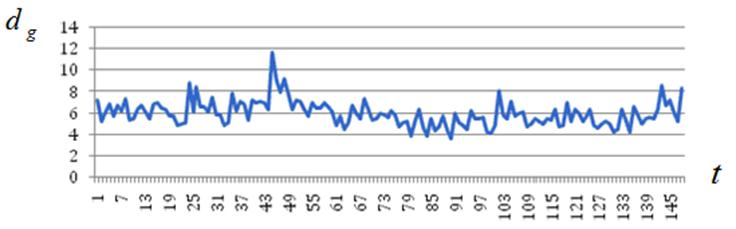
г) ![]()
Рисунок П2 – К эволюции состояния роя: ![]()

а) ![]()
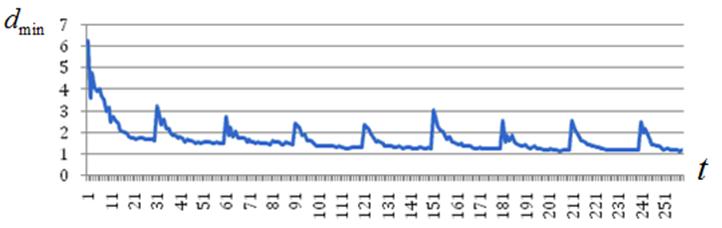
б) ![]()
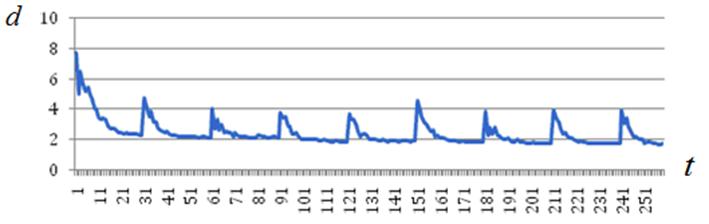
в) ![]()

г) ![]()
Рисунок П3 – К эволюции состояния роя: ![]()
Публикации с ключевыми словами: глобальная оптимизация, метод роя частиц, гибридизация, метод эволюции разума, метод клональной селекции, метаоптимизация
Публикации со словами: глобальная оптимизация, метод роя частиц, гибридизация, метод эволюции разума, метод клональной селекции, метаоптимизация
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



