научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2012
DOI: 10.7463/0812.0428796
УДК 621.378:551.508
Россия, МГТУ им. Н.Э. Баумана
Введение. Развитие промышленности и внедрение новых технологических процессов приводит к все большему загрязнению окружающей среды и в первую очередь земной атмосферы. Наряду с газовыми загрязнениями природного характера в земной атмосфере появляются новые сложные синтетические соединения, не существующие и не образующиеся в природе и не свойственные ей.
Лазерные методы являются наиболее перспективными для оперативного газоанализа (см., например, [1-6]). Если качественный состав газовой смеси известен, то измерение концентраций компонент смеси может быть проведено с использованием перестраиваемого по длине волны источника лазерного излучения, путем регистрации поглощения излучения анализируемой газовой смесью для определенного набора спектральных каналов измерения (см., например, [4-6]). Важным условием применимости такого метода является аддитивность коэффициентов поглощения (в используемых спектральных каналах измерения) отдельных компонент анализируемой газовой смеси.
Для решения задачи определения концентраций газов в многокомпонентных смесях в настоящее время эффективно используются (см., например, [5, 7-9]) метод регуляризации Тихонова с применением различных способов (как детерминистических, так и статистических) выбора параметра регуляризации, метод поиска квазирешений (в ряде работ его называют методом поиска псевдорешений) и метод, основанный на построении байесовской оценки решения.
Однако, существующие методы многокомпонентного газоанализа имеют недостатки (см., например, [10]). Работа авторов [10] была посвящена использованию проекционного метода (не требующего большой априорной информации) в задаче многокомпонентного лазерного газоанализа. Использовался проекционный алгоритм [11,12], разработанный его авторами для обработки одномерных сигналов и двумерных изображений. В [10] показано, что использование проекционного метода для решения системы уравнений лазерного газоанализа обеспечивает достаточно низкий (не более 30 %) уровень погрешностей определения концентраций газов для многокомпонентных смесей даже при значительном шуме измерения (до 10 %). Однако, в работе [10] считалось, что матрица коэффициентов поглощения газовых компонент известна точно.
В настоящей работе рассматривается задача измерения концентраций компонент смеси с использованием перестраиваемого по длине волны источника лазерного излучения при неточно известной матрице коэффициентов поглощения газовых компонент.
Постановка задачи. Задача нахождения концентраций газов из результатов многоспектральных (например, лазерных оптико-акустических) измерений для узкополосного лазерного источника обычно сводится к решению системы линейных алгебраических уравнений вида [5,6] (считаем, что смесь содержит М/2 газовых компонент, измерения проводятся на М длинах волн, а ширина линий генерации лазера много меньше ширины линий поглощения газов):
 , (1)
, (1)
где:
![]() приведенный измеряемый сигнал на длине волны
приведенный измеряемый сигнал на длине волны ![]() (например, для оптико-акустического газоанализатора
(например, для оптико-акустического газоанализатора 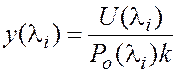 ,
, ![]() - сигнал, измеряемый оптико-акустическим детектором;
- сигнал, измеряемый оптико-акустическим детектором; ![]() - мощность излучения лазера;
- мощность излучения лазера; ![]() - чувствительность оптико-акустического детектора);
- чувствительность оптико-акустического детектора);
![]() коэффициент неселективного (фонового) поглощения на длине волны
коэффициент неселективного (фонового) поглощения на длине волны ![]() ;
;
![]() - коэффициент поглощения j-ой газовой компоненты смеси на длине волны
- коэффициент поглощения j-ой газовой компоненты смеси на длине волны ![]() ;
;
![]() - концентрация j-ой газовой компоненты смеси;
- концентрация j-ой газовой компоненты смеси;
М – число спектральных каналов.
Неизвестными величинами в системе уравнений (1) являются ![]() и
и ![]() .
.
В матричной форме уравнение (1) имеет следующий вид (см., например, [5]):
![]() , (2)
, (2)
где:
![]() - M-мерный вектор показателей неселективного поглощения;
- M-мерный вектор показателей неселективного поглощения;
![]() - матрица коэффициентов поглощения газов размерностью
- матрица коэффициентов поглощения газов размерностью ![]() ;
;
![]() - M/2-мерный вектор концентраций газов;
- M/2-мерный вектор концентраций газов;
![]() - M-мерный вектор измеряемых сигналов (показателей поглощения исследуемой смеси).
- M-мерный вектор измеряемых сигналов (показателей поглощения исследуемой смеси).
Коэффициенты ![]() слабо зависят от длины волны. Поэтому обычно спектральные каналы измерения выбирают попарно (для каждого газового компонента) достаточно близко, так что для них коэффициенты
слабо зависят от длины волны. Поэтому обычно спектральные каналы измерения выбирают попарно (для каждого газового компонента) достаточно близко, так что для них коэффициенты ![]() можно положить равными константе. В этом случае из М спектральных каналов, необходимых для контроля газовой смеси, информация М/2 каналов требуется для определения концентраций газов, а информация других М/2 каналов - для определения показателей
можно положить равными константе. В этом случае из М спектральных каналов, необходимых для контроля газовой смеси, информация М/2 каналов требуется для определения концентраций газов, а информация других М/2 каналов - для определения показателей ![]() . В этом случае уравнение (2) лазерного газоанализа преобразуется к виду:
. В этом случае уравнение (2) лазерного газоанализа преобразуется к виду:
![]() , (3)
, (3)
где:
![]() - матрица системы (1) размерностью
- матрица системы (1) размерностью ![]() ;
;
![]() - M-мерный искомый вектор (M/2 компонент этого вектора соответствуют концентрациям газов, другие M/2 компонент - показателям неселективного поглощения).
- M-мерный искомый вектор (M/2 компонент этого вектора соответствуют концентрациям газов, другие M/2 компонент - показателям неселективного поглощения).
Решение уравнения (3) имеет вид:
![]() . (4)
. (4)
При реальных измерениях правая часть уравнения (3) всегда известна со случайной ошибкой. Таким образом, в (2) и (3) вместо ![]() имеем:
имеем:
![]() , (5)
, (5)
где:
![]() - М –мерный вектор шума измерения.
- М –мерный вектор шума измерения.
Случайные ошибки данных измерений приводят (при нахождении решения (4)) к вариациям искомых величин. Эти вариации могут быть очень велики при большом числе обусловленности матрицы ![]() . Такая ситуация характерна для многокомпонентных смесей (с числом компонент обычно более пяти, шести). Выходом из этой ситуации является использование специальных процедур обработки, позволяющих получить приемлемое, физически разумное решение.
. Такая ситуация характерна для многокомпонентных смесей (с числом компонент обычно более пяти, шести). Выходом из этой ситуации является использование специальных процедур обработки, позволяющих получить приемлемое, физически разумное решение.
В практических задачах возникают также ситуации, когда не только приближенные исходные данные, но и сама матрица ![]() известна не точно (в задаче газоанализа это соответствует, например, случаю, когда коэффициенты поглощения исследуемых газов известны с ошибками). Случайные ошибки в матрице коэффициентов поглощения (так же как и шум измерения) приводят (при нахождении решения (4)) к вариациям искомых величин.
известна не точно (в задаче газоанализа это соответствует, например, случаю, когда коэффициенты поглощения исследуемых газов известны с ошибками). Случайные ошибки в матрице коэффициентов поглощения (так же как и шум измерения) приводят (при нахождении решения (4)) к вариациям искомых величин.
Проекционный метод. Статья посвящена исследованию работы проекционного метода [11,12] в задаче многокомпонентного лазерного газоанализа в случае, когда коэффициенты поглощения исследуемых газов известны с ошибками.
Исходным является уравнение (3), которое в другой форме записи имеет вид:
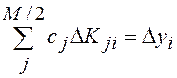 ,
, ![]() . (6)
. (6)
Величина ![]() является вектором в М/2 -мерном пространстве, а каждое из М/2 уравнений в (4) рассматривается как гиперплоскость.
является вектором в М/2 -мерном пространстве, а каждое из М/2 уравнений в (4) рассматривается как гиперплоскость.
Выберем для вектора концентраций газов ![]() начальное приближение -
начальное приближение - ![]() . Следующее приближение
. Следующее приближение ![]() находится как проекция
находится как проекция ![]() на первую гиперплоскость [10,11]:
на первую гиперплоскость [10,11]:
![]() , (7)
, (7)
где: ![]() ; точкой обозначено скалярное произведение векторов.
; точкой обозначено скалярное произведение векторов.
Затем вычисляется проекция ![]() , используя формулу (7), векторы
, используя формулу (7), векторы ![]() и
и ![]() .
.
Далее вычисляется проекция ![]() и т.д. до проекции вычисляется проекция
и т.д. до проекции вычисляется проекция ![]() . На этом первый цикл итераций заканчивается.
. На этом первый цикл итераций заканчивается.
Далее проводится второй цикл итераций, который начинается с вектора ![]() и заканчивается вектором
и заканчивается вектором ![]() . После mитераций получим в качестве решения вектор
. После mитераций получим в качестве решения вектор ![]() .
.
Для задачи лазерного газоанализа многокомпонентных газовых смесей в качестве априорной информации может быть использовано среднее значение концентраций газов в качестве начального приближения ![]() . Данные о средних концентрациях газов вполне доступны во многих задачах контроля состава газовых смесей, например, при рутинном газоанализе.
. Данные о средних концентрациях газов вполне доступны во многих задачах контроля состава газовых смесей, например, при рутинном газоанализе.
Математическое моделирование. Для проверки работоспособности описанного проекционного метода в задаче многокомпонентного лазерного газоанализа было проведено математическое моделирование. При математическом моделировании определялись среднеквадратические ошибки по 1000 реализациям шума измерения и использовалось 20 циклов итераций. Шум моделировался случайным процессом с нормальным законом распределения, нулевым средним значением и заданной дисперсией.
В качестве начального приближения ![]() использовался вектор с нулевыми концентрациями газов и вектор со средними значениями концентраций газов, при этом действительные (заданные при моделировании) значения концентраций газов отличаются от средних значений концентраций газов в большую или меньшую сторону на 50 %. (величину порядка возможных среднеквадратичных отклонений концентраций).
использовался вектор с нулевыми концентрациями газов и вектор со средними значениями концентраций газов, при этом действительные (заданные при моделировании) значения концентраций газов отличаются от средних значений концентраций газов в большую или меньшую сторону на 50 %. (величину порядка возможных среднеквадратичных отклонений концентраций).
Примеры результатов математического моделирования приведены на рисунках 1-6 для для шестикомпонентной смеси (этилен-фреон-12-гидразин-аммиак-метанол-этилакрилат).
На каждом рисунке показаны погрешности ![]() (в процентах) определения концентрации одной из газовых компонент смесей. На рисунках 1, 4 - гидразина; на рисунках 2, 5 – фреона 12; на рисунках 3, 6 - этилена. На всех рисунках ряд 1 – метод прямого решения (4) уравнения лазерного газоанализа; ряд 2 – проекционный метод, для которого в качестве начального приближения взят вектор со средними значениями концентраций газов (заданные значения концентраций газов отличаются от средних значений концентраций газов в большую или меньшую сторону на 50 %). Ошибки
(в процентах) определения концентрации одной из газовых компонент смесей. На рисунках 1, 4 - гидразина; на рисунках 2, 5 – фреона 12; на рисунках 3, 6 - этилена. На всех рисунках ряд 1 – метод прямого решения (4) уравнения лазерного газоанализа; ряд 2 – проекционный метод, для которого в качестве начального приближения взят вектор со средними значениями концентраций газов (заданные значения концентраций газов отличаются от средних значений концентраций газов в большую или меньшую сторону на 50 %). Ошибки ![]() определялись как модуль разности между найденным и действительным значением концентрации, деленный на действительное значение.
определялись как модуль разности между найденным и действительным значением концентрации, деленный на действительное значение.
На рисунках 1-3 погрешности ![]() показаны в зависимости от относительного среднеквадратического значения шума измерения: а – 0,5 %; б – 2, %; в – 5 %; г – 7,5 %; д – 10 %. Для рисунков 1-3 в матрице
показаны в зависимости от относительного среднеквадратического значения шума измерения: а – 0,5 %; б – 2, %; в – 5 %; г – 7,5 %; д – 10 %. Для рисунков 1-3 в матрице ![]() коэффициентов поглощения газов (которая использовалась для восстановления по данным лазерных измерений концентраций газовых компонент смеси) было введено искажение: коэффициент
коэффициентов поглощения газов (которая использовалась для восстановления по данным лазерных измерений концентраций газовых компонент смеси) было введено искажение: коэффициент ![]() был уменьшен в два раза (вместо
был уменьшен в два раза (вместо ![]() в матрице стоял коэффициент 0,5
в матрице стоял коэффициент 0,5![]() ).
).
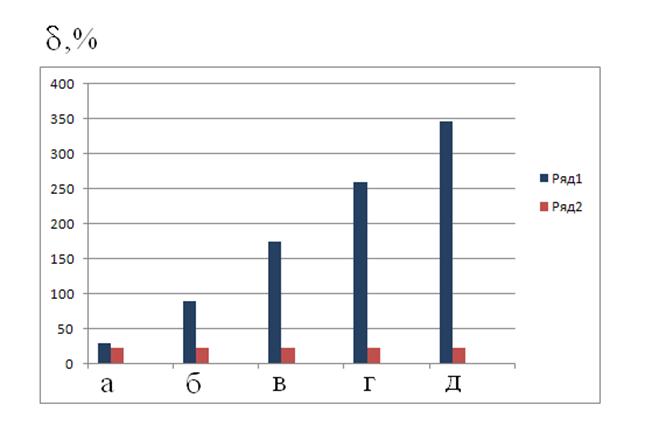
Рис. 1. Зависимость погрешности определения концентрации гидразина от относительного среднеквадратического значения шума измерения

Рис. 2. Зависимость погрешности определения концентрации фреона 12 от относительного среднеквадратического значения шума измерения

Рис. 3. Зависимость погрешности определения концентрации этилена от относительного среднеквадратического значения шума измерения
Из рисунков 1-3 хорошо видно, что для метода прямого решения (4) уравнения лазерного газоанализа с увеличением шума измерения (от 0,5 % до 10 %) погрешности определения концентрации газов возрастают (почти на порядок), достигая у некоторых газовых компонент (гидразин, фреон 12) неприемлемо больших величин – больше 100 % (т.е. концентрация газов в этом случае не определяется).
Для проекционного метода ситуация совершенно другая - с увеличением шума измерения погрешности определения концентрации газов либо практически не меняются или меняются слабо (оставаясь на приемлемом уровне – рис. 1, 2), либо в случае сильного изменения (рис. 3) остаются небольшими.
На рисунках 4-6 погрешности ![]() показаны в зависимости от степени искажения матрицы
показаны в зависимости от степени искажения матрицы ![]() коэффициентов поглощения газов.
коэффициентов поглощения газов.

Рис. 4. Зависимость погрешности определения концентрации гидразина от степени искажения матрицы коэффициентов поглощения газов

Рис. 5. Зависимость погрешности определения концентрации фреона 12 от степени искажения матрицы коэффициентов поглощения газов
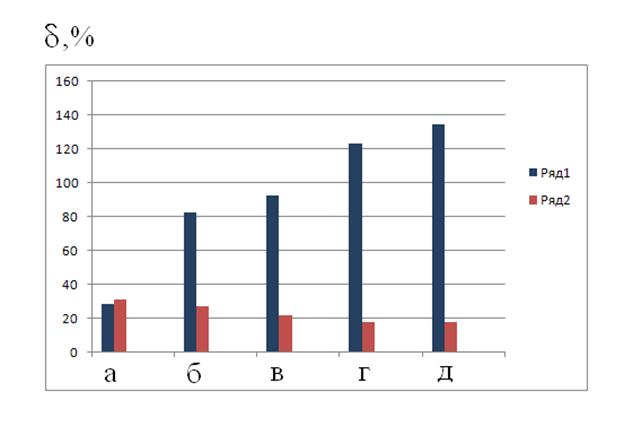
Рис. 6. Зависимость погрешности определения концентрации этилена от степени искажения матрицы коэффициентов поглощения газов
На рисунках 4-6 вместо ![]() в матрице коэффициентов поглощения газовых компонент стоял коэффициент: а – 0,9
в матрице коэффициентов поглощения газовых компонент стоял коэффициент: а – 0,9![]() ; б – 0,7
; б – 0,7![]() ; в – 0,4
; в – 0,4![]() ; г – 0,1
; г – 0,1![]() ; д – 0,01
; д – 0,01![]() . Для рисунков 4-6 относительное среднеквадратическое значение шума измерения полагалось равным 2,5 %.
. Для рисунков 4-6 относительное среднеквадратическое значение шума измерения полагалось равным 2,5 %.
Из рисунков 4-6 хорошо видно, что для метода прямого решения (4) уравнения лазерного газоанализа с увеличением степени искажения матрицы коэффициентов поглощения газов погрешности определения концентрации газов сильно возрастают и становятся неприемлемо большими для всех газов.
Для проекционного метода с увеличением степени искажения матрицы коэффициентов поглощения погрешности определения концентрации газов практически не меняются (даже несколько уменьшаются).
Заключение. Таким образом, в статье описаны процедуры обработки сигналов для лазерного газоанализа многокомпонентных смесей при неточно известной матрице коэффициентов поглощения газовых компонент. Показано, что использование проекционного метода обеспечивает достаточно низкий (в подавляющем большинстве случает не более 30 %) уровень погрешностей определения концентраций газов для многокомпонентных смесей даже при значительном шуме измерения (до 10 %).
Список цитированных источников
1. Межерис Р. Лазерное дистанционное зондирование. М.: Мир,1987. 550 с.
2. Пономарев Ю.Н. Лазерная оптико-акустическая спектроскопия атмосферы // Оптика атмосферы и океана. 1995. Т.8. N1-2. С. 224-241.
3. Лазерная оптико-акустическая спектроскопия межмолекулярных взаимодействий в газах / Ю.Н. Пономарев, Б.Г. Агеев, М.В. Зигрист, В.А. Капитанов, Д. Куртуа, О.Ю. Никифорова. Томск: МГП «РАСКО», 2000. 200 с.
4. Оптико-электронные системы экологического мониторинга природной среды / В.И. Козинцев, В.М. Орлов, М.Л. Белов, В.А. Городничев, Б.В. Стрелков. М.: Изд-во МГТУ им. Н. Э. Баумана, 2002. 528 с.
5. Лазерный оптико-акустический анализ многокомпонентных газовых смесей / В.И. Козинцев, М.Л. Белов, В.А. Городничев, Ю.В. Федотов. М.: Изд-во МГТУ им. Н. Э. Баумана, 2003. 352 с.
6. Основы количественного лазерного анализа / В.И. Козинцев, М.Л. Белов, В.А. Городничев, Ю.В. Федотов. М.: Изд-во МГТУ им. Н. Э. Баумана, 2006. 464 с.
7. Воскобойников Ю.Э., Преображенский Н.Г., Седельников А.Н. Математическая обработка эксперимента в молекулярной газодинамике. Новосибирск: Наука, 1984, 238 с.
8. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979, 288 с.
9. Еременко Л.Н., Козинцев В.И., Городничев В.А. Метод байесовских оценок в задаче лазерного газоанализа // Известия вузов. Физика. 2008. N9. С. 29-35.
10. Лазерный оптико-акустический анализ многокомпонентных газовых смесей / М.Л. Белов,. А.Ю. Бусаргин, В.А. Городничев, Л.Н. Еременко // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2012, № 6. Режим доступа: http://technomag.edu.ru/doc/368798.html (дата обращения 20.06.2012).
11. Преображенский Н.Г., Пикалов В.В. Неустойчивые задачи диагностики плазмы. Новосибирск: Наука, 1982. 238 с.
12. HuangT.S., Barker D.A., Berger S.P. Iterative Image Restoration // Applied Optics. 1975. V.14. N 5, P. 1165-1168.
Публикации с ключевыми словами: лазер, газоанализ, многокомпонентные газовые смеси, проекционный метод
Публикации со словами: лазер, газоанализ, многокомпонентные газовые смеси, проекционный метод
Смотри также:
- Лазерный анализ многокомпонентных смесей газов с сильно отличающимися концентрациями
- Робастный метод определения количественного состава многокомпонентных стационарных газовых смесей
- Сравнительный анализ устойчивых к выбросам сигнала методов определения количественного состава многокомпонентных газовых смесей
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



